4.1平方根同步练习(含解析) 苏科版数学八年级上册
文档属性
| 名称 | 4.1平方根同步练习(含解析) 苏科版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 905.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-15 07:30:33 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
4.1平方根
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若,则的值为( )
A.0 B.1 C. D.
2.已知实数,满足,则代数式的值为( )
A. B. C. D.
3.在实数,2016,,四个数中,是无理数的是( )
A. B.2016 C. D.
4.下列说法不正确的是( )
A.3是9的一个平方根 B.3是9的算术平方根
C.9的平方根是3 D.9的平方根是
5.如图是用4个相同的长方形与1个正方形镶嵌而成的正方形图案.已知该图案的总面积为m,小正方形的面积为n.若用x、y表示长方形的两边长(),请观察图案,指出下列关系式:①、②、③、④若,则.这四个结论中正确的有( )个
A.1个 B.2个 C.3个 D.4个
6.已知,则的值是( )
A.1 B. C.2023 D.
7.在,,,0,这四个数中,为无理数的是( )
A. B. C. D.
8.的相反数是( )
A.2022 B. C. D.
9.下列四个实数中,是无理数的是( )
A.﹣π B.3.1415 C. D.
10.下列运算正确的是( )
A. B. C. D.
11.的算术平方根是( )
A.不存在 B. C.6 D.36
12.下列各数中是无理数的是( )
A.3.14159 B. C. D.
二、填空题
13.若,则xy = .
14.已知m的平方根是2a-9和5a-12,则m的值是 .
15.已知实数满足,则的值为 .
16.的平方根为 ;的算术平方根是 .
17.若,则的值为 .
三、解答题
18.计算:.
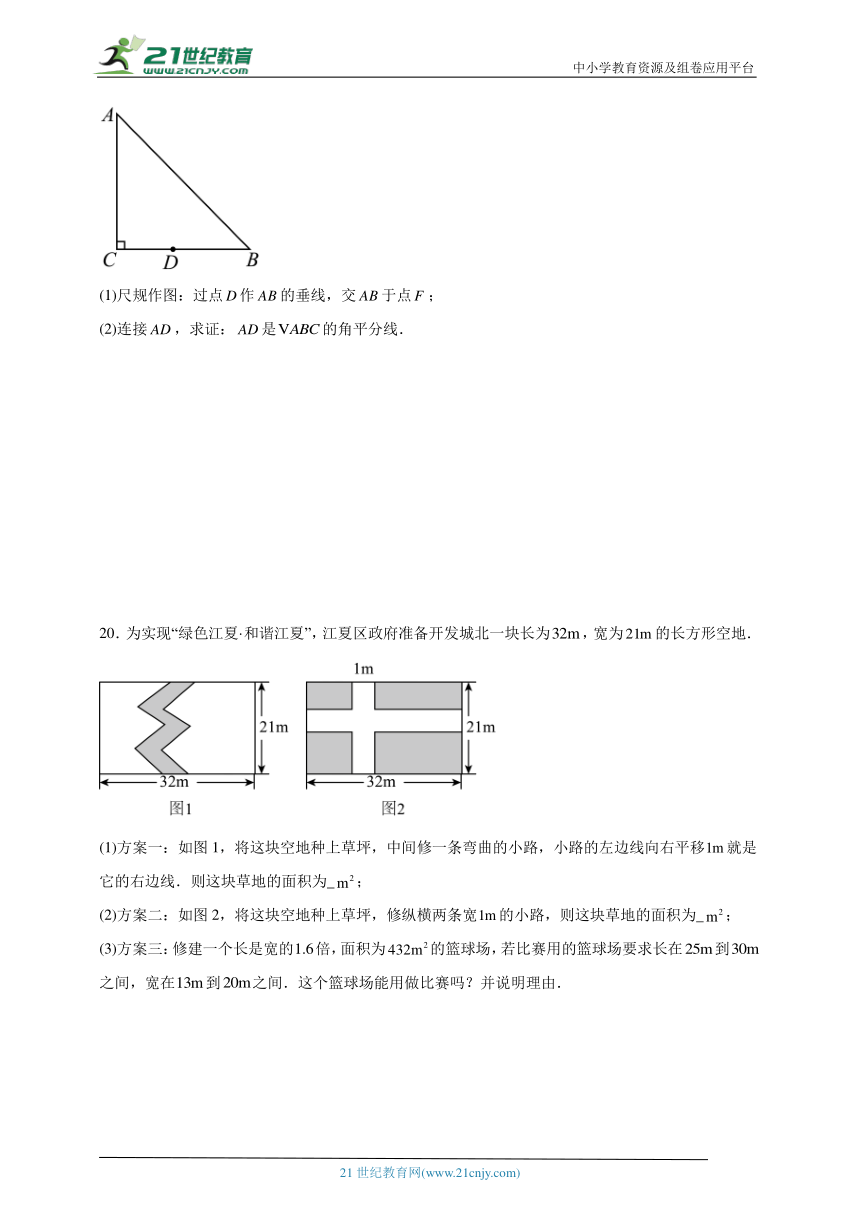
19.如图,在中,,,是上的一点,且,.
(1)尺规作图:过点作的垂线,交于点;
(2)连接,求证:是的角平分线.
20.为实现“绿色江夏·和谐江夏”,江夏区政府准备开发城北一块长为,宽为的长方形空地.
(1)方案一:如图1,将这块空地种上草坪,中间修一条弯曲的小路,小路的左边线向右平移就是它的右边线.则这块草地的面积为 ;
(2)方案二:如图2,将这块空地种上草坪,修纵横两条宽的小路,则这块草地的面积为 ;
(3)方案三:修建一个长是宽的倍,面积为的篮球场,若比赛用的篮球场要求长在到之间,宽在到之间.这个篮球场能用做比赛吗?并说明理由.
21.小明手中有块长方形的硬纸片,如果长减少,宽增加,就成为一个正方形,并且这两个图形的面积相等.
(1)求这个长方形的长、宽各是多少?
(2)现小明想用这块长方形的硬纸片,沿着边的方向裁出一块长与宽的比为,面积为的新长方形纸片,试判断小明能否成功,并说明理由.
22.如图,是一块长方形空地,小刚的爸爸按照图中的方式在空地上用栅栏围出两块面积分别为和的正方形区域ABCD和CEFG(AB、AD、BC、CG、CE、EF、FG均为栅栏).
(1)原长方形空地的长为______m,宽为______m;
(2)求围成的两个正方形区域所需栅栏的总长度;
(3)求长方形空地剩余部分(即阴影部分)的面积.
23.如图,中,,垂足为点D,E为上一点,交于点F,,.
(1)求证:;
(2)如图2,连接,若,,求线段的长.
24.如图,四边形中,的角平分线与的角平分线相交于E点,交于点F,连接,已知,.
(1)求证:;
(2)当,时,求的长度.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C A C C C B C B A D
题号 11 12
答案 C D
1.C
【分析】根据二次根式与绝对值的非负性求出x= 3,y=2,再代值求解即可.
【详解】解:∵且,
∴,解得,
∴,
故选:C.
【点睛】本题考查代数式求值,涉及到二次根式与绝对值的非负性的应用,熟练掌握绝对值和二次根式的性质,准确求出x、y的值是解决问题的关键.
2.A
【分析】根据绝对值和算术平方根的非负性得到且,进而算出x和y的值即可求解.
【详解】解:由题意,由绝对值和算术平方根的非负性可知:
且,
∴,,
∴,
故选:A.
【点睛】本题考查了绝对值和算术平方根的非负性,两个大于等于0的式子相加结果为0,只能是这两个式子分别为0.
3.C
【分析】根据无理数的定义逐一判断即可.
【详解】解:在实数,2016,,四个数中,是无理数的是,
故选:C.
【点睛】本题考查无理数的定义,无理数指的是无限不循环小数.
4.C
【分析】根据平方根的定义、算术平方根的定义分别进行判断,即可得到答案.
【详解】解:3是9的一个平方根,故A正确;
3是9的算术平方根,故B正确;
9的平方根是,故D正确;C错误;
故选:C.
【点睛】本题考查了平方根、算术平方根的定义,解题的关键是掌握所学的定义进行判断.
5.C
【分析】根据该图案的总面积、正方形的面积公式即可判断①;根据小正方形的面积、正方形的面积公式可得,从而可得,再结合①即可判断②;根据四个长方形的面积等于两个正方形的面积之差即可判断③;先将用含的式子表示出来,由此即可判断④.
【详解】解:该图案是正方形,且该图案的总面积为,边长为,
,结论①正确;
小正方形的面积为,边长为,
,
由得:,
则,即,结论②正确;
四个长方形的面积等于两个正方形的面积之差,
,即,结论③正确;
由结论②可知,,
代入得:,
若,则,即,
,结论④错误;
综上,这四个结论中正确的有3个,
故选:C.
【点睛】本题考查了整式的加减与图形面积、算术平方根的应用,读懂图形,熟练掌握各图形面积之间的关系是解题关键.
6.B
【分析】先根据,,,得到,,求出的值,再代入即可求得答案.
【详解】解:,,,
,,
,
,
故选:B.
【点睛】本题主要考查了二次根式的非负性、平方的非负性,根据题意得到,是解题的关键.
7.C
【分析】根据无理数的定义进行判断即可.
【详解】解:根据无理数的定义可知:是无理数,
故选C.
【点睛】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.
8.B
【分析】根据相反数的定义进行求解即可.
【详解】解:的相反数是,故B正确.
故选:B.
【点睛】本题主要考查了相反数的定义,解题的关键是熟练掌握只有符号不同的两个数,互为相反数.
9.A
【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【详解】解:、是无理数,故本选项符合题意;
、3.1415是有限小数,属于有理数,故本选项不合题意;
、是分数,属于有理数,故本选项不合题意;
、是开方开得尽的有理数,故本选项不符合题意.
故选:A.
【点睛】此题主要考查了无理数的定义,解题的关键是:知道初中范围内学习的无理数有:,等;开方开不尽的数;以及像,等有这样规律的数.
10.D
【分析】利用算术平方根的含义与逐一判断即可.
【详解】解:,故A不符合题意;
,故B不符合题意;
没有意义,故C不符合题意;
,故D符合题意;
故选D
【点睛】本题考查的是算术平方根的含义,熟记算术平方根的含义是解本题的关键.
11.C
【详解】试题解析:
36的算术平方根是6.
故选C.
12.D
【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.据此解答即可.
【详解】解:A.3.14159属于有理数,不合题意;
B.属于有理数,符合题意;
C.=5,属于有理数,不合题意;
D.属于无理数,符合题意;
故选:D.
【点睛】本题考查了对无理数定义的应用,能理解无理数的定义是解此题的关键,注意:无理数包括三方面的数:①含π的,②开方开不尽的根式,③一些有规律的数.
13.6
【分析】根据绝对值的非负性,算术平方根的非负性,得出二元一次方程组,解方程组即可求得的值,代入代数式即可求解.
【详解】解:∵,
∴,
解得,
∴,
故答案为:6.
【点睛】本题考查了绝对值的非负性,算术平方根的非负性,解二元一次方程组,求得的值是解题的关键.
14.9
【详解】因为m的平方根是2a-9和5a-12,所以2a-9+5a-12=0,解得:a=3,所以2a-9=-3, m=,故答案为:9.
15.
【分析】此题考查了算术平方根的非负性和绝对值的非负性、代数式的值,根据非负数的性质得到,代入求值即可.
【详解】解:∵,
∴,
∴,
∴,
故答案为:.
16.
【分析】根据平方根和算术平方根的定义即可解答.
【详解】解:,9的平方根为
的平方根为:
,的算术平方根为
的算术平方根为.
故答案为:,.
【点睛】本题考查了求平方根和算术平方根,掌握平方根和算术平方根的定义是解答本题的关键.
17.
【分析】根据题意利用完全平方公式变形得出,,然后求解即可.
【详解】解:∵,
∴,
∴a>0,
∴,
∴,
∴,
∴,
故答案为:.
【点睛】题目主要考查完全平方公式的变形计算,平方根的求法等,熟练掌握运算法则是解题关键.
18.
【分析】先化简绝对值、零次幂、算术平方根、乘方,再运算加减法,即可作答.本题考查了化简绝对值,零次幂、算术平方根、乘方,正确掌握相关性质内容是解题的关键.
【详解】解:
.
19.(1)见解析
(2)见解析
【分析】(1)根据过直线外一点作已知直线的垂线的基本作法画图;
(2)先求出的长,再根据角平分线的判定定理证明.
【详解】(1)解:如下图,直线即为所求.
(2)证明:连接,如图所示.
,,
.
,
,
,
.
设,
在中,,
即,解得.
.
,
又,,
平分.
是的角平分线.
【点睛】本题考查了尺规作图作垂线,角平分线的判定,等腰三角形的判定与性质,勾股定理,熟练掌握相关知识是解题的关键.
20.(1)
(2)
(3)这个篮球场能用做比赛,理由见解析
【分析】本题考查了平移的性质,有理数的混合运算的应用,利用平方根解方程等知识.熟练掌握平移的性质,有理数的混合运算的应用,利用平方根解方程是解题的关键.
(1)由平移可知,小路的面积为,根据草地的面积为,计算求解即可;
(2)由题意知,草地的面积为,计算求解即可;
(3)设宽为,则长为,依题意得,,可求,根据,可知宽满足要求;由,,可知长满足要求;然后作答即可.
【详解】(1)解:由平移可知,小路的面积为,
∴草地的面积为,
故答案为:;
(2)解:由题意知,草地的面积为,
故答案为:;
(3)解:这个篮球场能用做比赛,理由如下;
设宽为,则长为,
依题意得,,
解得,,
∵,
∴宽满足要求;
∵,,
∴长满足要求;
∴这个篮球场能用做比赛.
21.(1)这个长方形的长、宽分别是,
(2)小明不能成功,见解析
【分析】本题考查了二元一次方程组的实际应用:
(1)根据长方形、正方形的概念以及面积公式列出方程组,解方程组即可;
(2)根据长方形的面积公式列出方程,根据实际情况判断即可.
【详解】(1)解:设长方形的长为,宽为,
则,解得,,
答:这个长方形的长、宽分别是,;
(2)解:小明不能成功.
理由:设裁出的长为,宽为,
则,解之得,,
裁出的长为,宽为,
21和18都大于16,
小明不能成功.
22.(1)16,9
(2)围成的两个正方形区域所需栅栏的总长度为57m
(3)长方形空地剩余部分(即阴影部分)的面积为
【分析】本题考查算术平方根的应用,熟练掌握算术平方根的化简和运算是解题的关键.
(1)由正方形的面积可得边长分别为,,再利用算术平方根的性质化简,即可求解;
(2)根据题意求围成的两个正方形区域所需栅栏的总长度,即可求解;
(3)先求出阴影部分的长和宽,再求其面积即可.
【详解】(1)根据题意得:正方形的边长分别为,正方形的边长分别为,
,
故答案为:16,9;
(2)根据题意得:围成的两个正方形区域所需栅栏的总长度为:;
(3)根据题意得:,
长方形空地剩余部分(即阴影部分)的面积为
23.(1)见解析
(2)
【分析】本题考查了全等三角形的判定和性质,三角形面积,掌握全等三角形的性质是解题关键.
(1)利用“”证明即可;
(2)由三角形面积比可得,由(1)可知,,得出,再结合三角形面积公式,求出,即可得出的长.
【详解】(1)证明:,
,
在和中,
,
;
(2)解:,
,
,
由(1)可知,,
,
,
,
,
,,
.
24.(1)见解析
(2)4
【分析】本题考查角平分线的定义、平行线的判定与性质、等腰三角形的判定、三角形的内角和定理、勾股定理等知识,熟练掌握平行线的判定与性质,证明是解答的关键.
(1)根据角平分线的定义求得,,则,然后根据平行线的判定可证得结论;
(2)根据平行线的性质和等角对等边证得,再利用三角形的内角和定理求得,在中,利用勾股定理求解即可.
【详解】(1)解:∵的角平分线与的角平分线相交于E点,
∴,,
∵,,
∴,,
∴,
∴;
(2)解:∵,
∴,又,
∴,
∴,
又,
∴,
在中,,,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.1平方根
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若,则的值为( )
A.0 B.1 C. D.
2.已知实数,满足,则代数式的值为( )
A. B. C. D.
3.在实数,2016,,四个数中,是无理数的是( )
A. B.2016 C. D.
4.下列说法不正确的是( )
A.3是9的一个平方根 B.3是9的算术平方根
C.9的平方根是3 D.9的平方根是
5.如图是用4个相同的长方形与1个正方形镶嵌而成的正方形图案.已知该图案的总面积为m,小正方形的面积为n.若用x、y表示长方形的两边长(),请观察图案,指出下列关系式:①、②、③、④若,则.这四个结论中正确的有( )个
A.1个 B.2个 C.3个 D.4个
6.已知,则的值是( )
A.1 B. C.2023 D.
7.在,,,0,这四个数中,为无理数的是( )
A. B. C. D.
8.的相反数是( )
A.2022 B. C. D.
9.下列四个实数中,是无理数的是( )
A.﹣π B.3.1415 C. D.
10.下列运算正确的是( )
A. B. C. D.
11.的算术平方根是( )
A.不存在 B. C.6 D.36
12.下列各数中是无理数的是( )
A.3.14159 B. C. D.
二、填空题
13.若,则xy = .
14.已知m的平方根是2a-9和5a-12,则m的值是 .
15.已知实数满足,则的值为 .
16.的平方根为 ;的算术平方根是 .
17.若,则的值为 .
三、解答题
18.计算:.
19.如图,在中,,,是上的一点,且,.
(1)尺规作图:过点作的垂线,交于点;
(2)连接,求证:是的角平分线.
20.为实现“绿色江夏·和谐江夏”,江夏区政府准备开发城北一块长为,宽为的长方形空地.
(1)方案一:如图1,将这块空地种上草坪,中间修一条弯曲的小路,小路的左边线向右平移就是它的右边线.则这块草地的面积为 ;
(2)方案二:如图2,将这块空地种上草坪,修纵横两条宽的小路,则这块草地的面积为 ;
(3)方案三:修建一个长是宽的倍,面积为的篮球场,若比赛用的篮球场要求长在到之间,宽在到之间.这个篮球场能用做比赛吗?并说明理由.
21.小明手中有块长方形的硬纸片,如果长减少,宽增加,就成为一个正方形,并且这两个图形的面积相等.
(1)求这个长方形的长、宽各是多少?
(2)现小明想用这块长方形的硬纸片,沿着边的方向裁出一块长与宽的比为,面积为的新长方形纸片,试判断小明能否成功,并说明理由.
22.如图,是一块长方形空地,小刚的爸爸按照图中的方式在空地上用栅栏围出两块面积分别为和的正方形区域ABCD和CEFG(AB、AD、BC、CG、CE、EF、FG均为栅栏).
(1)原长方形空地的长为______m,宽为______m;
(2)求围成的两个正方形区域所需栅栏的总长度;
(3)求长方形空地剩余部分(即阴影部分)的面积.
23.如图,中,,垂足为点D,E为上一点,交于点F,,.
(1)求证:;
(2)如图2,连接,若,,求线段的长.
24.如图,四边形中,的角平分线与的角平分线相交于E点,交于点F,连接,已知,.
(1)求证:;
(2)当,时,求的长度.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C A C C C B C B A D
题号 11 12
答案 C D
1.C
【分析】根据二次根式与绝对值的非负性求出x= 3,y=2,再代值求解即可.
【详解】解:∵且,
∴,解得,
∴,
故选:C.
【点睛】本题考查代数式求值,涉及到二次根式与绝对值的非负性的应用,熟练掌握绝对值和二次根式的性质,准确求出x、y的值是解决问题的关键.
2.A
【分析】根据绝对值和算术平方根的非负性得到且,进而算出x和y的值即可求解.
【详解】解:由题意,由绝对值和算术平方根的非负性可知:
且,
∴,,
∴,
故选:A.
【点睛】本题考查了绝对值和算术平方根的非负性,两个大于等于0的式子相加结果为0,只能是这两个式子分别为0.
3.C
【分析】根据无理数的定义逐一判断即可.
【详解】解:在实数,2016,,四个数中,是无理数的是,
故选:C.
【点睛】本题考查无理数的定义,无理数指的是无限不循环小数.
4.C
【分析】根据平方根的定义、算术平方根的定义分别进行判断,即可得到答案.
【详解】解:3是9的一个平方根,故A正确;
3是9的算术平方根,故B正确;
9的平方根是,故D正确;C错误;
故选:C.
【点睛】本题考查了平方根、算术平方根的定义,解题的关键是掌握所学的定义进行判断.
5.C
【分析】根据该图案的总面积、正方形的面积公式即可判断①;根据小正方形的面积、正方形的面积公式可得,从而可得,再结合①即可判断②;根据四个长方形的面积等于两个正方形的面积之差即可判断③;先将用含的式子表示出来,由此即可判断④.
【详解】解:该图案是正方形,且该图案的总面积为,边长为,
,结论①正确;
小正方形的面积为,边长为,
,
由得:,
则,即,结论②正确;
四个长方形的面积等于两个正方形的面积之差,
,即,结论③正确;
由结论②可知,,
代入得:,
若,则,即,
,结论④错误;
综上,这四个结论中正确的有3个,
故选:C.
【点睛】本题考查了整式的加减与图形面积、算术平方根的应用,读懂图形,熟练掌握各图形面积之间的关系是解题关键.
6.B
【分析】先根据,,,得到,,求出的值,再代入即可求得答案.
【详解】解:,,,
,,
,
,
故选:B.
【点睛】本题主要考查了二次根式的非负性、平方的非负性,根据题意得到,是解题的关键.
7.C
【分析】根据无理数的定义进行判断即可.
【详解】解:根据无理数的定义可知:是无理数,
故选C.
【点睛】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.
8.B
【分析】根据相反数的定义进行求解即可.
【详解】解:的相反数是,故B正确.
故选:B.
【点睛】本题主要考查了相反数的定义,解题的关键是熟练掌握只有符号不同的两个数,互为相反数.
9.A
【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【详解】解:、是无理数,故本选项符合题意;
、3.1415是有限小数,属于有理数,故本选项不合题意;
、是分数,属于有理数,故本选项不合题意;
、是开方开得尽的有理数,故本选项不符合题意.
故选:A.
【点睛】此题主要考查了无理数的定义,解题的关键是:知道初中范围内学习的无理数有:,等;开方开不尽的数;以及像,等有这样规律的数.
10.D
【分析】利用算术平方根的含义与逐一判断即可.
【详解】解:,故A不符合题意;
,故B不符合题意;
没有意义,故C不符合题意;
,故D符合题意;
故选D
【点睛】本题考查的是算术平方根的含义,熟记算术平方根的含义是解本题的关键.
11.C
【详解】试题解析:
36的算术平方根是6.
故选C.
12.D
【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.据此解答即可.
【详解】解:A.3.14159属于有理数,不合题意;
B.属于有理数,符合题意;
C.=5,属于有理数,不合题意;
D.属于无理数,符合题意;
故选:D.
【点睛】本题考查了对无理数定义的应用,能理解无理数的定义是解此题的关键,注意:无理数包括三方面的数:①含π的,②开方开不尽的根式,③一些有规律的数.
13.6
【分析】根据绝对值的非负性,算术平方根的非负性,得出二元一次方程组,解方程组即可求得的值,代入代数式即可求解.
【详解】解:∵,
∴,
解得,
∴,
故答案为:6.
【点睛】本题考查了绝对值的非负性,算术平方根的非负性,解二元一次方程组,求得的值是解题的关键.
14.9
【详解】因为m的平方根是2a-9和5a-12,所以2a-9+5a-12=0,解得:a=3,所以2a-9=-3, m=,故答案为:9.
15.
【分析】此题考查了算术平方根的非负性和绝对值的非负性、代数式的值,根据非负数的性质得到,代入求值即可.
【详解】解:∵,
∴,
∴,
∴,
故答案为:.
16.
【分析】根据平方根和算术平方根的定义即可解答.
【详解】解:,9的平方根为
的平方根为:
,的算术平方根为
的算术平方根为.
故答案为:,.
【点睛】本题考查了求平方根和算术平方根,掌握平方根和算术平方根的定义是解答本题的关键.
17.
【分析】根据题意利用完全平方公式变形得出,,然后求解即可.
【详解】解:∵,
∴,
∴a>0,
∴,
∴,
∴,
∴,
故答案为:.
【点睛】题目主要考查完全平方公式的变形计算,平方根的求法等,熟练掌握运算法则是解题关键.
18.
【分析】先化简绝对值、零次幂、算术平方根、乘方,再运算加减法,即可作答.本题考查了化简绝对值,零次幂、算术平方根、乘方,正确掌握相关性质内容是解题的关键.
【详解】解:
.
19.(1)见解析
(2)见解析
【分析】(1)根据过直线外一点作已知直线的垂线的基本作法画图;
(2)先求出的长,再根据角平分线的判定定理证明.
【详解】(1)解:如下图,直线即为所求.
(2)证明:连接,如图所示.
,,
.
,
,
,
.
设,
在中,,
即,解得.
.
,
又,,
平分.
是的角平分线.
【点睛】本题考查了尺规作图作垂线,角平分线的判定,等腰三角形的判定与性质,勾股定理,熟练掌握相关知识是解题的关键.
20.(1)
(2)
(3)这个篮球场能用做比赛,理由见解析
【分析】本题考查了平移的性质,有理数的混合运算的应用,利用平方根解方程等知识.熟练掌握平移的性质,有理数的混合运算的应用,利用平方根解方程是解题的关键.
(1)由平移可知,小路的面积为,根据草地的面积为,计算求解即可;
(2)由题意知,草地的面积为,计算求解即可;
(3)设宽为,则长为,依题意得,,可求,根据,可知宽满足要求;由,,可知长满足要求;然后作答即可.
【详解】(1)解:由平移可知,小路的面积为,
∴草地的面积为,
故答案为:;
(2)解:由题意知,草地的面积为,
故答案为:;
(3)解:这个篮球场能用做比赛,理由如下;
设宽为,则长为,
依题意得,,
解得,,
∵,
∴宽满足要求;
∵,,
∴长满足要求;
∴这个篮球场能用做比赛.
21.(1)这个长方形的长、宽分别是,
(2)小明不能成功,见解析
【分析】本题考查了二元一次方程组的实际应用:
(1)根据长方形、正方形的概念以及面积公式列出方程组,解方程组即可;
(2)根据长方形的面积公式列出方程,根据实际情况判断即可.
【详解】(1)解:设长方形的长为,宽为,
则,解得,,
答:这个长方形的长、宽分别是,;
(2)解:小明不能成功.
理由:设裁出的长为,宽为,
则,解之得,,
裁出的长为,宽为,
21和18都大于16,
小明不能成功.
22.(1)16,9
(2)围成的两个正方形区域所需栅栏的总长度为57m
(3)长方形空地剩余部分(即阴影部分)的面积为
【分析】本题考查算术平方根的应用,熟练掌握算术平方根的化简和运算是解题的关键.
(1)由正方形的面积可得边长分别为,,再利用算术平方根的性质化简,即可求解;
(2)根据题意求围成的两个正方形区域所需栅栏的总长度,即可求解;
(3)先求出阴影部分的长和宽,再求其面积即可.
【详解】(1)根据题意得:正方形的边长分别为,正方形的边长分别为,
,
故答案为:16,9;
(2)根据题意得:围成的两个正方形区域所需栅栏的总长度为:;
(3)根据题意得:,
长方形空地剩余部分(即阴影部分)的面积为
23.(1)见解析
(2)
【分析】本题考查了全等三角形的判定和性质,三角形面积,掌握全等三角形的性质是解题关键.
(1)利用“”证明即可;
(2)由三角形面积比可得,由(1)可知,,得出,再结合三角形面积公式,求出,即可得出的长.
【详解】(1)证明:,
,
在和中,
,
;
(2)解:,
,
,
由(1)可知,,
,
,
,
,
,,
.
24.(1)见解析
(2)4
【分析】本题考查角平分线的定义、平行线的判定与性质、等腰三角形的判定、三角形的内角和定理、勾股定理等知识,熟练掌握平行线的判定与性质,证明是解答的关键.
(1)根据角平分线的定义求得,,则,然后根据平行线的判定可证得结论;
(2)根据平行线的性质和等角对等边证得,再利用三角形的内角和定理求得,在中,利用勾股定理求解即可.
【详解】(1)解:∵的角平分线与的角平分线相交于E点,
∴,,
∵,,
∴,,
∴,
∴;
(2)解:∵,
∴,又,
∴,
∴,
又,
∴,
在中,,,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
