3.9弧长及扇形的面积同步练习(含解析) 北师大版数学九年级下册
文档属性
| 名称 | 3.9弧长及扇形的面积同步练习(含解析) 北师大版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-15 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
3.9弧长及扇形的面积
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,已知点C、D在上,直径,弦、相交于点E.若,则阴影部分面积为( )
A. B. C. D.
2.已知圆锥的母线长13,圆锥的高12,则这个圆锥的侧面积是( ).
A. B. C. D.
3.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ABC=120°,则劣弧AC的长为( )
A.2π B.4π C.5π D.6π
4.如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )
A.1 B. C.2 D.
5.用一个半径为3,圆心角为120°的扇形围成一个圆锥,则这个圆锥的底面半径是( )
A.1 B.2 C.π D.2π
6.如图,以为圆心,半径为2的圆与x轴交于A,B两点,与y轴交于C,D两点,点E为上一动点,作于点F.当点E从点B出发,顺时针旋转到点D时,点F所经过的路径长为( )
A. B. C. D.
7.如图,正方形的边长为1,以点O为圆心,为半径作扇形,弧与相交于点,设正方形与扇形之间的阴影部分的面积为;然后以为对角线作正方形,又以点O为圆心,为半径作扇形,弧与相交于点,设正方形与扇形之间的阴影部分面积为;按此规律继续作下去,设正方形与扇形之间的阴影部分面积为,则等于( )
A. B. C. D.
8.若一个圆锥的底面圆的周长是6π,母线长是6,则圆锥的侧面积是( )
A.36π B.18π C.12π D.6π
9.如图,BC为直径,若,,则图中灰色区域的面积为( )
A. B. C. D.
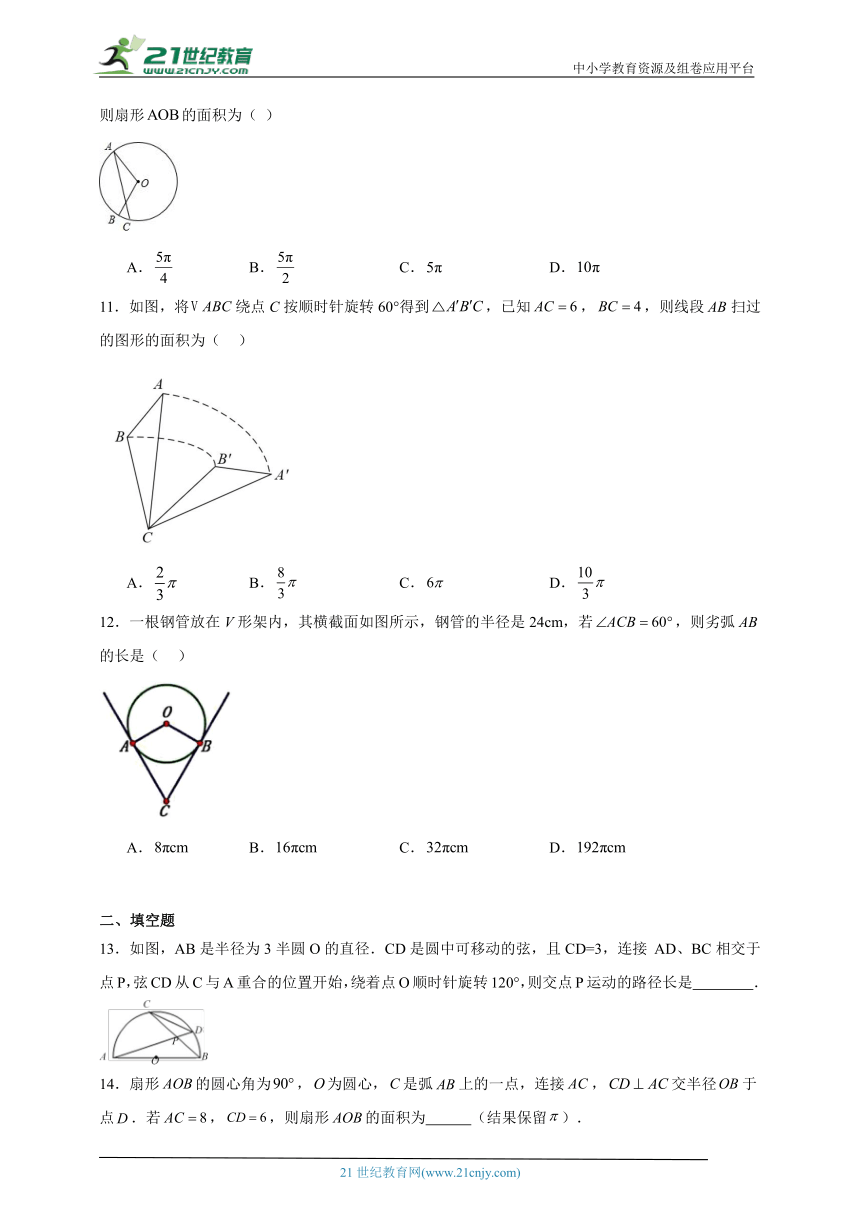
10.如图,已知、、为上三点,连接、、、,若,,则扇形的面积为( )
A. B. C. D.
11.如图,将绕点C按顺时针旋转60°得到,已知,,则线段AB扫过的图形的面积为( )
A. B. C. D.
12.一根钢管放在V形架内,其横截面如图所示,钢管的半径是24cm,若,则劣弧AB的长是( )
A. B. C. D.
二、填空题
13.如图,AB是半径为3半圆O的直径.CD是圆中可移动的弦,且CD=3,连接 AD、BC相交于点P,弦CD从C与A重合的位置开始,绕着点O顺时针旋转120°,则交点P运动的路径长是 .
14.扇形的圆心角为,为圆心,是弧上的一点,连接,交半径于点.若,,则扇形的面积为 (结果保留).
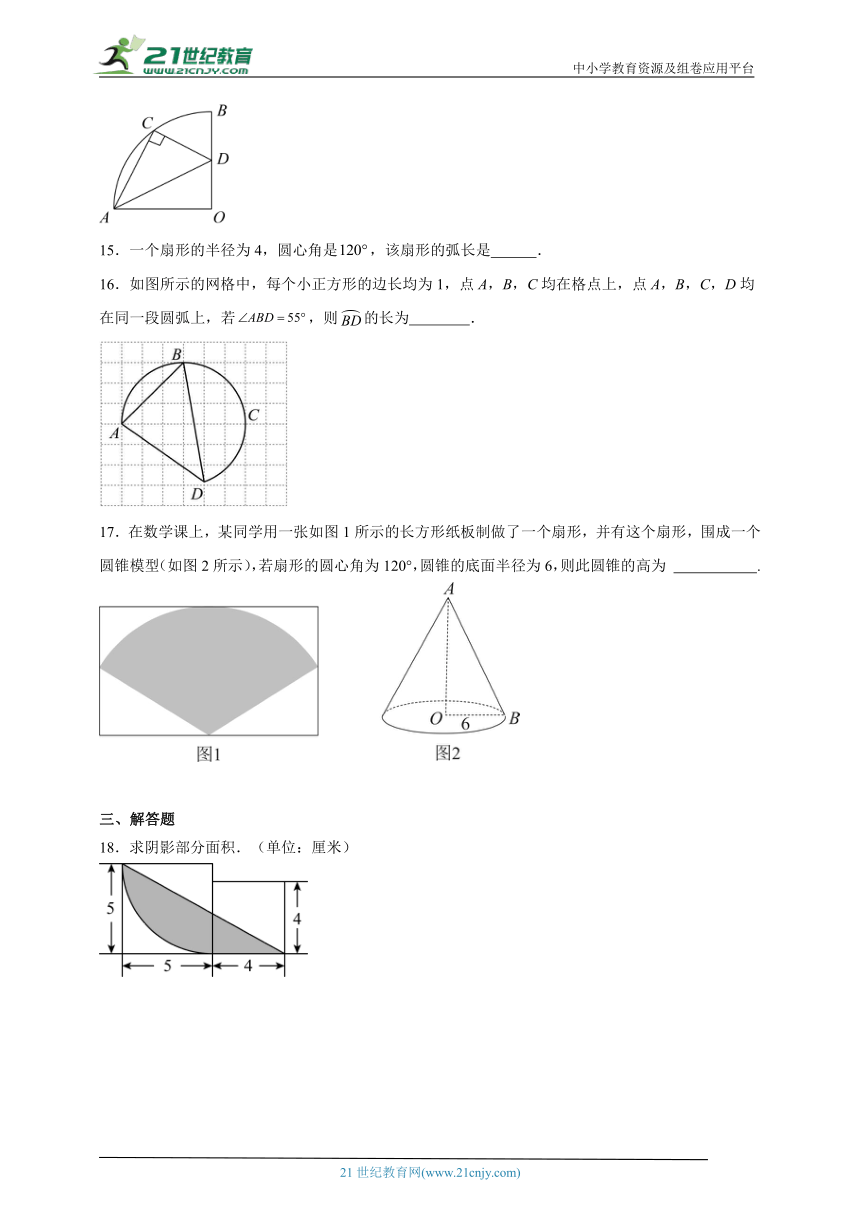
15.一个扇形的半径为4,圆心角是,该扇形的弧长是 .
16.如图所示的网格中,每个小正方形的边长均为1,点A,B,C均在格点上,点A,B,C,D均在同一段圆弧上,若,则的长为 .
17.在数学课上,某同学用一张如图1所示的长方形纸板制做了一个扇形,并有这个扇形,围成一个圆锥模型(如图2所示),若扇形的圆心角为120°,圆锥的底面半径为6,则此圆锥的高为 .
三、解答题
18.求阴影部分面积.(单位:厘米)
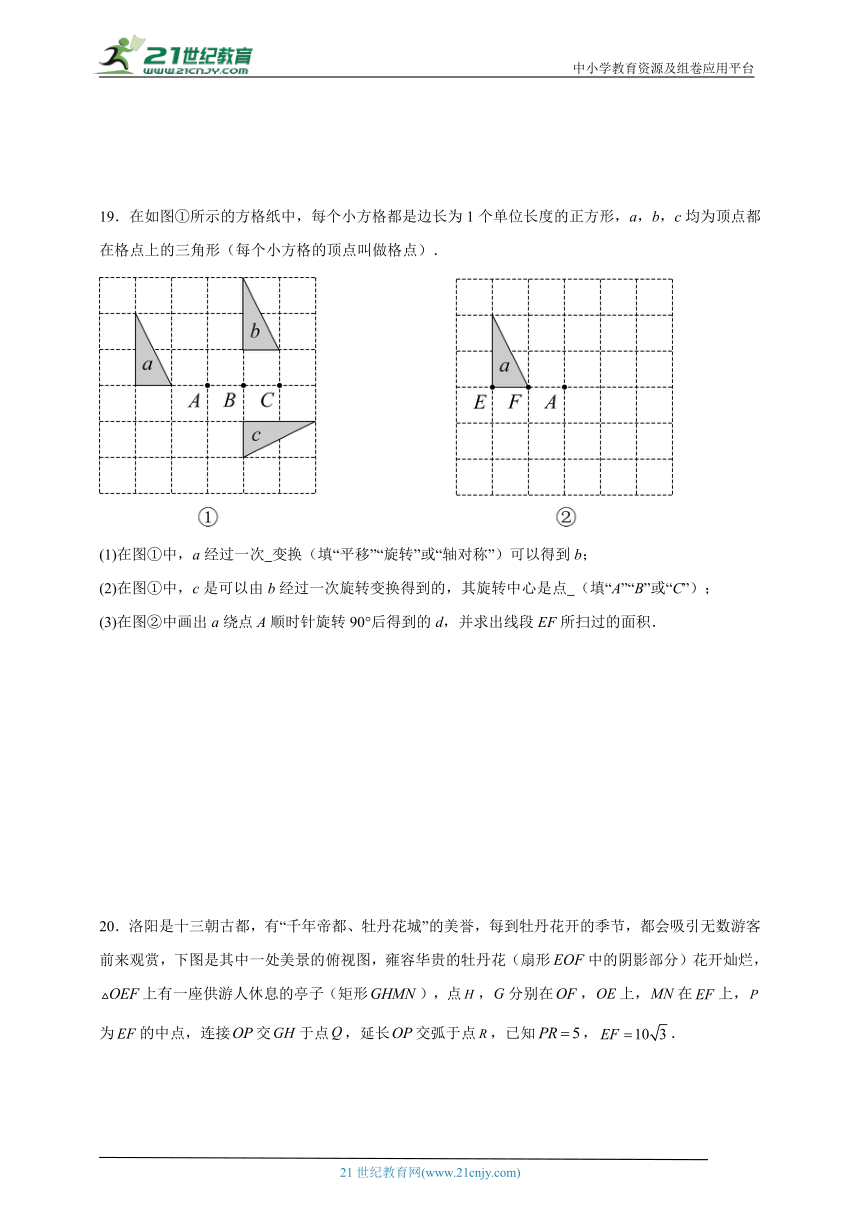
19.在如图①所示的方格纸中,每个小方格都是边长为1个单位长度的正方形,a,b,c均为顶点都在格点上的三角形(每个小方格的顶点叫做格点).
(1)在图①中,a经过一次 变换(填“平移”“旋转”或“轴对称”)可以得到b;
(2)在图①中,c是可以由b经过一次旋转变换得到的,其旋转中心是点 (填“A”“B”或“C”);
(3)在图②中画出a绕点A顺时针旋转90°后得到的d,并求出线段EF所扫过的面积.
20.洛阳是十三朝古都,有“千年帝都、牡丹花城”的美誉,每到牡丹花开的季节,都会吸引无数游客前来观赏,下图是其中一处美景的俯视图,雍容华贵的牡丹花(扇形中的阴影部分)花开灿烂,上有一座供游人休息的亭子(矩形),点,分别在,上,在上,为的中点,连接交于点,延长交弧于点,已知,.
(1)求扇形的半径;
(2)若,求阴影部分的面积.
21.筒车是我国古代利用水力驱动的灌溉工具,如图,半径为的筒车按逆时针方向每分钟转圈,筒车与水面分别交于点A、B,筒车的轴心O距离水面的高度为,筒车上均匀分布着若干个盛水筒,若以某个盛水筒P刚浮出水面(点A)时开始计算时间.
(1)求盛水筒P从A点到达最高点所经过的路程;
(2)求浮出水面秒时,盛水筒P到水面的距离;
(3)若接水槽所在直线是的切线,且与直线交于点M,,直接写出盛水筒P从最高点开始,经过多长时间恰好第一次落在直线上.(参考数据:,,)
22.综合与实践
主题:制作圆锥形生日帽.
素材:一张圆形纸板、装饰彩带.
步骤1:如图1,将一个底面半径为r的圆锥侧面展开,可得到一个半径为l、圆心角为的扇形.制作圆锥形生日帽时,要先确定扇形的圆心角度数,再度量裁剪材料.
步骤2:如图2,把剪好的纸板粘合成圆锥形生日帽.
在制作好的生日帽中,,,C是的中点,现要从点A到点C再到点A之间拉一条装饰彩带,求彩带长度的最小值.
23.如图,点是内一点,,垂足为点,将线段绕点顺时针旋转得到扇形,过点作交于点,连接,与弧交于点,过点作交于点.
(1)求证:;
(2)已知,.
①通过计算比较线段和弧哪个长度更长;
②计算图中阴影部分的面积(结果保留).(参考数据:)
24.如图,在中,为的直径,为的弦,点是的中点,过点作的垂线,交于点,交于点,分别连接.
(1)与的数量关系是_______;
(2)求证:;
(3)若,求阴影部分图形的面积.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B A A B C B C B
题号 11 12
答案 D B
1.B
【分析】本题考查了等腰三角形的性质,圆周角定理和弧之间的关系,扇形的面积等.连接,根据,得出,进而得到,利用即可求解.
【详解】解:连接,
∵是直径,
∴,
∵,
∴,
∴,
∴,
故选:B.
2.B
【分析】可设圆锥底面半径长为,利用勾股定理求出,再根据圆锥侧面展开图的面积,即可求解.
【详解】可设圆锥底面半径长为,
∵,,
由勾股定理得,
圆锥侧面展开图的面积,
所以圆锥的侧面积为.
故选:B.
【点睛】本题考查圆锥的计算,解题的关键是熟练掌握圆锥的侧面积=×底面圆周长×母线长.
3.B
【分析】连接OA、OC,然后根据圆内接四边形的性质及圆周角定理求得∠AOC的度数,最后根据弧长公式求解.
【详解】解:连接OA、OC,
∵∠ABC=120°,
∴∠ADC=60°,
∴∠AOC=2∠ADC=120°,
则劣弧AC的长为:.
故选:B.
【点睛】本题考查了弧长的计算以及圆周角定理、圆内接四边形的性质,解答本题的关键是掌握弧长公式.
4.A
【分析】设AT交⊙O于C,连接BC,如图,利用切线的性质得到∠ABT=90°,则可判断△ABT为等腰直角三角形,再根据圆周角定理得到∠ACB=90°,所以BC=AC=TC,则S弓形AC=S弓形BC,然后利用阴影部分的面积=S△BTC=S△ABT进行计算.
【详解】解:设AT交⊙O于C,连接BC,如图,
∵BT是⊙O的切线,
∴BT⊥AB,
∴∠ABT=90°,
∵∠ATB=45°,
∴△ABT为等腰直角三角形,
∵AB为直径,
∴∠ACB=90°,
∴BC⊥AT,
∴BC=AC=TC,
∴S弓形AC=S弓形BC,
∴阴影部分的面积=S△BTC=S△ABT=××2×2=1.
故选:A.
【点睛】本题考查求不规则图形的面积,解决问题的关键是把不规则图形转化为规则图形,本题是利用割补法把不规则图形转化为规则图形.
5.A
【分析】设该圆锥底面圆的半径为rcm,则可根据圆锥的侧面展开图为扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2πr=,然后解方程即可.
【详解】解:设该圆锥底面圆的半径为r,
根据题意得2πr=,
解得r=1,
即该圆锥底面圆的半径为1.
故选:A.
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
6.B
【分析】连接,,,先由圆周角定理得到点F的运动轨迹是以为直径的圆上,且点O在圆上,进而得到当点E从点B出发,顺时针旋转到点D时,点F所经过的路径长为的长;根据勾股定理和锐角三角函数求得,,则所对的圆心角的度数为,利用弧长公式求得的长即可求解.
【详解】解:连接,,,
∵,
∴,
∴点F的运动轨迹是以为直径的圆上,且点O在圆上,
当点E在点B处时,,点F与O重合;
当点E在点D处时,∵以为圆心,半径为2的圆与x轴交于A,B两点,与y轴交于C,D两点,
∴即,点F与A重合,
∴当点E从点B出发,顺时针旋转到点D时,点F所经过的路径长为的长;
∵,,,
∴,
∵,
∴,,
∴,则所对的圆心角的度数为,
∴的长为,即点F所经过的路径长为,
故选:B.
【点睛】本题考查圆周角定理、解直角三角形、弧长公式、坐标与图形等知识,正确得到点F的运动轨迹以及点F所经过的路径长为的长是解答的关键.
7.C
【分析】分别求出和,找到阴影部分面积的变化规律,即可得到.
【详解】解:正方形的边长为1,
则正方形的面积为1, ,以O为圆心,为半径作扇形,得到,
以为对角线作正方形,又以O为圆心,为半径作扇形,得到,
以此类推得到﹣,
故.
故选:C.
【点睛】此题考查了正方形的性质、扇形面积公式等知识,找到图形面积的规律是解题的关键.
8.B
【分析】根据圆锥侧面面积公式求解即可.
【详解】解:S圆锥侧面积=.
故选择B.
【点睛】本题考查圆锥的侧面积,掌握扇形面积公式是解题关键.
9.C
【分析】由,则∠B+∠C=100°,从而得出∠ODB+∠OEC=100°,根据三角形的内角和定理得∠BOD+∠COE=160°,再由扇形的面积公式得出答案.
【详解】解:如图:
∵∠A=80°,
∴∠B+∠C=100°,
∵BC=6,
∴OB=OC=OD=OE=3,
∴∠ODB+∠OEC=100°,
即(180°∠BOD)+(180°∠COE)=100°,
整理可得:∠BOD+∠COE=160°,
∴图中灰色区域的面积为;
故选:C.
【点睛】本题考查了扇形面积的计算和三角形的内角和定理,是基础知识要熟练掌握.
10.B
【分析】根据圆周角定理你求出∠AOB,带入扇形的面积公式运算即可.
【详解】解:∵∠ACB=50°,
∴∠AOB=2∠ACB=100°,
∴扇形AOB的面积,故选:B.
【点睛】本题考查了圆周角定理求面积公式,熟悉掌握公式是解决本题的关键.
11.D
【分析】根据图形可以得出扫过的图形的面积,由旋转的性质就可以得出,从而得出扫过的图形的面积求出其值即可.
【详解】解:∵绕点C旋转60°得到,
∴,
∴,.
∵扫过的图形的面积,
∴扫过的图形的面积,
∴扫过的图形的面积.
故选:D.
【点睛】本题考查了旋转的性质的运用,全等三角形的性质的运用,扇形的面积公式的运用,解答时根据旋转的性质求解是关键.
12.B
【分析】先利用v形架与圆的关系求出∠C+∠AOB=180°,由∠C=60°,可求∠AOB=120°,由OB=24cm,利用弧长公式求即可.
【详解】解:∵AC与BC是圆的切线,
∴OA⊥AC,OB⊥CB,
∴∠OAC=∠OBC=90°,
∴∠C+∠AOB=360°-∠OAC-∠OBC=360°-90°-90°=180°,
∵∠C=60°,
∴∠AOB=180°-60°=120°,
∵OB=24cm,
∴=cm.
故选择B.
【点睛】本题考查直线与圆的位置关系,四边形内角和,弧长公式,掌握直线与圆的位置关系,四边形内角和,弧长公式是解题关键.
13.
【分析】根据题意找到不变的量可作下图,求得点P的轨迹也是圆,圆心角度数为120度,再根据AB的长求出⊙O’的半径即可求出点P运动的路径长
【详解】连接AC,BD,OC,OD,∵AB是半径为3半圆O的直径
∴CO=DO=CD=3,
∴△COD为等边三角形,
∠COD=60°,
则∠DAC=∠DBC=30°,
又AB为直径得∠APB=180°-∠DAB-∠CBA=120°
由定径对定角,得出P轨迹为圆,
以AB为底作顶角为120°的等腰△ABO’,
∵AB=6,求得AO’=2
故P的运动轨迹为120°的圆弧,
【点睛】此题主要考查圆内综合问题,解题的关键是熟知圆周角定理与弧长公式.
14.
【分析】过作于,交于,则,根据勾股定理和扇形的面积公式即可得到结论.
【详解】解:过作于,交于,
则,
,
,
,
,
,
,
,
,
,
,
,
扇形的面积,
故答案为:.
【点睛】本题考查了扇形面积的计算,勾股定理,垂径定理,直角三角形的性质,正确地作出辅助线是解题的关键.
15.
【分析】本题考查了弧长.熟练掌握弧长的计算公式是解题的关键.
根据弧长的计算公式求解作答即可.
【详解】解:由题意知,扇形的弧长为,
故答案为:.
16.
【分析】取的中点,连接,,,,先证明是等腰直角三角形,从而得到,,进而得到是的直径,半径,由三角形内角和定理可得,从而得到,再根据弧长公式进行计算即可.
【详解】解:如图,取的中点,连接,,,,
小正方形的边长为1,
,,
由勾股定理可得:,
,
是等腰直角三角形,
,,
是的直径,半径,
,
,,
,
,
的长为,
故答案为:.
【点睛】本题考查了等腰直角三角形的判定与性质、勾股定理、圆周角定理、求弧长,熟练掌握以上知识点,添加适当的辅助线,是解题的关键.
17.
【分析】设此圆锥的母线长为R,由于圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长,则利用弧长公式得到 ,求解即可确定R的值,然后由勾股定理计算圆锥的高即可.
【详解】解:设此圆锥的母线长为R,
根据题意得,
解得R=18,即在中,,
∴由勾股定理,可得,
即此圆锥的高为.
故答案为:.
【点睛】本题考查了圆锥的相关知识、弧长的计算以及勾股定理等知识,熟练掌握圆锥的相关知识是解题关键.
18.阴影部分的面积为平方厘米
【分析】本题主要考查不规则图形面积的计算,根据图示,即可求解.
【详解】解:如图所示,
∴,
(平方厘米),
答:阴影部分的面积为平方厘米.
19.(1)平移
(2)A
(3)见解析,
【分析】(1)根据平移变换的性质即可判断.
(2)根据旋转变换的性质即可判断.
(3)利用旋转变换的性质即可画出图形,其面积为半径为2的的扇形的面积减去半径为1的的扇形的面积即可得到.
【详解】(1)解:在图①中,a先向上平移1个单位,再向右平移3个单位得到b,
则a经过一次平移变换得到b,
故答案为:平移.
(2)在图①中,b绕着A点旋转后可以得到c,则c是可以由b经过一次旋转变换得到的,其旋转中心是A点,
故答案为:A.
(3)在图②中,图形d即为所求,
EF扫过的面积.
【点睛】本题考查了作图——平移变换和旋转变换,解题的关键是掌握旋转变换和平移变换的性质.
20.(1)
(2)
【分析】(1)根据垂径定理、勾股定理列方程求解即可;
(2)求出扇形的圆心角度数,矩形的长以及等腰三角形的高,再根据各个部分面积之间的和差关系,利用扇形面积、矩形面积、三角形面积的计算方法进行计算即可.
【详解】(1)解:由题意可知,,,
设半径,则,
由垂径定理可知,,
,
为直角三角形,
在中,由勾股定理得:
,
即,
解得,
即扇形的半径;
(2)解:在中,,,
,
,
,
根据垂径定理可知:,,
,
四边形是矩形,
,
四边形是矩形,
,
,
四边形是矩形,
,即,
又,
,
,
,
,
在中,,,
,
,
,
,
根据垂径定理可知:,
且,
,
,
,
,
阴影部分的面积为.
【点睛】本题主要考查了矩形的性质与判定,扇形面积的计算,矩形面积的计算,三角形面积的计算,勾股定理,垂径定理,解一元一次方程,直角三角形的两个锐角互余,含度角的直角三角形,垂线的性质,全等三角形的判定与性质,平行线的性质等知识点,熟练掌握直角三角形的边角关系,扇形面积的计算方法以及矩形的性质与判定是解题的关键.
21.(1)盛水筒P从A点到达最高点所经过的路程为
(2)盛水筒P到水面的距离为
(3)盛水筒P从最高点开始,至少经过秒恰好在直线MN上
【分析】本题考查解直角三角形的应用,切线的性质等知识
(1)如图1中,连接.求出的度数,再利用弧长公式即可解决问题.
(2)如图2中,盛水筒浮出水面秒后,此时,过点作于,解直角三角形求出即可.
(3)如图3中,连接,解直角三角形求出,,可得的度数即可解决问题.
【详解】(1)解:由筒每分钟转圈的可得筒每秒钟转.
如图1中,连接.
图1
在中,,,,
,
,
当盛水筒P运动到延长线上时到达最高点,
∴盛水筒P从A点到达最高点所经过的路程为.
(2)解:如图,盛水筒浮出水面秒后,此时,
,
过点作于,
在中,,
∴,
∴浮出水面秒后,盛水筒距离水面;
(3)如图3中,
图3
延长交于,则为最高点,
点在上,且与相切,
当点在直线上时,此时点是切点,
连接,则,
在中,,
,
在中,,
,
,
需要的时间为(秒,
答:盛水筒从最高点开始,至少经过秒恰好在直线上.
22.
【分析】本题考查了圆锥侧面展开图的圆心角的度数,勾股定理求最值问题,掌握以上知识是解题的关键.根据条件得出圆锥的侧面展开后可得到的扇形圆心角为,进而根据勾股定理即可求解.
【详解】解:∵,,
∴.
∴圆锥的侧面展开后得到的扇形圆心角为,如图所示.
∴.
∵,
∴.
∴在中,由勾股定理得.
∴彩带长度的最小值为.
23.(1)见解析
(2)①更长;②
【分析】(1)先求证,,利用“”即可证明;
(2)①利用勾股定理计算出的长度,利用正切值求出,利用弧长公式计算弧的长度,比较大小,即可得出答案;②利用,进行计算,即可得到答案.
【详解】(1)解:证明:,
,
将线段绕点顺时针旋转得到,
,
,
,
,
,
,
,
在和中,
,
;
(2)解:① ,
,
在中,,
,
,
,
弧长度,
;
更长;
②,
,,
.
【点睛】本题主要考查了扇形的面积计算,圆周角定理,全等三角形的判定与性质,旋转的性质,掌握旋转的性质,全等三角形的判定与性质,勾股定理,弧长的计算公式,扇形面积的计算公式是解决问题的关键.
24.(1)BE=;(2)见详解;(3)
【分析】(1)由为的直径,点是的中点,可得∠ABE=,从而得是等腰直角三角形,进而即可得到结论;
(2)连接BC、BN,先证明EN∥BC,再利用圆周角定理,即可求证;
(3)连接AE,ON,先求出∠EAM=30°,再证明是等边三角形,利用扇形的面积公式,即可求解.
【详解】解:为的直径,点是的中点,
∴∠ABE=,
∵EN⊥AB,
∴∠MEB=45°,即是等腰直角三角形,
∴BE=,
故答案是:BE=;
(2)连接BC、BN,
∵为的直径,
∴∠ABC=90°,即:AB⊥BC,
∵EN⊥AB,
∴EN∥BC,
∴∠NBC=∠BNE,
∴;
(3)连接AE,ON,
∵,是等腰直角三角形,
∴EM=MB=1,BE=,
∵EN⊥AB,
∴tan∠EAM=,即∠EAM=30°,
∵,
∴∠CON=60°,NC=BE=,
∵OC=ON,
∴是等边三角形,
∴OC=NC=,
∴.
【点睛】本题主要考查圆的基本性质,锐角三角函数的定义,熟练掌握圆周角定理,扇形的面积公式,是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.9弧长及扇形的面积
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,已知点C、D在上,直径,弦、相交于点E.若,则阴影部分面积为( )
A. B. C. D.
2.已知圆锥的母线长13,圆锥的高12,则这个圆锥的侧面积是( ).
A. B. C. D.
3.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ABC=120°,则劣弧AC的长为( )
A.2π B.4π C.5π D.6π
4.如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )
A.1 B. C.2 D.
5.用一个半径为3,圆心角为120°的扇形围成一个圆锥,则这个圆锥的底面半径是( )
A.1 B.2 C.π D.2π
6.如图,以为圆心,半径为2的圆与x轴交于A,B两点,与y轴交于C,D两点,点E为上一动点,作于点F.当点E从点B出发,顺时针旋转到点D时,点F所经过的路径长为( )
A. B. C. D.
7.如图,正方形的边长为1,以点O为圆心,为半径作扇形,弧与相交于点,设正方形与扇形之间的阴影部分的面积为;然后以为对角线作正方形,又以点O为圆心,为半径作扇形,弧与相交于点,设正方形与扇形之间的阴影部分面积为;按此规律继续作下去,设正方形与扇形之间的阴影部分面积为,则等于( )
A. B. C. D.
8.若一个圆锥的底面圆的周长是6π,母线长是6,则圆锥的侧面积是( )
A.36π B.18π C.12π D.6π
9.如图,BC为直径,若,,则图中灰色区域的面积为( )
A. B. C. D.
10.如图,已知、、为上三点,连接、、、,若,,则扇形的面积为( )
A. B. C. D.
11.如图,将绕点C按顺时针旋转60°得到,已知,,则线段AB扫过的图形的面积为( )
A. B. C. D.
12.一根钢管放在V形架内,其横截面如图所示,钢管的半径是24cm,若,则劣弧AB的长是( )
A. B. C. D.
二、填空题
13.如图,AB是半径为3半圆O的直径.CD是圆中可移动的弦,且CD=3,连接 AD、BC相交于点P,弦CD从C与A重合的位置开始,绕着点O顺时针旋转120°,则交点P运动的路径长是 .
14.扇形的圆心角为,为圆心,是弧上的一点,连接,交半径于点.若,,则扇形的面积为 (结果保留).
15.一个扇形的半径为4,圆心角是,该扇形的弧长是 .
16.如图所示的网格中,每个小正方形的边长均为1,点A,B,C均在格点上,点A,B,C,D均在同一段圆弧上,若,则的长为 .
17.在数学课上,某同学用一张如图1所示的长方形纸板制做了一个扇形,并有这个扇形,围成一个圆锥模型(如图2所示),若扇形的圆心角为120°,圆锥的底面半径为6,则此圆锥的高为 .
三、解答题
18.求阴影部分面积.(单位:厘米)
19.在如图①所示的方格纸中,每个小方格都是边长为1个单位长度的正方形,a,b,c均为顶点都在格点上的三角形(每个小方格的顶点叫做格点).
(1)在图①中,a经过一次 变换(填“平移”“旋转”或“轴对称”)可以得到b;
(2)在图①中,c是可以由b经过一次旋转变换得到的,其旋转中心是点 (填“A”“B”或“C”);
(3)在图②中画出a绕点A顺时针旋转90°后得到的d,并求出线段EF所扫过的面积.
20.洛阳是十三朝古都,有“千年帝都、牡丹花城”的美誉,每到牡丹花开的季节,都会吸引无数游客前来观赏,下图是其中一处美景的俯视图,雍容华贵的牡丹花(扇形中的阴影部分)花开灿烂,上有一座供游人休息的亭子(矩形),点,分别在,上,在上,为的中点,连接交于点,延长交弧于点,已知,.
(1)求扇形的半径;
(2)若,求阴影部分的面积.
21.筒车是我国古代利用水力驱动的灌溉工具,如图,半径为的筒车按逆时针方向每分钟转圈,筒车与水面分别交于点A、B,筒车的轴心O距离水面的高度为,筒车上均匀分布着若干个盛水筒,若以某个盛水筒P刚浮出水面(点A)时开始计算时间.
(1)求盛水筒P从A点到达最高点所经过的路程;
(2)求浮出水面秒时,盛水筒P到水面的距离;
(3)若接水槽所在直线是的切线,且与直线交于点M,,直接写出盛水筒P从最高点开始,经过多长时间恰好第一次落在直线上.(参考数据:,,)
22.综合与实践
主题:制作圆锥形生日帽.
素材:一张圆形纸板、装饰彩带.
步骤1:如图1,将一个底面半径为r的圆锥侧面展开,可得到一个半径为l、圆心角为的扇形.制作圆锥形生日帽时,要先确定扇形的圆心角度数,再度量裁剪材料.
步骤2:如图2,把剪好的纸板粘合成圆锥形生日帽.
在制作好的生日帽中,,,C是的中点,现要从点A到点C再到点A之间拉一条装饰彩带,求彩带长度的最小值.
23.如图,点是内一点,,垂足为点,将线段绕点顺时针旋转得到扇形,过点作交于点,连接,与弧交于点,过点作交于点.
(1)求证:;
(2)已知,.
①通过计算比较线段和弧哪个长度更长;
②计算图中阴影部分的面积(结果保留).(参考数据:)
24.如图,在中,为的直径,为的弦,点是的中点,过点作的垂线,交于点,交于点,分别连接.
(1)与的数量关系是_______;
(2)求证:;
(3)若,求阴影部分图形的面积.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B A A B C B C B
题号 11 12
答案 D B
1.B
【分析】本题考查了等腰三角形的性质,圆周角定理和弧之间的关系,扇形的面积等.连接,根据,得出,进而得到,利用即可求解.
【详解】解:连接,
∵是直径,
∴,
∵,
∴,
∴,
∴,
故选:B.
2.B
【分析】可设圆锥底面半径长为,利用勾股定理求出,再根据圆锥侧面展开图的面积,即可求解.
【详解】可设圆锥底面半径长为,
∵,,
由勾股定理得,
圆锥侧面展开图的面积,
所以圆锥的侧面积为.
故选:B.
【点睛】本题考查圆锥的计算,解题的关键是熟练掌握圆锥的侧面积=×底面圆周长×母线长.
3.B
【分析】连接OA、OC,然后根据圆内接四边形的性质及圆周角定理求得∠AOC的度数,最后根据弧长公式求解.
【详解】解:连接OA、OC,
∵∠ABC=120°,
∴∠ADC=60°,
∴∠AOC=2∠ADC=120°,
则劣弧AC的长为:.
故选:B.
【点睛】本题考查了弧长的计算以及圆周角定理、圆内接四边形的性质,解答本题的关键是掌握弧长公式.
4.A
【分析】设AT交⊙O于C,连接BC,如图,利用切线的性质得到∠ABT=90°,则可判断△ABT为等腰直角三角形,再根据圆周角定理得到∠ACB=90°,所以BC=AC=TC,则S弓形AC=S弓形BC,然后利用阴影部分的面积=S△BTC=S△ABT进行计算.
【详解】解:设AT交⊙O于C,连接BC,如图,
∵BT是⊙O的切线,
∴BT⊥AB,
∴∠ABT=90°,
∵∠ATB=45°,
∴△ABT为等腰直角三角形,
∵AB为直径,
∴∠ACB=90°,
∴BC⊥AT,
∴BC=AC=TC,
∴S弓形AC=S弓形BC,
∴阴影部分的面积=S△BTC=S△ABT=××2×2=1.
故选:A.
【点睛】本题考查求不规则图形的面积,解决问题的关键是把不规则图形转化为规则图形,本题是利用割补法把不规则图形转化为规则图形.
5.A
【分析】设该圆锥底面圆的半径为rcm,则可根据圆锥的侧面展开图为扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2πr=,然后解方程即可.
【详解】解:设该圆锥底面圆的半径为r,
根据题意得2πr=,
解得r=1,
即该圆锥底面圆的半径为1.
故选:A.
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
6.B
【分析】连接,,,先由圆周角定理得到点F的运动轨迹是以为直径的圆上,且点O在圆上,进而得到当点E从点B出发,顺时针旋转到点D时,点F所经过的路径长为的长;根据勾股定理和锐角三角函数求得,,则所对的圆心角的度数为,利用弧长公式求得的长即可求解.
【详解】解:连接,,,
∵,
∴,
∴点F的运动轨迹是以为直径的圆上,且点O在圆上,
当点E在点B处时,,点F与O重合;
当点E在点D处时,∵以为圆心,半径为2的圆与x轴交于A,B两点,与y轴交于C,D两点,
∴即,点F与A重合,
∴当点E从点B出发,顺时针旋转到点D时,点F所经过的路径长为的长;
∵,,,
∴,
∵,
∴,,
∴,则所对的圆心角的度数为,
∴的长为,即点F所经过的路径长为,
故选:B.
【点睛】本题考查圆周角定理、解直角三角形、弧长公式、坐标与图形等知识,正确得到点F的运动轨迹以及点F所经过的路径长为的长是解答的关键.
7.C
【分析】分别求出和,找到阴影部分面积的变化规律,即可得到.
【详解】解:正方形的边长为1,
则正方形的面积为1, ,以O为圆心,为半径作扇形,得到,
以为对角线作正方形,又以O为圆心,为半径作扇形,得到,
以此类推得到﹣,
故.
故选:C.
【点睛】此题考查了正方形的性质、扇形面积公式等知识,找到图形面积的规律是解题的关键.
8.B
【分析】根据圆锥侧面面积公式求解即可.
【详解】解:S圆锥侧面积=.
故选择B.
【点睛】本题考查圆锥的侧面积,掌握扇形面积公式是解题关键.
9.C
【分析】由,则∠B+∠C=100°,从而得出∠ODB+∠OEC=100°,根据三角形的内角和定理得∠BOD+∠COE=160°,再由扇形的面积公式得出答案.
【详解】解:如图:
∵∠A=80°,
∴∠B+∠C=100°,
∵BC=6,
∴OB=OC=OD=OE=3,
∴∠ODB+∠OEC=100°,
即(180°∠BOD)+(180°∠COE)=100°,
整理可得:∠BOD+∠COE=160°,
∴图中灰色区域的面积为;
故选:C.
【点睛】本题考查了扇形面积的计算和三角形的内角和定理,是基础知识要熟练掌握.
10.B
【分析】根据圆周角定理你求出∠AOB,带入扇形的面积公式运算即可.
【详解】解:∵∠ACB=50°,
∴∠AOB=2∠ACB=100°,
∴扇形AOB的面积,故选:B.
【点睛】本题考查了圆周角定理求面积公式,熟悉掌握公式是解决本题的关键.
11.D
【分析】根据图形可以得出扫过的图形的面积,由旋转的性质就可以得出,从而得出扫过的图形的面积求出其值即可.
【详解】解:∵绕点C旋转60°得到,
∴,
∴,.
∵扫过的图形的面积,
∴扫过的图形的面积,
∴扫过的图形的面积.
故选:D.
【点睛】本题考查了旋转的性质的运用,全等三角形的性质的运用,扇形的面积公式的运用,解答时根据旋转的性质求解是关键.
12.B
【分析】先利用v形架与圆的关系求出∠C+∠AOB=180°,由∠C=60°,可求∠AOB=120°,由OB=24cm,利用弧长公式求即可.
【详解】解:∵AC与BC是圆的切线,
∴OA⊥AC,OB⊥CB,
∴∠OAC=∠OBC=90°,
∴∠C+∠AOB=360°-∠OAC-∠OBC=360°-90°-90°=180°,
∵∠C=60°,
∴∠AOB=180°-60°=120°,
∵OB=24cm,
∴=cm.
故选择B.
【点睛】本题考查直线与圆的位置关系,四边形内角和,弧长公式,掌握直线与圆的位置关系,四边形内角和,弧长公式是解题关键.
13.
【分析】根据题意找到不变的量可作下图,求得点P的轨迹也是圆,圆心角度数为120度,再根据AB的长求出⊙O’的半径即可求出点P运动的路径长
【详解】连接AC,BD,OC,OD,∵AB是半径为3半圆O的直径
∴CO=DO=CD=3,
∴△COD为等边三角形,
∠COD=60°,
则∠DAC=∠DBC=30°,
又AB为直径得∠APB=180°-∠DAB-∠CBA=120°
由定径对定角,得出P轨迹为圆,
以AB为底作顶角为120°的等腰△ABO’,
∵AB=6,求得AO’=2
故P的运动轨迹为120°的圆弧,
【点睛】此题主要考查圆内综合问题,解题的关键是熟知圆周角定理与弧长公式.
14.
【分析】过作于,交于,则,根据勾股定理和扇形的面积公式即可得到结论.
【详解】解:过作于,交于,
则,
,
,
,
,
,
,
,
,
,
,
,
扇形的面积,
故答案为:.
【点睛】本题考查了扇形面积的计算,勾股定理,垂径定理,直角三角形的性质,正确地作出辅助线是解题的关键.
15.
【分析】本题考查了弧长.熟练掌握弧长的计算公式是解题的关键.
根据弧长的计算公式求解作答即可.
【详解】解:由题意知,扇形的弧长为,
故答案为:.
16.
【分析】取的中点,连接,,,,先证明是等腰直角三角形,从而得到,,进而得到是的直径,半径,由三角形内角和定理可得,从而得到,再根据弧长公式进行计算即可.
【详解】解:如图,取的中点,连接,,,,
小正方形的边长为1,
,,
由勾股定理可得:,
,
是等腰直角三角形,
,,
是的直径,半径,
,
,,
,
,
的长为,
故答案为:.
【点睛】本题考查了等腰直角三角形的判定与性质、勾股定理、圆周角定理、求弧长,熟练掌握以上知识点,添加适当的辅助线,是解题的关键.
17.
【分析】设此圆锥的母线长为R,由于圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长,则利用弧长公式得到 ,求解即可确定R的值,然后由勾股定理计算圆锥的高即可.
【详解】解:设此圆锥的母线长为R,
根据题意得,
解得R=18,即在中,,
∴由勾股定理,可得,
即此圆锥的高为.
故答案为:.
【点睛】本题考查了圆锥的相关知识、弧长的计算以及勾股定理等知识,熟练掌握圆锥的相关知识是解题关键.
18.阴影部分的面积为平方厘米
【分析】本题主要考查不规则图形面积的计算,根据图示,即可求解.
【详解】解:如图所示,
∴,
(平方厘米),
答:阴影部分的面积为平方厘米.
19.(1)平移
(2)A
(3)见解析,
【分析】(1)根据平移变换的性质即可判断.
(2)根据旋转变换的性质即可判断.
(3)利用旋转变换的性质即可画出图形,其面积为半径为2的的扇形的面积减去半径为1的的扇形的面积即可得到.
【详解】(1)解:在图①中,a先向上平移1个单位,再向右平移3个单位得到b,
则a经过一次平移变换得到b,
故答案为:平移.
(2)在图①中,b绕着A点旋转后可以得到c,则c是可以由b经过一次旋转变换得到的,其旋转中心是A点,
故答案为:A.
(3)在图②中,图形d即为所求,
EF扫过的面积.
【点睛】本题考查了作图——平移变换和旋转变换,解题的关键是掌握旋转变换和平移变换的性质.
20.(1)
(2)
【分析】(1)根据垂径定理、勾股定理列方程求解即可;
(2)求出扇形的圆心角度数,矩形的长以及等腰三角形的高,再根据各个部分面积之间的和差关系,利用扇形面积、矩形面积、三角形面积的计算方法进行计算即可.
【详解】(1)解:由题意可知,,,
设半径,则,
由垂径定理可知,,
,
为直角三角形,
在中,由勾股定理得:
,
即,
解得,
即扇形的半径;
(2)解:在中,,,
,
,
,
根据垂径定理可知:,,
,
四边形是矩形,
,
四边形是矩形,
,
,
四边形是矩形,
,即,
又,
,
,
,
,
在中,,,
,
,
,
,
根据垂径定理可知:,
且,
,
,
,
,
阴影部分的面积为.
【点睛】本题主要考查了矩形的性质与判定,扇形面积的计算,矩形面积的计算,三角形面积的计算,勾股定理,垂径定理,解一元一次方程,直角三角形的两个锐角互余,含度角的直角三角形,垂线的性质,全等三角形的判定与性质,平行线的性质等知识点,熟练掌握直角三角形的边角关系,扇形面积的计算方法以及矩形的性质与判定是解题的关键.
21.(1)盛水筒P从A点到达最高点所经过的路程为
(2)盛水筒P到水面的距离为
(3)盛水筒P从最高点开始,至少经过秒恰好在直线MN上
【分析】本题考查解直角三角形的应用,切线的性质等知识
(1)如图1中,连接.求出的度数,再利用弧长公式即可解决问题.
(2)如图2中,盛水筒浮出水面秒后,此时,过点作于,解直角三角形求出即可.
(3)如图3中,连接,解直角三角形求出,,可得的度数即可解决问题.
【详解】(1)解:由筒每分钟转圈的可得筒每秒钟转.
如图1中,连接.
图1
在中,,,,
,
,
当盛水筒P运动到延长线上时到达最高点,
∴盛水筒P从A点到达最高点所经过的路程为.
(2)解:如图,盛水筒浮出水面秒后,此时,
,
过点作于,
在中,,
∴,
∴浮出水面秒后,盛水筒距离水面;
(3)如图3中,
图3
延长交于,则为最高点,
点在上,且与相切,
当点在直线上时,此时点是切点,
连接,则,
在中,,
,
在中,,
,
,
需要的时间为(秒,
答:盛水筒从最高点开始,至少经过秒恰好在直线上.
22.
【分析】本题考查了圆锥侧面展开图的圆心角的度数,勾股定理求最值问题,掌握以上知识是解题的关键.根据条件得出圆锥的侧面展开后可得到的扇形圆心角为,进而根据勾股定理即可求解.
【详解】解:∵,,
∴.
∴圆锥的侧面展开后得到的扇形圆心角为,如图所示.
∴.
∵,
∴.
∴在中,由勾股定理得.
∴彩带长度的最小值为.
23.(1)见解析
(2)①更长;②
【分析】(1)先求证,,利用“”即可证明;
(2)①利用勾股定理计算出的长度,利用正切值求出,利用弧长公式计算弧的长度,比较大小,即可得出答案;②利用,进行计算,即可得到答案.
【详解】(1)解:证明:,
,
将线段绕点顺时针旋转得到,
,
,
,
,
,
,
,
在和中,
,
;
(2)解:① ,
,
在中,,
,
,
,
弧长度,
;
更长;
②,
,,
.
【点睛】本题主要考查了扇形的面积计算,圆周角定理,全等三角形的判定与性质,旋转的性质,掌握旋转的性质,全等三角形的判定与性质,勾股定理,弧长的计算公式,扇形面积的计算公式是解决问题的关键.
24.(1)BE=;(2)见详解;(3)
【分析】(1)由为的直径,点是的中点,可得∠ABE=,从而得是等腰直角三角形,进而即可得到结论;
(2)连接BC、BN,先证明EN∥BC,再利用圆周角定理,即可求证;
(3)连接AE,ON,先求出∠EAM=30°,再证明是等边三角形,利用扇形的面积公式,即可求解.
【详解】解:为的直径,点是的中点,
∴∠ABE=,
∵EN⊥AB,
∴∠MEB=45°,即是等腰直角三角形,
∴BE=,
故答案是:BE=;
(2)连接BC、BN,
∵为的直径,
∴∠ABC=90°,即:AB⊥BC,
∵EN⊥AB,
∴EN∥BC,
∴∠NBC=∠BNE,
∴;
(3)连接AE,ON,
∵,是等腰直角三角形,
∴EM=MB=1,BE=,
∵EN⊥AB,
∴tan∠EAM=,即∠EAM=30°,
∵,
∴∠CON=60°,NC=BE=,
∵OC=ON,
∴是等边三角形,
∴OC=NC=,
∴.
【点睛】本题主要考查圆的基本性质,锐角三角函数的定义,熟练掌握圆周角定理,扇形的面积公式,是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
