第三章圆同步练习(含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
第三章圆
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,是的直径,,分别与相切于点,点,若,,则的长为( )
A.1 B.2 C. D.
2.如图,在中,为直径,为弦,点C为弧的中点,以点C为切点的切线与的延长线交于点E,连接交于点F, 若,,则的长度为( )
A.3 B. C.4 D.
3.如图,正六边形螺帽的边长为2,则这个螺帽的面积是( )
A. B.6 C. D.
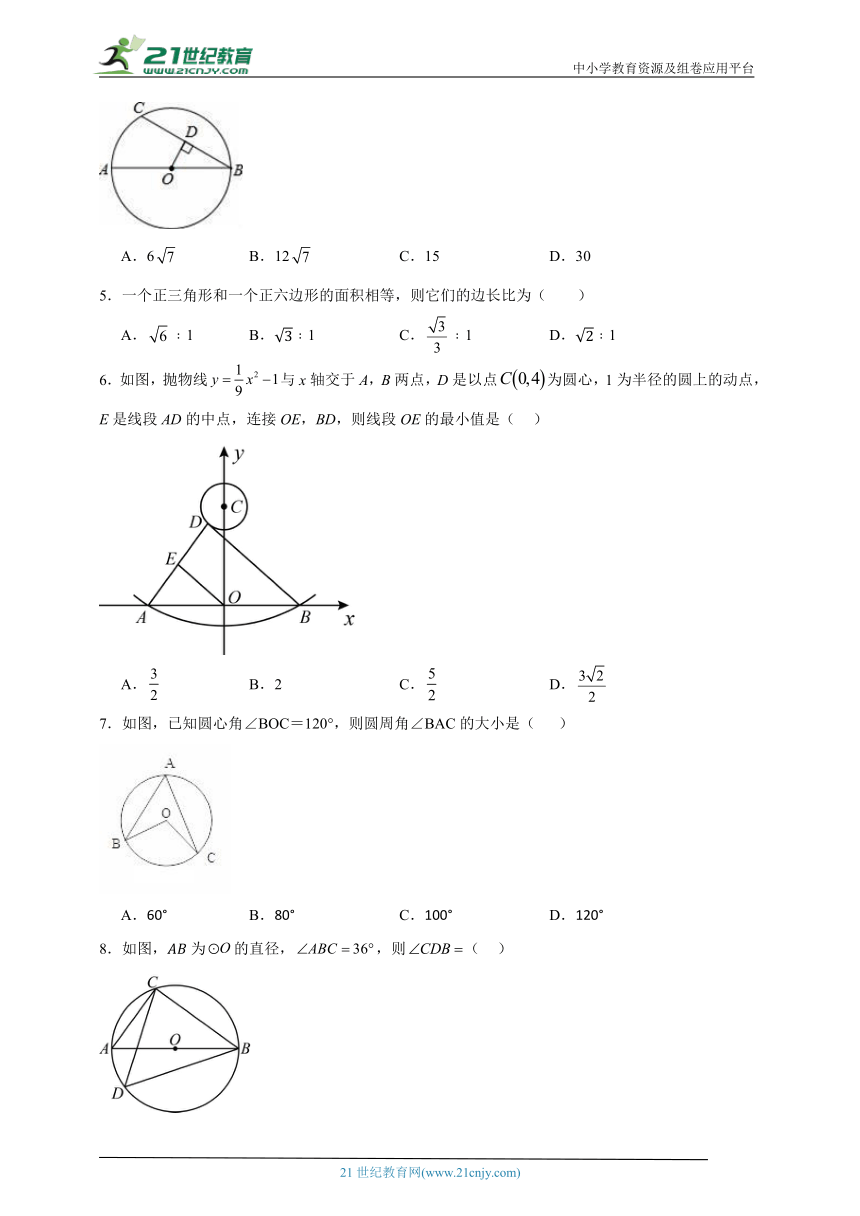
4.如图,AB为圆O的直径,BC为圆O的一弦,自O点作BC的垂线,且交BC于D点.若AB=16,BC=12,则△OBD的面积为何?( )
A.6 B.12 C.15 D.30
5.一个正三角形和一个正六边形的面积相等,则它们的边长比为( )
A.﹕1 B.﹕1 C.﹕1 D.﹕1
6.如图,抛物线与x轴交于A,B两点,D是以点为圆心,1为半径的圆上的动点,E是线段AD的中点,连接OE,BD,则线段OE的最小值是( )
A. B.2 C. D.
7.如图,已知圆心角∠BOC=120°,则圆周角∠BAC的大小是( )
A.60° B.80° C.100° D.120°
8.如图,为的直径,,则( )
A. B. C. D.
9.如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧,交AB于点E,交AC于点F,将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高为( )
A.2 B. C.4 D.
10.如图,PA 、PB是⊙O的切线,A、 B 为切点,OP交AB于点D,交⊙O于点C , 在线段AB、PA、PB、PC、CD中,已知其中两条线段的长,但还无法计算出⊙O直径的两条线段是( )
A.AB、CD B.PA、PC C.PA、AB D.PA、PB
11.如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E,若CD=,则图中阴影部分面积为( )
A. B. C. D.
12.如图,切于,切于,交于,连接,下列结论中,错误的是( ).
A. B. C. D.以上都不对
二、填空题
13.如图,AB是⊙o的直径,CD是弦,若AB=10cm,CD=8cm ,那么A、B两点到直线CD的距离之和为 .
14.如图,直径的半圆,绕点B顺时针旋转,此时点A到了点,则图中阴影部分的面积的是 (结果保留)
15.能够重合的两个圆是 .
注意:
1)半径 的两个圆是等圆;
2)同圆或等圆的半径 .
在同圆或等圆中,能够互相重合的弧叫做 .
注意:
1)等弧的长度一定 ;
2)长度相等的弧是等弧.
16.已知一个扇形的面积是,弧长是,则这个扇形的半径为 .
17.如图,四边形和均为正方形,且点,,在半圆的弧上,点,,在半圆的直径上,点,,在一条直线上,若半圆的半径为,则阴影部分的面积为 .
三、解答题
18.如图,为的切线,C为切点,D是上一点,过点D作,垂足为F,交于点E,连接并延长交于点G,连接,已知E为弧的中点.
(1)若的直径为10,求的长;
(2)试探究出与之间的数量关系,并说明你的结论(用两种方法证明)
19.如图,在的正方形网格中,每个小正方形的顶点称为格点,其中点、、、均为格点,过点,,的圆弧与线段交于点.仅用无刻度的直尺,按要求画图,保留作图痕迹.
(1)在图①中,确定所在圆的圆心.
(2)在图②中的上,确定点,使.
(3)若每个小正方形的边长均为1,则图②中的长为 .
20.如图,有一座圆弧形拱桥,桥下水面宽,为16米,拱高为4米.
(1)求桥拱的半径;
(2)若大雨过后,洪水泛滥到河面宽度为12米时,求水面涨高了多少?
21.筒车是我国古代利用水力驱动的灌溉工具,车轮缚以竹筒,旋转时低则舀水,高则泻水.如图,水力驱动筒车按逆时针方向转动,竹筒把水引至A处,水沿射线方向泻至水渠,水渠所在直线与水面平行.设筒车为,与直线交于P,Q两点,与直线交于B,C两点,恰有,连接.
(1)求证:为的切线;
(2)筒车的半径为,,.当水面上升,A,O,Q三点恰好共线时,求和的度数;
(3)在(2)的条件下,直接写出筒车在水面下的最大深度(精确到.参考值:,).
22.筒车是我国古代利用水利驱动的灌溉工具,如图所示 2,筒车按逆时针方向转动,每绕一圈需要,筒车与水面分别交于、,且. ,筒车的轴心距离水面的高度 长为,筒车上均匀分布着若干个盛水筒,若以某个盛水筒 刚浮出水面时开始计算时间.
(1)求筒车的半径;
(2)盛水桶从刚浮出水面绕到离水面最高点时,求它走过的路径长:
(3)拟修建接水槽,盛水桶绕至接水槽后自然翻落,水沿着接水槽流入农田. 所在直线与 相切,当盛水桶从浮出水面至绕到上用时时,求接水槽的长.
23.如图,为的直径,D为延长线上一点,过点D作的切线,切点为C,过点B作交的延长线于点E,连接.
(1)求证:平分;
(2)连接,交于点F,若,求的半径.
24.如图,是的外接圆,于,交于点,
(1)求证:;
(2)连结并延长交于点,延长交于,连结交于点,若平分,
①若,,求的长.
②连结,若,,求:关于的函数关系式及其定义域
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C A A B A D D D
题号 11 12
答案 C D
1.B
【分析】本题主要考查了圆周角定理、切线长定理、切线的性质、等边三角形的判定与性质、解直角三角形,由切线长定理得出,结合推出是等边三角形,得到,,由切线的性质可得,从而得到,由圆周角定理可得,最后由余弦的定义可得,即可得出答案,熟练掌握以上知识点并灵活运用是解此题的关键.
【详解】解:,分别与相切于点,点,
,
,
是等边三角形,
,,
与相切于点,
,
,
,
是直径,
,
,
,
故选:B.
2.C
【分析】本题主要考查了垂径定理的推论,切线的性质,平行线分线段成比例定理,勾股定理,连接交于H,由切线的性质和垂径定理的推论得到,则由平行线分线段成比例定理得到,据此求出,则,再利用勾股定理求出答案即可.
【详解】解:如图所示,连接交于H,
∵是切线,
∴,
∵点C为弧的中点,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
故选:C.
3.C
【分析】此题主要考查正多边形的计算问题,解题的关键是正确的构造直角三角形,然后求出长,然后求出面积即可.
【详解】解:设正六边形的中心是O,一边是,则,,过O作于,
如图,在中,,,
∴,,
∴.
这个正六边形的面积.
故选:C.
4.A
【详解】试题分析: ∵OD⊥BC,
∴BD=CD=BC=×12=6,
在Rt△BOD中,∵OB=AB=8,BD=6,
∴OD==2,
∴S△OBD=OD BD=×2×6=6.
考点:垂径定理;勾股定理.
5.A
【分析】根据题意画出图形,分别设出边长并表示出面积后即可利用面积相等得到答案.
【详解】设正三角形的边长为a,则正六边形的边长为b;
(1)过A作AD⊥BC于D,则∠BAD=30°,
AD=AB cos30°=a =a,
∴S△ABC=BC AD=×a×a=a2;
(2)连接OA、OB,过O作OD⊥AB;
∵∠AOB==60°,
∴∠AOD=30°,
OD=,
∴S△OAB=,
∴S六边形=6S△OAB=6×=,
∵S△ABC=S六边形
∴a2=
解得:a:b=:1
故选A.
【点睛】本题考查了正三角形及正六边形的性质,解答此题的关键是根据题意画出图形,结合正多边形的性质解答.
6.B
【分析】根据抛物线解析式即可得出A点与B点坐标,结合题意进一步可以得出BC长为5,利用三角形中位线性质可知OE=BD,而BD最小值即为BC长减去圆的半径,据此进一步求解即可.
【详解】∵,
∴当时,,
解得:,
∴A点与B点坐标分别为:(,0),(3,0),
即:AO=BO=3,
∴O点为AB的中点,
又∵圆心C坐标为(0,4),
∴OC=4,
∴BC长度=,
∵O点为AB的中点,E点为AD的中点,
∴OE为△ABD的中位线,
即:OE=BD,
∵D点是圆上的动点,
由图可知,BD最小值即为BC长减去圆的半径,
∴BD的最小值为4,
∴OE=BD=2,
即OE的最小值为2,
故选:B.
【点睛】本题主要考查了抛物线性质与三角形中位线性质的综合运用,熟练掌握相关概念是解题关键.
7.A
【详解】试题分析:因为圆心角∠BOC=120°,圆周角为圆心角的一半,则圆周角∠BAC是60°
考点:圆心角和圆周角的关系.
点评:在圆中,一段弧所对应的圆周角是其所对应的圆心角的一半.
8.D
【分析】题目主要考查圆周角定理和三角形内角和定理,根据题意得出,然后利用三角形内角和定理求解,再由圆周角定理即可求解.
【详解】解:∵为的直径,
∴.
∵,
∴,
∴.
故选D.
9.D
【分析】设圆锥的底面圆的半径为r,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到,解得,然后利用勾股定理计算这个圆锥的高h.
【详解】解:设圆锥的底面圆的半径为r,
根据题意得,解得,
这个圆锥的高,
故选D.
【点睛】本题主要考查了圆锥的侧面展开图和弧长公式,解题的关键在于能够熟练掌握圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
10.D
【详解】A、构造一个由半径、半弦、弦心距组成的直角三角形,根据垂径定理以及勾股定理即可计算;
B、根据切割线定理即可计算;
C、首先根据垂径定理计算AD的长,再根据勾股定理计算PD的长,连接OA,根据射影定理计算OD的长,最后根据勾股定理即可计算其半径;
D、根据切线长定理,得PA=PB.相当于只给了一条线段的长,无法计算出半径的长.
故选D.
11.C
【分析】连接,于H,如图,根据切线的性质得到,则四边形为矩形,由矩形的性质得出,则,接着计算出,,然后利用扇形的面积公式,利用图中阴影部分面积进行计算.
【详解】解:连接,过O作于H,如图,
,,
,
与相切于点D,
,
∴四边形为矩形,
,
在中,,
,
在中,
,
,,
∴图中阴影部分面积.
故选:C.
【点睛】本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了扇形面积的计算.
12.D
【分析】连接,,根据切线长定理可得,再证明,问题得解.
【详解】连接,,如图,
∵切于,切于,
∴,即是等腰三角形,
∵,,
∴,
∴,即平分,
∴,即A、B、C三项都正确,
故选:D.
【点睛】本题主要考查了切线长定理,等腰三角形的判定与性质,全等三角形的判定与性质等知识,掌握切线长定理,是解答本题的关键.
13.6cm.
【详解】试题分析:过O作OG⊥CD于G,连接OC,如图所示,
∵OG⊥CD,CD=8cm,∴G为CD的中点,即CG=DG=4cm,
在Rt△OCG中,OC=AB=5cm,CG=4cm,根据勾股定理得:OG==3cm,
又AE⊥EF,OG⊥EF,BF⊥EF,∴AE∥OG∥BF,又O为AB的中点,∴G为EF的中点,即OG为梯形AEFB的中位线,∴OG=(AE+BF),则AE+BF=2OG=6cm.故答案为6cm.
考点:1.垂径定理;2.勾股定理;3.梯形中位线定理.
14.
【分析】本题主要考查了求不规则图形的面积,旋转的性质,根据旋转的性质可得,再由 进行求解即可.
【详解】解:由旋转的性质可得,
∴
,
故答案为:.
15. 等圆 相等 相等 等弧 相等
【解析】略
16.
【分析】本题考查扇形面积公式,根据扇形面积公式直接代入求解即可得到答案.
【详解】解:∵一个扇形的面积是,弧长是,
∴,
解得:,
故答案为:.
17.
【分析】如图,设半圆圆心为O,连接OF、OD,作OH⊥AD于H,根据垂径定理可得DH=AH=AD,利用勾股定理可求出DH的长,进而根据勾股定理可求出GF的长,根据S阴影=S半圆-S正方形ABCD-S正方形ECGF,即可得答案.
【详解】如图,设半圆圆心为O,连接OF、OD,作OH⊥AD于H,
∵四边形和均为正方形,
∴∠ADC=90°,∠FGC=90°,
∵OH⊥AD,
∴DH=AH=AD,四边形CODH是矩形,
∴OC=DH
∵OD=,
∴DH2+OH2=OD2,即DH2+(2DH)2=5,
解得:DH=1,(负值舍去)
∴AD=2,OC=DH=1,
在Rt△OGF中,GF2+OG2=OF2,
∵CG=GF,
∴GF2+(OC+GF)2=5,
解得:GF=1或GF=-2(舍去),
∴S阴影=S半圆-S正方形ABCD-S正方形ECGF=-22-12=,
故答案为:
【点睛】本题考查矩形的判定于性质、正方形的性质、垂径定理及勾股定理,垂直于弦的直径平分弦,并且平分这条弦所对的两条弧;熟练掌握垂径定理是解题关键.
18.(1)
(2),证明见解析
【分析】(1)根据角之间的关系和边之间的关系得是等边三角形,在中,根据含30度角的直角三角形的性质即可得;
(2)方法一:由为等边三角形,可得,在中,根据直角三角形的性质得,即;
方法二:连接,过点O作,垂足为H,根据题意得,四边形是矩形,所以,根据等边三角形的性质得,根据边之间的关系得CE=OE,根据HL得,即可得,由此即可得.
【详解】(1)解:如图所示,连接.
∵,点E为弧的中点,
∴,,
∵为的切线,C为切点,
∴,
∴,
∵,垂足为F,
∴,
∴,
∴,
∴,
∴,
∴.
∵,
∴是等边三角形,
∴,
∴.
∵的直径为10,
∴,
∵是的直径,
∴,
在中,,,
∴,
∴;
(2)解:,证明如下
证明:方法一:如图所示,
∵,
∴,
∴.
∵,
∴为等边三角形,
∴.
∵,
∴.
∴在中,,
∴,
即;
方法二:如图所示,连接,过点O作,垂足为H,
∴,
∵,
∴四边形是矩形,
∴,
∵是等边三角形,
∴,
∵,
∴,即DE=2EH,
∵,
∴,
∴,
∴,
在和中,
,
∴,
∴,
∴.
【点睛】本题考查了切线的性质,圆周角定理,平行线的判定与性质,等边三角形的判定与性质,矩形的判定与性质,全等三角形的判定与性质,直角三角形的性质,解题的关键是掌握这些知识点.
19.(1)画图见解析
(2)画图见解析
(3)
【分析】(1)如图,连接交格线于,由为直径,弦的垂直平分线与直径的交点为,则即为圆心;
(2)取格点,连接与弧交于,由等腰三角形的性质可得:,则即为所求;
(3)如图,连接,交格线于,证明,,可得,;再利用弧长公式计算即可.
【详解】(1)解:如图,连接交格线于,则即为圆心,
(2)如图,取格点,连接与弧交于,则即为所求;
(3)如图,连接,交格线于,
∵,,
∴,
∴,,
∴,;
∴的长为.
【点睛】本题考查的是等腰三角形的性质,勾股定理的逆定理的应用,勾股定理的应用,垂径定理的应用,弧长的计算,利用网格的特点作图,掌握以上基础知识是解本题的关键.
20.(1)桥拱的半径是10米;
(2)水面涨高了2米.
【分析】本题考查勾股定理,垂径定理,关键是由勾股定理,垂径定理列出关于圆半径的方程.
(1)设桥拱的半径是米,由垂径定理求出(米,而米,由勾股定理得到,求出;
(2)由垂径定理求出的长,由勾股定理求出的长,即可求出的长.
【详解】(1)解:如图,半径,,
设桥拱的半径是米,
,
(米,
拱高为4米,
米,
,
,
,
桥拱的半径是10米;
(2)解:,
(米,
(米,
(米,
(米,
水面涨高了2米.
21.(1)见解析
(2),
(3)
【分析】(1)连接并延长交于,根据为的直径可以得到,继而得到,根据,,即可得到,即可证明为的切线;
(2)根据,解出,根据为的直径得到,进而得出,,又根据得出,故可得到;
(3)过作交于,交于,于是在等腰中,根据锐角三角函数求出长,进而求出最大深度.
【详解】(1)证明:连接并延长交于,连接,如图1,
为的直径,
,
,
又,
,
,
,
是的半径,
为的切线;
(2)解:如图2所示,
,,
,
是的直径,
,
,
,
,
,
,
,
,
;
(3)解:过作交于,交于,如图3,
为等腰直角三角形,
,
,
.
【点睛】本题主要考查圆的切线的判断,等腰三角形、圆周角定理,锐角三角函数,掌握公式定理并且灵活应用是解题的关键.
22.(1)筒车的半径为
(2)
(3)接水槽的长米
【分析】本题考查了垂径定理的应用,弧长公式,解直角三角形的应用;
(1)连接,根据垂径定理可得,在中,勾股定理建立方程,解方程即可求解;
(2)由(1)可得,进而得出点运动的圆心角为,根据弧长公式,即可求解;
(3)依题意,筒每秒钟转.延长交于点,连接,,过点作于点,过点作于点,得到是等腰直角三角形,进而利用勾股定理,即可求解.
【详解】(1)解:如图2中,连接.
∵,,
∴,
在中,,,
∴,
答:筒车的半径为;
(2)由(1)可得,
∴
∴盛水桶从刚浮出水面绕到离水面最高点时,它走过的路径长为;
(3)由筒车⊙O按逆时针方向转动,每绕一圈需要,可得筒每秒钟转.
如图所示,延长交于点,连接,,过点作于点,过点作于点,
∵当盛水桶从浮出水面至绕到上用时,
∴,
.∴,
∴
∴,
∵,
∴,
∵所在直线与 相切,即,
∴
∵,
∴
∴
∴
答:接水槽的长米.
23.(1)见解析
(2)4
【分析】本题考查相似三角形的判定和性质,切线的性质,平行线的判定和性质,直径所对的圆周角是直角、等腰三角形的性质等等:
(1)连接,根据是切线,推出,进而得出,即可求证平分;
(2)连接,通过证明,推出,设的半径为r,则,,,通过证明,得出,列出方程求解即可.
【详解】(1)证明:连接,
∵是切线,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
即平分;
(2)解:连接,
∵,,
∴,
∴,
则,
设的半径为r,则,,,
∵为的直径,
∴,
∵,,
∴,
∴,即,
解得:(负值舍去),
∴的半径为4.
24.(1)证明见解析
(2)①;②
【分析】(1)延长交于点,连接,可得,由得,再根据等角的余角相等即可证明结论;
(2)①连接,结合(1)的结论先证明,进而可得,,得出是等腰三角形,由等腰三角形三线合一性质得,继而得到垂直平分,证明,,再利用,解三角形即可;
②利用角平分线性质和面积比得出,由,得出,继而求出,再根据比例性质即可得出函数解析式.
【详解】(1)证明:如图,延长交于点,连接,
∴,
∴,
∵,
∴,
∴,
又∵,
∴,
∴;
(2)解:如图,连接,
∵,
∴,
又∵平分,
∴,
由(1)得:,
∴,
∵,
∴,,
∴,
又∵,
∴,
∴,
∴,
又∵,
∴,即点为的中点,
∴垂直平分,
∴,
∴,
又∵,
∴,
∴,
∵,
∴,即:,
又∵,
∴,
∴,
在中,,
∴,
∴,
∵是直径,
∴,
在中,,
∴,
∴,
∴;
②如图,连接,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
又∵,
∴,
∴,
∴,
∵平分,
∴点到、的距离相等,
设点到、的距离为,点到的距离为,
∴,
∴,
∴,
∵是的外接圆,,
∴在中,,
∴,
∴关于的函数关系式为.
【点睛】本题考查直角所对的圆周角是直角,同弧所对的圆周角相等,等腰三角形的判定和性质,垂直平分线的判定和性质,角平分线的性质,锐角三角函数的应用,相似三角形的判定与性质,勾股定理等知识点.利用相似三角形的性质和平行线进行等面积变换是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章圆
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,是的直径,,分别与相切于点,点,若,,则的长为( )
A.1 B.2 C. D.
2.如图,在中,为直径,为弦,点C为弧的中点,以点C为切点的切线与的延长线交于点E,连接交于点F, 若,,则的长度为( )
A.3 B. C.4 D.
3.如图,正六边形螺帽的边长为2,则这个螺帽的面积是( )
A. B.6 C. D.
4.如图,AB为圆O的直径,BC为圆O的一弦,自O点作BC的垂线,且交BC于D点.若AB=16,BC=12,则△OBD的面积为何?( )
A.6 B.12 C.15 D.30
5.一个正三角形和一个正六边形的面积相等,则它们的边长比为( )
A.﹕1 B.﹕1 C.﹕1 D.﹕1
6.如图,抛物线与x轴交于A,B两点,D是以点为圆心,1为半径的圆上的动点,E是线段AD的中点,连接OE,BD,则线段OE的最小值是( )
A. B.2 C. D.
7.如图,已知圆心角∠BOC=120°,则圆周角∠BAC的大小是( )
A.60° B.80° C.100° D.120°
8.如图,为的直径,,则( )
A. B. C. D.
9.如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧,交AB于点E,交AC于点F,将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高为( )
A.2 B. C.4 D.
10.如图,PA 、PB是⊙O的切线,A、 B 为切点,OP交AB于点D,交⊙O于点C , 在线段AB、PA、PB、PC、CD中,已知其中两条线段的长,但还无法计算出⊙O直径的两条线段是( )
A.AB、CD B.PA、PC C.PA、AB D.PA、PB
11.如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E,若CD=,则图中阴影部分面积为( )
A. B. C. D.
12.如图,切于,切于,交于,连接,下列结论中,错误的是( ).
A. B. C. D.以上都不对
二、填空题
13.如图,AB是⊙o的直径,CD是弦,若AB=10cm,CD=8cm ,那么A、B两点到直线CD的距离之和为 .
14.如图,直径的半圆,绕点B顺时针旋转,此时点A到了点,则图中阴影部分的面积的是 (结果保留)
15.能够重合的两个圆是 .
注意:
1)半径 的两个圆是等圆;
2)同圆或等圆的半径 .
在同圆或等圆中,能够互相重合的弧叫做 .
注意:
1)等弧的长度一定 ;
2)长度相等的弧是等弧.
16.已知一个扇形的面积是,弧长是,则这个扇形的半径为 .
17.如图,四边形和均为正方形,且点,,在半圆的弧上,点,,在半圆的直径上,点,,在一条直线上,若半圆的半径为,则阴影部分的面积为 .
三、解答题
18.如图,为的切线,C为切点,D是上一点,过点D作,垂足为F,交于点E,连接并延长交于点G,连接,已知E为弧的中点.
(1)若的直径为10,求的长;
(2)试探究出与之间的数量关系,并说明你的结论(用两种方法证明)
19.如图,在的正方形网格中,每个小正方形的顶点称为格点,其中点、、、均为格点,过点,,的圆弧与线段交于点.仅用无刻度的直尺,按要求画图,保留作图痕迹.
(1)在图①中,确定所在圆的圆心.
(2)在图②中的上,确定点,使.
(3)若每个小正方形的边长均为1,则图②中的长为 .
20.如图,有一座圆弧形拱桥,桥下水面宽,为16米,拱高为4米.
(1)求桥拱的半径;
(2)若大雨过后,洪水泛滥到河面宽度为12米时,求水面涨高了多少?
21.筒车是我国古代利用水力驱动的灌溉工具,车轮缚以竹筒,旋转时低则舀水,高则泻水.如图,水力驱动筒车按逆时针方向转动,竹筒把水引至A处,水沿射线方向泻至水渠,水渠所在直线与水面平行.设筒车为,与直线交于P,Q两点,与直线交于B,C两点,恰有,连接.
(1)求证:为的切线;
(2)筒车的半径为,,.当水面上升,A,O,Q三点恰好共线时,求和的度数;
(3)在(2)的条件下,直接写出筒车在水面下的最大深度(精确到.参考值:,).
22.筒车是我国古代利用水利驱动的灌溉工具,如图所示 2,筒车按逆时针方向转动,每绕一圈需要,筒车与水面分别交于、,且. ,筒车的轴心距离水面的高度 长为,筒车上均匀分布着若干个盛水筒,若以某个盛水筒 刚浮出水面时开始计算时间.
(1)求筒车的半径;
(2)盛水桶从刚浮出水面绕到离水面最高点时,求它走过的路径长:
(3)拟修建接水槽,盛水桶绕至接水槽后自然翻落,水沿着接水槽流入农田. 所在直线与 相切,当盛水桶从浮出水面至绕到上用时时,求接水槽的长.
23.如图,为的直径,D为延长线上一点,过点D作的切线,切点为C,过点B作交的延长线于点E,连接.
(1)求证:平分;
(2)连接,交于点F,若,求的半径.
24.如图,是的外接圆,于,交于点,
(1)求证:;
(2)连结并延长交于点,延长交于,连结交于点,若平分,
①若,,求的长.
②连结,若,,求:关于的函数关系式及其定义域
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C A A B A D D D
题号 11 12
答案 C D
1.B
【分析】本题主要考查了圆周角定理、切线长定理、切线的性质、等边三角形的判定与性质、解直角三角形,由切线长定理得出,结合推出是等边三角形,得到,,由切线的性质可得,从而得到,由圆周角定理可得,最后由余弦的定义可得,即可得出答案,熟练掌握以上知识点并灵活运用是解此题的关键.
【详解】解:,分别与相切于点,点,
,
,
是等边三角形,
,,
与相切于点,
,
,
,
是直径,
,
,
,
故选:B.
2.C
【分析】本题主要考查了垂径定理的推论,切线的性质,平行线分线段成比例定理,勾股定理,连接交于H,由切线的性质和垂径定理的推论得到,则由平行线分线段成比例定理得到,据此求出,则,再利用勾股定理求出答案即可.
【详解】解:如图所示,连接交于H,
∵是切线,
∴,
∵点C为弧的中点,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
故选:C.
3.C
【分析】此题主要考查正多边形的计算问题,解题的关键是正确的构造直角三角形,然后求出长,然后求出面积即可.
【详解】解:设正六边形的中心是O,一边是,则,,过O作于,
如图,在中,,,
∴,,
∴.
这个正六边形的面积.
故选:C.
4.A
【详解】试题分析: ∵OD⊥BC,
∴BD=CD=BC=×12=6,
在Rt△BOD中,∵OB=AB=8,BD=6,
∴OD==2,
∴S△OBD=OD BD=×2×6=6.
考点:垂径定理;勾股定理.
5.A
【分析】根据题意画出图形,分别设出边长并表示出面积后即可利用面积相等得到答案.
【详解】设正三角形的边长为a,则正六边形的边长为b;
(1)过A作AD⊥BC于D,则∠BAD=30°,
AD=AB cos30°=a =a,
∴S△ABC=BC AD=×a×a=a2;
(2)连接OA、OB,过O作OD⊥AB;
∵∠AOB==60°,
∴∠AOD=30°,
OD=,
∴S△OAB=,
∴S六边形=6S△OAB=6×=,
∵S△ABC=S六边形
∴a2=
解得:a:b=:1
故选A.
【点睛】本题考查了正三角形及正六边形的性质,解答此题的关键是根据题意画出图形,结合正多边形的性质解答.
6.B
【分析】根据抛物线解析式即可得出A点与B点坐标,结合题意进一步可以得出BC长为5,利用三角形中位线性质可知OE=BD,而BD最小值即为BC长减去圆的半径,据此进一步求解即可.
【详解】∵,
∴当时,,
解得:,
∴A点与B点坐标分别为:(,0),(3,0),
即:AO=BO=3,
∴O点为AB的中点,
又∵圆心C坐标为(0,4),
∴OC=4,
∴BC长度=,
∵O点为AB的中点,E点为AD的中点,
∴OE为△ABD的中位线,
即:OE=BD,
∵D点是圆上的动点,
由图可知,BD最小值即为BC长减去圆的半径,
∴BD的最小值为4,
∴OE=BD=2,
即OE的最小值为2,
故选:B.
【点睛】本题主要考查了抛物线性质与三角形中位线性质的综合运用,熟练掌握相关概念是解题关键.
7.A
【详解】试题分析:因为圆心角∠BOC=120°,圆周角为圆心角的一半,则圆周角∠BAC是60°
考点:圆心角和圆周角的关系.
点评:在圆中,一段弧所对应的圆周角是其所对应的圆心角的一半.
8.D
【分析】题目主要考查圆周角定理和三角形内角和定理,根据题意得出,然后利用三角形内角和定理求解,再由圆周角定理即可求解.
【详解】解:∵为的直径,
∴.
∵,
∴,
∴.
故选D.
9.D
【分析】设圆锥的底面圆的半径为r,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到,解得,然后利用勾股定理计算这个圆锥的高h.
【详解】解:设圆锥的底面圆的半径为r,
根据题意得,解得,
这个圆锥的高,
故选D.
【点睛】本题主要考查了圆锥的侧面展开图和弧长公式,解题的关键在于能够熟练掌握圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
10.D
【详解】A、构造一个由半径、半弦、弦心距组成的直角三角形,根据垂径定理以及勾股定理即可计算;
B、根据切割线定理即可计算;
C、首先根据垂径定理计算AD的长,再根据勾股定理计算PD的长,连接OA,根据射影定理计算OD的长,最后根据勾股定理即可计算其半径;
D、根据切线长定理,得PA=PB.相当于只给了一条线段的长,无法计算出半径的长.
故选D.
11.C
【分析】连接,于H,如图,根据切线的性质得到,则四边形为矩形,由矩形的性质得出,则,接着计算出,,然后利用扇形的面积公式,利用图中阴影部分面积进行计算.
【详解】解:连接,过O作于H,如图,
,,
,
与相切于点D,
,
∴四边形为矩形,
,
在中,,
,
在中,
,
,,
∴图中阴影部分面积.
故选:C.
【点睛】本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了扇形面积的计算.
12.D
【分析】连接,,根据切线长定理可得,再证明,问题得解.
【详解】连接,,如图,
∵切于,切于,
∴,即是等腰三角形,
∵,,
∴,
∴,即平分,
∴,即A、B、C三项都正确,
故选:D.
【点睛】本题主要考查了切线长定理,等腰三角形的判定与性质,全等三角形的判定与性质等知识,掌握切线长定理,是解答本题的关键.
13.6cm.
【详解】试题分析:过O作OG⊥CD于G,连接OC,如图所示,
∵OG⊥CD,CD=8cm,∴G为CD的中点,即CG=DG=4cm,
在Rt△OCG中,OC=AB=5cm,CG=4cm,根据勾股定理得:OG==3cm,
又AE⊥EF,OG⊥EF,BF⊥EF,∴AE∥OG∥BF,又O为AB的中点,∴G为EF的中点,即OG为梯形AEFB的中位线,∴OG=(AE+BF),则AE+BF=2OG=6cm.故答案为6cm.
考点:1.垂径定理;2.勾股定理;3.梯形中位线定理.
14.
【分析】本题主要考查了求不规则图形的面积,旋转的性质,根据旋转的性质可得,再由 进行求解即可.
【详解】解:由旋转的性质可得,
∴
,
故答案为:.
15. 等圆 相等 相等 等弧 相等
【解析】略
16.
【分析】本题考查扇形面积公式,根据扇形面积公式直接代入求解即可得到答案.
【详解】解:∵一个扇形的面积是,弧长是,
∴,
解得:,
故答案为:.
17.
【分析】如图,设半圆圆心为O,连接OF、OD,作OH⊥AD于H,根据垂径定理可得DH=AH=AD,利用勾股定理可求出DH的长,进而根据勾股定理可求出GF的长,根据S阴影=S半圆-S正方形ABCD-S正方形ECGF,即可得答案.
【详解】如图,设半圆圆心为O,连接OF、OD,作OH⊥AD于H,
∵四边形和均为正方形,
∴∠ADC=90°,∠FGC=90°,
∵OH⊥AD,
∴DH=AH=AD,四边形CODH是矩形,
∴OC=DH
∵OD=,
∴DH2+OH2=OD2,即DH2+(2DH)2=5,
解得:DH=1,(负值舍去)
∴AD=2,OC=DH=1,
在Rt△OGF中,GF2+OG2=OF2,
∵CG=GF,
∴GF2+(OC+GF)2=5,
解得:GF=1或GF=-2(舍去),
∴S阴影=S半圆-S正方形ABCD-S正方形ECGF=-22-12=,
故答案为:
【点睛】本题考查矩形的判定于性质、正方形的性质、垂径定理及勾股定理,垂直于弦的直径平分弦,并且平分这条弦所对的两条弧;熟练掌握垂径定理是解题关键.
18.(1)
(2),证明见解析
【分析】(1)根据角之间的关系和边之间的关系得是等边三角形,在中,根据含30度角的直角三角形的性质即可得;
(2)方法一:由为等边三角形,可得,在中,根据直角三角形的性质得,即;
方法二:连接,过点O作,垂足为H,根据题意得,四边形是矩形,所以,根据等边三角形的性质得,根据边之间的关系得CE=OE,根据HL得,即可得,由此即可得.
【详解】(1)解:如图所示,连接.
∵,点E为弧的中点,
∴,,
∵为的切线,C为切点,
∴,
∴,
∵,垂足为F,
∴,
∴,
∴,
∴,
∴,
∴.
∵,
∴是等边三角形,
∴,
∴.
∵的直径为10,
∴,
∵是的直径,
∴,
在中,,,
∴,
∴;
(2)解:,证明如下
证明:方法一:如图所示,
∵,
∴,
∴.
∵,
∴为等边三角形,
∴.
∵,
∴.
∴在中,,
∴,
即;
方法二:如图所示,连接,过点O作,垂足为H,
∴,
∵,
∴四边形是矩形,
∴,
∵是等边三角形,
∴,
∵,
∴,即DE=2EH,
∵,
∴,
∴,
∴,
在和中,
,
∴,
∴,
∴.
【点睛】本题考查了切线的性质,圆周角定理,平行线的判定与性质,等边三角形的判定与性质,矩形的判定与性质,全等三角形的判定与性质,直角三角形的性质,解题的关键是掌握这些知识点.
19.(1)画图见解析
(2)画图见解析
(3)
【分析】(1)如图,连接交格线于,由为直径,弦的垂直平分线与直径的交点为,则即为圆心;
(2)取格点,连接与弧交于,由等腰三角形的性质可得:,则即为所求;
(3)如图,连接,交格线于,证明,,可得,;再利用弧长公式计算即可.
【详解】(1)解:如图,连接交格线于,则即为圆心,
(2)如图,取格点,连接与弧交于,则即为所求;
(3)如图,连接,交格线于,
∵,,
∴,
∴,,
∴,;
∴的长为.
【点睛】本题考查的是等腰三角形的性质,勾股定理的逆定理的应用,勾股定理的应用,垂径定理的应用,弧长的计算,利用网格的特点作图,掌握以上基础知识是解本题的关键.
20.(1)桥拱的半径是10米;
(2)水面涨高了2米.
【分析】本题考查勾股定理,垂径定理,关键是由勾股定理,垂径定理列出关于圆半径的方程.
(1)设桥拱的半径是米,由垂径定理求出(米,而米,由勾股定理得到,求出;
(2)由垂径定理求出的长,由勾股定理求出的长,即可求出的长.
【详解】(1)解:如图,半径,,
设桥拱的半径是米,
,
(米,
拱高为4米,
米,
,
,
,
桥拱的半径是10米;
(2)解:,
(米,
(米,
(米,
(米,
水面涨高了2米.
21.(1)见解析
(2),
(3)
【分析】(1)连接并延长交于,根据为的直径可以得到,继而得到,根据,,即可得到,即可证明为的切线;
(2)根据,解出,根据为的直径得到,进而得出,,又根据得出,故可得到;
(3)过作交于,交于,于是在等腰中,根据锐角三角函数求出长,进而求出最大深度.
【详解】(1)证明:连接并延长交于,连接,如图1,
为的直径,
,
,
又,
,
,
,
是的半径,
为的切线;
(2)解:如图2所示,
,,
,
是的直径,
,
,
,
,
,
,
,
,
;
(3)解:过作交于,交于,如图3,
为等腰直角三角形,
,
,
.
【点睛】本题主要考查圆的切线的判断,等腰三角形、圆周角定理,锐角三角函数,掌握公式定理并且灵活应用是解题的关键.
22.(1)筒车的半径为
(2)
(3)接水槽的长米
【分析】本题考查了垂径定理的应用,弧长公式,解直角三角形的应用;
(1)连接,根据垂径定理可得,在中,勾股定理建立方程,解方程即可求解;
(2)由(1)可得,进而得出点运动的圆心角为,根据弧长公式,即可求解;
(3)依题意,筒每秒钟转.延长交于点,连接,,过点作于点,过点作于点,得到是等腰直角三角形,进而利用勾股定理,即可求解.
【详解】(1)解:如图2中,连接.
∵,,
∴,
在中,,,
∴,
答:筒车的半径为;
(2)由(1)可得,
∴
∴盛水桶从刚浮出水面绕到离水面最高点时,它走过的路径长为;
(3)由筒车⊙O按逆时针方向转动,每绕一圈需要,可得筒每秒钟转.
如图所示,延长交于点,连接,,过点作于点,过点作于点,
∵当盛水桶从浮出水面至绕到上用时,
∴,
.∴,
∴
∴,
∵,
∴,
∵所在直线与 相切,即,
∴
∵,
∴
∴
∴
答:接水槽的长米.
23.(1)见解析
(2)4
【分析】本题考查相似三角形的判定和性质,切线的性质,平行线的判定和性质,直径所对的圆周角是直角、等腰三角形的性质等等:
(1)连接,根据是切线,推出,进而得出,即可求证平分;
(2)连接,通过证明,推出,设的半径为r,则,,,通过证明,得出,列出方程求解即可.
【详解】(1)证明:连接,
∵是切线,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
即平分;
(2)解:连接,
∵,,
∴,
∴,
则,
设的半径为r,则,,,
∵为的直径,
∴,
∵,,
∴,
∴,即,
解得:(负值舍去),
∴的半径为4.
24.(1)证明见解析
(2)①;②
【分析】(1)延长交于点,连接,可得,由得,再根据等角的余角相等即可证明结论;
(2)①连接,结合(1)的结论先证明,进而可得,,得出是等腰三角形,由等腰三角形三线合一性质得,继而得到垂直平分,证明,,再利用,解三角形即可;
②利用角平分线性质和面积比得出,由,得出,继而求出,再根据比例性质即可得出函数解析式.
【详解】(1)证明:如图,延长交于点,连接,
∴,
∴,
∵,
∴,
∴,
又∵,
∴,
∴;
(2)解:如图,连接,
∵,
∴,
又∵平分,
∴,
由(1)得:,
∴,
∵,
∴,,
∴,
又∵,
∴,
∴,
∴,
又∵,
∴,即点为的中点,
∴垂直平分,
∴,
∴,
又∵,
∴,
∴,
∵,
∴,即:,
又∵,
∴,
∴,
在中,,
∴,
∴,
∵是直径,
∴,
在中,,
∴,
∴,
∴;
②如图,连接,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
又∵,
∴,
∴,
∴,
∵平分,
∴点到、的距离相等,
设点到、的距离为,点到的距离为,
∴,
∴,
∴,
∵是的外接圆,,
∴在中,,
∴,
∴关于的函数关系式为.
【点睛】本题考查直角所对的圆周角是直角,同弧所对的圆周角相等,等腰三角形的判定和性质,垂直平分线的判定和性质,角平分线的性质,锐角三角函数的应用,相似三角形的判定与性质,勾股定理等知识点.利用相似三角形的性质和平行线进行等面积变换是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
