3.1圆同步练习(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
3.1圆
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,菱形的边,,P是上一点,,Q是边上一动点,将梯形沿直线折叠,A的对应点,当的长度最小时,的长为( )
A.5 B. C. D.7
2.已知的半径为,点在外,则的长为( )
A. B. C. D.
3.设P为外一点,若点P到的最短距离为3,最长距离为7,则的半径为( )
A.2 B.4 C.4或10 D.2或5
4.以坐标原点为圆心,以5为半径作圆,则下列各点中,一定在上的是( )
A. B. C. D.
5.已知的半径是4,点P在内,则的长可能是( )
A.3 B.4 C. D.5
6.如图,在平面直角坐标系中,O为原点,,点C为平面内一动点,,连接,点M是线段上的一点,且满足.当线段取最大值时,点M的坐标是( )
A. B. C. D.
7.已知的直径为4cm.若点P到圆心O的距离为3cm,则点P( )
A.在上 B.在内 C.在外 D.无法确定
8.平面内一点离上的点最近距离为,离上的点最远距离为,则的半径为( )
A. B.或 C. D.或
9.已知⊙O的半径为5,点P到圆心O的距离为4,那么点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.点P与圆心O重合
10.如图,在中,,,,点E是中点.以B为圆心,为半径画圆,则点E与的位置关系是( )
A.点E在内 B.点E在上 C.点E在外 D.无法判断
11.若的半径为8cm,点P到圆心的距离为7cm,则点P与的位置关系( )
A.P在内 B.P在上 C.P在外 D.无法确定
12.已知的半径为4,若,则点P与的位置关系是( )
A.点P在上 B.点P在内 C.点P在外 D.无法判断
二、填空题
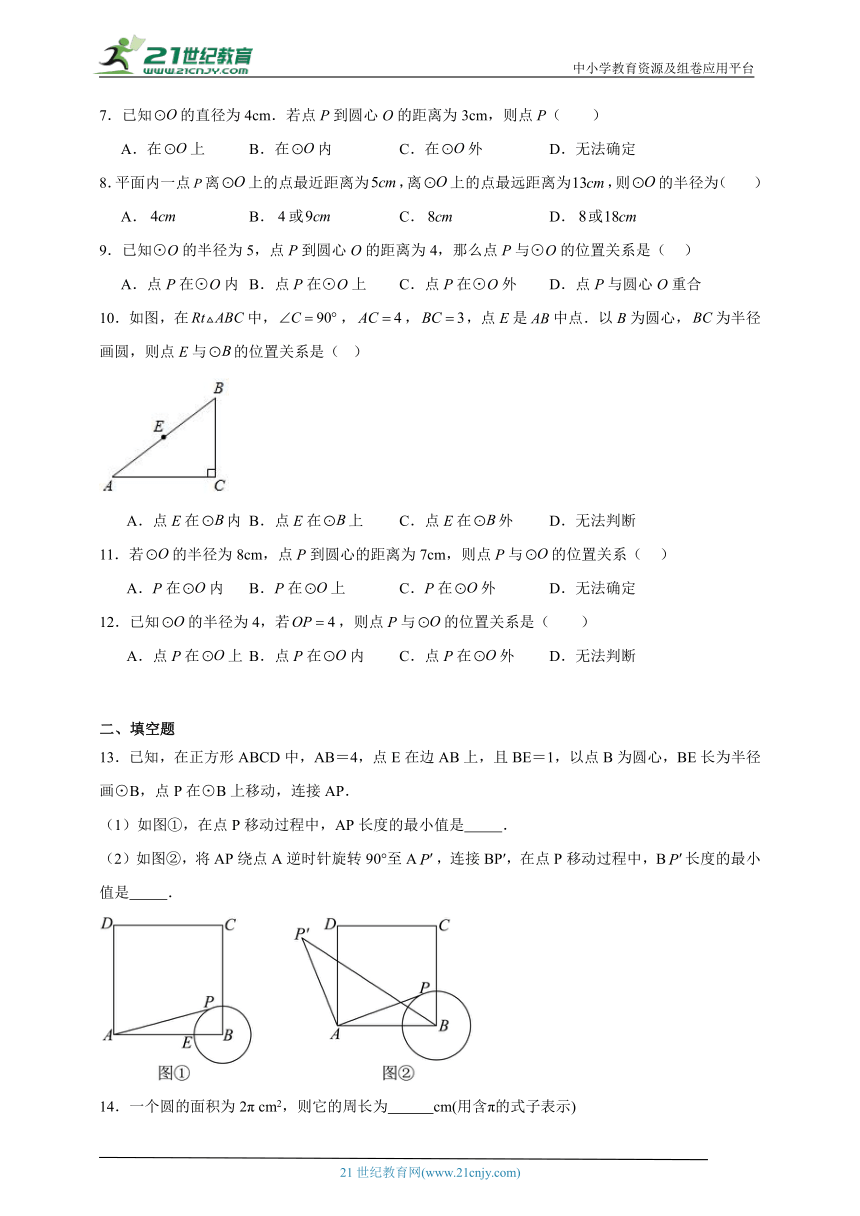
13.已知,在正方形ABCD中,AB=4,点E在边AB上,且BE=1,以点B为圆心,BE长为半径画⊙B,点P在⊙B上移动,连接AP.
(1)如图①,在点P移动过程中,AP长度的最小值是 .
(2)如图②,将AP绕点A逆时针旋转90°至A,连接BP′,在点P移动过程中,B长度的最小值是 .
14.一个圆的面积为2π cm2,则它的周长为 cm(用含π的式子表示)
15.已知平面上点P到圆周上的点的最长距离为8,最短距离为4,则此圆的半径为 .
16.如图,在矩形中,,,点E,F分别为边上的点,且,G为中点,P为边上一动点,则的最小值为 .
17.已知⊙A的半径为5,圆心A(4,3),坐标原点O与⊙A的位置关系是 .
三、解答题
18.数学兴趣小组探究平面内横、纵坐标满足特定关系的动点的运动轨迹问题:
(1)组长提出问题:动点随着t的变化形成的运动轨迹是什么
甲同学的思考:t取3个特殊值得到3个点坐标,发现3点在一条直线上,可以利用待定系数法求出该直线的表达式;乙同学的思考:令,,通过消去t得到y与x的函数关系式.
______(填甲或乙)同学的方法更严谨,点运动轨迹的函数表达式为______;
(2)如图,在平面直角坐标系中,已知点,,Q为坐标系内一点且,点M从点A出发以每秒8个单位的速度沿x轴向左运动,同时点N从点O出发以每秒6个单位的速度沿y轴向上运动,点P是MN的中点,设运动时间为t.求点P的运动轨迹的函数表达式,并计算当时PQ的最小值;
(3)老师给出坐标平面内两个动点:,.
丙学说:点T、K的运动轨迹都是直线;丁同学说:点T、K在运动过程中不可能重合;请你判断两人结论是否正确并说明理由.
19.我们规定:如果一个三角形有一边上的中线等于这条边的一半,那么称这个三角形为“智慧三角形”.
理解:
(1)如图1,已知A、B是⊙O上两点,请在圆上找出满足条件的点C,使△ABC为“智慧三角形”(画出点C的位置,保留作图痕迹);
(2)如图3,在平面直角坐标系xOy中,⊙O的半径为1,点Q是直线y=3上的一点,若在⊙O上存在一点P,使得△OPQ为“智慧三角形”,当其面积取得最小值时,直接写出此时PQ的长和点Q的坐标
20.【问题探究】
(1)如图1,在四边形中,,是的中点,F是上一动点(足够长),将沿折叠,得到,点B的对应点为P,连接,求的最小值;
【问题解决】
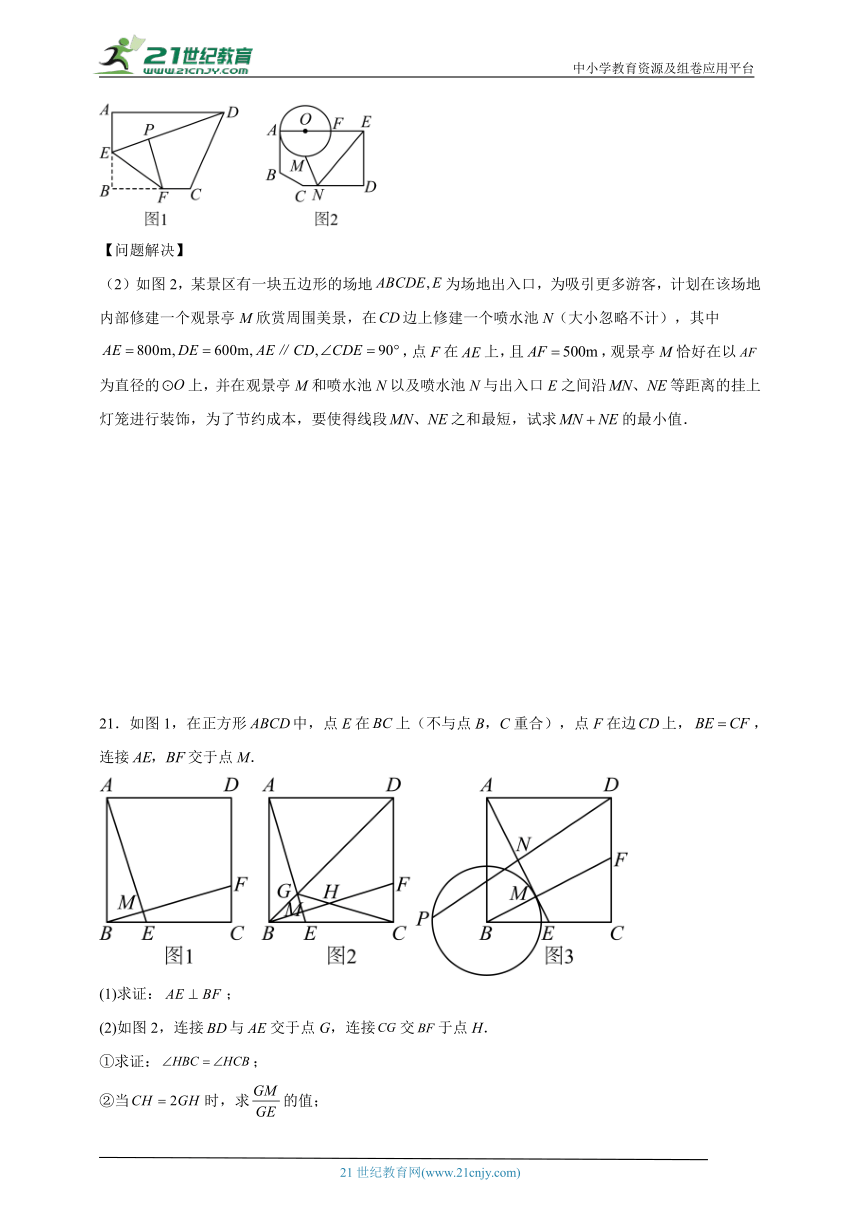
(2)如图2,某景区有一块五边形的场地为场地出入口,为吸引更多游客,计划在该场地内部修建一个观景亭M欣赏周围美景,在边上修建一个喷水池N(大小忽略不计),其中,点F在上,且,观景亭M恰好在以为直径的上,并在观景亭M和喷水池N以及喷水池N与出入口E之间沿等距离的挂上灯笼进行装饰,为了节约成本,要使得线段之和最短,试求的最小值.
21.如图1,在正方形中,点E在上(不与点B,C重合),点F在边上,,连接交于点M.
(1)求证:;
(2)如图2,连接与交于点G,连接交于点H.
①求证:;
②当时,求的值;
(3)如图3,若E是的中点,以点B为圆心,为半径作,P是上的一个动点,连接交于点N,则的最大值为 .
22.如图1,在中,点D是边上的中点.、分别垂直射线于点E、F.
(1)求证:;
(2)求证:;
(3)如图2,在矩形中,为直径的半圆O上有一个动点P,连接、.利用图1中得到的结论:探求的最小值是多少.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D D A B A A C B A A
题号 11 12
答案 A A
1.D
【分析】作于,根据菱形的性质可判断为等边三角形,则,,再利用勾股定理计算出,再利用点与圆的位置关系得到当点在上时,的值最小,即可求出.
【详解】作于,如图,
菱形的边,,
为等边三角形,
,,
,
,
在中,
.
梯形沿直线折叠,A的对应点,
点 在以点为圆心,为半径的弧上,
当点在上时,的值最小,此时,
∵,
,
,
故选:D.
【点睛】本题考查了菱形的性质,折叠的性质,圆的基本性质,解决本题的关键是确定点在上时,的值最小.
2.D
【分析】本题考查了点和圆的位置关系,熟悉点和圆的位置关系的判断是关键.根据点到圆心的距离和圆的半径之间的数量关系,即可判断点和圆的位置关系.点到圆心的距离小于圆的半径,则点在圆内;点到圆心的距离等于圆心的半径,则点在圆上;点到圆心的距离大于圆的半径,则点在圆外.
【详解】解:的半径为,点在外,
,
故选:D.
3.A
【分析】根据P为⊙O外一点,若点P到⊙O的最短距离为3,最长距离为7,可以得到圆的直径,从而可以求得圆的半径.
【详解】解:∵P为⊙O外一点,若点P到⊙O的最短距离为3,最长距离为7,
∴⊙O的直径为:7-3=4,
∴⊙O的半径为2,
故选:A.
【点睛】本题考查点和圆的位置关系,解题的关键是明确题意,找出所求问题需要的条件.
4.B
【分析】先根据勾股定理算出点到圆心的距离,再利用点与圆的位置关系进行判断:到圆心的距离等于半径的点必在圆上、到圆心的距离小于半径的点必在圆内、到圆心的距离大于半径的点必在圆外.
【详解】解:A.到圆心的距离,点在内,故选项错误;
B.到圆心的距离,点在上,故选项正确;
C.到圆心的距离,点在外,故选项错误;
D.到圆心的距离,点在外,故选项错误.
故选:B
【点睛】本题考查了点与圆的位置关系以及数量关系、勾股定理,用数量关系来判断位置关系,典型的数形结合.
5.A
【分析】根据点和圆的位置与圆的半径的关系求得的范围即可解答.
【详解】解:∵的半径为4,点在内,
∴,
选项中只有3符合题意,
故选:A.
【点睛】本题考查了点和圆的位置关系,熟知点和圆的位置与圆的半径的关系是解答的关键.
6.A
【分析】由题意可得点在以点为圆心,为半径的上,在轴的负半轴上取点,连接,分别过、作,,垂足为、,先证,得,从而当取得最大值时,取得最大值,结合图形可知当,,三点共线,且点在线段上时,取得最大值,然后分别证,,利用相似三角形的性质即可求解.
【详解】解:∵点为平面内一动点,,
∴点在以点为圆心,为半径的上,
在轴的负半轴上取点,连接,分别过、作,,垂足为、,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴当取得最大值时,取得最大值,结合图形可知当,,三点共线,且点在线段上时,取得最大值,
∵,,
∴,
∴,
∵,
∴,
∵轴轴,,
∴,
∵,
∴,
∴即,
解得,
同理可得,,
∴即,
解得,
∴,
∴当线段取最大值时,点的坐标是,
故选A.
【点睛】本题主要考查了勾股定理、相似三角形的判定及性质、圆的一般概念以及坐标与图形,熟练掌握相似三角形的判定及性质是解题的关键.
7.C
【分析】利用点到圆心的距离与圆的半径之间的大小关系,进行判断即可.
【详解】解:∵的直径为4cm,
∴的半径为2cm,
∵点P到圆心O的距离为3cm,大于的半径,
∴点P在外;
故选C.
【点睛】本题考查点与圆的位置关系.熟练掌握利用点到圆心的距离与圆的半径之间的大小关系,来判断点与圆之间的位置关系,是解题的关键.
8.B
【分析】本题应分为两种情况来讨论,关键是得出:当点P在⊙O内时,直径=最近点的距离+最远点的距离;当点P在⊙O外时,直径=最远点的距离-最近点的距离.
【详解】解:点应分为位于圆的内部与外部两种情况讨论:
①如图,当点在圆内时,最近点的距离为,最远点的距离为,
则直径是,
∴半径是;
②如图,当点在圆外时,最近点的距离为,最远点的距离为,
则直径是,
∴半径是.
故选.
【点睛】本题考查了点与圆的位置关系,在解答此题时注意到分两种情况进行讨论是解决本题的关键.
9.A
【分析】根据⊙O的半径为r和点P到圆心的距离OP=d的大小关系判断即可.
【详解】解:∵⊙O的半径为5,点P到圆心O的距离为4,
而4<5,
∴点P在⊙O内,
故选:A.
【点睛】本题考查的是点与圆的位置关系,设⊙O的半径为r,点P到圆心的距离OP=d,则有:①点P在圆外 d>r;②点P在圆上 d=r;①点P在圆内 d<r.
10.A
【分析】首先利用勾股定理求得直角三角形斜边的长,然后求得点E与点B的距离,从而求得第E与圆B的位置关系.
【详解】解:在Rt△ABC中,∠C=90°,AC=4,BC=3,
由勾股定理得到:,
∵E为AB的中点,
∴BE=AB=2.5.
∵BC=3,
∴BE<BC,
∴点E在⊙B的内部,
故选:A.
【点睛】本题主要考查了勾股定理,点与圆的位置关系,直角三角形斜边上的中线,根据点到圆心的距离和圆的半径之间的数量关系,来判断点和圆的位置关系.
11.A
【分析】本题考查点与圆的位置的关系.比较点到圆心的距离与半径的大小关系,即可得出结果.
【详解】解:∵的半径为8cm,点P到圆心的距离为7cm,,
∴P在内;
故选A.
12.A
【分析】本题考查点与圆的位置关系.若圆半径为r,点到圆心的距离为d,则有:当时,点在圆外;当时,点在圆上,当时,点在圆内.判断圆的半径与大小即可解答.
【详解】解:∵的半径,点P到圆心O的距离,
∴,
∴点P在上.
故选:A
13. 3
【分析】(1)当点P在线段AB上时,AP的长度有最小值,即可求解;
(2)由“SAS”可证△PAB△AD,可得D=PB=1,点的运动路线为以D为圆心,以1为半径的圆上,则当在对角线BD上时,B最小,再利用勾股定理求对角线BD的长,则得出B的长.
【详解】解:(1)∵点P在⊙B上移动,
∴当点P在线段AB上时,AP的长度有最小值,
最小值=AB﹣PB=4﹣1=3,
故答案为:3.
(2)如图,连接BP,
由旋转得:AP=A,∠PA=90°,
∴∠PAB+∠BA=90°,
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴∠BA+∠DA=90°,
∴∠PAB=∠DA,
在△AD和△PAB中,
∴△AD△PAB(SAS),
∴D=PB=1,
∴点P在以点D为圆心,D为半径的圆上,
∴当在对角线BD上时,B最小,
在Rt△ABD中,∵AB=AD=4,
∴BD===,
∴B=BD﹣D=﹣1,
即B长度的最小值为﹣1.
故答案为:﹣1.
【点睛】本题主要考查了正方形的性质,圆的性质,全等三角形的判定及性质,解题的关键是找出线段的最小值1.
14.2π
【分析】首先根据圆的面积公式,求出圆的半径是多少;然后根据圆的周长公式,求出这个圆的周长为多少即可.
【详解】解:设圆的半径是rcm,
则πr2=2π,
解得r=,
所以它的周长为: .
故答案为2π
【点睛】此题主要考查了算术平方根的性质和应用,要熟练掌握,解答此题的关键是要明确:如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做a的算术平方根.
15.2或6
【分析】根据已知条件能求出圆的直径,即可求出半径,此题点的位置不确定所以要分类讨论.
【详解】①当点在圆外时,
∵圆外一点和圆周的最短距离为4,最长距离为8,
∴圆的直径为8﹣4=4,
∴该圆的半径是2;
②当点在圆内时,
∵点到圆周的最短距离为4,最长距离为8,
∴圆的直径=8+4=12,
∴圆的半径为6,
故答案为2或6.
【点睛】本题考查了点和圆的位置关系的应用,能根据已知条件求出圆的直径是解此题的关键.
16./
【分析】因为,点为的中点,根据直角三角形斜边上中线的性质得出,所以是以为圆心,以为半径的圆弧上的点,作关于的对称点,连接,交于,交以为圆心,以为半径的圆于,此时的值最小,最小值为的长;根据勾股定理求得,即可求得,从而得出的最小值;
【详解】解:,点为的中点,
,
是以为圆心,以为半径的圆弧上的点,
作关于的对称点,连接,交于,交以为圆心,以为半径的圆于,此时的值最小,最小值为的长;
,
,,
,
,
;
的最小值为;
故答案为:.
【点睛】本题考查了轴对称最短路线问题,矩形的性质,勾股定理,点到圆上一点的距离,判断出点的位置是解题的关键.
17.在⊙A上
【分析】先根据两点间的距离公式计算出OA,然后根据点与圆的位置关系的判定方法判断点O与⊙A的位置关系.
【详解】解:∵点A的坐标为(4,3),
∴OA==5,
∵半径为5,
∴OA=r,
∴点O在⊙A上.
故答案为:在⊙A上.
【点睛】本题考查了点与圆的位置关系:点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,当点P在圆外 d>r;当点P在圆上 d=r;当点P在圆内 d<r.
18.(1)乙,
(2)
(3)丙同学的结论错误;丁同学的说法正确.
【分析】(1)乙的方法:用表示,进而得到关于的解析式即可;
(2)分和两种情况,先求出的坐标,利用中点坐标公式,求出点坐标,根据点到圆上的距离求得的最小值,利用两点间的距离公式,求出的最小值,即可得解;
(3)①利用(1)中小远的方法,求出点的轨迹,进行判断即可.
【详解】(1)解:乙的方法更严谨,
令,,
∴,
∴,
∴点运动轨迹的函数表达式为;
故答案为:乙,;
(2)解:∵,,
∴,,
∴移动到点的位置需要的时间为:秒,
①当时,,
,,
则:;
②当时,,
∴,,即:
则:;
综上:,
令,,消去,得的运动轨迹的函数表达式为,
当时,,
∴,
∵
∴点在以为圆心,为半径的圆上,
∴的值最小值为,
(3)①∵,
令,则:;
∴,
∴点的轨迹为抛物线;
∵,令,则:,
∴;
∴点的轨迹为直线;则丙同学的结论错误
联立,整理,得:,
∵,
∴方程没有实数根,即抛物线和直线没有交点,
即点在运动过程中不可能重合,丁同学的说法正确.
【点睛】本题考查坐标与图形,二次函数和一次函数的综合应用.熟练掌握两点间的距离公式,中点坐标公式,正确的求出函数的解析式,利用二次函数的性质进行求解,是解题的关键.
19.(1)见解析;(2),Q(0,3)
【分析】(1)连结BO并且延长交圆于C1,连结AO并且延长交圆于C2,即可求解;
(2)根据“智慧三角形”的定义可得△OPQ为直角三角形,根据题意可得一条直角边为1,当斜边最短时,另一条直角边最短,则面积取得最小值,由垂线段最短可得斜边最短为3,从而得到点Q坐标,再根据勾股定理可求另一条直角边即PQ长.
【详解】解:(1)如图所示,过直径做△ABC即可;
(2)如图所示:
由“智慧三角形”的定义可得△OPQ为直角三角形,
根据题意可得一条直角边OP=1,
∴PQ最小时,△POQ的面积最小,
根据勾股定理可知,当斜边OQ最短时,PQ最小,面积取得最小值,
由垂线段最短可得斜边最短为3,即OQ=3,
∴Q(0,3),
由勾股定理可得PQ==,
∴当面积取得最小值时,点Q的坐标为(0,3),PQ的长为.
【点睛】本题考查了圆与勾股定理的综合应用,掌握圆的相关知识,熟练应用勾股定理,明确“智慧三角形”的定义是解题的关键.
20.(1);(2)
【分析】(1)由点E是的中点及折叠的性质可知,进而可得以E为圆心、以为半径的经过点A、P.用勾股定理解求出,当E、P、D三点共线时,可取最小值,,由此可解;
(2)作点E关于的对称点,连接交于点,交于点,连接,,在四边形中,,当O、M、N、四点共线时,此时最小,最小值为的长度.
【详解】解:(1)由点E是的中点及折叠的性质可知:,且点F是的角平分线与的交点.
∴以E为圆心、以为半径的经过点A、P.
∵点E是中点,,
.
在中,由勾股定理得,即,
.
由图可知:当E、P、D三点共线时,可取最小值,
,
长的最小值为.
(2)作点E关于的对称点,连接交于点,交于点,连接,,在四边形中,,当O、M、N、四点共线时,此时最小,最小值为的长度.
,由对称可知,,
.
由题意可得,
.
在中,由勾股定理得:,即,
,
,
的最小值为.
【点睛】本题考查折叠的性质,圆的基本性质,线段的最值问题,勾股定理,正确作出辅助线是解题的关键.
21.(1)见解析
(2)①见解析;②
(3)2
【分析】(1)证明,则,利用互余关系即可证明;
(2)①证明,则,再由(1)的证明即可证明;
②分别过G、H作的垂线,垂足分别为K、Q;设,则可得,则可得,由相似三角形的性质得,进而得,则由勾股定理可分别求得,从而求得结果;
(3)延长交于点W,过P作于Y,过P作交射线于点J;易证,则,从而,当最大时,最大;证明,则可得,当最大时,最大,此时点P与点W重合,Y与M重合;由面积关系求出,则可得的值,最后求得结果;
【详解】(1)证明:四边形是正方形,
,
,
,
,
,
,
即,
;
(2)①证明:四边形是正方形,
,
,
,
,
再由(1)的证明知:,
,
即;
②解:如图,分别过G、H作的垂线,垂足分别为K、Q;
则;
∵四边形为正方形,
,
,
,
设,
由①知,,
,
,
;
,
,
,
,
即,
;
,
,
,
即,
由勾股定理得:,;
,
,
,
又由(1)知,,
由勾股定理得,
;
(3)解:如图,延长交于点W,过P作于Y,过P作交射线于点J;
,
,
,
,
则当最大时,最大;
,,
,
;
,
,
;
∵点E是的中点,,
,
由勾股定理得,
,
即,
上式表明:当最大时,最大,从而最大;
此时点P与点W重合,Y与M重合;
,
,
则,
,
的最大值为;
故答案为:2.
【点睛】本题是正方形的综合,考查了正方形的性质,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,等腰三角形的判定与性质,圆上点到切线的距离最大为直径等知识,综合性较强,构造适当的辅助线,灵活运用相关知识是解题的关键.
22.(1)见详解;(2)见详解;(3)的最小值为388
【分析】(1)由题意易得,,然后可证,则问题可证;
(2)由图1及勾股定理可得:,,,进而可得,,然后根据线段的和差关系可得,,两式相加即可得证;
(3)取AB的中点F,连接PF,由(2)中结论可得:,由题意易得,要使为最小,只需满足PF的值为最小,根据圆外的点到圆上的点的最值问题可得当点O、P、F三点共线时,PF可取最小值,连接OF,交⊙O于点P,过点O作OH⊥AB于点H,进而可得,然后问题可求解.
【详解】(1)证明:∵,
∴,
∵点D是边上的中点,
∴,
∵,
∴(AAS),
∴;
(2)由图1及勾股定理可得:
,,,
由(1)可得:,,
∴,,
∵,
∴,,
∴
=,
=
=
=,
∴;
(3)取AB的中点F,连接PF,如图所示:
由(2)中结论可得:,
∵,DE是⊙O的直径,
∴,
∴,
要使为最小,只需满足PF的值为最小,根据圆外的点到圆上的点的最值问题可得当点O、P、F三点共线时,PF可取最小值,连接OF,交⊙O于点P,过点O作OH⊥AB于点H,如图所示:
∴,,
∴,
∴,
∴PF的最小值为,
∴的最小值为.
【点睛】本题主要考查圆的最值问题及勾股定理,熟练掌握圆的最值问题及勾股定理是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.1圆
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,菱形的边,,P是上一点,,Q是边上一动点,将梯形沿直线折叠,A的对应点,当的长度最小时,的长为( )
A.5 B. C. D.7
2.已知的半径为,点在外,则的长为( )
A. B. C. D.
3.设P为外一点,若点P到的最短距离为3,最长距离为7,则的半径为( )
A.2 B.4 C.4或10 D.2或5
4.以坐标原点为圆心,以5为半径作圆,则下列各点中,一定在上的是( )
A. B. C. D.
5.已知的半径是4,点P在内,则的长可能是( )
A.3 B.4 C. D.5
6.如图,在平面直角坐标系中,O为原点,,点C为平面内一动点,,连接,点M是线段上的一点,且满足.当线段取最大值时,点M的坐标是( )
A. B. C. D.
7.已知的直径为4cm.若点P到圆心O的距离为3cm,则点P( )
A.在上 B.在内 C.在外 D.无法确定
8.平面内一点离上的点最近距离为,离上的点最远距离为,则的半径为( )
A. B.或 C. D.或
9.已知⊙O的半径为5,点P到圆心O的距离为4,那么点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.点P与圆心O重合
10.如图,在中,,,,点E是中点.以B为圆心,为半径画圆,则点E与的位置关系是( )
A.点E在内 B.点E在上 C.点E在外 D.无法判断
11.若的半径为8cm,点P到圆心的距离为7cm,则点P与的位置关系( )
A.P在内 B.P在上 C.P在外 D.无法确定
12.已知的半径为4,若,则点P与的位置关系是( )
A.点P在上 B.点P在内 C.点P在外 D.无法判断
二、填空题
13.已知,在正方形ABCD中,AB=4,点E在边AB上,且BE=1,以点B为圆心,BE长为半径画⊙B,点P在⊙B上移动,连接AP.
(1)如图①,在点P移动过程中,AP长度的最小值是 .
(2)如图②,将AP绕点A逆时针旋转90°至A,连接BP′,在点P移动过程中,B长度的最小值是 .
14.一个圆的面积为2π cm2,则它的周长为 cm(用含π的式子表示)
15.已知平面上点P到圆周上的点的最长距离为8,最短距离为4,则此圆的半径为 .
16.如图,在矩形中,,,点E,F分别为边上的点,且,G为中点,P为边上一动点,则的最小值为 .
17.已知⊙A的半径为5,圆心A(4,3),坐标原点O与⊙A的位置关系是 .
三、解答题
18.数学兴趣小组探究平面内横、纵坐标满足特定关系的动点的运动轨迹问题:
(1)组长提出问题:动点随着t的变化形成的运动轨迹是什么
甲同学的思考:t取3个特殊值得到3个点坐标,发现3点在一条直线上,可以利用待定系数法求出该直线的表达式;乙同学的思考:令,,通过消去t得到y与x的函数关系式.
______(填甲或乙)同学的方法更严谨,点运动轨迹的函数表达式为______;
(2)如图,在平面直角坐标系中,已知点,,Q为坐标系内一点且,点M从点A出发以每秒8个单位的速度沿x轴向左运动,同时点N从点O出发以每秒6个单位的速度沿y轴向上运动,点P是MN的中点,设运动时间为t.求点P的运动轨迹的函数表达式,并计算当时PQ的最小值;
(3)老师给出坐标平面内两个动点:,.
丙学说:点T、K的运动轨迹都是直线;丁同学说:点T、K在运动过程中不可能重合;请你判断两人结论是否正确并说明理由.
19.我们规定:如果一个三角形有一边上的中线等于这条边的一半,那么称这个三角形为“智慧三角形”.
理解:
(1)如图1,已知A、B是⊙O上两点,请在圆上找出满足条件的点C,使△ABC为“智慧三角形”(画出点C的位置,保留作图痕迹);
(2)如图3,在平面直角坐标系xOy中,⊙O的半径为1,点Q是直线y=3上的一点,若在⊙O上存在一点P,使得△OPQ为“智慧三角形”,当其面积取得最小值时,直接写出此时PQ的长和点Q的坐标
20.【问题探究】
(1)如图1,在四边形中,,是的中点,F是上一动点(足够长),将沿折叠,得到,点B的对应点为P,连接,求的最小值;
【问题解决】
(2)如图2,某景区有一块五边形的场地为场地出入口,为吸引更多游客,计划在该场地内部修建一个观景亭M欣赏周围美景,在边上修建一个喷水池N(大小忽略不计),其中,点F在上,且,观景亭M恰好在以为直径的上,并在观景亭M和喷水池N以及喷水池N与出入口E之间沿等距离的挂上灯笼进行装饰,为了节约成本,要使得线段之和最短,试求的最小值.
21.如图1,在正方形中,点E在上(不与点B,C重合),点F在边上,,连接交于点M.
(1)求证:;
(2)如图2,连接与交于点G,连接交于点H.
①求证:;
②当时,求的值;
(3)如图3,若E是的中点,以点B为圆心,为半径作,P是上的一个动点,连接交于点N,则的最大值为 .
22.如图1,在中,点D是边上的中点.、分别垂直射线于点E、F.
(1)求证:;
(2)求证:;
(3)如图2,在矩形中,为直径的半圆O上有一个动点P,连接、.利用图1中得到的结论:探求的最小值是多少.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D D A B A A C B A A
题号 11 12
答案 A A
1.D
【分析】作于,根据菱形的性质可判断为等边三角形,则,,再利用勾股定理计算出,再利用点与圆的位置关系得到当点在上时,的值最小,即可求出.
【详解】作于,如图,
菱形的边,,
为等边三角形,
,,
,
,
在中,
.
梯形沿直线折叠,A的对应点,
点 在以点为圆心,为半径的弧上,
当点在上时,的值最小,此时,
∵,
,
,
故选:D.
【点睛】本题考查了菱形的性质,折叠的性质,圆的基本性质,解决本题的关键是确定点在上时,的值最小.
2.D
【分析】本题考查了点和圆的位置关系,熟悉点和圆的位置关系的判断是关键.根据点到圆心的距离和圆的半径之间的数量关系,即可判断点和圆的位置关系.点到圆心的距离小于圆的半径,则点在圆内;点到圆心的距离等于圆心的半径,则点在圆上;点到圆心的距离大于圆的半径,则点在圆外.
【详解】解:的半径为,点在外,
,
故选:D.
3.A
【分析】根据P为⊙O外一点,若点P到⊙O的最短距离为3,最长距离为7,可以得到圆的直径,从而可以求得圆的半径.
【详解】解:∵P为⊙O外一点,若点P到⊙O的最短距离为3,最长距离为7,
∴⊙O的直径为:7-3=4,
∴⊙O的半径为2,
故选:A.
【点睛】本题考查点和圆的位置关系,解题的关键是明确题意,找出所求问题需要的条件.
4.B
【分析】先根据勾股定理算出点到圆心的距离,再利用点与圆的位置关系进行判断:到圆心的距离等于半径的点必在圆上、到圆心的距离小于半径的点必在圆内、到圆心的距离大于半径的点必在圆外.
【详解】解:A.到圆心的距离,点在内,故选项错误;
B.到圆心的距离,点在上,故选项正确;
C.到圆心的距离,点在外,故选项错误;
D.到圆心的距离,点在外,故选项错误.
故选:B
【点睛】本题考查了点与圆的位置关系以及数量关系、勾股定理,用数量关系来判断位置关系,典型的数形结合.
5.A
【分析】根据点和圆的位置与圆的半径的关系求得的范围即可解答.
【详解】解:∵的半径为4,点在内,
∴,
选项中只有3符合题意,
故选:A.
【点睛】本题考查了点和圆的位置关系,熟知点和圆的位置与圆的半径的关系是解答的关键.
6.A
【分析】由题意可得点在以点为圆心,为半径的上,在轴的负半轴上取点,连接,分别过、作,,垂足为、,先证,得,从而当取得最大值时,取得最大值,结合图形可知当,,三点共线,且点在线段上时,取得最大值,然后分别证,,利用相似三角形的性质即可求解.
【详解】解:∵点为平面内一动点,,
∴点在以点为圆心,为半径的上,
在轴的负半轴上取点,连接,分别过、作,,垂足为、,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴当取得最大值时,取得最大值,结合图形可知当,,三点共线,且点在线段上时,取得最大值,
∵,,
∴,
∴,
∵,
∴,
∵轴轴,,
∴,
∵,
∴,
∴即,
解得,
同理可得,,
∴即,
解得,
∴,
∴当线段取最大值时,点的坐标是,
故选A.
【点睛】本题主要考查了勾股定理、相似三角形的判定及性质、圆的一般概念以及坐标与图形,熟练掌握相似三角形的判定及性质是解题的关键.
7.C
【分析】利用点到圆心的距离与圆的半径之间的大小关系,进行判断即可.
【详解】解:∵的直径为4cm,
∴的半径为2cm,
∵点P到圆心O的距离为3cm,大于的半径,
∴点P在外;
故选C.
【点睛】本题考查点与圆的位置关系.熟练掌握利用点到圆心的距离与圆的半径之间的大小关系,来判断点与圆之间的位置关系,是解题的关键.
8.B
【分析】本题应分为两种情况来讨论,关键是得出:当点P在⊙O内时,直径=最近点的距离+最远点的距离;当点P在⊙O外时,直径=最远点的距离-最近点的距离.
【详解】解:点应分为位于圆的内部与外部两种情况讨论:
①如图,当点在圆内时,最近点的距离为,最远点的距离为,
则直径是,
∴半径是;
②如图,当点在圆外时,最近点的距离为,最远点的距离为,
则直径是,
∴半径是.
故选.
【点睛】本题考查了点与圆的位置关系,在解答此题时注意到分两种情况进行讨论是解决本题的关键.
9.A
【分析】根据⊙O的半径为r和点P到圆心的距离OP=d的大小关系判断即可.
【详解】解:∵⊙O的半径为5,点P到圆心O的距离为4,
而4<5,
∴点P在⊙O内,
故选:A.
【点睛】本题考查的是点与圆的位置关系,设⊙O的半径为r,点P到圆心的距离OP=d,则有:①点P在圆外 d>r;②点P在圆上 d=r;①点P在圆内 d<r.
10.A
【分析】首先利用勾股定理求得直角三角形斜边的长,然后求得点E与点B的距离,从而求得第E与圆B的位置关系.
【详解】解:在Rt△ABC中,∠C=90°,AC=4,BC=3,
由勾股定理得到:,
∵E为AB的中点,
∴BE=AB=2.5.
∵BC=3,
∴BE<BC,
∴点E在⊙B的内部,
故选:A.
【点睛】本题主要考查了勾股定理,点与圆的位置关系,直角三角形斜边上的中线,根据点到圆心的距离和圆的半径之间的数量关系,来判断点和圆的位置关系.
11.A
【分析】本题考查点与圆的位置的关系.比较点到圆心的距离与半径的大小关系,即可得出结果.
【详解】解:∵的半径为8cm,点P到圆心的距离为7cm,,
∴P在内;
故选A.
12.A
【分析】本题考查点与圆的位置关系.若圆半径为r,点到圆心的距离为d,则有:当时,点在圆外;当时,点在圆上,当时,点在圆内.判断圆的半径与大小即可解答.
【详解】解:∵的半径,点P到圆心O的距离,
∴,
∴点P在上.
故选:A
13. 3
【分析】(1)当点P在线段AB上时,AP的长度有最小值,即可求解;
(2)由“SAS”可证△PAB△AD,可得D=PB=1,点的运动路线为以D为圆心,以1为半径的圆上,则当在对角线BD上时,B最小,再利用勾股定理求对角线BD的长,则得出B的长.
【详解】解:(1)∵点P在⊙B上移动,
∴当点P在线段AB上时,AP的长度有最小值,
最小值=AB﹣PB=4﹣1=3,
故答案为:3.
(2)如图,连接BP,
由旋转得:AP=A,∠PA=90°,
∴∠PAB+∠BA=90°,
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴∠BA+∠DA=90°,
∴∠PAB=∠DA,
在△AD和△PAB中,
∴△AD△PAB(SAS),
∴D=PB=1,
∴点P在以点D为圆心,D为半径的圆上,
∴当在对角线BD上时,B最小,
在Rt△ABD中,∵AB=AD=4,
∴BD===,
∴B=BD﹣D=﹣1,
即B长度的最小值为﹣1.
故答案为:﹣1.
【点睛】本题主要考查了正方形的性质,圆的性质,全等三角形的判定及性质,解题的关键是找出线段的最小值1.
14.2π
【分析】首先根据圆的面积公式,求出圆的半径是多少;然后根据圆的周长公式,求出这个圆的周长为多少即可.
【详解】解:设圆的半径是rcm,
则πr2=2π,
解得r=,
所以它的周长为: .
故答案为2π
【点睛】此题主要考查了算术平方根的性质和应用,要熟练掌握,解答此题的关键是要明确:如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做a的算术平方根.
15.2或6
【分析】根据已知条件能求出圆的直径,即可求出半径,此题点的位置不确定所以要分类讨论.
【详解】①当点在圆外时,
∵圆外一点和圆周的最短距离为4,最长距离为8,
∴圆的直径为8﹣4=4,
∴该圆的半径是2;
②当点在圆内时,
∵点到圆周的最短距离为4,最长距离为8,
∴圆的直径=8+4=12,
∴圆的半径为6,
故答案为2或6.
【点睛】本题考查了点和圆的位置关系的应用,能根据已知条件求出圆的直径是解此题的关键.
16./
【分析】因为,点为的中点,根据直角三角形斜边上中线的性质得出,所以是以为圆心,以为半径的圆弧上的点,作关于的对称点,连接,交于,交以为圆心,以为半径的圆于,此时的值最小,最小值为的长;根据勾股定理求得,即可求得,从而得出的最小值;
【详解】解:,点为的中点,
,
是以为圆心,以为半径的圆弧上的点,
作关于的对称点,连接,交于,交以为圆心,以为半径的圆于,此时的值最小,最小值为的长;
,
,,
,
,
;
的最小值为;
故答案为:.
【点睛】本题考查了轴对称最短路线问题,矩形的性质,勾股定理,点到圆上一点的距离,判断出点的位置是解题的关键.
17.在⊙A上
【分析】先根据两点间的距离公式计算出OA,然后根据点与圆的位置关系的判定方法判断点O与⊙A的位置关系.
【详解】解:∵点A的坐标为(4,3),
∴OA==5,
∵半径为5,
∴OA=r,
∴点O在⊙A上.
故答案为:在⊙A上.
【点睛】本题考查了点与圆的位置关系:点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,当点P在圆外 d>r;当点P在圆上 d=r;当点P在圆内 d<r.
18.(1)乙,
(2)
(3)丙同学的结论错误;丁同学的说法正确.
【分析】(1)乙的方法:用表示,进而得到关于的解析式即可;
(2)分和两种情况,先求出的坐标,利用中点坐标公式,求出点坐标,根据点到圆上的距离求得的最小值,利用两点间的距离公式,求出的最小值,即可得解;
(3)①利用(1)中小远的方法,求出点的轨迹,进行判断即可.
【详解】(1)解:乙的方法更严谨,
令,,
∴,
∴,
∴点运动轨迹的函数表达式为;
故答案为:乙,;
(2)解:∵,,
∴,,
∴移动到点的位置需要的时间为:秒,
①当时,,
,,
则:;
②当时,,
∴,,即:
则:;
综上:,
令,,消去,得的运动轨迹的函数表达式为,
当时,,
∴,
∵
∴点在以为圆心,为半径的圆上,
∴的值最小值为,
(3)①∵,
令,则:;
∴,
∴点的轨迹为抛物线;
∵,令,则:,
∴;
∴点的轨迹为直线;则丙同学的结论错误
联立,整理,得:,
∵,
∴方程没有实数根,即抛物线和直线没有交点,
即点在运动过程中不可能重合,丁同学的说法正确.
【点睛】本题考查坐标与图形,二次函数和一次函数的综合应用.熟练掌握两点间的距离公式,中点坐标公式,正确的求出函数的解析式,利用二次函数的性质进行求解,是解题的关键.
19.(1)见解析;(2),Q(0,3)
【分析】(1)连结BO并且延长交圆于C1,连结AO并且延长交圆于C2,即可求解;
(2)根据“智慧三角形”的定义可得△OPQ为直角三角形,根据题意可得一条直角边为1,当斜边最短时,另一条直角边最短,则面积取得最小值,由垂线段最短可得斜边最短为3,从而得到点Q坐标,再根据勾股定理可求另一条直角边即PQ长.
【详解】解:(1)如图所示,过直径做△ABC即可;
(2)如图所示:
由“智慧三角形”的定义可得△OPQ为直角三角形,
根据题意可得一条直角边OP=1,
∴PQ最小时,△POQ的面积最小,
根据勾股定理可知,当斜边OQ最短时,PQ最小,面积取得最小值,
由垂线段最短可得斜边最短为3,即OQ=3,
∴Q(0,3),
由勾股定理可得PQ==,
∴当面积取得最小值时,点Q的坐标为(0,3),PQ的长为.
【点睛】本题考查了圆与勾股定理的综合应用,掌握圆的相关知识,熟练应用勾股定理,明确“智慧三角形”的定义是解题的关键.
20.(1);(2)
【分析】(1)由点E是的中点及折叠的性质可知,进而可得以E为圆心、以为半径的经过点A、P.用勾股定理解求出,当E、P、D三点共线时,可取最小值,,由此可解;
(2)作点E关于的对称点,连接交于点,交于点,连接,,在四边形中,,当O、M、N、四点共线时,此时最小,最小值为的长度.
【详解】解:(1)由点E是的中点及折叠的性质可知:,且点F是的角平分线与的交点.
∴以E为圆心、以为半径的经过点A、P.
∵点E是中点,,
.
在中,由勾股定理得,即,
.
由图可知:当E、P、D三点共线时,可取最小值,
,
长的最小值为.
(2)作点E关于的对称点,连接交于点,交于点,连接,,在四边形中,,当O、M、N、四点共线时,此时最小,最小值为的长度.
,由对称可知,,
.
由题意可得,
.
在中,由勾股定理得:,即,
,
,
的最小值为.
【点睛】本题考查折叠的性质,圆的基本性质,线段的最值问题,勾股定理,正确作出辅助线是解题的关键.
21.(1)见解析
(2)①见解析;②
(3)2
【分析】(1)证明,则,利用互余关系即可证明;
(2)①证明,则,再由(1)的证明即可证明;
②分别过G、H作的垂线,垂足分别为K、Q;设,则可得,则可得,由相似三角形的性质得,进而得,则由勾股定理可分别求得,从而求得结果;
(3)延长交于点W,过P作于Y,过P作交射线于点J;易证,则,从而,当最大时,最大;证明,则可得,当最大时,最大,此时点P与点W重合,Y与M重合;由面积关系求出,则可得的值,最后求得结果;
【详解】(1)证明:四边形是正方形,
,
,
,
,
,
,
即,
;
(2)①证明:四边形是正方形,
,
,
,
,
再由(1)的证明知:,
,
即;
②解:如图,分别过G、H作的垂线,垂足分别为K、Q;
则;
∵四边形为正方形,
,
,
,
设,
由①知,,
,
,
;
,
,
,
,
即,
;
,
,
,
即,
由勾股定理得:,;
,
,
,
又由(1)知,,
由勾股定理得,
;
(3)解:如图,延长交于点W,过P作于Y,过P作交射线于点J;
,
,
,
,
则当最大时,最大;
,,
,
;
,
,
;
∵点E是的中点,,
,
由勾股定理得,
,
即,
上式表明:当最大时,最大,从而最大;
此时点P与点W重合,Y与M重合;
,
,
则,
,
的最大值为;
故答案为:2.
【点睛】本题是正方形的综合,考查了正方形的性质,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,等腰三角形的判定与性质,圆上点到切线的距离最大为直径等知识,综合性较强,构造适当的辅助线,灵活运用相关知识是解题的关键.
22.(1)见详解;(2)见详解;(3)的最小值为388
【分析】(1)由题意易得,,然后可证,则问题可证;
(2)由图1及勾股定理可得:,,,进而可得,,然后根据线段的和差关系可得,,两式相加即可得证;
(3)取AB的中点F,连接PF,由(2)中结论可得:,由题意易得,要使为最小,只需满足PF的值为最小,根据圆外的点到圆上的点的最值问题可得当点O、P、F三点共线时,PF可取最小值,连接OF,交⊙O于点P,过点O作OH⊥AB于点H,进而可得,然后问题可求解.
【详解】(1)证明:∵,
∴,
∵点D是边上的中点,
∴,
∵,
∴(AAS),
∴;
(2)由图1及勾股定理可得:
,,,
由(1)可得:,,
∴,,
∵,
∴,,
∴
=,
=
=
=,
∴;
(3)取AB的中点F,连接PF,如图所示:
由(2)中结论可得:,
∵,DE是⊙O的直径,
∴,
∴,
要使为最小,只需满足PF的值为最小,根据圆外的点到圆上的点的最值问题可得当点O、P、F三点共线时,PF可取最小值,连接OF,交⊙O于点P,过点O作OH⊥AB于点H,如图所示:
∴,,
∴,
∴,
∴PF的最小值为,
∴的最小值为.
【点睛】本题主要考查圆的最值问题及勾股定理,熟练掌握圆的最值问题及勾股定理是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
