4.8图形的位似同步练习（含解析）

中小学教育资源及组卷应用平台
4.8图形的位似
学校:___________姓名：___________班级：___________考号：___________
一、单选题
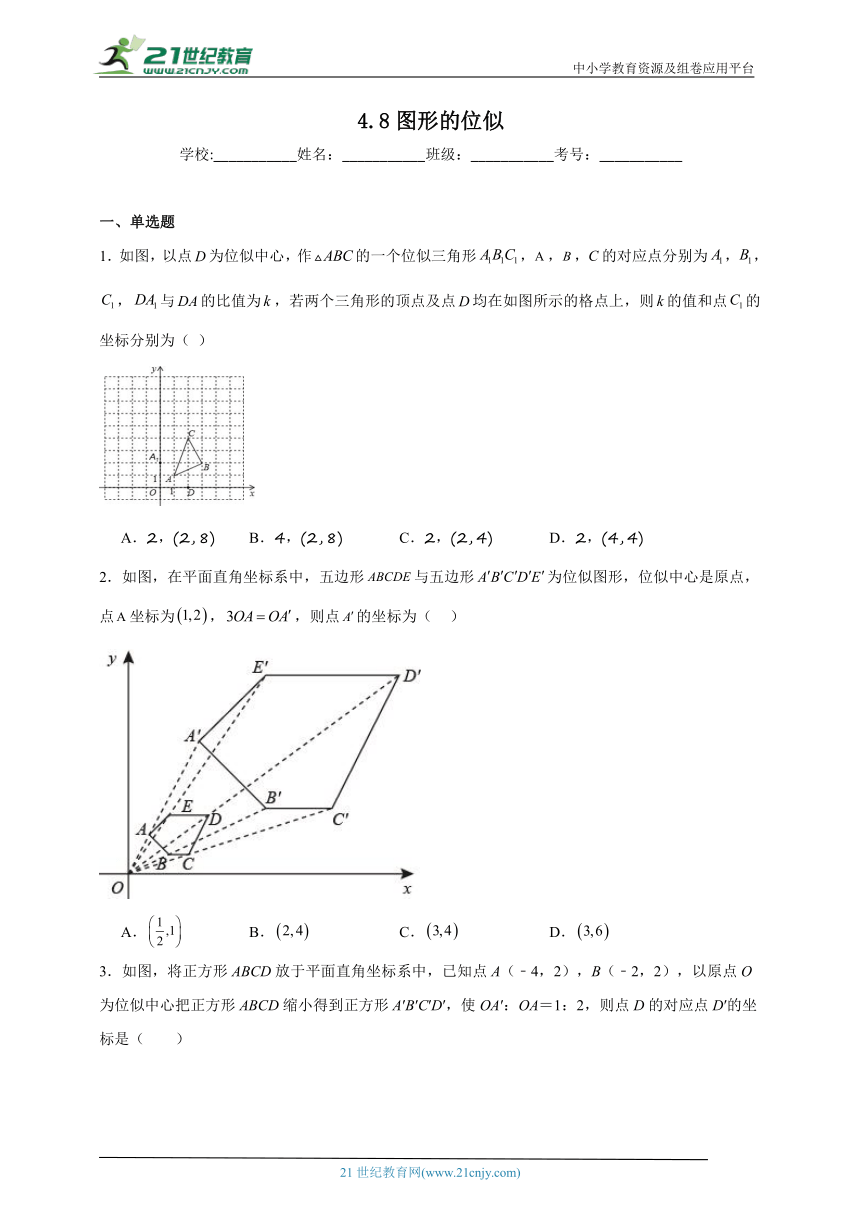
1．如图，以点为位似中心，作的一个位似三角形，，，的对应点分别为，，，与的比值为，若两个三角形的顶点及点均在如图所示的格点上，则的值和点的坐标分别为（ ）
A．2，(2, 8) B．4，(2, 8) C．2，(2, 4) D．2，(4, 4)
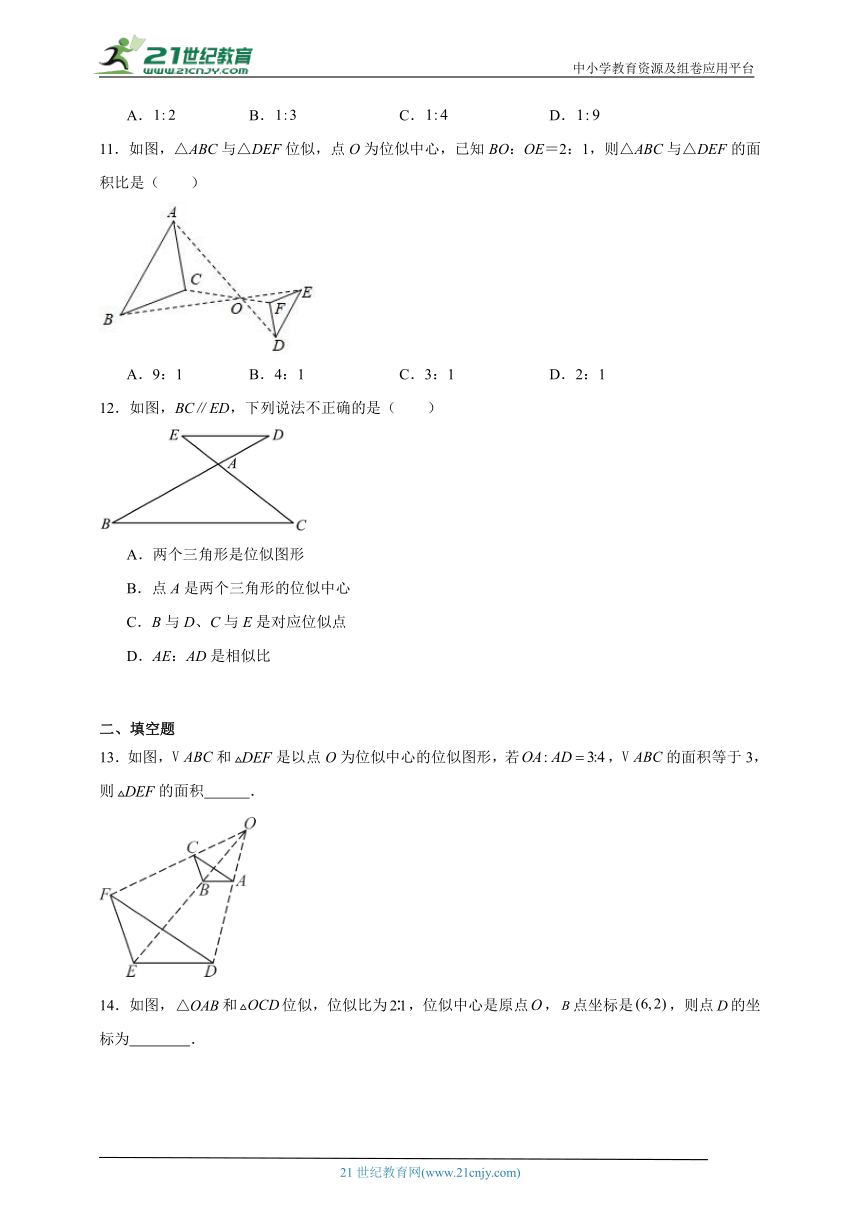
2．如图，在平面直角坐标系中，五边形与五边形为位似图形，位似中心是原点，点坐标为，，则点的坐标为（ ）
A． B． C． D．
3．如图，将正方形ABCD放于平面直角坐标系中，已知点A（﹣4，2），B（﹣2，2），以原点O为位似中心把正方形ABCD缩小得到正方形A′B′C′D′，使OA′：OA＝1：2，则点D的对应点D′的坐标是（　　）
A．（﹣8，8） B．（﹣8，8）或（8，﹣8）
C．（﹣2，2） D．（﹣2，2）或（2，﹣2）
4．如图，以点为位似中心，作四边形的位似图形，已知，若四边形的面积是4，则四边形面积是（ ）
A．6 B．9 C．16 D．18
5．如图，以点O为位似中心，把的各边长放大为原来的2倍得到，以下说法中错误的是（ ）

A． B．点A，O，三点在同一条直线上
C． D．
6．下列3个图形中是位似图形的有( )
A．1个 B．2个 C．3个 D．0个
7．如图，在平面直角坐标系中，以原点O为位似中心，若A点坐标为，C点坐标为，，则线段长为（　　）
A．2 B．4 C． D．
8．2022年2月4日，第二十四届冬季奥林匹克运动会在北京隆重开幕．此次冬奥会会徽是以汉字“冬”为灵感来源设计的．在下面的四个图中，能由下图经过平移得到的是（ ）
A． B． C． D．
9．如图中的两个三角形是位似图形，点的坐标为，则它们位似中心的坐标是（ ）
A． B． C． D．
10．如图，与位似，点O是它们的位似中心，其中位似比为，则与的面积之比是（ ）
A． B． C． D．
11．如图，△ABC与△DEF位似，点O为位似中心，已知BO：OE＝2：1，则△ABC与△DEF的面积比是（　　）
A．9：1 B．4：1 C．3：1 D．2：1
12．如图，BC∥ED，下列说法不正确的是（　　）
A．两个三角形是位似图形
B．点A是两个三角形的位似中心
C．B与D、C与E是对应位似点
D．AE：AD是相似比
二、填空题
13．如图，和是以点O为位似中心的位似图形，若，的面积等于3，则的面积 ．

14．如图，和位似，位似比为，位似中心是原点，点坐标是，则点的坐标为 ．
15．如图，△ABC与△DEF位似，点O为位似中心，OA＝AD，则△ABC与△DEF的面积比为 ．
16．如图，已知与位似，位似中心为点，且的面积与的面积比为，则的比值为
17．平面坐标系中，点P（3，4）是线段AB上一点，以原点为位似中心把△AOB扩大到原来的2倍，则点P对应的点的坐标是 ．
三、解答题
18．如图，与是位似图形．
(1)在网格中建立平面直角坐标系，使得点A的坐标为，点的坐标为，则点B的坐标为______．
(2)以点A为位似中心，在网格图中作，使和位似，且位似比是1∶2；
(3)在图上标出与的位似中心P，并写出点P的坐标为______，计算四边形的周长为______．
19．如图，在边长为1个单位长度的小正方形组成的网格中，建立如图所示的平面直角坐标系，并给出了格点△ABC（顶点为网格线的交点）．
（1）若△A1B1C1与△ABC以点O为对称中心对称，画出△A1B1C1．
（2）若△A2B2C2，与△ABC以点O为位似中心位似，A2B2＝2AB，在第四象限，画出△A2B2C2．
20．综合与实践
主题：某数学实践小组以标准对数视力表为例，探索视力表中的数学知识
操作：步骤一：用硬纸板复制视力表中视力为0.1，0.2所对应的“E”，并依次编号为①，②，垂直放在水平桌面上，开口的底部与桌面的接触点为，；
步骤二：如1图所示，将②号“E”沿水平桌面向右移动，直至从观测点O看去，对应顶点，与点O在一条直线上为止．
结论：这时我们说，在处用①号“E”测得的视力与在处用②号“E”测得的视力相同．
探究：（1）①如1图，与之间存在什么关系？请说明理由；
②由标准视力表中的，，可计算出时，___________mm；
运用：（2）如果将视力表中的两个“E”放在如2图所示的平面直角坐标系中，两个“E”字是位似图形，位似中心为点O，①号“E”与②号“E”的相似比为，点P与点Q为一组对应点．若点Q的坐标为，则点P的坐标为___________．
21．（1）【操作体验】用一张矩形纸片折等边三角形．
第一步，对折矩形纸片（）（图），使与重合，得到折痕，把纸片展平（图②）．
第二步，如图③，再一次折叠纸片，使点落在上的处，并使折痕经过点，得到折痕，折出，，得到．
请证明是等边三角形．
（2）【数学思考】
如图④，小明画出了图③的矩形和等边三角形．他发现，在矩形中把经过图形变化，可以得到图⑤中的更大的等边三角形．请描述图形变化的过程．
（3）【问题解决】
已知矩形一边长为，另一边长为．对于每一个确定的的值，在矩形中都能画出最大的等边三角形．请画出不同情形的示意图，并写出对应的的取值范围．
22．若绕点逆时针旋转后，与构成位似图形，则我们称与互为“旋转位似图形”．

(1)知识理解：
如图①，与互为“旋转位似图形”．
①若，，，则 ；
②若，，，则 ；
(2)知识运用：
如图②，在四边形中，，于点，，求证：与互为“旋转位似图形”；
(3)拓展提高：
如图③，为等边三角形，点为的中点，点是边上的一点，点为延长线上的一点，点在线段上，，且与互为“旋转位似图形”．若，，求．
参考答案：
题号 1 2 3 4 5 6 7 8 9 10
答案 A D D B A B C B A D
题号 11 12
答案 B D
1．A
【分析】利用勾股定理求出DA1与DA的值，然后相比即可求出k值；连接DB并延长至B1，使DB1=2DB，连接DC并延长至C1，使DC1=2DC，然后顺次连接A1，B1，C1，然后根据平面直角坐标系写出点C1的坐标即可得解．
【详解】根据勾股定理DA=，
DA1=，
∴k==2，
C1的坐标为（2，8）．
故选A．
【点睛】本题考查了利用位似变换作图，以及位似变换的性质，位似比的求解，是基础题，找出对应点的位置是解题的关键．
2．D
【分析】根据题意得到位似比，从而求得点的坐标；
【详解】解：
∵五边形与五边形为位似图形，位似中心是原点，
∴得到位似比为
又∵点坐标为
∴，
故选：D
【点睛】本题考查了位似图形的性质，熟练掌握位似比的性质是解题的关键．
3．D
【分析】根据如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或﹣k进行解答．
【详解】∵点A（﹣4，2），B（﹣2，2），以原点O为位似中心把正方形ABCD缩小得到正方形A′B′C′D′，使OA′：OA＝1：2，
∴点D的坐标是：（﹣4，4），
∴点D的对应点D′的坐标是：（﹣2，2）或（2，﹣2）．
故选D．
【点睛】本题考查位似变换：位似图形与坐标，在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或﹣k．
4．B
【分析】本题主要考查了位似图形的性质．根据位似图形的性质可得，即可求解．
【详解】解：∵四边形和四边形是位似图形，
∴，
∵，
∴，
∵四边形的面积是4，
∴四边形面积是9．
故选：B
5．A
【分析】根据位似的性质对各选项进行判断后即可解答．
【详解】∵点O为位似中心，把△ABC中放大到原来的2倍得到△A'B'C'，
∴，，，点A，O，三点在同一条直线上．
∴，
综上，只有选项A错误，符合题意．
故选A．
【点睛】本题考查了位似变换：如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形，这个点叫做位似中心．位似的性质：两个图形必须是相似形；对应点的连线都经过同一点；对应边平行（或共线）．
6．B
【详解】由位似图形的定义：“如果两个图形不仅是相似图形，而且每组对应点的连线交于一点，对应边互相平行或在一条直线上，那么这两个图形叫做位似图形”分析可知，上面3个图形中，第1个和第3个图形是位似图形，第2个图形不是位似图形，即3个图形中位似图形有2个.
故选B.
7．C
【分析】
根据题意求出位似比，根据位似比计算即可．
【详解】
解：∵以原点O为位似中心，A点坐标为，C点坐标为，
∴线段与线段的位似比为，
∵，
∴，
故选：C．
【点睛】
本题考查的是位似变换的概念和性质，根据题意求出位似比是解题的关键．
8．B
【分析】根据轴对称得到A，根据平移得到B，根据旋转得到C，根据位似得到D．
【详解】解：A．是通过轴对称看得到，故选项A不正确，不符合题意；
B．通过平移可以得到，故选项B正确，符合题意；
C．通过旋转可以得到，故选项C不正确，不符合题意；
D．通过缩小位似变换看得到，故选项D不正确，不符合题意；
故选B．
【点睛】本题考查四种变换，掌握轴对称变换，平移变换，旋转变换，位似变换是解题关键．
9．A
【分析】根据位似图形的概念作出位似中心，根据坐标与图形性质解答．
【详解】解：如图，点O为两个三角形的位似中心，
∵点M的坐标为（3，2），
∴位似中心O的坐标为（0，2），
故选：A．
【点睛】本题考查的是位似变换、坐标与图形性质，掌握位似图形的对应顶点的连线相交于一点是解题的关键．
10．D
【分析】本题考查的是位似变换的概念、相似三角形的性质，掌握相似三角形的面积比等于相似比的平方是解题的关键．根据位似图形的概念得到，根据相似三角形的面积比等于相似比的平方计算，得到答案．
【详解】解：与位似，其中位似比为，
与的面积之比为，
故选：D．
11．B
【分析】根据位似图形的位似比等于相似比，相似相似三角形的面积比等于相似比的平方，进而得到答案．
【详解】△ABC与△DEF位似，
BO：OE＝2：1，
故选：B．
【点睛】本题考查的是位似图形的概念和性质，掌握位似图形的概念、相似三角形的面积比等于相似比的平方是解题的关键．
12．D
【分析】根据位似变换的概念判断即可．
【详解】解：A、∵BC∥ED，
∴△ADE∽△ABC，
∵△ADE与△ABC对应点的连线相交于一点，对应边平行或在同一条直线上，
∴△ADE与△ABC是位似图形，本选项说法正确，不符合题意；
B、点A是两个三角形的位似中心，本选项说法正确，不符合题意；
C、B与D、C与E是对应位似点，本选项说法正确，不符合题意；
D、AE：AD不是相似比，AE：AC是相似比，本选项说法错误，符合题意；
故选：D．
【点睛】本题考查的是位似变换的概念，两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形，这个点叫做位似中心．
13．/
【分析】本题考查的是位似变换，相似三角形的判定和性质．根据位似变换的概念得到，，从而得到得到，根据相似三角形的性质求出，再根据相似三角形的性质计算即可．
【详解】解：∵，
∴，
∵和是以点O为位似中心的位似图形，
∴，，
∴，
∴，
∴，
∵的面积等于3，
∴的面积为．
故答案为：
14．
【分析】本题主要考查了位似变换，直接利用位似图形的性质得出对应点坐标．
【详解】解：∵和位似，位似中心是原点O，和的相似比为，B点坐标是，
∴点D的坐标为：即．
故答案为：．
15．1：4
【分析】根据位似图形的概念得到△ABC∽△DEF，根据相似三角形的性质求出，根据相似三角形的面积比等于相似比的平方求解即可．
【详解】解：∵△ABC与△DEF位似，
∴△ABC∽△DEF，，
∴△OAB∽△ODE，
∴＝＝，
∴△ABC与△DEF的面积比＝（）2＝，
故答案为：1：4．
【点睛】本题考查了位似，相似知识．解题的关键在于求出相似比．
16．
【分析】
本题考查了位似变换：位似图形必须是相似形，位似图形对应点的连线都经过同一点；对应边平行或共线．
利用位似性质得到，，进而可解答．
【详解】解：∵与位似，位似中心为点O，
∴，
∴，
∵的面积与面积之比为，
∴，
∴．
故答案为：．
17．（6，8）或（﹣6，﹣8）．
【分析】根据位似变换的性质计算即可．
【详解】点P（3，4）是线段AB上一点，以原点O为位似中心把△AOB放大到原来的两倍，
则点P的对应点的坐标为（3×2，4×2）或（3×（﹣2），4×（﹣2）），即（6，8）或（﹣6，﹣8），
故答案为（6，8）或（﹣6，﹣8）．
【点睛】本题考查的是位似变换、坐标与图形的性质，在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或﹣k．
18．(1)
(2)见解析
(3)，
【分析】（1）根据题意找到原点以及坐标轴的位置，建立平面直角坐标系，进而求得点的坐标即可；
（2）根据题意找到的中点即可画出；
（3）连接交于点，则点即为所求，根据坐标系写出点的坐标即可，根据网格的特点以及勾股定理求得四边形的周长即可.
【详解】（1）如图，
点B的坐标为，
故答案为：；
（2）如图，
（3）如图，
点的坐标是，
的周长为：
，
故答案为：，.
【点睛】本题考查了平面直角坐标系，坐标与图形，画位似三角形，求位似中心，勾股定理，掌握以上知识是解题的关键．
19．（1）见解析；（2）见解析
【分析】（1）利用中心对称的性质作出的对应点,即可；
（2）利用位似变换的性质分别作出的对应点即可．
【详解】解：（1）如图，△A1B1C1即为所求；
（2）如图，△A2B2C2即为所求．
【点睛】本题考查了作图－位似变换，，中心对称，解题的关键是掌握位似变换，中心对称的性质，正确作出图形．
20．（1）①相等，见解析；②43.2；（2）
【分析】本题考查了相似三角形的的应用，位似的性质．
（1）①根据题意证明，从而得到，即可得到；②把，，，代入即可求解．
（2）根据位似比为，代入数据计算即可．
【详解】解：（1）①．
由题意得，
∴，
∴，
，
；
②，，，，
．
．
故答案为：．
（2）①号“E”与②号“E”的相似比为，点P与点Q为一组对应点．若点Q的坐标为，
点P的坐标为，即，
故答案为：．
21．（1）见解析；（2）见解析；（3）见解析
【分析】（1）由折叠的性质和垂直平分线的性质得出，，得出即可；
（2）由旋转的性质和位似的性质即可得出答案；
（3）由等边三角形的性质、直角三角形的性质、勾股定理进行计算，画出图形即可；
【详解】解：（1）由折叠的性质得：是的垂直平分线，是的垂直平分线，
，，
，
是等边三角形．
（2）以点为中心，在矩形中把逆时针方向旋转适当的角度，
得到；
再以点为位似中心，将放大，使点的对应点落在上，得到；
如图⑤所示；
（3）矩形的一边长为，等边三角形边上的高为边长的倍，根据题意，如图所示（答案不唯一）
【点睛】本题考查了等边三角形的性质与判定，旋转的性质，位似的性质，勾股定理，掌握以上知识是解题的关键．
22．(1)①27°；②
(2)见解析
(3)
【分析】（1）①依据和互为“旋转位似图形”，可得，依据相似三角形的对应角相等，即可得到；
②依据，可得，根据，，，即可得出；
（2）依据，即可得到，进而得到，再根据，，即可得到，进而得出和互为“旋转位似图形”；
（3）利用直角三角形的性质和勾股定理解答即可．
【详解】（1）①和互为“旋转位似图形”，
，
，
又，，
；
②，
，
，，，
，
，
故答案为：；；
（2），，
，
，即，
又，
，
，
又，，
，
，
，
绕点逆时针旋转的度数后与构成位似图形，
和互为“旋转位似图形”；
（3）点为的中点，
，
由题意得：，
，
，
，
，
由勾股定理可得，
，
．
【点睛】本题是相似形综合题，主要考查了相似三角形的判定及性质，等腰直角三角形的判定及性质，勾股定理的综合运用．在解答时添加辅助线等腰直角三角形，利用相似形的对应边成比例是关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)