第五章投影与视图同步练习（含解析）

中小学教育资源及组卷应用平台
第五章投影与视图
学校:___________姓名：___________班级：___________考号：___________
一、单选题
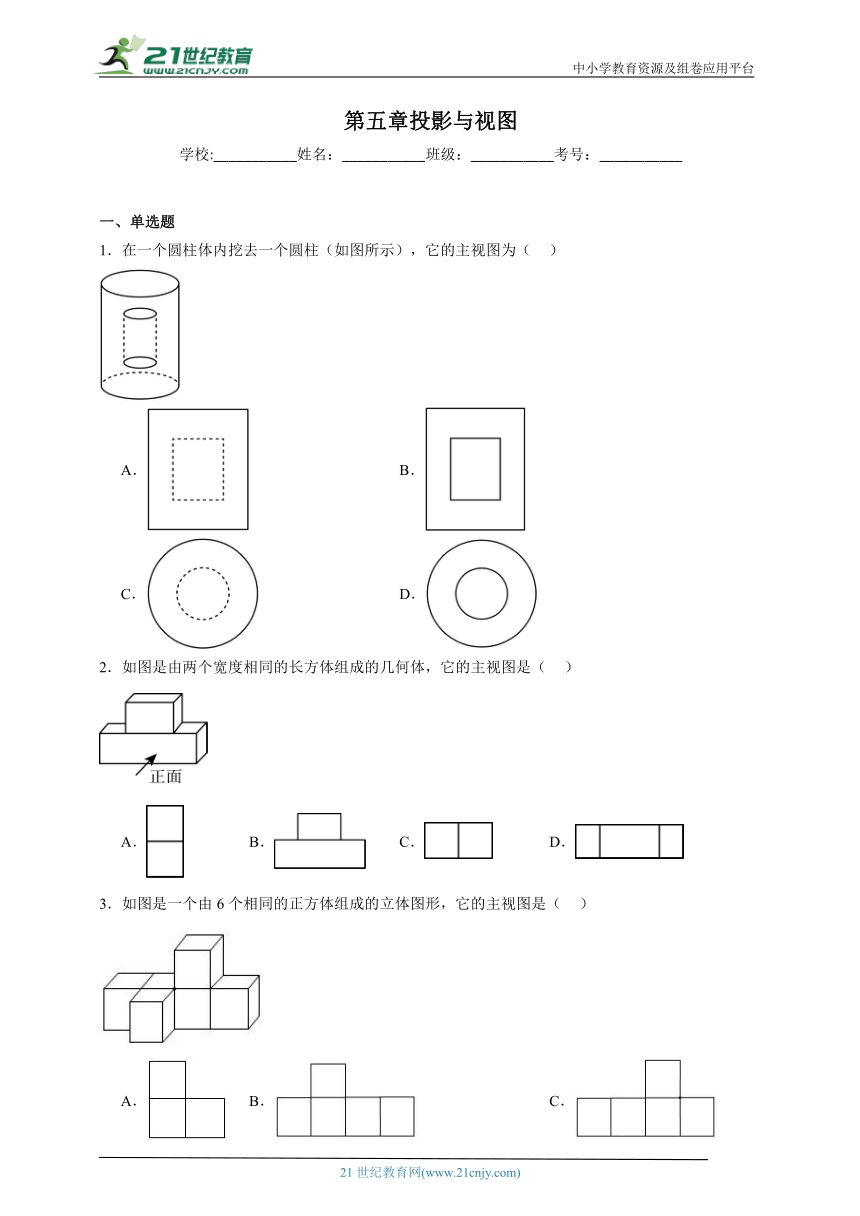
1．在一个圆柱体内挖去一个圆柱（如图所示），它的主视图为（ ）

A． B．
C． D．
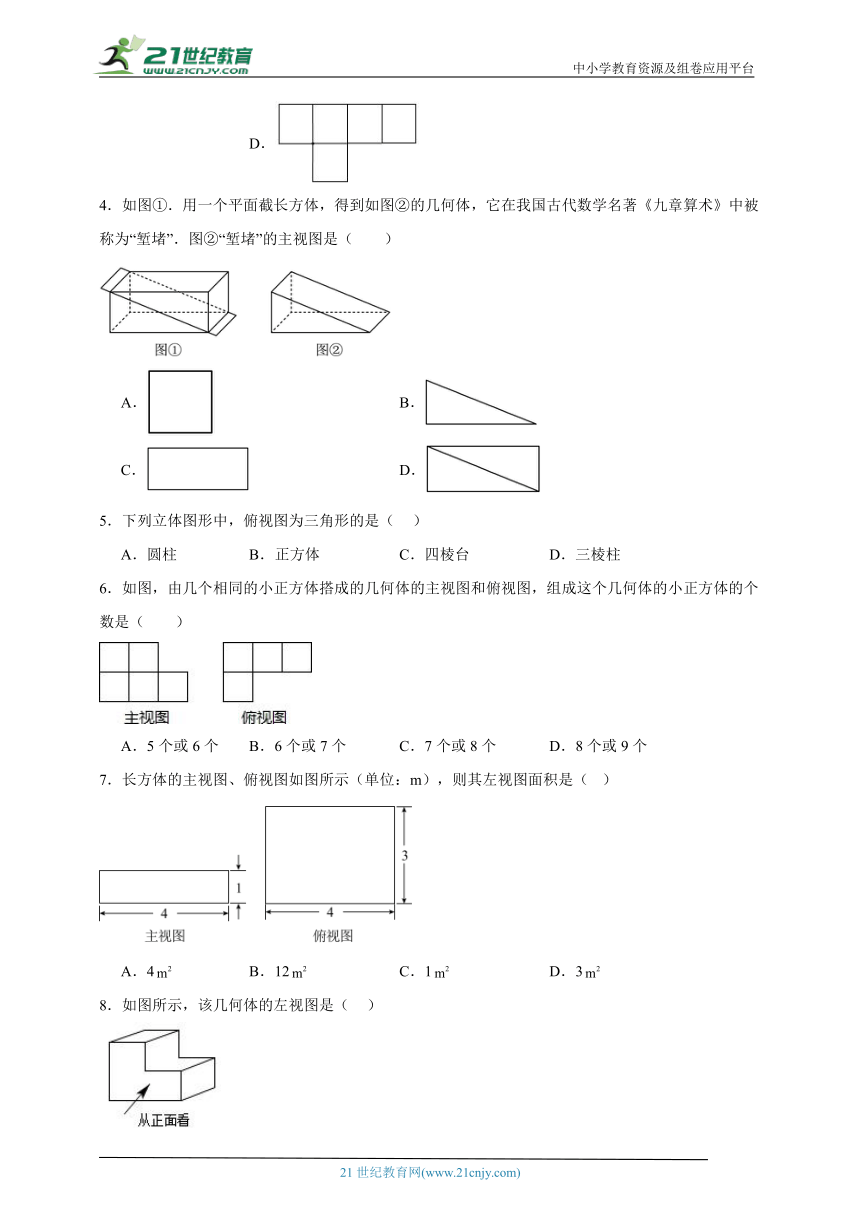
2．如图是由两个宽度相同的长方体组成的几何体，它的主视图是（ ）
A． B． C． D．
3．如图是一个由6个相同的正方体组成的立体图形，它的主视图是（ ）
A． B． C． D．
4．如图①．用一个平面截长方体，得到如图②的几何体，它在我国古代数学名著《九章算术》中被称为“堑堵”．图②“堑堵”的主视图是（　　）
A． B．
C． D．
5．下列立体图形中，俯视图为三角形的是（ ）
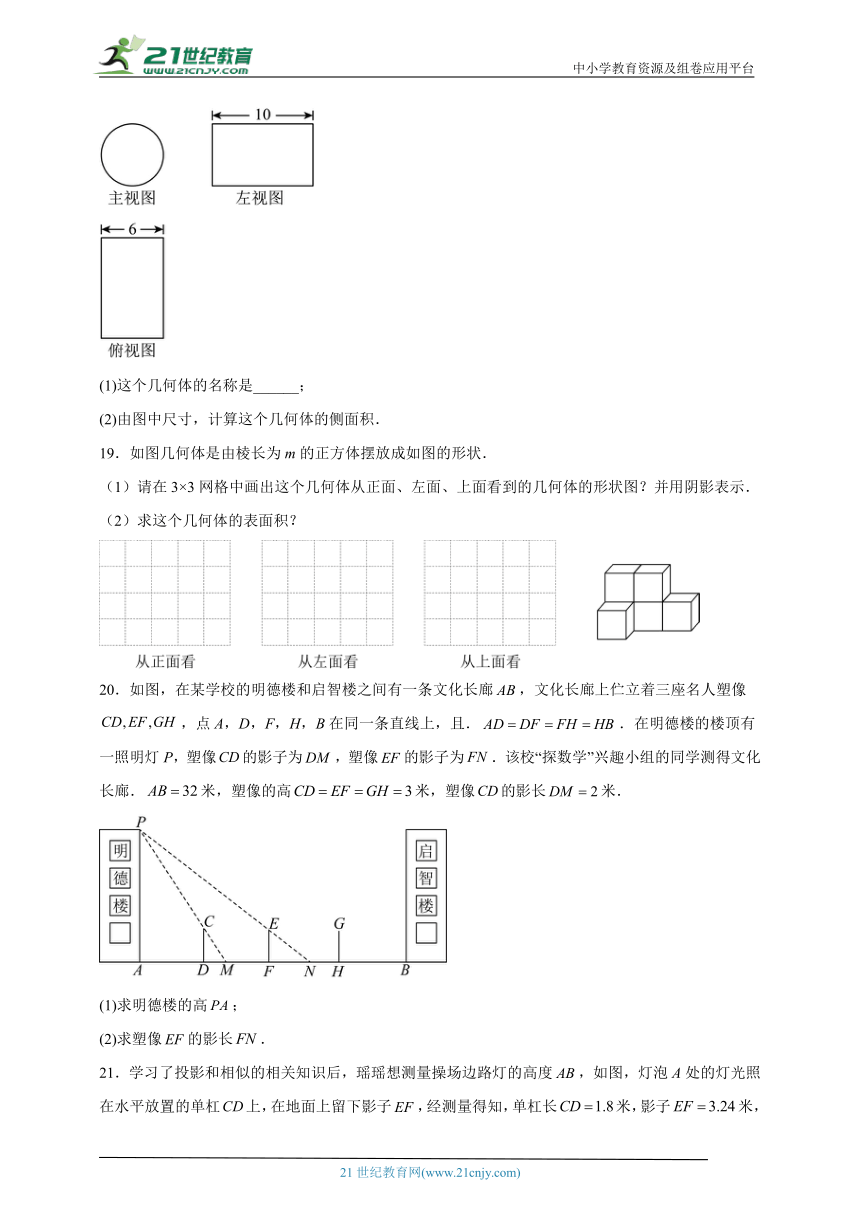
A．圆柱 B．正方体 C．四棱台 D．三棱柱
6．如图，由几个相同的小正方体搭成的几何体的主视图和俯视图，组成这个几何体的小正方体的个数是（　　）
A．5个或6个 B．6个或7个 C．7个或8个 D．8个或9个
7．长方体的主视图、俯视图如图所示（单位：m），则其左视图面积是（ ）
A．4 B．12 C．1 D．3
8．如图所示，该几何体的左视图是（ ）
A． B． C． D．
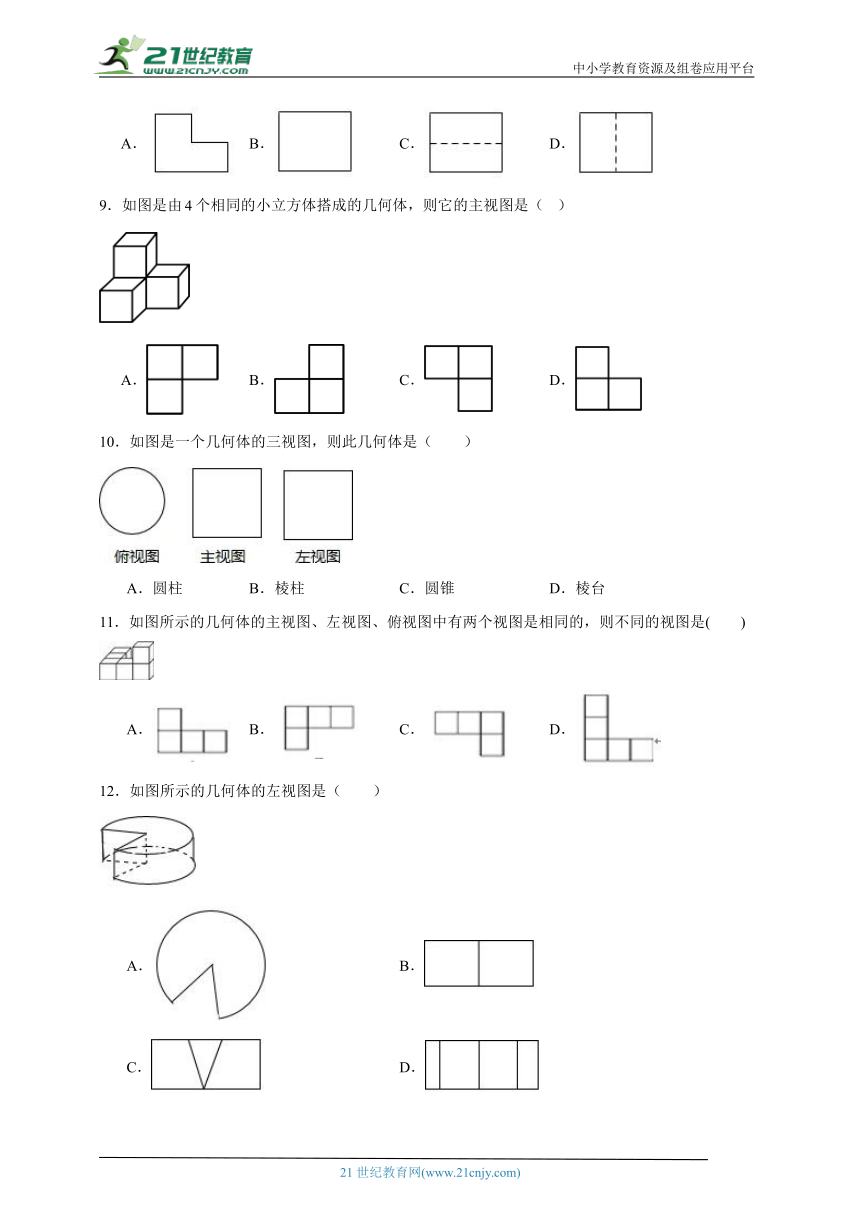
9．如图是由个相同的小立方体搭成的几何体，则它的主视图是（ ）
A． B． C． D．
10．如图是一个几何体的三视图，则此几何体是（　　）
A．圆柱 B．棱柱 C．圆锥 D．棱台
11．如图所示的几何体的主视图、左视图、俯视图中有两个视图是相同的，则不同的视图是(　　)
A． B． C． D．
12．如图所示的几何体的左视图是（　　）
A． B．
C． D．
二、填空题
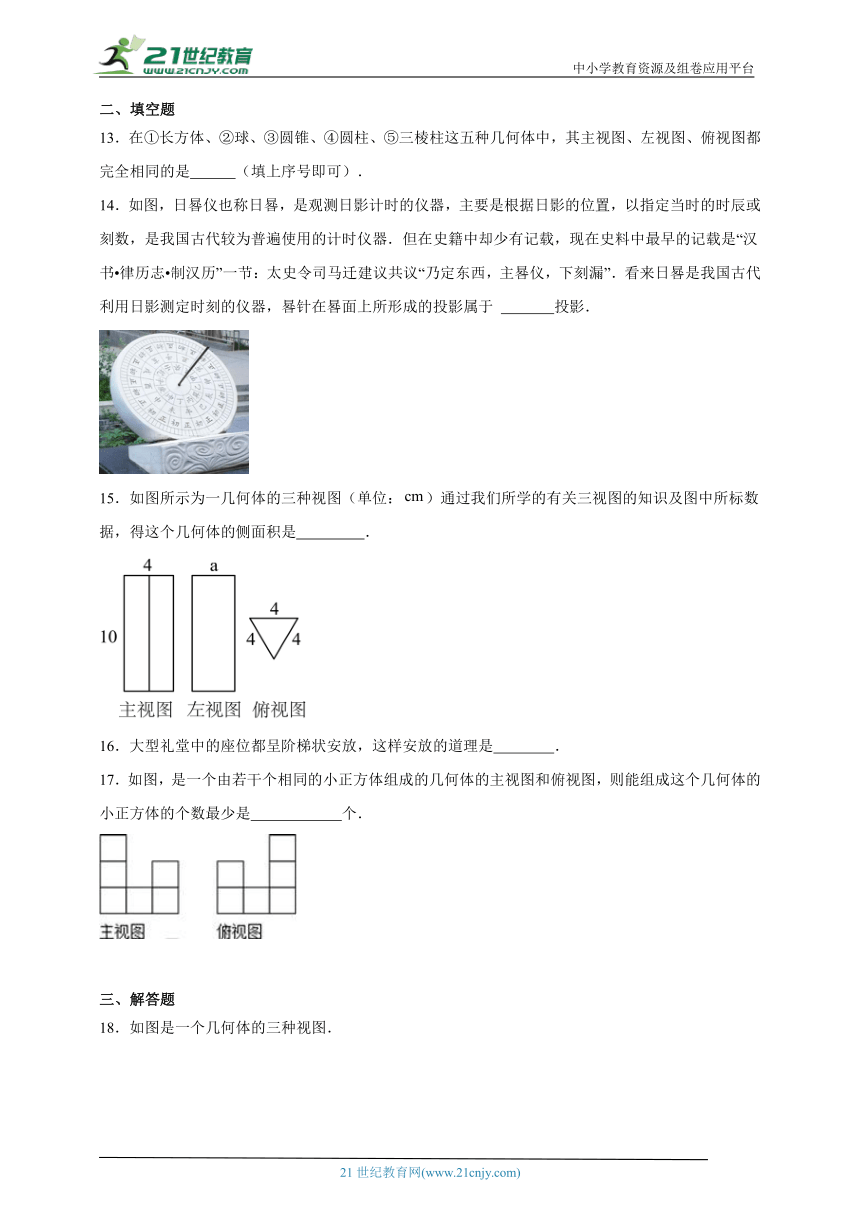
13．在①长方体、②球、③圆锥、④圆柱、⑤三棱柱这五种几何体中，其主视图、左视图、俯视图都完全相同的是 （填上序号即可）．
14．如图，日晷仪也称日晷，是观测日影计时的仪器，主要是根据日影的位置，以指定当时的时辰或刻数，是我国古代较为普遍使用的计时仪器．但在史籍中却少有记载，现在史料中最早的记载是“汉书 律历志 制汉历”一节：太史令司马迁建议共议“乃定东西，主晷仪，下刻漏”．看来日晷是我国古代利用日影测定时刻的仪器，晷针在晷面上所形成的投影属于 投影．
15．如图所示为一几何体的三种视图（单位：）通过我们所学的有关三视图的知识及图中所标数据，得这个几何体的侧面积是 ．
16．大型礼堂中的座位都呈阶梯状安放，这样安放的道理是 ．
17．如图，是一个由若干个相同的小正方体组成的几何体的主视图和俯视图，则能组成这个几何体的小正方体的个数最少是 个．
三、解答题
18．如图是一个几何体的三种视图．

(1)这个几何体的名称是______；
(2)由图中尺寸，计算这个几何体的侧面积．
19．如图几何体是由棱长为m的正方体摆放成如图的形状．
（1）请在3×3网格中画出这个几何体从正面、左面、上面看到的几何体的形状图？并用阴影表示．
（2）求这个几何体的表面积？
20．如图，在某学校的明德楼和启智楼之间有一条文化长廊，文化长廊上伫立着三座名人塑像，点A，D，F，H，B在同一条直线上，且．．在明德楼的楼顶有一照明灯P，塑像的影子为，塑像的影子为．该校“探数学”兴趣小组的同学测得文化长廊．米，塑像的高米，塑像的影长米．
(1)求明德楼的高；
(2)求塑像的影长．
21．学习了投影和相似的相关知识后，瑶瑶想测量操场边路灯的高度，如图，灯泡A处的灯光照在水平放置的单杠上，在地面上留下影子，经测量得知，单杠长米，影子米，单杠高米．已知，，，点B、M、E、N、F在同一水平直线上．
(1)请你在图中画出点F的位置；（保留画图痕迹）
(2)请你求出路灯的高度．
22．如图，学习完投影后，小光同学在灯光下观察自己的影子．线段表示小光站立的位置，线段表示此时操场上的灯杆，点为路灯所在位置．
(1)画出小光在路灯C照明下的投影示意图，并记作；
(2)如果小光身高，他站在距离灯杆为的处时，测得自己的影长，求灯杆的高度．
23．如图所示，△ABC被平行光线照射，CD⊥AB于D，AB在投影面上．
(1)指出图中AC的投影是什么？CD与BC的投影呢？
(2)探究：当△ABC为直角三角形(∠ACB＝90°)时，易得AC2＝AD·AB，此时有如下结论：直角三角形一直角边的平方等于它在斜边射影与斜边的乘积，这一结论我们称为射影定理．通过上述结论的推理，请证明以下两个结论．
①BC2＝BD·AB；②CD2＝AD·BD．
24．操作与研究：如图，被平行于的光线照射，于D，在投影面上．
(1)指出图中线段的投影是______，线段的投影是______．
(2)问题情景：如图1，中，，，我们可以利用与相似证明，这个结论我们称之为射影定理，请证明这个定理．
(3)【结论运用】如图2，正方形的边长为15，点O是对角线的交点，点E在上，过点C作，垂足为F，连接，
①试利用射影定理证明；
②若，求的长．
参考答案：
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C B D B D C D A
题号 11 12
答案 D D
1．A
【分析】本题考查了几何图形的三视图，根据主视图是从正面看得到的图形，以及看到到的轮廓线用实线表示，看不见的轮廓线用虚线表示，对图形进行判断，即可解题．
【详解】解：主视图是从正面看得到的图形，观察已知几何体，可知其主视图是一个长方形，中间看不见的轮廓线用虚线表示，
它的主视图为 ，
故选：A．
2．B
【分析】本题考查了三视图的知识，熟知主视图是从物体的正面看到的视图是解题的关键．按照主视图的定义逐项判断即可．
【详解】解：从正面看该几何体，下面是一个大长方形，上面叠着一个小长方形，
故选：B．
3．C
【分析】画出从正面看到的图形即可得到它的主视图．
【详解】解：从正面看有2层，底层是四个小正方形，上层从左数第三个是一个小正方形，故C符合题意，
故选：C．
【点睛】本题考查了简单组合体的三视图：画简单组合体的三视图要循序渐进，通过仔细观察和想象，再画它的三视图．
4．B
【分析】根据几何体的主视图是从正面所看到的图形进行判断即可得出答案．
【详解】解：图②“堑堵”的主视图如图所示：
故选：B．
【点睛】本题主要考查几何体的主视图，理解主视图的概念是解答的关键．
5．D
【分析】本题考查了几何体的三种视图．俯视图是从物体上面看所得到的图形，据此判断得出物体的俯视图．
【详解】解：A、圆柱体的俯视图是圆，故此选项不符合题意；
B、正方体的俯视图是正方形，故此选项不符合题意；
C、四棱台的俯视图是正方形，故此选项不符合题意；
D、三棱柱的俯视图是三角形，故此选项符合题意；
故选：D．
6．B
【分析】从俯视图中可以看出最底层小正方体的个数及形状，从主视图可以看出每一层小正方体的层数和个数，从而算出总的个数．
【详解】解：从俯视图可得最底层有4个个小正方体，由主视图可得上面一层是2个或3小正方体，
则组成这个几何体的小正方体的个数是6个或7个；
故选：B．
【点睛】本题考查三视图的知识及从不同方向观察物体的能力，解题中用到了观察法．确定该几何体有几列以及每列方块的个数是解题关键．
7．D
【分析】根据长方体的主视图、俯视图都是矩形；主视图和俯视图所看的长相等，左视图和俯视图所看的宽度相同，左视图和主视图所看的高相同，所以左视图矩形的高是1，宽是3，从而求得左视图的面积．
【详解】解：∵长方体的主视图、俯视图都是长方形；主视图和俯视图所看的长相等，左视图和俯视图所看的宽度相同，左视图和主视图所看的高相同，
∴左视图的高是1，宽是3，
∴左视图的面积是，
故选D．
【点睛】本题考查了长方体的三视图，熟练掌握几何体的三视图中，主视图和俯视图所看的长相等，左视图和俯视图所看的宽度相同，左视图和主视图所看的高相同是解题的关键．
8．C
【分析】根据左视图是从左面看到的图形判定则可．
【详解】解：从左边看，是一个长方形，长方形的中间有一条横向的虚线．
故选：C．
【点睛】本题考查简单组合体的三视图，正确掌握观察角度是解题关键．
9．D
【详解】解：从正面看，底层有个正方形，上层左边有个正方形．
故选：D．
【点睛】本题主要考查了简单组合体的三视图的知识，掌握主视图是指从物体的正面看物体是解答本题的关键．
10．A
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．
【详解】由于主视图和左视图为正方形可得此几何体为柱体，由俯视图为圆形可得为圆柱．
故选A．
【点睛】本题主要考查了学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查.
11．D
【详解】试题分析：几何体的左视图和主视图是相同的，则不同的视图是俯视图，俯视图是D选项所给的图形．故选D．
12．D
【分析】根据左视图即从左边观察得到的图形可得．
【详解】解：从左边观察，可得几何体的左视图是：
故选D．
【点睛】本题考查三视图的知识，左视图是从物体的左面看得到的视图，主要考查了学生的空间想象能力．
13．②
【分析】分析每个几何体的三视图，最后得出答案．
【详解】解：①长方体主视图是长方形、左视图是长方形、俯视图是长方形，②球的三视图是大小相同的圆，所以主视图、左视图、俯视图都完全相同的是②球．①长方体和③圆锥、④圆柱、⑤三棱柱的三视图都不完全相同．
故答案为：②．
【点睛】本题比较容易，考查三视图和考查立体图形的三视图和学生的空间想象能力．
14．平行
【分析】本题考查了平行投影．熟练掌握平行投影的定义是解题的关键．
根据平行投影的定义进行判断作答即可．
【详解】解：因为太阳光属于平行光线，而日晷利用日影测定时刻，所以晷针在晷面上所形成的投影属于平行投影．
故答案为：平行．
15．
【分析】本题考查了求几何体的侧面积以及几何体的三视图，先由三视图得出这个几何体是正三棱柱，结合侧面积等于三个长方形的面积之和，即，据此作答．
【详解】解：依题意，这个几何体是正三棱柱
∴
∴这个几何体的侧面积是
故答案为：
16．减小盲区
【分析】大型礼堂中为了后排观众能有更好的观看效果，而将前后排座位安排成阶梯状，是为了增大视角，减少盲区，可据此进行判断．
【详解】解：大型礼堂中的座位都呈阶梯状安放，可以增加后排观众的视角，减少盲区，以便得到更好的观看效果.
故答案为减小盲区．
【点睛】此题考查视角、盲区的相关知识，利用数学知识解决实际问题是中学数学的重要内容．
17．9
【分析】易得这个几何体共有3层，由俯视图可得第一层正方体的个数，由主视图可得第二层和第三层正方体的可能的最少个数，相加即可．
【详解】解：由俯视图易得最底层有6个正方体，由主视图第二层最少有2个正方体，第三层最少有1个正方体，那么共有9个正方体组成．
故答案为：9．
【点睛】本题考查俯视图小正方形的个数即为最底层的小正方体的个数，主视图第二层和第三层小正方形的个数即为其余层数小正方体的最少个数．
18．(1)圆柱
(2)
【分析】本题考查了由三视图判断几何体，解题的关键是掌握常见几何体的三视图及圆柱的侧面积公式．
（1）根据俯视图和左视图可以判断出该几何体是柱体，根据主视图判断为圆柱；
（2）根据圆柱的底面直径和高，再利用圆柱的侧面积公式计算即可；
【详解】（1）解：根据三视图即可得出该几何体是圆柱，
故答案为：圆柱．
（2）由图可知，圆柱的底面圆的直径是6，高为10，
则圆柱的侧面积为：．
所以这个几何体的侧面积为．
19．（1）答案见解析；（2）24m2
【分析】（1）根据三视图的定义，画出图形即可；
（2）根据三视图确定表面有多少个正方形即可解决问题.
【详解】（1）三视图如图所示：
（2）这个几何体的表面一共有2（5+3+4）=24个正方形，
∴这个几何体的表面积=24m2．
【点睛】本题考查作图-三视图，解题的关键是理解题意，正确作出三视图．
20．(1)15米；
(2)4米．
【分析】本题考查了相似三角形的应用，中心投影，熟练掌握相似三角形的判定与性质是解题的关键．
（1）根据已知易得米，证明，从而利用相似三角形的性质可解答；
（2）根据题意可得，证明，从而利用相似三角形的性质进行计算即可解答．
【详解】（1）∵，米，
米．
由题意，得．
∵，
∴，
解得．
答：明德楼的高为15米．
（2）由题意，得．
∵，
∴，
解得．
答：塑像的影长为4米．
21．(1)见解析
(2)
【分析】本题主要考查了相似三角形的判定与性质，灵活运用相似三角形的判定与性质成为解题的关键．
（1）如图：连接并延长交延长线于F，即可确定点F的位置；
（2）先证明，根据相似三角形的性质可得，再证明得到，最后代入数据求得的长即可．
【详解】（1）解：点F的位置如图所示．
（2）解：由题意得：，
，，
，
，
．
，，
，
，即，
，即路灯的高度为．
22．(1)见解析
(2)．
【分析】本题考查了相似三角形的应用，熟记相似三角形的判定与性质是解题的关键．
（1）连接并延长交直线于点E，线段即为所作；
（2）根据相似三角形的判定与性质得出，代入数据求出的长即可．
【详解】（1）如图，
（2）由题意可知，，
，
，
，
．
答：灯杆的高度为．
23．(1)AC的投影是AD，CD的投影是点D，BC的投影是BD；(2)证明见解析.
【详解】试题分析：（1）在平行投影中，投影线垂直于投影面产生的投影叫做正投影，根据正投影的定义求解即可；
（2）①，结合两角对应相等的两三角形相似，可得△BCD∽△BAC，根据相似三角形对应边成比例可证明结论；
②同理可证△ACD∽△CBD，根据相似三角形对应边成比例可证明结论成立．
试题解析：
解：（1）∵CD⊥AB，
而平行光线垂直AB，
∴AC的投影是AD，CD的投影是点D，BC的投影为BD；
（2）①∵∠ACB＝90°，CD⊥AB于D，
∴∠ACB＝∠CDB＝90°．
∵∠B＝∠B，
∴△BCD∽△BAC，
∴，
∴BC2＝BD AB；
②同理可得：△ACD∽△CBD，
∴，
∴CD2＝AD BD．
点睛：本题考查了正投影的定义和相似三角形的判定与性质，熟记正投影的定义是解决（1）的关键，结合图形得出相似三角形是解决（2）的关键．
24．(1)，
(2)见解析；
(3)①见解析；②．
【分析】（1）根据题意，即可解答；
（2）通过证明得到，然后利用比例性质即可得到；
（3）①根据射影定理得，，则，即，加上，于是可根据相似三角形的判定得到结论；
（2）②先计算出，，，再利用（1）中结论得到，代入数据即可求解．
【详解】（1）解：根据题意，图中线段的投影是，线段的投影是．
故答案为：，；
（2）证明：如图，
∵，，
∴，
而，
∴，
∴，
∴；
（3）①证明：如图，
∵四边形为正方形，
∴，，
∴，
∵，
∴，
∴，
即，
而，
∴；
②∵，
而，
∴，
在中，，
在中，，
∵，
∴，即，
∴．
【点睛】本题考查了相似三角形的判定与性质和正方形的性质．也考查了射影定理：直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项；每一条直角边是这条直角边在斜边上的射影和斜边的比例中项．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)