第一章特殊平行四边形同步练习(含解析)
文档属性
| 名称 | 第一章特殊平行四边形同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-15 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第一章特殊平行四边形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.分别顺次连接①等腰梯形;②矩形;③菱形;④对角线相等的四边形“各边中点所构成的四边形”中,为菱形的是( )
A.① B.② C.①②③ D.①②④
2.顺次连接对角线相等的四边形各边中点,所得四边形是( ).
A.矩形 B.平行四边形 C.菱形 D.正方形
3.如图,在正方形中,,延长到点,使,连接,动点从点出发以每秒1个单位长度的速度沿向终点运动.设点的运动时间为秒.当和全等时,的值为( )
A.3 B.5 C.7 D.3或7
4.如图,在平面直角坐标系xOy,四边形OABC为正方形,若点B(1,4),则点A的坐标为( )
A.(3,1) B. C. D.(4,1)
5.如图,在正方形ABCD中,点E,F分别在BC,CD边上,△AEF是等边三角形,对角线AC交EF于点G,下列结论:①;②;③AC垂直平分EF;④.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
6.如图,菱形中,.则的度数为( )
A. B. C. D.
7.如图,在矩形中,两条对角线与相交于点,,则的长为( )
A.4 B.8 C. D.
8.下列命题中的真命题是( )
A.有一组邻边相等的四边形是菱形 B.对角线相等的四边形是矩形
C.有一组对边平行的四边形是平行四边形 D.对角线相等的菱形是正方形
9.如图,在矩形中,,垂直平分于点E,则的长为( )
A. B. C.4 D.2
10.在正方形ABCD中,AD=6,点M在边DC上,连接AM,△ADM沿直线AM翻折后点D落到点N,过点N作NE⊥CD,垂足为点E.如图,如果ED=2EC,则DM=( )
A.4+3 B.3+3 C.9﹣3 D.6﹣3
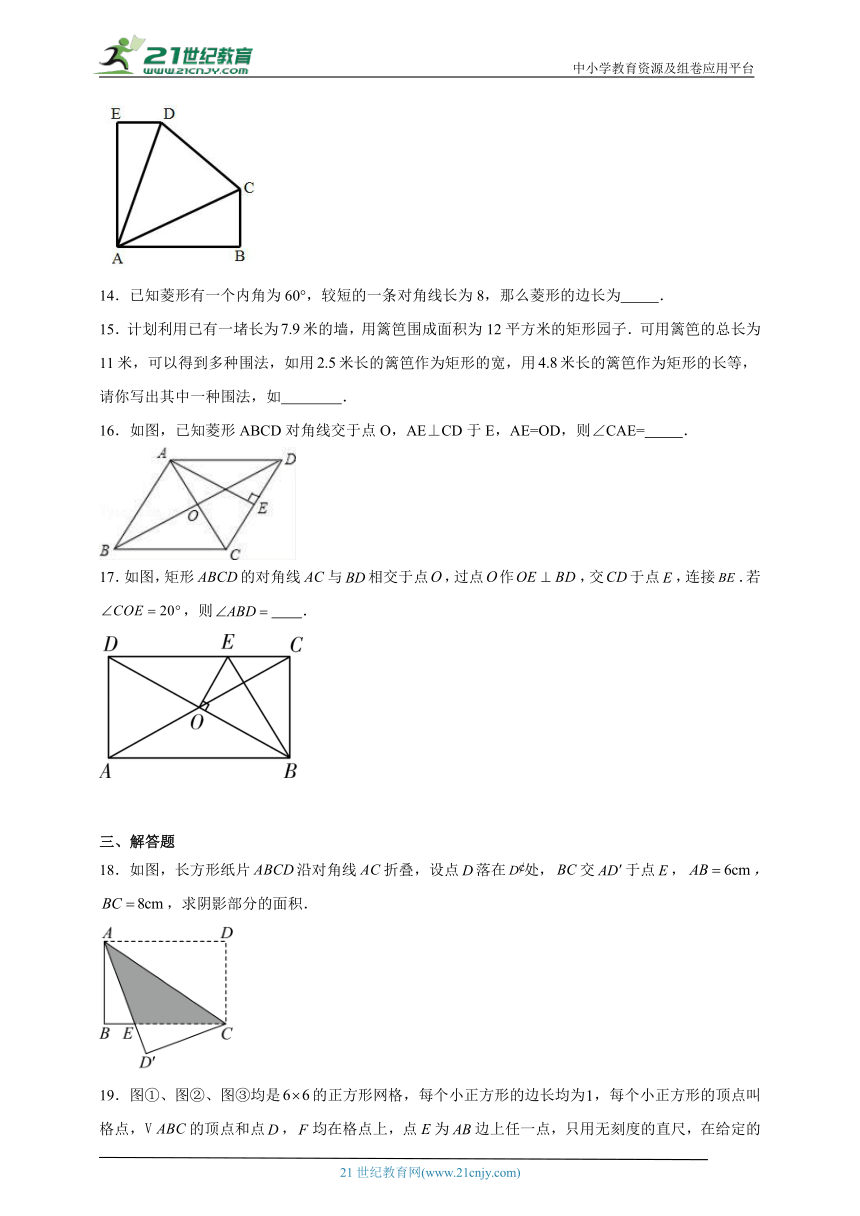
11.如图,E、F、M、N分别是正方形四条边上的点,,则四边形的形状是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
12.已知,如图,平行四边形的两条对角线交于点,设.其中:则满足( )
A. B. C. D.没有数量关系
二、填空题
13.如图,在五边形ABCDE 中,,,,点 A 到直线CD 的距离为
14.已知菱形有一个内角为60°,较短的一条对角线长为8,那么菱形的边长为 .
15.计划利用已有一堵长为米的墙,用篱笆围成面积为12平方米的矩形园子.可用篱笆的总长为11米,可以得到多种围法,如用米长的篱笆作为矩形的宽,用米长的篱笆作为矩形的长等,请你写出其中一种围法,如 .
16.如图,已知菱形ABCD对角线交于点O,AE⊥CD于E,AE=OD,则∠CAE= .
17.如图,矩形的对角线与相交于点,过点作,交于点,连接.若,则 .
三、解答题
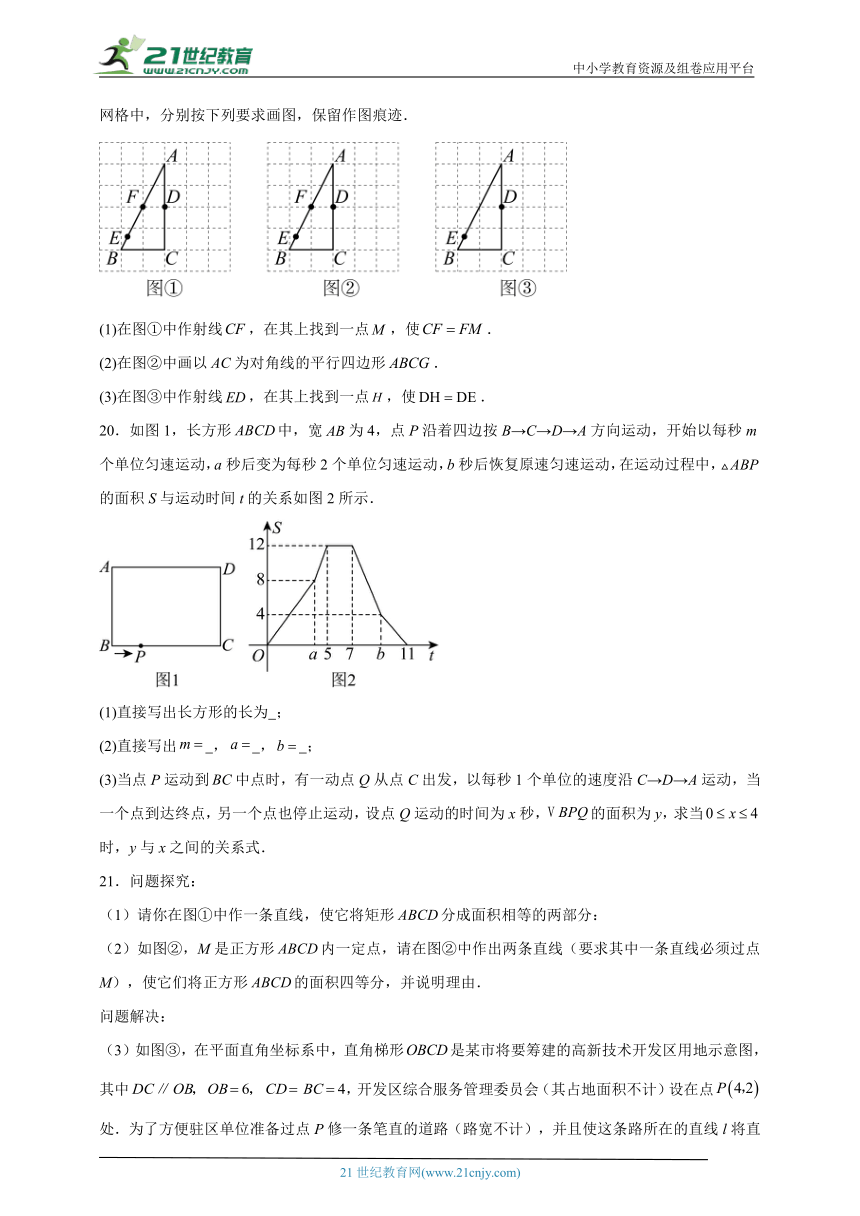
18.如图,长方形纸片沿对角线折叠,设点落在处,交于点,,,求阴影部分的面积.
19.图①、图②、图③均是的正方形网格,每个小正方形的边长均为,每个小正方形的顶点叫格点,的顶点和点,均在格点上,点E为边上任一点,只用无刻度的直尺,在给定的网格中,分别按下列要求画图,保留作图痕迹.
(1)在图①中作射线,在其上找到一点,使.
(2)在图②中画以为对角线的平行四边形.
(3)在图③中作射线,在其上找到一点,使.
20.如图1,长方形中,宽为4,点P沿着四边按B→C→D→A方向运动,开始以每秒m个单位匀速运动,a秒后变为每秒2个单位匀速运动,b秒后恢复原速匀速运动,在运动过程中,的面积S与运动时间t的关系如图2所示.
(1)直接写出长方形的长为 ;
(2)直接写出 , , ;
(3)当点P运动到中点时,有一动点Q从点C出发,以每秒1个单位的速度沿C→D→A运动,当一个点到达终点,另一个点也停止运动,设点Q运动的时间为x秒,的面积为y,求当时,y与x之间的关系式.
21.问题探究:
(1)请你在图①中作一条直线,使它将矩形分成面积相等的两部分:
(2)如图②,M是正方形内一定点,请在图②中作出两条直线(要求其中一条直线必须过点M),使它们将正方形的面积四等分,并说明理由.
问题解决:
(3)如图③,在平面直角坐标系中,直角梯形是某市将要筹建的高新技术开发区用地示意图,其中,开发区综合服务管理委员会(其占地面积不计)设在点处.为了方便驻区单位准备过点P修一条笔直的道路(路宽不计),并且使这条路所在的直线l将直角梯形分成面积相等的两部分,你认为直线l是否存在?若存在,求出直线l的表达式;若不存在,请说明理由.
22.如图,某自动感应门的正上方处装着一个感应器,该感应器的有效感应范围不超过,当人体进入感应器的感应范围时,感应门就会自动打开.现已知感应器离地面的高度,一个身高的学生缓慢走到离门的地方时(,假设此时人体与地面垂直),该学生头顶距离感应器多少米?感应门会自动打开吗?
23.探究与证明(八下教材63页《丰富多彩的正方形》)
【课本再现】
(1)如图,正方形的对角线交于点O,点O又是正方形的一个顶点,而且这两个正方形的边长相等,无论正方形绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的 .
【类比迁移】
(2)如图,等腰三角形中,,D是斜边的中点,点D又是直角三角形的直角顶点,,绕点D转动,分别与交于M、N,若,请直接写出两个三角形重叠部分的面积 .
【探索发现】
(3)小刚发现(1)在转动过程中,若边能与边交于点E、F,线段都存在一定的数量关系,请写出数量关系式,并加以证明.
24.如图,在△ABC中,∠ACB=90°,D点是AB的中点,DE、DF分别是△BDC、△ADC的角平分线.
(1)求∠CFD的度数;
(2)求证:四边形FDEC是矩形.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D C D B C B D D B C
题号 11 12
答案 D C
1.D
【分析】根据三角形中位线定理,可得四边形ABCD是平行四边形,再根据菱形的判定,有一组邻边相等的平行四边形是菱形,只要保证四边形的对角线相等即可.
【详解】解:如图,四边形ABCD中,点E,F,G,H分别为AB,BC,CD,AD的中点,连接AC,BD,
∵点E,F,G,H分别为AB,BC,CD,AD的中点,
∴,,
∴,
∴四边形EFGH是平行四边形,
∴连接任意四边形的四边中点都是平行四边形,
当四边形ABCD是等腰梯形时,AC=BD,
∴EH=EF,
此时四边形EFGH是菱形;
当四边形ABCD是矩形时,AC=BD,
∴EH=EF,
此时四边形EFGH是菱形;
当四边形ABCD是菱形时,AC⊥BD,
∴EH⊥EF,
此时四边形EFGH是矩形;
当四边形ABCD的对角线相等时,AC=BD,
∴EH=EF,
此时四边形EFGH是菱形;
∴符合条件的有:①②④.
故选:D
【点睛】本题主要考查了菱形的判定,中点四边形,三角形中位线定理,熟练掌握三角形中位线定理,菱形的判定定理是解题的关键.
2.C
【分析】本题考查菱形的判定和三角形的中位线定理,根据三角形中位线定理得到,再由得到,据此可得四边形是菱形.
【详解】解:如图,E、F、G、H分别是四边形的边的中点,
连接,
根据三角形的中位线定理得,,
∵四边形的对角线相等,
∴,
∴,
∴四边形是菱形.
故选:C.
3.D
【分析】分两种情况,①当点P在BC边上时,②当点P在AD边上时,找出对应的边列式计算即可.
【详解】当点在边上时,在与中,
,
∴.
由题意得,
∴.
当点在上时,在与中,
,
∴,
由题意得,解得.
当点在上时,不满足条件.
∴当的值为3或7时,和全等.
故选D.
【点睛】本题考查的是正方形的性质和全等三角形的性质,能够分情况讨论是解题的关键.
4.B
【分析】过点B作BD⊥y轴于点D,过点A作AE⊥x轴点E,DB与EA的延长线交于点F,通过证明△BFA≌△AEO可得AF=OE,BF=AE;利用B(1,4),可得BD=1,EF=4;通过说明四边形ODFE为矩形,可得DF=OE.计算出线段OE,AE的长即可求得结论.
【详解】解:过点B作BD⊥y轴于点D,过点A作AE⊥x轴点E,DB与EA的延长线交于点F,如图,
∵BD⊥y轴,AE⊥x轴,OD⊥OE,
∴四边形ODFE为矩形,
∴EF=OD,DF=OE,
∵点B(1,4),
∴OD=4,BD=1,
∵四边形OABC为正方形,
∴OA=AB,∠BAO=90°,
∴∠OAE+∠BAF=90°,
∵AE⊥x轴,
∴∠OAE+∠AOE=90°,
∴∠BAF=∠AOE,
在△BAF和△AOE中,
,
∴△BAF≌△AOE(AAS),
∴BF=AE,AF=OE,
∴DF=AF=OE,
∴OE+AE=EF=4,OE﹣AE=BD=1,
∴OE=,AE=,
∴A(,).
故选:B.
【点睛】本题主要考查了正方形的性质,矩形的判定及性质,全等三角形的判定及性质以及坐标与图形,能利用“一线三垂直”构造三角形全等是解题的关键.
5.C
【分析】先根据正方形的性质可得,再根据等边三角形的性质可得,然后根据直角三角形全等的判定定理证出,根据全等三角形的性质即可判断①;先根据全等三角形的性质可得,再根据角的和差即可判断②;先根据角的和差可得,再根据等腰三角形的三线合一即可判断③;先根据等腰直角三角形的判定与性质可得,再利用勾股定理即可判断④.
【详解】解:四边形是正方形,
,
是等边三角形,
,
在和中,,
,
,结论①正确;
,结论②错误;
又,
,即,
垂直平分(等腰三角形的三线合一),结论③正确;
是等腰直角三角形,
,
由勾股定理得:,结论④正确;
综上,正确的结论有3个,
故选:C.
【点睛】本题考查了正方形的性质、等边三角形的性质、勾股定理、直角三角形全等的判定定理与性质等知识点,熟练掌握各判定定理与性质是解题关键.
6.B
【分析】证明,平分,可得,,求解,,从而可得答案.
【详解】解:∵菱形,
∴,平分,
∴,,
∵,
∴,,
∴,
∴,
故选B
【点睛】本题考查的是菱形的性质,平行线的性质,角平分线的定义,熟记的菱形的性质是解本题的关键.
7.D
【分析】利用矩形的性质可知对角线互相平分且,再利用勾股定理求解即可.
【详解】解:在矩形中,
故选D.
【点睛】本题主要考查矩形的性质及勾股定理,熟练掌握矩形的性质及勾股定理求直角边是解决本题的关键.
8.D
【分析】根据菱形、矩形、平行四边形、正方形的判定逐项判断即可.
【详解】解:A、是假命题,因为:有一组邻边相等的平行四边形是菱形;
B、是假命题,例如等腰梯形;
C、是假命题,例如梯形;
D、是真命题,符合正方形的判定定理,
故选:D.
【点睛】本题考查了判断命题真假,熟练掌握菱形、矩形、平行四边形、正方形的判定定理是解题的关键.
9.B
【分析】由矩形的性质和线段垂直平分线的性质可证是等边三角形,可得,即可求解.
【详解】解:∵四边形是矩形,
∴,,
∵垂直平分,
∴,
∴,
∴是等边三角形,
∴,
∴,
∴.
故选:B.
【点睛】本题考查了矩形的性质,线段垂直平分线的性质,等边三角形的判定和性质,直角三角形的性质,灵活运用这些性质解决问题是解题的关键.
10.C
【分析】过点N作NH⊥AD于H,先证明四边形NEDH为矩形,得到HD=NE,NH=DE,根据ED=2EC,ED+EC=CD=6,可以得到ED=HN=4,再利用勾股定理求出AH,即可得到NE的值,最后再直角三角形MNE中用勾股定理求解即可.
【详解】解:如图所示,过点N作NH⊥AD于H,
∵四边形ABCD是正方形,AD=6
∴AD=CD=6,∠D=90°,
∵NE⊥CD,NH⊥AD,
∴∠NED=∠NHD=∠NHA=90°,
∴四边形NEDH为矩形,
∴HD=NE,NH=DE,
∵ED=2EC,ED+EC=CD=6,
∴ED=HN=4,
由翻折的性质可得AD=AN=6,DM=MN
∴,
∴,
设DM=MN=x,则ME=4-x,
则,
∴,
解得,
∴,
故选C.
【点睛】本题主要考查了矩形的性质与判定,正方形的性质,折叠的性质,勾股定理,解题的关键在于能够熟练掌握相关知识进行求解.
11.D
【分析】根据正方形的四边相等,四个角都是,,得到,推出,,,全等,得到,,,推出四边形是菱形,根据,推出.得到,从而得出四边形是正方形.
【详解】解:四边形是正方形.
证明:∵四边形是正方形,
∴
∵,
∴.
∵,
∴.
∴,
∴四边形是菱形.
∵,,
∴.
∴.
∴四边形是正方形.
故选:D.
【点睛】本题主要考查了正方形,全等三角形等,熟练掌握正方形的判定和性质,全等三角形的判定和性质,是解题的关键.
12.C
【分析】根据平行四边形的性质,得到AO=,BO=,然后在△ABO中,利用三角形两边之和大于第三边,两边之差小于第三边得到.
【详解】∵四边形ABCD是平行四边形,AC=z,BD=y
∴AO=,BO=
在△ABO中,两边之和大于第三边,两边之差小于第三边,即:
故选:C
【点睛】本题考查平行四边形的性质和三角形三边的关系,解题关键是利用平行四边形的性质,将x、y、z转化到同一个三角形中去.
13.
【分析】延长ED与BC交于点F,作AH⊥DC于点H,先证明出四边形AEFB是正方形,然后将△ABC逆时针旋转90°得到△AEG,通过证明△GAD≌△CAD证明出AH=AE最终得出答案.
【详解】
如图,延长ED与BC交于点F,作AH⊥DC于点H,
∵,
∴四边形AEFB是矩形,
∵AB=AE,
∴四边形AEFB是正方形,
将△ABC逆时针旋转90°得到△AEG,如图所示,
则AG=AC,∠GAE=∠CAB,
∵,
∴∠CAB+∠DAE=45°,
∴∠GAD=∠GAE+∠DAE=45°,
∴∠GAD=∠CAD,
在△GAD与△CAD中,
∵GA=CA,∠GAD=∠CAD,AD=AD,
∴△GAD≌△CAD(SAS),
∴AH=AE=,
故答案为.
【点睛】本题主要考查了正方形与全等三角形的综合运用,熟练掌握相关概念是解题关键.
14.8
【分析】先画出图形,根据菱形的性质,可证得△ABC为等边三角形,据此即可解答.
【详解】解:由题意得,∠ABC=60°,AC=8,
∵四边形ABCD是菱形,
∴BA=BC,
∴△ABC是等边三角形,
∴AB=AC=8,
故答案为:8.
【点睛】本题考查了菱形的性质,等边三角形的判定与性质,解答本题的关键是熟练掌握菱形的性质.
15.长为时,宽为(答案不唯一)
【分析】本题考查了方程与不等式的应用,设园子的宽为,长为,根据题意列出方程和不等式组,找到符合条件的解即可.
【详解】解:设园子的宽为,长为,根据题意得:
,
∴,或,,
∴以下围法均符合题意:
宽为时,长为,
宽为时,长为.
故答案为:长为时,宽为(答案不唯一).
16.30°
【详解】分析:由四边形ABCD为菱形,得到对角线互相垂直,进而得到一对直角相等,再由对顶角相等,得到△AFO与△DFE相似,利用相似三角形对应角相等得到一对角相等,利用ASA得到△AEC与△DOC全等,利用全等三角形对应边相等得到AC=CD,进而确定出△ACD为等边三角形,利用等边三角形的性质及三线合一性质即可求出所求角的度数.
详解:∵菱形ABCD, ∴AC⊥BD,AD=DC, ∵AE⊥CD, ∴∠AEC=∠DOC=90°,
∵∠AOD=∠AED=90°,∠AFO=∠DFE, ∴△AFO∽△DFE, ∴∠CAE=∠CDO,
∴△AEC≌△DOC(ASA), ∴AC=CD, ∴AC=CD=AD,即△ACD为等边三角形,
∵AE⊥CD, ∴AE为∠CAD的平分线, 则∠CAE=30°. 故答案为30°.
点睛:本题主要考查的就是菱形的性质以及三角形全等的判定与性质,综合性较强.解决这个问题的关键就是根据三角形全等的性质得出△ACD为等边三角形.
17./35度
【分析】本题考查了矩形的性质,根据垂直的定义及角的和差求出,根据矩形的性质推出,根据等腰三角形的性质及三角形外角性质求解即可.熟记矩形的性质是解题的关键.
【详解】解:,
,
,
,
四边形是矩形,
,,,
,
,
,
,即,
故答案为:.
18.阴影部分的面积为.
【分析】本题考查了矩形与折叠问题、等腰三角形的判定、勾股定理等知识.先证明,设,从而可得,先在中,利用勾股定理可得的值,再利用三角形的面积公式即可得.
【详解】解:由折叠的性质得:,
∵四边形是长方形,
,
,
,
.
∵四边形是长方形,
,
设,则,
在中,,即,
解得,
即,
则阴影部分的面积为.
19.(1)见解析
(2)见解析
(3)见解析
【分析】本题考查了无刻度直尺作图;矩形的性质,平行四边形的判定和性质,以及全等三角形的判定和性质.
(1)根据网格的特点可得是的中点,作射线,在其上找到一点,使,即可求解;
(2)由图可知,因此将点A向右移动两格即为点G,连接可得;
(3)连接并延长,与的交点即为点H.
【详解】(1)解:如图所示,格点即为所求;
(2)解:如图所示,
理由如下:由图可知,,
四边形以为对角线的平行四边形;
(3)解:如图所示,
理由如下:由(2)知四边形是平行四边形,
,,
,
在和中,
,
,
.
20.(1)6
(2)1;4;9
(3)
【分析】(1)由题意可知,的长度,在时,,求出的长;
(2)当时,,从而得出a和m的值,当时,,从而求得b的值;
(3)分,,三种情况讨论.
【详解】(1)解:当时,的面积不变,
此时:点P在上运动,速度为每秒2个单位,
由题可知,,
当时,的面积为12,
,
,
长方形的长为6.
故答案为:6.
(2)当时,,
,
,
,
,
当时,,
,
,
.
故答案为:1;4;9.
(3)由(1)可知,,
当时,如图,,,
;
当时,如图,,,
;
当时,如图,,,
,
;
故答案为:.
【点睛】本题考查动点问题的函数图象,掌握矩形的性质,三角形的面积公式,利用数形结合的思想解决问题是解题的关键.
21.(1)作图见详解;(2)作图见详解,理由见详解;(3)存在,直线的解析式为,理由见详解
【分析】(1)根据矩形的性质即可求解;
(2)根据正方形的性质即可求解;
(3)根据问题探究的提示,可得直线,运用待定系数法求出直线的解析式,设直线的解析为,用含的式子表示的坐标,根据即可求解的值,由此即可求解.
【详解】解:(1)∵四边形是矩形,
∴,,
∴连接或连接即可将矩形分成面积相等的两部分,如图所示,
;
(2)∵四边形是正方形,
∴如图所示,连接交于点,将正方形平分为四个面积相等的三角形,
∴连接并向两边延长交于点,将线段绕点逆时针旋转,交于点,
∴线段将正方形的面积四等分,
∵四边形是正方形,
∴,,,
∴,
∴,则,
∴,
同理,,,
∵,
∴,且,
∴,则,
同理,,
∴,
即,
∴直线将正方形的面积四等分;
(3)存在直线,理由如下,
如图所示,过点作轴于点,
∵四边形是直角梯形,,
∴,
∴四边形是矩形,
∴连接对角线交于点,连接并向两边延长,交于轴于点,交于点,交于点,
∴点是四边形的对称中心,
当将的面积平分时,则直线平分梯形的面积,
∴直线即为所求,
设直线的解析式为:,且,
∴,则,
∴直线的解析式为:,
∵,且四边形是矩形,
∴矩形是正方形,,
∴,则,
设直线的解析式为,
∴,则,
∴直线的解析式为:,
∵直线交于点,
∴联立方程组得,,
解得,,
∴点,
∵点的横坐标为,且在直线上,
∴,
解得,,即,
∴,
解得,,
∴,
解得,(负值舍去),
∴,
∴直线的解析式为:.
【点睛】本题主要考查矩形,正方形的性质,全等三角形的判定和性质,一次函数等知识的综合,掌握一次函数与几何图形的综合运用是解题的关键.
22.该学生头顶距离感应器2米,感应门会自动打开
【分析】本题考查了矩形的判定,勾股定理,解题的关键是掌握直角三角形两之间边平方和等于斜边平方.
过点D作于点E,通过证明四边形的矩形,得出,,进而得出,根据勾股定理推出,即可解答.
【详解】解:过点D作于点E,
∵,,
∴四边形的矩形,
∴,,
∵,
∴,
根据勾股定理可得:,
∵,
∴感应门会自动打开.
答:该学生头顶距离感应器2米,感应门会自动打开.
23.(1);(2);(3),证明见解析
【分析】本题主要考查了正方形的性质,全等三角形的性质与判定,等腰直角三角形的性质与判定:
(1)①当正方形绕点绕点O转动到其边分别于正方形的两条对角线重合这一特殊位置时,显然;②当正方形绕点绕点O转动到如图位置时,由正方形的性质可得,,,由“”可证,可求解;
(2)连接,仿照仿照(1),,即可可得;
(3)连接EF,由全等三角形的性质可得,则,则由勾股定理可得,则.
【详解】解:(1)①当正方形绕点绕点O转动到其边分别于正方形的两条对角线重合这一特殊位置时,显然,
②当正方形绕点绕点O转动到如图位置时.
四边形是正方形,
,,,
,
,
,
,
四边形的面积正方形的面积,
综上所知,无论正方形绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的.
故答案为:;
(2)连接,
∵,D是斜边的中点,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴两个三角形重叠部分的面积;
故答案为:1;
(3).
证明:
由(1)知,
∴,
∴,
∵四边形是正方形,
∴,
∴
∴.
24.(1)∠CFD=90°;(2)见解析
【分析】(1)由直角三角形的性质及等腰三角形的性质可得出答案;
(2)由(1)可知DF⊥AC,利用等腰△ADC“三合一”的性质证得DE⊥BC,根据有三个角是直角的四边形是矩形,证四边形DECF是矩形.
【详解】解:(1)∵∠ACB=90°,D是AB的中点,
∴AD=CD,
∵DF是∠ADC的角平分线,
∴DF⊥AC.
∴∠CFD=90°;
(2)证明:如图,
∵∠ACB=90°,D是AB的中点,
∴BD=CD,
∵DE是∠BDC的角平分线,
∴DE⊥BC.
∴∠DEC=90°,
∵∠CFD=90°,
∵∠ACB=90°,
∴四边形DECF是矩形.
【点睛】本题主要考查了直角三角形斜边的中线,三线合一定理,矩形的判定,解题的关键在于能够熟练掌握相关知识进行求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一章特殊平行四边形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.分别顺次连接①等腰梯形;②矩形;③菱形;④对角线相等的四边形“各边中点所构成的四边形”中,为菱形的是( )
A.① B.② C.①②③ D.①②④
2.顺次连接对角线相等的四边形各边中点,所得四边形是( ).
A.矩形 B.平行四边形 C.菱形 D.正方形
3.如图,在正方形中,,延长到点,使,连接,动点从点出发以每秒1个单位长度的速度沿向终点运动.设点的运动时间为秒.当和全等时,的值为( )
A.3 B.5 C.7 D.3或7
4.如图,在平面直角坐标系xOy,四边形OABC为正方形,若点B(1,4),则点A的坐标为( )
A.(3,1) B. C. D.(4,1)
5.如图,在正方形ABCD中,点E,F分别在BC,CD边上,△AEF是等边三角形,对角线AC交EF于点G,下列结论:①;②;③AC垂直平分EF;④.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
6.如图,菱形中,.则的度数为( )
A. B. C. D.
7.如图,在矩形中,两条对角线与相交于点,,则的长为( )
A.4 B.8 C. D.
8.下列命题中的真命题是( )
A.有一组邻边相等的四边形是菱形 B.对角线相等的四边形是矩形
C.有一组对边平行的四边形是平行四边形 D.对角线相等的菱形是正方形
9.如图,在矩形中,,垂直平分于点E,则的长为( )
A. B. C.4 D.2
10.在正方形ABCD中,AD=6,点M在边DC上,连接AM,△ADM沿直线AM翻折后点D落到点N,过点N作NE⊥CD,垂足为点E.如图,如果ED=2EC,则DM=( )
A.4+3 B.3+3 C.9﹣3 D.6﹣3
11.如图,E、F、M、N分别是正方形四条边上的点,,则四边形的形状是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
12.已知,如图,平行四边形的两条对角线交于点,设.其中:则满足( )
A. B. C. D.没有数量关系
二、填空题
13.如图,在五边形ABCDE 中,,,,点 A 到直线CD 的距离为
14.已知菱形有一个内角为60°,较短的一条对角线长为8,那么菱形的边长为 .
15.计划利用已有一堵长为米的墙,用篱笆围成面积为12平方米的矩形园子.可用篱笆的总长为11米,可以得到多种围法,如用米长的篱笆作为矩形的宽,用米长的篱笆作为矩形的长等,请你写出其中一种围法,如 .
16.如图,已知菱形ABCD对角线交于点O,AE⊥CD于E,AE=OD,则∠CAE= .
17.如图,矩形的对角线与相交于点,过点作,交于点,连接.若,则 .
三、解答题
18.如图,长方形纸片沿对角线折叠,设点落在处,交于点,,,求阴影部分的面积.
19.图①、图②、图③均是的正方形网格,每个小正方形的边长均为,每个小正方形的顶点叫格点,的顶点和点,均在格点上,点E为边上任一点,只用无刻度的直尺,在给定的网格中,分别按下列要求画图,保留作图痕迹.
(1)在图①中作射线,在其上找到一点,使.
(2)在图②中画以为对角线的平行四边形.
(3)在图③中作射线,在其上找到一点,使.
20.如图1,长方形中,宽为4,点P沿着四边按B→C→D→A方向运动,开始以每秒m个单位匀速运动,a秒后变为每秒2个单位匀速运动,b秒后恢复原速匀速运动,在运动过程中,的面积S与运动时间t的关系如图2所示.
(1)直接写出长方形的长为 ;
(2)直接写出 , , ;
(3)当点P运动到中点时,有一动点Q从点C出发,以每秒1个单位的速度沿C→D→A运动,当一个点到达终点,另一个点也停止运动,设点Q运动的时间为x秒,的面积为y,求当时,y与x之间的关系式.
21.问题探究:
(1)请你在图①中作一条直线,使它将矩形分成面积相等的两部分:
(2)如图②,M是正方形内一定点,请在图②中作出两条直线(要求其中一条直线必须过点M),使它们将正方形的面积四等分,并说明理由.
问题解决:
(3)如图③,在平面直角坐标系中,直角梯形是某市将要筹建的高新技术开发区用地示意图,其中,开发区综合服务管理委员会(其占地面积不计)设在点处.为了方便驻区单位准备过点P修一条笔直的道路(路宽不计),并且使这条路所在的直线l将直角梯形分成面积相等的两部分,你认为直线l是否存在?若存在,求出直线l的表达式;若不存在,请说明理由.
22.如图,某自动感应门的正上方处装着一个感应器,该感应器的有效感应范围不超过,当人体进入感应器的感应范围时,感应门就会自动打开.现已知感应器离地面的高度,一个身高的学生缓慢走到离门的地方时(,假设此时人体与地面垂直),该学生头顶距离感应器多少米?感应门会自动打开吗?
23.探究与证明(八下教材63页《丰富多彩的正方形》)
【课本再现】
(1)如图,正方形的对角线交于点O,点O又是正方形的一个顶点,而且这两个正方形的边长相等,无论正方形绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的 .
【类比迁移】
(2)如图,等腰三角形中,,D是斜边的中点,点D又是直角三角形的直角顶点,,绕点D转动,分别与交于M、N,若,请直接写出两个三角形重叠部分的面积 .
【探索发现】
(3)小刚发现(1)在转动过程中,若边能与边交于点E、F,线段都存在一定的数量关系,请写出数量关系式,并加以证明.
24.如图,在△ABC中,∠ACB=90°,D点是AB的中点,DE、DF分别是△BDC、△ADC的角平分线.
(1)求∠CFD的度数;
(2)求证:四边形FDEC是矩形.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D C D B C B D D B C
题号 11 12
答案 D C
1.D
【分析】根据三角形中位线定理,可得四边形ABCD是平行四边形,再根据菱形的判定,有一组邻边相等的平行四边形是菱形,只要保证四边形的对角线相等即可.
【详解】解:如图,四边形ABCD中,点E,F,G,H分别为AB,BC,CD,AD的中点,连接AC,BD,
∵点E,F,G,H分别为AB,BC,CD,AD的中点,
∴,,
∴,
∴四边形EFGH是平行四边形,
∴连接任意四边形的四边中点都是平行四边形,
当四边形ABCD是等腰梯形时,AC=BD,
∴EH=EF,
此时四边形EFGH是菱形;
当四边形ABCD是矩形时,AC=BD,
∴EH=EF,
此时四边形EFGH是菱形;
当四边形ABCD是菱形时,AC⊥BD,
∴EH⊥EF,
此时四边形EFGH是矩形;
当四边形ABCD的对角线相等时,AC=BD,
∴EH=EF,
此时四边形EFGH是菱形;
∴符合条件的有:①②④.
故选:D
【点睛】本题主要考查了菱形的判定,中点四边形,三角形中位线定理,熟练掌握三角形中位线定理,菱形的判定定理是解题的关键.
2.C
【分析】本题考查菱形的判定和三角形的中位线定理,根据三角形中位线定理得到,再由得到,据此可得四边形是菱形.
【详解】解:如图,E、F、G、H分别是四边形的边的中点,
连接,
根据三角形的中位线定理得,,
∵四边形的对角线相等,
∴,
∴,
∴四边形是菱形.
故选:C.
3.D
【分析】分两种情况,①当点P在BC边上时,②当点P在AD边上时,找出对应的边列式计算即可.
【详解】当点在边上时,在与中,
,
∴.
由题意得,
∴.
当点在上时,在与中,
,
∴,
由题意得,解得.
当点在上时,不满足条件.
∴当的值为3或7时,和全等.
故选D.
【点睛】本题考查的是正方形的性质和全等三角形的性质,能够分情况讨论是解题的关键.
4.B
【分析】过点B作BD⊥y轴于点D,过点A作AE⊥x轴点E,DB与EA的延长线交于点F,通过证明△BFA≌△AEO可得AF=OE,BF=AE;利用B(1,4),可得BD=1,EF=4;通过说明四边形ODFE为矩形,可得DF=OE.计算出线段OE,AE的长即可求得结论.
【详解】解:过点B作BD⊥y轴于点D,过点A作AE⊥x轴点E,DB与EA的延长线交于点F,如图,
∵BD⊥y轴,AE⊥x轴,OD⊥OE,
∴四边形ODFE为矩形,
∴EF=OD,DF=OE,
∵点B(1,4),
∴OD=4,BD=1,
∵四边形OABC为正方形,
∴OA=AB,∠BAO=90°,
∴∠OAE+∠BAF=90°,
∵AE⊥x轴,
∴∠OAE+∠AOE=90°,
∴∠BAF=∠AOE,
在△BAF和△AOE中,
,
∴△BAF≌△AOE(AAS),
∴BF=AE,AF=OE,
∴DF=AF=OE,
∴OE+AE=EF=4,OE﹣AE=BD=1,
∴OE=,AE=,
∴A(,).
故选:B.
【点睛】本题主要考查了正方形的性质,矩形的判定及性质,全等三角形的判定及性质以及坐标与图形,能利用“一线三垂直”构造三角形全等是解题的关键.
5.C
【分析】先根据正方形的性质可得,再根据等边三角形的性质可得,然后根据直角三角形全等的判定定理证出,根据全等三角形的性质即可判断①;先根据全等三角形的性质可得,再根据角的和差即可判断②;先根据角的和差可得,再根据等腰三角形的三线合一即可判断③;先根据等腰直角三角形的判定与性质可得,再利用勾股定理即可判断④.
【详解】解:四边形是正方形,
,
是等边三角形,
,
在和中,,
,
,结论①正确;
,结论②错误;
又,
,即,
垂直平分(等腰三角形的三线合一),结论③正确;
是等腰直角三角形,
,
由勾股定理得:,结论④正确;
综上,正确的结论有3个,
故选:C.
【点睛】本题考查了正方形的性质、等边三角形的性质、勾股定理、直角三角形全等的判定定理与性质等知识点,熟练掌握各判定定理与性质是解题关键.
6.B
【分析】证明,平分,可得,,求解,,从而可得答案.
【详解】解:∵菱形,
∴,平分,
∴,,
∵,
∴,,
∴,
∴,
故选B
【点睛】本题考查的是菱形的性质,平行线的性质,角平分线的定义,熟记的菱形的性质是解本题的关键.
7.D
【分析】利用矩形的性质可知对角线互相平分且,再利用勾股定理求解即可.
【详解】解:在矩形中,
故选D.
【点睛】本题主要考查矩形的性质及勾股定理,熟练掌握矩形的性质及勾股定理求直角边是解决本题的关键.
8.D
【分析】根据菱形、矩形、平行四边形、正方形的判定逐项判断即可.
【详解】解:A、是假命题,因为:有一组邻边相等的平行四边形是菱形;
B、是假命题,例如等腰梯形;
C、是假命题,例如梯形;
D、是真命题,符合正方形的判定定理,
故选:D.
【点睛】本题考查了判断命题真假,熟练掌握菱形、矩形、平行四边形、正方形的判定定理是解题的关键.
9.B
【分析】由矩形的性质和线段垂直平分线的性质可证是等边三角形,可得,即可求解.
【详解】解:∵四边形是矩形,
∴,,
∵垂直平分,
∴,
∴,
∴是等边三角形,
∴,
∴,
∴.
故选:B.
【点睛】本题考查了矩形的性质,线段垂直平分线的性质,等边三角形的判定和性质,直角三角形的性质,灵活运用这些性质解决问题是解题的关键.
10.C
【分析】过点N作NH⊥AD于H,先证明四边形NEDH为矩形,得到HD=NE,NH=DE,根据ED=2EC,ED+EC=CD=6,可以得到ED=HN=4,再利用勾股定理求出AH,即可得到NE的值,最后再直角三角形MNE中用勾股定理求解即可.
【详解】解:如图所示,过点N作NH⊥AD于H,
∵四边形ABCD是正方形,AD=6
∴AD=CD=6,∠D=90°,
∵NE⊥CD,NH⊥AD,
∴∠NED=∠NHD=∠NHA=90°,
∴四边形NEDH为矩形,
∴HD=NE,NH=DE,
∵ED=2EC,ED+EC=CD=6,
∴ED=HN=4,
由翻折的性质可得AD=AN=6,DM=MN
∴,
∴,
设DM=MN=x,则ME=4-x,
则,
∴,
解得,
∴,
故选C.
【点睛】本题主要考查了矩形的性质与判定,正方形的性质,折叠的性质,勾股定理,解题的关键在于能够熟练掌握相关知识进行求解.
11.D
【分析】根据正方形的四边相等,四个角都是,,得到,推出,,,全等,得到,,,推出四边形是菱形,根据,推出.得到,从而得出四边形是正方形.
【详解】解:四边形是正方形.
证明:∵四边形是正方形,
∴
∵,
∴.
∵,
∴.
∴,
∴四边形是菱形.
∵,,
∴.
∴.
∴四边形是正方形.
故选:D.
【点睛】本题主要考查了正方形,全等三角形等,熟练掌握正方形的判定和性质,全等三角形的判定和性质,是解题的关键.
12.C
【分析】根据平行四边形的性质,得到AO=,BO=,然后在△ABO中,利用三角形两边之和大于第三边,两边之差小于第三边得到.
【详解】∵四边形ABCD是平行四边形,AC=z,BD=y
∴AO=,BO=
在△ABO中,两边之和大于第三边,两边之差小于第三边,即:
故选:C
【点睛】本题考查平行四边形的性质和三角形三边的关系,解题关键是利用平行四边形的性质,将x、y、z转化到同一个三角形中去.
13.
【分析】延长ED与BC交于点F,作AH⊥DC于点H,先证明出四边形AEFB是正方形,然后将△ABC逆时针旋转90°得到△AEG,通过证明△GAD≌△CAD证明出AH=AE最终得出答案.
【详解】
如图,延长ED与BC交于点F,作AH⊥DC于点H,
∵,
∴四边形AEFB是矩形,
∵AB=AE,
∴四边形AEFB是正方形,
将△ABC逆时针旋转90°得到△AEG,如图所示,
则AG=AC,∠GAE=∠CAB,
∵,
∴∠CAB+∠DAE=45°,
∴∠GAD=∠GAE+∠DAE=45°,
∴∠GAD=∠CAD,
在△GAD与△CAD中,
∵GA=CA,∠GAD=∠CAD,AD=AD,
∴△GAD≌△CAD(SAS),
∴AH=AE=,
故答案为.
【点睛】本题主要考查了正方形与全等三角形的综合运用,熟练掌握相关概念是解题关键.
14.8
【分析】先画出图形,根据菱形的性质,可证得△ABC为等边三角形,据此即可解答.
【详解】解:由题意得,∠ABC=60°,AC=8,
∵四边形ABCD是菱形,
∴BA=BC,
∴△ABC是等边三角形,
∴AB=AC=8,
故答案为:8.
【点睛】本题考查了菱形的性质,等边三角形的判定与性质,解答本题的关键是熟练掌握菱形的性质.
15.长为时,宽为(答案不唯一)
【分析】本题考查了方程与不等式的应用,设园子的宽为,长为,根据题意列出方程和不等式组,找到符合条件的解即可.
【详解】解:设园子的宽为,长为,根据题意得:
,
∴,或,,
∴以下围法均符合题意:
宽为时,长为,
宽为时,长为.
故答案为:长为时,宽为(答案不唯一).
16.30°
【详解】分析:由四边形ABCD为菱形,得到对角线互相垂直,进而得到一对直角相等,再由对顶角相等,得到△AFO与△DFE相似,利用相似三角形对应角相等得到一对角相等,利用ASA得到△AEC与△DOC全等,利用全等三角形对应边相等得到AC=CD,进而确定出△ACD为等边三角形,利用等边三角形的性质及三线合一性质即可求出所求角的度数.
详解:∵菱形ABCD, ∴AC⊥BD,AD=DC, ∵AE⊥CD, ∴∠AEC=∠DOC=90°,
∵∠AOD=∠AED=90°,∠AFO=∠DFE, ∴△AFO∽△DFE, ∴∠CAE=∠CDO,
∴△AEC≌△DOC(ASA), ∴AC=CD, ∴AC=CD=AD,即△ACD为等边三角形,
∵AE⊥CD, ∴AE为∠CAD的平分线, 则∠CAE=30°. 故答案为30°.
点睛:本题主要考查的就是菱形的性质以及三角形全等的判定与性质,综合性较强.解决这个问题的关键就是根据三角形全等的性质得出△ACD为等边三角形.
17./35度
【分析】本题考查了矩形的性质,根据垂直的定义及角的和差求出,根据矩形的性质推出,根据等腰三角形的性质及三角形外角性质求解即可.熟记矩形的性质是解题的关键.
【详解】解:,
,
,
,
四边形是矩形,
,,,
,
,
,
,即,
故答案为:.
18.阴影部分的面积为.
【分析】本题考查了矩形与折叠问题、等腰三角形的判定、勾股定理等知识.先证明,设,从而可得,先在中,利用勾股定理可得的值,再利用三角形的面积公式即可得.
【详解】解:由折叠的性质得:,
∵四边形是长方形,
,
,
,
.
∵四边形是长方形,
,
设,则,
在中,,即,
解得,
即,
则阴影部分的面积为.
19.(1)见解析
(2)见解析
(3)见解析
【分析】本题考查了无刻度直尺作图;矩形的性质,平行四边形的判定和性质,以及全等三角形的判定和性质.
(1)根据网格的特点可得是的中点,作射线,在其上找到一点,使,即可求解;
(2)由图可知,因此将点A向右移动两格即为点G,连接可得;
(3)连接并延长,与的交点即为点H.
【详解】(1)解:如图所示,格点即为所求;
(2)解:如图所示,
理由如下:由图可知,,
四边形以为对角线的平行四边形;
(3)解:如图所示,
理由如下:由(2)知四边形是平行四边形,
,,
,
在和中,
,
,
.
20.(1)6
(2)1;4;9
(3)
【分析】(1)由题意可知,的长度,在时,,求出的长;
(2)当时,,从而得出a和m的值,当时,,从而求得b的值;
(3)分,,三种情况讨论.
【详解】(1)解:当时,的面积不变,
此时:点P在上运动,速度为每秒2个单位,
由题可知,,
当时,的面积为12,
,
,
长方形的长为6.
故答案为:6.
(2)当时,,
,
,
,
,
当时,,
,
,
.
故答案为:1;4;9.
(3)由(1)可知,,
当时,如图,,,
;
当时,如图,,,
;
当时,如图,,,
,
;
故答案为:.
【点睛】本题考查动点问题的函数图象,掌握矩形的性质,三角形的面积公式,利用数形结合的思想解决问题是解题的关键.
21.(1)作图见详解;(2)作图见详解,理由见详解;(3)存在,直线的解析式为,理由见详解
【分析】(1)根据矩形的性质即可求解;
(2)根据正方形的性质即可求解;
(3)根据问题探究的提示,可得直线,运用待定系数法求出直线的解析式,设直线的解析为,用含的式子表示的坐标,根据即可求解的值,由此即可求解.
【详解】解:(1)∵四边形是矩形,
∴,,
∴连接或连接即可将矩形分成面积相等的两部分,如图所示,
;
(2)∵四边形是正方形,
∴如图所示,连接交于点,将正方形平分为四个面积相等的三角形,
∴连接并向两边延长交于点,将线段绕点逆时针旋转,交于点,
∴线段将正方形的面积四等分,
∵四边形是正方形,
∴,,,
∴,
∴,则,
∴,
同理,,,
∵,
∴,且,
∴,则,
同理,,
∴,
即,
∴直线将正方形的面积四等分;
(3)存在直线,理由如下,
如图所示,过点作轴于点,
∵四边形是直角梯形,,
∴,
∴四边形是矩形,
∴连接对角线交于点,连接并向两边延长,交于轴于点,交于点,交于点,
∴点是四边形的对称中心,
当将的面积平分时,则直线平分梯形的面积,
∴直线即为所求,
设直线的解析式为:,且,
∴,则,
∴直线的解析式为:,
∵,且四边形是矩形,
∴矩形是正方形,,
∴,则,
设直线的解析式为,
∴,则,
∴直线的解析式为:,
∵直线交于点,
∴联立方程组得,,
解得,,
∴点,
∵点的横坐标为,且在直线上,
∴,
解得,,即,
∴,
解得,,
∴,
解得,(负值舍去),
∴,
∴直线的解析式为:.
【点睛】本题主要考查矩形,正方形的性质,全等三角形的判定和性质,一次函数等知识的综合,掌握一次函数与几何图形的综合运用是解题的关键.
22.该学生头顶距离感应器2米,感应门会自动打开
【分析】本题考查了矩形的判定,勾股定理,解题的关键是掌握直角三角形两之间边平方和等于斜边平方.
过点D作于点E,通过证明四边形的矩形,得出,,进而得出,根据勾股定理推出,即可解答.
【详解】解:过点D作于点E,
∵,,
∴四边形的矩形,
∴,,
∵,
∴,
根据勾股定理可得:,
∵,
∴感应门会自动打开.
答:该学生头顶距离感应器2米,感应门会自动打开.
23.(1);(2);(3),证明见解析
【分析】本题主要考查了正方形的性质,全等三角形的性质与判定,等腰直角三角形的性质与判定:
(1)①当正方形绕点绕点O转动到其边分别于正方形的两条对角线重合这一特殊位置时,显然;②当正方形绕点绕点O转动到如图位置时,由正方形的性质可得,,,由“”可证,可求解;
(2)连接,仿照仿照(1),,即可可得;
(3)连接EF,由全等三角形的性质可得,则,则由勾股定理可得,则.
【详解】解:(1)①当正方形绕点绕点O转动到其边分别于正方形的两条对角线重合这一特殊位置时,显然,
②当正方形绕点绕点O转动到如图位置时.
四边形是正方形,
,,,
,
,
,
,
四边形的面积正方形的面积,
综上所知,无论正方形绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的.
故答案为:;
(2)连接,
∵,D是斜边的中点,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴两个三角形重叠部分的面积;
故答案为:1;
(3).
证明:
由(1)知,
∴,
∴,
∵四边形是正方形,
∴,
∴
∴.
24.(1)∠CFD=90°;(2)见解析
【分析】(1)由直角三角形的性质及等腰三角形的性质可得出答案;
(2)由(1)可知DF⊥AC,利用等腰△ADC“三合一”的性质证得DE⊥BC,根据有三个角是直角的四边形是矩形,证四边形DECF是矩形.
【详解】解:(1)∵∠ACB=90°,D是AB的中点,
∴AD=CD,
∵DF是∠ADC的角平分线,
∴DF⊥AC.
∴∠CFD=90°;
(2)证明:如图,
∵∠ACB=90°,D是AB的中点,
∴BD=CD,
∵DE是∠BDC的角平分线,
∴DE⊥BC.
∴∠DEC=90°,
∵∠CFD=90°,
∵∠ACB=90°,
∴四边形DECF是矩形.
【点睛】本题主要考查了直角三角形斜边的中线,三线合一定理,矩形的判定,解题的关键在于能够熟练掌握相关知识进行求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
