3.1用树状图或表格求概率同步练习(含解析)
文档属性
| 名称 | 3.1用树状图或表格求概率同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-15 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
3.1用树状图或表格求概率
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.甲、乙两人参加社会实践活动,随机选择“打扫社区卫生”和“参加社会调查”其中一项,那么两人同时选择“参加社会调查”的概率为( )
A. B. C. D.
2.有4张扑克牌如图所示,将其背面朝上,打乱顺序后放在桌面上.若从中随机抽取两张,则抽到的花色均为 (黑桃)的概率为( )
A. B. C. D.
3.一个不透明的袋中有四张完全相同的卡片,把它们分别标上数字1、2、3、4.随机抽取两张卡片,则两次抽取的卡片上数字之积为偶数的概率是( )
A. B. C. D.
4.为了疫情防控,某小区需要从甲、乙、丙、丁 4名志愿者中随机抽取2名负责该小区入口处的测温工作,则甲被抽中的概率是( )
A. B. C. D.
5.信阳是河南传统餐饮历史文化名城,信阳菜历经千年的积淀和发展,以鲜、香、爽、醇、中的独特味道传遍大江南北.某游客慕名而来,决定从“筒鲜鱼”“固始鹅块”“石凉粉”“罗山大肠汤”“闷罐肉”这5个特色美食中随机选取2 个进行品尝,则他抽到“筒鲜鱼”和“固始鹅块”的概率为( )
A. B. C. D.
6.一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3,随机摸出一个小球然后放回,再随机摸出一个小球,则两次摸出小球的标号相同的概率是( )
A. B. C. D.
7.某班甲、乙、丙、丁四个人站一横排照毕业相,则甲、乙两人恰好相邻的概率是( )
A. B. C. D.
8.在一个不透明的袋中装有2个黄球和2个红球,它们除颜色外没有其他区别,从袋中任意摸出一个球,然后放加搅匀,再从袋中任意摸一个球,那么两次都摸到黄球的概率是( )
A. B. C. D.
9.经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,那么两辆汽车经过这个十字路口时,第一辆车向左转,第二辆车向右转的概率是( ).
A. B. C. D.
10.在一个不透明的袋子中有3个白球、4个红球,这些球除颜色不同外其他完全相同.从袋子中随机摸出一个球,它是红球的概率是( )
A. B. C. D.
11.在“少年强则国强”这句话中,“强”字出现的频率是( )
A. B. C. D.
12.河南省有五处世界文化遗产:1.龙门石窟;2安阳殷墟;3.登封天地之中历史建筑群;4.大运河河南段;5.丝绸之路河南段.小明和小亮从中分别随机选取一个在五一期间参观,则正好选龙门石窟和安阳殷墟的概率为( )
A. B. C. D.
二、填空题
13.如图,开关,和处于断开状态,随机闭合开关,和中的两个,两盏灯同时发光的概率为 .
14.从一副54张牌的扑克牌中任取一张,它是梅花的概率是 .
15.邮票素有“国家名片”之称,方寸之间,包罗万象,为宣传北京2022年冬奥会,中国邮政发行了若干套冬奥会纪念邮票,其中有一套展现雪上运动的邮票,如图所示,某班级举行冬奥会有奖问答活动,在抢答环节中,若答对两题,可从4枚邮票中任意抽取2枚作为奖品,则恰好抽到“高山滑雪”和“自由式滑雪”的概率为 .
16.把一转盘先分成两个半圆,再把其中一个半圆等分成三等份,并标上数字如图所示,任意转动转盘,当转盘停止时,指针落在奇数区域的概率是 .
17.在一个不透明的袋子中有个除颜色外完全相同的小球,其中绿球个,红球个,摸出一个球不放回,混合均匀后再摸出一个球,两次都摸到红球的概率是 .
三、解答题
18.已知代数式.
(1)化简代数式;
(2)在满足的整数中随机抽取1个代入代数式中,求不会使得代数式无意义的概率.
19.根据教育部发布的《义务教育劳动课程标准(2022年版)》要求,2022年秋季开学起,劳动课将成为中小学生的一门独立课程.学期初清溪中学为了解本校学生对劳动课的重视程度,随机在校内调查了部分学生,调查结果分为“非常重视”“重视”“比较重视”“不重视”四类,并将结果绘制成如图所示的两幅不完整的统计图.根据图中信息,解答下列问题:
(1)在扇形统计图中,“非常重视”所占的圆心角的度数为__________,请补全条形统计图;
(2)对劳动课“非常重视”的4人中有一名男生,三名女生,若从中随机抽取两人作为“劳动教育宣传大使”,请利用画树状图法或列表法,求出恰好抽到的都是女生的概率.
20.某校为庆祝“五四青年节”,在2018年4月底组织该校学生举办了“传承五四精神共建和谐社土会”的演讲比赛.为了解学生在演讲比赛中的成绩情况,学校随机抽取了部分学生的演讲比赛成绩进行统计(满分:100分,等次:A.优秀:90~100分;B.良好:80﹣89分;C.一般:60﹣79分;D.较差:60分以下,不含60分)得到如下不完整的图表:
等次 频数 频率
A a 0.25
B b 0.5
C 3 m
D 2 0.1
根据以上信息解答下列问题
(1)表中a=_____,b=_____,m=_______,并补全频数分布直方图;
(2)根据抽查学生演讲成绩频数统计表制作的扇形统计图中,表示C等次部分的扇形中心角的度数是_______;
(3)若A等次中有2名女生,其余为男生,学校准备从A等次学生中抽取2名学生组成演讲组合参加全市“五四青年杯”演讲比赛,求恰好抽取1名男生和1名女生的概率.
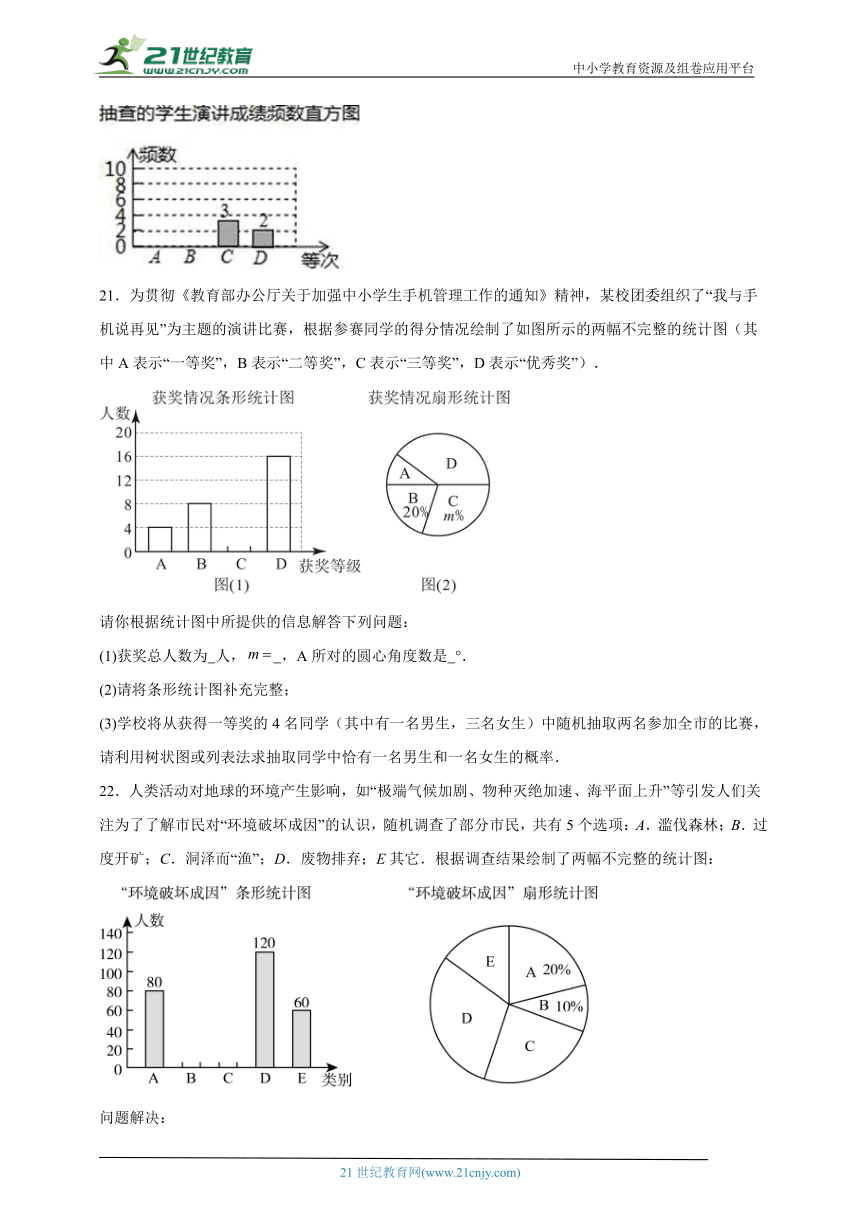
21.为贯彻《教育部办公厅关于加强中小学生手机管理工作的通知》精神,某校团委组织了“我与手机说再见”为主题的演讲比赛,根据参赛同学的得分情况绘制了如图所示的两幅不完整的统计图(其中A表示“一等奖”,B表示“二等奖”,C表示“三等奖”,D表示“优秀奖”).
请你根据统计图中所提供的信息解答下列问题:
(1)获奖总人数为 人, ,A所对的圆心角度数是 °.
(2)请将条形统计图补充完整;
(3)学校将从获得一等奖的4名同学(其中有一名男生,三名女生)中随机抽取两名参加全市的比赛,请利用树状图或列表法求抽取同学中恰有一名男生和一名女生的概率.
22.人类活动对地球的环境产生影响,如“极端气候加剧、物种灭绝加速、海平面上升”等引发人们关注为了了解市民对“环境破坏成因”的认识,随机调查了部分市民,共有5个选项:A.滥伐森林;B.过度开矿;C.洞泽而“渔”;D.废物排弃;E其它.根据调查结果绘制了两幅不完整的统计图:
问题解决:
(1)本次调查活动中,调查的人数有______人,采取的调查方式是______(填上“普查”或“抽样调查”);
(2)在扇形统计图中,求“C”组所在扇形的圆心角的度数;
(3)若该市人口约有100万人,则可以估计其中持“D”组观点的市民人数约有______人:
(4)“保护生存环境建设美好家园”是实验学校开展环保类社团活动之宗旨,学校利用假期开设了四个如图所示的环保类社团项目,每人只能从这四个项目中随机选择一个项目,每一个项目被选择的可能性相同.小华和小聪分别从这四个项目中选择一个,请用列表或画树状图的方法,求小华和小聪选择同一个项目的概率.
社团名称 A(环保义工) B(绿植养护) C(回收材料) D(垃圾分类)
23.已知关于x的一元二次方程x2+bx+c=0.
(1)c=2b﹣1时,求证:方程一定有两个实数根.
(2)有甲、乙两个不透明的布袋,甲袋中装有3个除数字外完全相同的小球,分别标有数字1,2,3,乙袋中装有4个除数字外完全相同的小球,分别标有数字1,2,3,4,从甲袋中随机抽取一个小球,记录标有的数字为b,从乙袋中随机抽取一个小球,记录标有的数字为c,利用列表法或者树状图,求b、c的值使方程x2+bx+c=0有两个相等的实数根的概率.
24.新角度·概率、几何结合 如图(1),线段和相交于点C,连接.四张纸牌除正面分别写着如图(2)所示的四个不同的条件外完全相同,将四张纸牌背面朝上洗匀后放在桌面上.
(1)若小明第一次抽到纸牌③后,再从剩下的三张纸牌中随机抽取一张,则两张纸牌上的条件能证明成立的概率是_________;
(2)若从四张纸牌中随机抽出两张,求两张纸牌上的条件能证明成立的概率,先补全图(3)中的树状图,再计算.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B B D A C A A C B D
题号 11 12
答案 B B
1.B
【详解】试题解析:可能出现的结果
小明 打扫社区卫生 打扫社区卫生 参加社会调查 参加社会调查
小华 打扫社区卫生 参加社会调查 参加社会调查 打扫社区卫生
由上表可知,可能的结果共有种,且都是等可能的,其中两人同时选择“参加社会调查”的结果有种,
则所求概率
故选B.
点睛:求概率可以用列表法或者画树状图的方法.
2.B
【分析】本题主要考查了简单的概率计算,正确求出黑桃花色的概率是解题的关键.根据树状图列出所有的可能的结果,即可得到花色均为黑桃的概率.
【详解】解:设4张扑克牌为A,B,C,D,画树状图如图所示,
所有等可能情况数为12种,其中两张花色均为 (黑桃)的扑克牌有2种,
则抽到的花色均为 (黑桃)的概率为.
故选:B.
3.D
【分析】列举展示所有6种等可能的结果数,再找出两次抽取的卡片上数字之积为偶数的结果数,然后根据概率公式求解.
【详解】解:两次抽取的卡片上数字为:(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)
共有6种等可能的结果数,其中两次抽取的卡片上数字之积为偶数的结果数为5,
所以两次抽取的卡片上数字之积为偶数的概率=
故选D.
【点睛】本题考查了列表法与树状图法,解题关键在于利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.
4.A
【分析】根据题意画出树状图,然后求得全部情况的总数与符合条件的情况数目;二者的比值就是其发生的概率.
【详解】解:画树状图得:
∴一共有12种情况,抽取到甲的有6种,
∴P(抽到甲)= .
故选:A.
【点睛】本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,用到的知识点为:概率=所求情况数与总情况数之比.
5.C
【分析】通过列表法列出所有情况,再根据抽到“筒鲜鱼”和“固始鹅块”的情况数利用概率公式进行计算即可.
【详解】记“筒鲜鱼”“固始鹅块”“石凉粉”“罗山大肠汤”“闷罐肉”分别为A、B、C、D、E.抽到“筒鲜鱼”和“固始鹅块”即为AB或BA,则5个特色美食中随机选取2个进行品尝的所有可能情况列表为:
A B C D E
A AB AC AD AE
B AB BC BD BE
C AC BC CD CE
D AD BD CD DE
E AE BE CE DE
共有20种等可能事件,其中抽到AB或BA的有2种,
到AB或BA的概率为
即抽到“筒鲜鱼”和“固始鹅块”的概率为.
故选:C.
【点睛】本题考查了列表法或画树状图法求概率,即一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包括其中的m种结果,那么事件A发生的概率.
6.A
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的小球的标号相同的情况,再利用概率公式即可求得答案.
【详解】解:根据题意,画树状图如下:
共有9种等可能结果,其中两次摸出的小球的标号相同的有3种,
∴两次摸出的小球的标号相同的概率是,
故选:A.
【点睛】此题考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
7.A
【分析】根据列举法可进行求解概率.
【详解】解:由题意可知甲、乙、丙、丁排成一排的情况有:甲乙丙丁,甲乙丁丙,甲丙乙丁,甲丙丁乙,甲丁乙丙,甲丁丙乙,乙甲丙丁,乙甲丁丙,乙丙甲丁,乙丙丁甲,乙丁甲丙,乙丁丙甲,丙甲乙丁,丙甲丁乙,丙乙甲丁,丙乙丁甲,丙丁甲乙,丙丁乙甲,丁甲乙丙,丁甲丙乙,丁乙甲丙,丁乙丙甲,丁丙甲乙,丁丙乙甲,共24种,其中甲乙两人恰好相邻的有12种,所以甲、乙两人恰好相邻的概率是;
故选A.
【点睛】本题主要考查概率,熟练掌握概率的求解是解题的关键.
8.C
【分析】用树状图或列表法,列出所有等可能的情况数量n,找出符合题意的情况数量m,则概率为P= .
【详解】解:如下表:
第一次 第二次 黄球 黄球 红球 红球
黄球 (黄球,黄球) (黄球,黄球) (红球,黄球) (红球,黄球)
黄球 (黄球,黄球) (黄球,黄球) (红球,黄球) (红球,黄球)
红球 (黄球,红球) (黄球,红球) (红球,红球) (红球,红球)
红球 (黄球,红球) (黄球,红球) (红球,红球) (红球,红球)
一共有16种等可能的情况,
(黄球,黄球)的一共有4种,则两次都摸到黄球的概率P= ;
故选:C.
【点睛】考查列表法解决概率问题;找到两次都摸到黄球的情况数是解决本题的关键;用到的知识点为:概率等于所求情况数与总情况数之比.
9.B
【分析】根据题意可画出树状图,得到等可能的情况有9种,其中第一辆向左转,第二辆向右转的情况有1种,最后根据概率公式计算可得.
【详解】根据题意画出树状图如图所示,
由图可知这两辆汽车行驶方向共有9种等可能的情况,其中第一辆向左转,第二辆向右转的情况有1种,
∴第一辆向左转,第二辆向右转的概率为.
故选B.
【点睛】本题主要考查树状图法或列表法求概率.解题的关键是根据题意画出树状图或列出表格.
10.D
【分析】根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率,即可求出答案.
【详解】解:根据题意可得:袋子中有有3个白球,4个红球,共7个,
从袋子中随机摸出一个球,它是红色球的概率是;
故选:D.
【点睛】此题考查了概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.
11.B
【分析】这句话中总共6字,“强”出现了2次,则答案可求.
【详解】∵“少年强则国强”这句话共6个字,“强”出现了2次,
∴“强”字出现的频率是
故选:B.
【点睛】本题主要考查随机事件的概率,掌握概率公式是解题的关键.
12.B
【分析】本题主要考查了用树状图或列表法求概率,列出表格得出等可能情况,再找选中龙门石窟和安阳殷墟的情况,最后根据概率公式求解即可.
【详解】解:按照1.龙门石窟;2安阳殷墟;3.登封天地之中历史建筑群;4.大运河河南段;5.丝绸之路河南段.列表如下:
1 2 3 4 5
1 (1,1) (1,2) (1,3) (1,4) (1,5)
2 (2,1) (2,2) (2,3) (2,4) (2,5)
3 (3,1) (3,2) (3,3) (3,4) (3,5)
4 (4,1) (4,2) (4,3) (4,4) (4,5)
5 (5,1) (5,2) (5,3) (5,4) (5,5)
从列出中看,一共由25中等可能情况,选中1龙门石窟和2安阳殷墟的情况有2种,
故正好选龙门石窟和安阳殷墟的概率为:.
故选:B.
13.
【分析】本题主要考查了用树状图或列表法求等可能事件的概率,方法是用树状图或列表法列举出所有可能出现的结果总数,找出符合条件的结果数,用分数表示即可,注意每种情况发生的可能性相等.利用画树状图或列表的方法,得出所有可能出现的结果总数,从中找到符合条件的结果数,进而求出概率即可.
【详解】解:画树状图,如图所示:
∵共有6种等可能的结果,能让两盏灯泡同时发光的有2种情况,
∴能让两盏灯泡同时发光的概率为:.
14..
【分析】根据概率公式直接计算即可得到答案.
【详解】根据题意,一副54张牌的扑克牌中,是梅花的有13张梅花,
故从中任取一张牌刚好是梅花的概率是,
故答案为:.
【点睛】本题主要考查概率公式,掌握随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数是解题的关键.
15.
【分析】画树状图,共有12种等可能结果,其中恰好抽到“高山滑雪”和“自由式滑雪”的有2种结果,再由概率公式求解即可.
【详解】“越野滑雪”、“高山滑雪”、“冬季两项”、“自由式滑雪”分别记为甲、乙、丙、丁,
画树状图如下:
共有12种等可能结果,其中恰好抽到乙和丁即“高山滑雪”和“自由式滑雪”的有2种结果,
∴恰好抽到“高山滑雪”和“自由式滑雪”的概率为:.
【点睛】此题考查的是用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
16.
【分析】根据几何概率的求法:指针落在奇数区域的概率是就是所标数字为奇数的面积与总面积的比值.
【详解】解:观察这个图可知:所标数字为奇数的面积占总面积的,
∴指针落在奇数区域的概率是.
故答案为:.
【点睛】本题考查了几何概率的计算,理解并掌握“概率=相应的面积与总面积之比”是解题关键.
17.
【分析】运用画树状图的方法把所有等可能结果都表示出来,再运用概率的计算方法即可求解.
【详解】解:画树状图把所有等可能结果表示出来,
共有种等可能结果,其中两次摸到红球的结果有种,
∴两次都摸到红球的概率是,
故答案为:.
【点睛】本题主要列表法或画树状图法求随机事件的概率,掌握以上知识,数形结合分析是解题的关键.
18.(1)
(2)
【分析】(1)根据分式的混合运算法则计算即可解答;
(2)先求出满足的整数,再求出分式有意义的条件即可解答.
【详解】(1)解:
;
(2)解:在区间上的整数有,,0,1,2,共个,
由(1)得,分式有意义的条件为:且,即可取0,1,
∴不会使得代数式无意义的概率为.
【点睛】本题考查了分式的运算法则,分式有意义的条件及列举法求概率,解题的关键是熟练掌握以上知识点并保持计算准确.
19.(1)18°,见解析
(2)
【分析】(1)由“不重视”的人数和所占百分比可以求出抽查的总人数,再根据“比较重视”的人数即可得到其对应圆心角度数,用总人数减去已知三类的人数可以得到“重视”的人数,据此可以补全条形统计图;
(2)把三名女生分别记为,,,根据题意画出树状图即可得到解答.
【详解】(1)解: 调查的总人数为,
对劳动课“重视”的人数为,
,
补全条形统计图如下:
(2)解:画出树状图如下:
共有12种等可能的结果,其中抽到的都是女生的结果有6种,
所以恰好抽到的都是女生的概率为.
【点睛】本题考查数据的整理和分析,熟练掌握扇形统计图圆心角的求法、由样本所占百分比估计总体数量的方法、用列表法或树状图法求概率的方法是解题关键关键.
20.(1)5、10、0.15;(2)54°;(3).
【分析】(1)由D等次人数及其频率求得总人数,再根据“频率=频数÷总数”求解可得答案;
(2)用360°乘以C等次的频率即可得;
(3)列树形图后即可将所有情况全部列举出来,从而求得恰好抽中这两人的概率.
【详解】(1)∵被调查的总人数为2÷0.1=20,
∴a=20×0.25=5、b=20×0.5=10、m=3÷20=0.15,
补全图形如下:
故答案为5、10、0.15;
(2)表示C等次部分的扇形中心角的度数是360°×0.15=54°,
故答案为54°;
(3)画出树状图如下:
共有20种情况,其中“恰好是1名男生和1名女生”的情况有12种,
所以恰好是1名男生和1名女生的概率为=.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
21.(1)40,30,36
(2)见解析
(3)
【分析】(1)等级的人数除以所占的百分比,求出总人数,等级的人数除以总人数求出的值,等级所占的比例,求出圆心角;
(2)根据(1)中求出的等级的人数求出总人数;
(3)画出树状图进行求解即可.
【详解】(1)解:(人),等级的人数为:(人),
∴,
∴,
A所对的圆心角度数是;
故答案为:40,30,36;
(2)补全条形图如下:
(3)画出树状图如下:
共有12种等可能的结果,其中选择一男一女,共有6种等可能的结果,
∴.
【点睛】本题考查条形图和扇形图的综合应用,树状图法求概率.从统计图中有效的获取信息,是解题的关键.
22.(1)400,抽样调查
(2)
(3)30万
(4)
【分析】本题主要考查了扇形统计图与条形统计图信息相关联,树状图法或列表法求解概率,用样本估计总体:
(1)用A类别的人数除以其人数占比可以求出参与调查的人数,根据题意可知采用的是抽样调查方式;
(2)先求出B类别的人数,进而求出C类别的人数,再用360度乘以C类别的人数占比即可得到答案;
(3)用100万乘以样本中D类别的人数占比即可得到答案;
(4)先列表得到所有等可能性的结果数,再找到小华和小聪选择同一个项目的结果数,最后依据概率计算公式求解即可.
【详解】(1)解:人,
∴本次调查活动中,调查的人数有400人,
由题意得,采取的调查方式是抽样调查,
故答案为:400,抽样调查;
(2)解:B类别的人数为人,
∴C类别的人数为人,
∴在扇形统计图中,“”组所在扇形的圆心角等于;
(3)解:万人,
∴估计其中持“”组观点的市民人数约有30万人,
故答案为:30万;
(4)列表如下:
D
D
由表格可知共有16中等可能性的结果数,其中小华和小聪选择同一个项目的结果数有4种,
∴小华和小聪选择同一个项目的概率为.
23.(1)证明见解析;(2).
【分析】(1)把c=2b﹣1代入x2+bx+c=0.利用一元二次方程根的判别式即可得答案;
(2)根据方程x2+bx+c=0有两个相等的实数根,利用判别式可得b与c的关系,画出树状图,得出所有可能情况数及符合b与c的关系的情况数,利用概率公式即可得答案.
【详解】(1)∵c=2b﹣1,
∴x2+bx+c=x2+bx+2b=0.
∵==≥0,
∴方程一定有两个实数根.
(2)∵方程x2+bx+c=0有两个相等的实数根,
∴=0,
∴,
画树状图如下:
由树状图可知:所有可能情况数为12种,符合的情况数为2种,
∴b、c的值使方程x2+bx+c=0有两个相等的实数根的概率为=.
【点睛】本题考下一元二次方程的根的判别式及树状图法或列表法求概率,对于一元二次方程(),根的判别式为△=,当△>0时,方程有两个不相等的实数根,当△=0时,方程有两个相等的实数根,当△<0时,方程没有实数根;熟练掌握根的判别式及概率公式是解题关键.
24.(1)
(2)摸出两张纸牌上的条件能证明成立的概率.
【分析】(1)根据全等三角形的判定得到能证明成立的结果数,利用概率公式即可求解;
(2)补全树状图,共有12个可能的结果,根据全等三角形的判定得到能证明成立的结果数,即可得求出概率.
【详解】(1)解:∵,,
∴当抽中时,由能判断,①符合题意;
当抽中时,由能判断,②符合题意;
当抽中时,由不能判断,④不符合题意;
∴共有三种等可能结果,其中能证明成立的情况有2种
能证明概率是,
故答案为:;
(2)解:补全树状图,如图,
∵,
∴当抽中①,②,不能判断;
当抽中①,③,能判断;
当抽中①,④,能判断;
当抽中②,①,不能判断;
当抽中②,③,能判断;
当抽中②,④,能判断;
当抽中③,①,能判断;
当抽中③,②,能判断;
当抽中③,④,不能判断;
当抽中④,①,能判断;
当抽中④,②,能判断;
当抽中④,③,不能判断;
共有12个可能的结果,两张纸牌上的条件能证明成立的结果有8个,
∴摸出两张纸牌上的条件能证明成立的概率.
【点睛】本题考查的是全等三角形的判定以及用树状图法求概率,树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.1用树状图或表格求概率
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.甲、乙两人参加社会实践活动,随机选择“打扫社区卫生”和“参加社会调查”其中一项,那么两人同时选择“参加社会调查”的概率为( )
A. B. C. D.
2.有4张扑克牌如图所示,将其背面朝上,打乱顺序后放在桌面上.若从中随机抽取两张,则抽到的花色均为 (黑桃)的概率为( )
A. B. C. D.
3.一个不透明的袋中有四张完全相同的卡片,把它们分别标上数字1、2、3、4.随机抽取两张卡片,则两次抽取的卡片上数字之积为偶数的概率是( )
A. B. C. D.
4.为了疫情防控,某小区需要从甲、乙、丙、丁 4名志愿者中随机抽取2名负责该小区入口处的测温工作,则甲被抽中的概率是( )
A. B. C. D.
5.信阳是河南传统餐饮历史文化名城,信阳菜历经千年的积淀和发展,以鲜、香、爽、醇、中的独特味道传遍大江南北.某游客慕名而来,决定从“筒鲜鱼”“固始鹅块”“石凉粉”“罗山大肠汤”“闷罐肉”这5个特色美食中随机选取2 个进行品尝,则他抽到“筒鲜鱼”和“固始鹅块”的概率为( )
A. B. C. D.
6.一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3,随机摸出一个小球然后放回,再随机摸出一个小球,则两次摸出小球的标号相同的概率是( )
A. B. C. D.
7.某班甲、乙、丙、丁四个人站一横排照毕业相,则甲、乙两人恰好相邻的概率是( )
A. B. C. D.
8.在一个不透明的袋中装有2个黄球和2个红球,它们除颜色外没有其他区别,从袋中任意摸出一个球,然后放加搅匀,再从袋中任意摸一个球,那么两次都摸到黄球的概率是( )
A. B. C. D.
9.经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,那么两辆汽车经过这个十字路口时,第一辆车向左转,第二辆车向右转的概率是( ).
A. B. C. D.
10.在一个不透明的袋子中有3个白球、4个红球,这些球除颜色不同外其他完全相同.从袋子中随机摸出一个球,它是红球的概率是( )
A. B. C. D.
11.在“少年强则国强”这句话中,“强”字出现的频率是( )
A. B. C. D.
12.河南省有五处世界文化遗产:1.龙门石窟;2安阳殷墟;3.登封天地之中历史建筑群;4.大运河河南段;5.丝绸之路河南段.小明和小亮从中分别随机选取一个在五一期间参观,则正好选龙门石窟和安阳殷墟的概率为( )
A. B. C. D.
二、填空题
13.如图,开关,和处于断开状态,随机闭合开关,和中的两个,两盏灯同时发光的概率为 .
14.从一副54张牌的扑克牌中任取一张,它是梅花的概率是 .
15.邮票素有“国家名片”之称,方寸之间,包罗万象,为宣传北京2022年冬奥会,中国邮政发行了若干套冬奥会纪念邮票,其中有一套展现雪上运动的邮票,如图所示,某班级举行冬奥会有奖问答活动,在抢答环节中,若答对两题,可从4枚邮票中任意抽取2枚作为奖品,则恰好抽到“高山滑雪”和“自由式滑雪”的概率为 .
16.把一转盘先分成两个半圆,再把其中一个半圆等分成三等份,并标上数字如图所示,任意转动转盘,当转盘停止时,指针落在奇数区域的概率是 .
17.在一个不透明的袋子中有个除颜色外完全相同的小球,其中绿球个,红球个,摸出一个球不放回,混合均匀后再摸出一个球,两次都摸到红球的概率是 .
三、解答题
18.已知代数式.
(1)化简代数式;
(2)在满足的整数中随机抽取1个代入代数式中,求不会使得代数式无意义的概率.
19.根据教育部发布的《义务教育劳动课程标准(2022年版)》要求,2022年秋季开学起,劳动课将成为中小学生的一门独立课程.学期初清溪中学为了解本校学生对劳动课的重视程度,随机在校内调查了部分学生,调查结果分为“非常重视”“重视”“比较重视”“不重视”四类,并将结果绘制成如图所示的两幅不完整的统计图.根据图中信息,解答下列问题:
(1)在扇形统计图中,“非常重视”所占的圆心角的度数为__________,请补全条形统计图;
(2)对劳动课“非常重视”的4人中有一名男生,三名女生,若从中随机抽取两人作为“劳动教育宣传大使”,请利用画树状图法或列表法,求出恰好抽到的都是女生的概率.
20.某校为庆祝“五四青年节”,在2018年4月底组织该校学生举办了“传承五四精神共建和谐社土会”的演讲比赛.为了解学生在演讲比赛中的成绩情况,学校随机抽取了部分学生的演讲比赛成绩进行统计(满分:100分,等次:A.优秀:90~100分;B.良好:80﹣89分;C.一般:60﹣79分;D.较差:60分以下,不含60分)得到如下不完整的图表:
等次 频数 频率
A a 0.25
B b 0.5
C 3 m
D 2 0.1
根据以上信息解答下列问题
(1)表中a=_____,b=_____,m=_______,并补全频数分布直方图;
(2)根据抽查学生演讲成绩频数统计表制作的扇形统计图中,表示C等次部分的扇形中心角的度数是_______;
(3)若A等次中有2名女生,其余为男生,学校准备从A等次学生中抽取2名学生组成演讲组合参加全市“五四青年杯”演讲比赛,求恰好抽取1名男生和1名女生的概率.
21.为贯彻《教育部办公厅关于加强中小学生手机管理工作的通知》精神,某校团委组织了“我与手机说再见”为主题的演讲比赛,根据参赛同学的得分情况绘制了如图所示的两幅不完整的统计图(其中A表示“一等奖”,B表示“二等奖”,C表示“三等奖”,D表示“优秀奖”).
请你根据统计图中所提供的信息解答下列问题:
(1)获奖总人数为 人, ,A所对的圆心角度数是 °.
(2)请将条形统计图补充完整;
(3)学校将从获得一等奖的4名同学(其中有一名男生,三名女生)中随机抽取两名参加全市的比赛,请利用树状图或列表法求抽取同学中恰有一名男生和一名女生的概率.
22.人类活动对地球的环境产生影响,如“极端气候加剧、物种灭绝加速、海平面上升”等引发人们关注为了了解市民对“环境破坏成因”的认识,随机调查了部分市民,共有5个选项:A.滥伐森林;B.过度开矿;C.洞泽而“渔”;D.废物排弃;E其它.根据调查结果绘制了两幅不完整的统计图:
问题解决:
(1)本次调查活动中,调查的人数有______人,采取的调查方式是______(填上“普查”或“抽样调查”);
(2)在扇形统计图中,求“C”组所在扇形的圆心角的度数;
(3)若该市人口约有100万人,则可以估计其中持“D”组观点的市民人数约有______人:
(4)“保护生存环境建设美好家园”是实验学校开展环保类社团活动之宗旨,学校利用假期开设了四个如图所示的环保类社团项目,每人只能从这四个项目中随机选择一个项目,每一个项目被选择的可能性相同.小华和小聪分别从这四个项目中选择一个,请用列表或画树状图的方法,求小华和小聪选择同一个项目的概率.
社团名称 A(环保义工) B(绿植养护) C(回收材料) D(垃圾分类)
23.已知关于x的一元二次方程x2+bx+c=0.
(1)c=2b﹣1时,求证:方程一定有两个实数根.
(2)有甲、乙两个不透明的布袋,甲袋中装有3个除数字外完全相同的小球,分别标有数字1,2,3,乙袋中装有4个除数字外完全相同的小球,分别标有数字1,2,3,4,从甲袋中随机抽取一个小球,记录标有的数字为b,从乙袋中随机抽取一个小球,记录标有的数字为c,利用列表法或者树状图,求b、c的值使方程x2+bx+c=0有两个相等的实数根的概率.
24.新角度·概率、几何结合 如图(1),线段和相交于点C,连接.四张纸牌除正面分别写着如图(2)所示的四个不同的条件外完全相同,将四张纸牌背面朝上洗匀后放在桌面上.
(1)若小明第一次抽到纸牌③后,再从剩下的三张纸牌中随机抽取一张,则两张纸牌上的条件能证明成立的概率是_________;
(2)若从四张纸牌中随机抽出两张,求两张纸牌上的条件能证明成立的概率,先补全图(3)中的树状图,再计算.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B B D A C A A C B D
题号 11 12
答案 B B
1.B
【详解】试题解析:可能出现的结果
小明 打扫社区卫生 打扫社区卫生 参加社会调查 参加社会调查
小华 打扫社区卫生 参加社会调查 参加社会调查 打扫社区卫生
由上表可知,可能的结果共有种,且都是等可能的,其中两人同时选择“参加社会调查”的结果有种,
则所求概率
故选B.
点睛:求概率可以用列表法或者画树状图的方法.
2.B
【分析】本题主要考查了简单的概率计算,正确求出黑桃花色的概率是解题的关键.根据树状图列出所有的可能的结果,即可得到花色均为黑桃的概率.
【详解】解:设4张扑克牌为A,B,C,D,画树状图如图所示,
所有等可能情况数为12种,其中两张花色均为 (黑桃)的扑克牌有2种,
则抽到的花色均为 (黑桃)的概率为.
故选:B.
3.D
【分析】列举展示所有6种等可能的结果数,再找出两次抽取的卡片上数字之积为偶数的结果数,然后根据概率公式求解.
【详解】解:两次抽取的卡片上数字为:(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)
共有6种等可能的结果数,其中两次抽取的卡片上数字之积为偶数的结果数为5,
所以两次抽取的卡片上数字之积为偶数的概率=
故选D.
【点睛】本题考查了列表法与树状图法,解题关键在于利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.
4.A
【分析】根据题意画出树状图,然后求得全部情况的总数与符合条件的情况数目;二者的比值就是其发生的概率.
【详解】解:画树状图得:
∴一共有12种情况,抽取到甲的有6种,
∴P(抽到甲)= .
故选:A.
【点睛】本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,用到的知识点为:概率=所求情况数与总情况数之比.
5.C
【分析】通过列表法列出所有情况,再根据抽到“筒鲜鱼”和“固始鹅块”的情况数利用概率公式进行计算即可.
【详解】记“筒鲜鱼”“固始鹅块”“石凉粉”“罗山大肠汤”“闷罐肉”分别为A、B、C、D、E.抽到“筒鲜鱼”和“固始鹅块”即为AB或BA,则5个特色美食中随机选取2个进行品尝的所有可能情况列表为:
A B C D E
A AB AC AD AE
B AB BC BD BE
C AC BC CD CE
D AD BD CD DE
E AE BE CE DE
共有20种等可能事件,其中抽到AB或BA的有2种,
到AB或BA的概率为
即抽到“筒鲜鱼”和“固始鹅块”的概率为.
故选:C.
【点睛】本题考查了列表法或画树状图法求概率,即一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包括其中的m种结果,那么事件A发生的概率.
6.A
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的小球的标号相同的情况,再利用概率公式即可求得答案.
【详解】解:根据题意,画树状图如下:
共有9种等可能结果,其中两次摸出的小球的标号相同的有3种,
∴两次摸出的小球的标号相同的概率是,
故选:A.
【点睛】此题考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
7.A
【分析】根据列举法可进行求解概率.
【详解】解:由题意可知甲、乙、丙、丁排成一排的情况有:甲乙丙丁,甲乙丁丙,甲丙乙丁,甲丙丁乙,甲丁乙丙,甲丁丙乙,乙甲丙丁,乙甲丁丙,乙丙甲丁,乙丙丁甲,乙丁甲丙,乙丁丙甲,丙甲乙丁,丙甲丁乙,丙乙甲丁,丙乙丁甲,丙丁甲乙,丙丁乙甲,丁甲乙丙,丁甲丙乙,丁乙甲丙,丁乙丙甲,丁丙甲乙,丁丙乙甲,共24种,其中甲乙两人恰好相邻的有12种,所以甲、乙两人恰好相邻的概率是;
故选A.
【点睛】本题主要考查概率,熟练掌握概率的求解是解题的关键.
8.C
【分析】用树状图或列表法,列出所有等可能的情况数量n,找出符合题意的情况数量m,则概率为P= .
【详解】解:如下表:
第一次 第二次 黄球 黄球 红球 红球
黄球 (黄球,黄球) (黄球,黄球) (红球,黄球) (红球,黄球)
黄球 (黄球,黄球) (黄球,黄球) (红球,黄球) (红球,黄球)
红球 (黄球,红球) (黄球,红球) (红球,红球) (红球,红球)
红球 (黄球,红球) (黄球,红球) (红球,红球) (红球,红球)
一共有16种等可能的情况,
(黄球,黄球)的一共有4种,则两次都摸到黄球的概率P= ;
故选:C.
【点睛】考查列表法解决概率问题;找到两次都摸到黄球的情况数是解决本题的关键;用到的知识点为:概率等于所求情况数与总情况数之比.
9.B
【分析】根据题意可画出树状图,得到等可能的情况有9种,其中第一辆向左转,第二辆向右转的情况有1种,最后根据概率公式计算可得.
【详解】根据题意画出树状图如图所示,
由图可知这两辆汽车行驶方向共有9种等可能的情况,其中第一辆向左转,第二辆向右转的情况有1种,
∴第一辆向左转,第二辆向右转的概率为.
故选B.
【点睛】本题主要考查树状图法或列表法求概率.解题的关键是根据题意画出树状图或列出表格.
10.D
【分析】根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率,即可求出答案.
【详解】解:根据题意可得:袋子中有有3个白球,4个红球,共7个,
从袋子中随机摸出一个球,它是红色球的概率是;
故选:D.
【点睛】此题考查了概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.
11.B
【分析】这句话中总共6字,“强”出现了2次,则答案可求.
【详解】∵“少年强则国强”这句话共6个字,“强”出现了2次,
∴“强”字出现的频率是
故选:B.
【点睛】本题主要考查随机事件的概率,掌握概率公式是解题的关键.
12.B
【分析】本题主要考查了用树状图或列表法求概率,列出表格得出等可能情况,再找选中龙门石窟和安阳殷墟的情况,最后根据概率公式求解即可.
【详解】解:按照1.龙门石窟;2安阳殷墟;3.登封天地之中历史建筑群;4.大运河河南段;5.丝绸之路河南段.列表如下:
1 2 3 4 5
1 (1,1) (1,2) (1,3) (1,4) (1,5)
2 (2,1) (2,2) (2,3) (2,4) (2,5)
3 (3,1) (3,2) (3,3) (3,4) (3,5)
4 (4,1) (4,2) (4,3) (4,4) (4,5)
5 (5,1) (5,2) (5,3) (5,4) (5,5)
从列出中看,一共由25中等可能情况,选中1龙门石窟和2安阳殷墟的情况有2种,
故正好选龙门石窟和安阳殷墟的概率为:.
故选:B.
13.
【分析】本题主要考查了用树状图或列表法求等可能事件的概率,方法是用树状图或列表法列举出所有可能出现的结果总数,找出符合条件的结果数,用分数表示即可,注意每种情况发生的可能性相等.利用画树状图或列表的方法,得出所有可能出现的结果总数,从中找到符合条件的结果数,进而求出概率即可.
【详解】解:画树状图,如图所示:
∵共有6种等可能的结果,能让两盏灯泡同时发光的有2种情况,
∴能让两盏灯泡同时发光的概率为:.
14..
【分析】根据概率公式直接计算即可得到答案.
【详解】根据题意,一副54张牌的扑克牌中,是梅花的有13张梅花,
故从中任取一张牌刚好是梅花的概率是,
故答案为:.
【点睛】本题主要考查概率公式,掌握随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数是解题的关键.
15.
【分析】画树状图,共有12种等可能结果,其中恰好抽到“高山滑雪”和“自由式滑雪”的有2种结果,再由概率公式求解即可.
【详解】“越野滑雪”、“高山滑雪”、“冬季两项”、“自由式滑雪”分别记为甲、乙、丙、丁,
画树状图如下:
共有12种等可能结果,其中恰好抽到乙和丁即“高山滑雪”和“自由式滑雪”的有2种结果,
∴恰好抽到“高山滑雪”和“自由式滑雪”的概率为:.
【点睛】此题考查的是用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
16.
【分析】根据几何概率的求法:指针落在奇数区域的概率是就是所标数字为奇数的面积与总面积的比值.
【详解】解:观察这个图可知:所标数字为奇数的面积占总面积的,
∴指针落在奇数区域的概率是.
故答案为:.
【点睛】本题考查了几何概率的计算,理解并掌握“概率=相应的面积与总面积之比”是解题关键.
17.
【分析】运用画树状图的方法把所有等可能结果都表示出来,再运用概率的计算方法即可求解.
【详解】解:画树状图把所有等可能结果表示出来,
共有种等可能结果,其中两次摸到红球的结果有种,
∴两次都摸到红球的概率是,
故答案为:.
【点睛】本题主要列表法或画树状图法求随机事件的概率,掌握以上知识,数形结合分析是解题的关键.
18.(1)
(2)
【分析】(1)根据分式的混合运算法则计算即可解答;
(2)先求出满足的整数,再求出分式有意义的条件即可解答.
【详解】(1)解:
;
(2)解:在区间上的整数有,,0,1,2,共个,
由(1)得,分式有意义的条件为:且,即可取0,1,
∴不会使得代数式无意义的概率为.
【点睛】本题考查了分式的运算法则,分式有意义的条件及列举法求概率,解题的关键是熟练掌握以上知识点并保持计算准确.
19.(1)18°,见解析
(2)
【分析】(1)由“不重视”的人数和所占百分比可以求出抽查的总人数,再根据“比较重视”的人数即可得到其对应圆心角度数,用总人数减去已知三类的人数可以得到“重视”的人数,据此可以补全条形统计图;
(2)把三名女生分别记为,,,根据题意画出树状图即可得到解答.
【详解】(1)解: 调查的总人数为,
对劳动课“重视”的人数为,
,
补全条形统计图如下:
(2)解:画出树状图如下:
共有12种等可能的结果,其中抽到的都是女生的结果有6种,
所以恰好抽到的都是女生的概率为.
【点睛】本题考查数据的整理和分析,熟练掌握扇形统计图圆心角的求法、由样本所占百分比估计总体数量的方法、用列表法或树状图法求概率的方法是解题关键关键.
20.(1)5、10、0.15;(2)54°;(3).
【分析】(1)由D等次人数及其频率求得总人数,再根据“频率=频数÷总数”求解可得答案;
(2)用360°乘以C等次的频率即可得;
(3)列树形图后即可将所有情况全部列举出来,从而求得恰好抽中这两人的概率.
【详解】(1)∵被调查的总人数为2÷0.1=20,
∴a=20×0.25=5、b=20×0.5=10、m=3÷20=0.15,
补全图形如下:
故答案为5、10、0.15;
(2)表示C等次部分的扇形中心角的度数是360°×0.15=54°,
故答案为54°;
(3)画出树状图如下:
共有20种情况,其中“恰好是1名男生和1名女生”的情况有12种,
所以恰好是1名男生和1名女生的概率为=.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
21.(1)40,30,36
(2)见解析
(3)
【分析】(1)等级的人数除以所占的百分比,求出总人数,等级的人数除以总人数求出的值,等级所占的比例,求出圆心角;
(2)根据(1)中求出的等级的人数求出总人数;
(3)画出树状图进行求解即可.
【详解】(1)解:(人),等级的人数为:(人),
∴,
∴,
A所对的圆心角度数是;
故答案为:40,30,36;
(2)补全条形图如下:
(3)画出树状图如下:
共有12种等可能的结果,其中选择一男一女,共有6种等可能的结果,
∴.
【点睛】本题考查条形图和扇形图的综合应用,树状图法求概率.从统计图中有效的获取信息,是解题的关键.
22.(1)400,抽样调查
(2)
(3)30万
(4)
【分析】本题主要考查了扇形统计图与条形统计图信息相关联,树状图法或列表法求解概率,用样本估计总体:
(1)用A类别的人数除以其人数占比可以求出参与调查的人数,根据题意可知采用的是抽样调查方式;
(2)先求出B类别的人数,进而求出C类别的人数,再用360度乘以C类别的人数占比即可得到答案;
(3)用100万乘以样本中D类别的人数占比即可得到答案;
(4)先列表得到所有等可能性的结果数,再找到小华和小聪选择同一个项目的结果数,最后依据概率计算公式求解即可.
【详解】(1)解:人,
∴本次调查活动中,调查的人数有400人,
由题意得,采取的调查方式是抽样调查,
故答案为:400,抽样调查;
(2)解:B类别的人数为人,
∴C类别的人数为人,
∴在扇形统计图中,“”组所在扇形的圆心角等于;
(3)解:万人,
∴估计其中持“”组观点的市民人数约有30万人,
故答案为:30万;
(4)列表如下:
D
D
由表格可知共有16中等可能性的结果数,其中小华和小聪选择同一个项目的结果数有4种,
∴小华和小聪选择同一个项目的概率为.
23.(1)证明见解析;(2).
【分析】(1)把c=2b﹣1代入x2+bx+c=0.利用一元二次方程根的判别式即可得答案;
(2)根据方程x2+bx+c=0有两个相等的实数根,利用判别式可得b与c的关系,画出树状图,得出所有可能情况数及符合b与c的关系的情况数,利用概率公式即可得答案.
【详解】(1)∵c=2b﹣1,
∴x2+bx+c=x2+bx+2b=0.
∵==≥0,
∴方程一定有两个实数根.
(2)∵方程x2+bx+c=0有两个相等的实数根,
∴=0,
∴,
画树状图如下:
由树状图可知:所有可能情况数为12种,符合的情况数为2种,
∴b、c的值使方程x2+bx+c=0有两个相等的实数根的概率为=.
【点睛】本题考下一元二次方程的根的判别式及树状图法或列表法求概率,对于一元二次方程(),根的判别式为△=,当△>0时,方程有两个不相等的实数根,当△=0时,方程有两个相等的实数根,当△<0时,方程没有实数根;熟练掌握根的判别式及概率公式是解题关键.
24.(1)
(2)摸出两张纸牌上的条件能证明成立的概率.
【分析】(1)根据全等三角形的判定得到能证明成立的结果数,利用概率公式即可求解;
(2)补全树状图,共有12个可能的结果,根据全等三角形的判定得到能证明成立的结果数,即可得求出概率.
【详解】(1)解:∵,,
∴当抽中时,由能判断,①符合题意;
当抽中时,由能判断,②符合题意;
当抽中时,由不能判断,④不符合题意;
∴共有三种等可能结果,其中能证明成立的情况有2种
能证明概率是,
故答案为:;
(2)解:补全树状图,如图,
∵,
∴当抽中①,②,不能判断;
当抽中①,③,能判断;
当抽中①,④,能判断;
当抽中②,①,不能判断;
当抽中②,③,能判断;
当抽中②,④,能判断;
当抽中③,①,能判断;
当抽中③,②,能判断;
当抽中③,④,不能判断;
当抽中④,①,能判断;
当抽中④,②,能判断;
当抽中④,③,不能判断;
共有12个可能的结果,两张纸牌上的条件能证明成立的结果有8个,
∴摸出两张纸牌上的条件能证明成立的概率.
【点睛】本题考查的是全等三角形的判定以及用树状图法求概率,树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
