4.5相似三角形判定定理的证明同步练习(含解析)
文档属性
| 名称 | 4.5相似三角形判定定理的证明同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 849.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-15 08:22:57 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
4.5相似三角形判定定理的证明
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在□ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
A.3:2 B.1:1 C.2:5 D.2:3
2.下列条件中可以判定△ABC∽△A'B'C'的是( )
A. B.,∠B=∠B'
C.,∠A=∠A' D.
3.在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值为( )
A. B.2 C. D.1
4.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D是AB上的一个动点(不与A、B两点重合),DE⊥AC于点E,DF⊥BC于点F,点D从靠近点A的某一点向点B移动,矩形DECF的周长变化情况是( )
A.逐渐减小 B.逐渐增大 C.先增大后减小 D.先减小后增大
5.已知,如图所示的一张三角形纸片ABC,边AB的长为20cm,AB边上的高为25cm,在三角形纸片ABC中从下往上依次裁剪去宽为4cm的矩形纸条,若剪得的其中一张纸条是正方形,那么这张正方形纸条是( )
A.第4张 B.第5张 C.第6张 D.第7张
6.如图,在平行四边形ABCD中,E、F分别是BC边,CD边的中点,AE、AF分别交BD于点G,H,设△AGH的面积为S1,平行四边形ABCD的面积为S2,则S1:S2的值为( )
A. B. C. D.
7.如图,中,、是边上的点,,在边上,,交,于,,则等于( ).
A. B. C. D.
8.在平面直角坐标系中,第一个正方形ABCD的位置如图6所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…按这样的规律进行下去,第2010个正方形的面积为( )
A. B. C. D.
9.如图,D,E分别是△ABC的边AB,AC上的点,且DE∥BC,AD=2,DB=3,△ADE的面是2,则四边形BCED的面积是( )
A.4 B.8 C. D.
10.如图,△ABC的面积为60,点G是重心,连结BG并延长交AC于D,连结GA,则△GAB的面积为( )
A.40 B.30 C.20 D.10
11.如图,∠ACB=∠ADC=90°,BC=a,AC=b,AD=c,要使⊿ABC∽⊿CAD,只要CD等于( )
A. B. C. D.
12.如图,DE∥BC,且AD=4,DB=2,DE=3.5,则BC的长度为( )
A.5.5 B.5.25 C.6.5 D.7
二、填空题
13.在中,,是的中点,过点作直线,使截得的三角形与原三角形相似,这样的直线有 条.
14.如图,△ABC内接于⊙O,D是弧BC的中点,OD交BC于点H,且OH=DH,连接AD,过点B作BE⊥AD于点E,连接EH,BF⊥AC于M,若AC=5,EH=,则AF= .
15.已知:在平行四边形ABCD中,点E在DA的延长线上,AE=AD,连接CE交BD于点F,则的值是 .
16.如图,在边长为2的正方形ABCD中,P是BC边上一动点(点P不与B、C重合),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA、NA,则以下结论:①△CMP∽△BPA;②四边形AMCB的面积最大值为2.5;③△ADN≌△AEN;④线段AM的最小值为2.5;⑤当P为BC中点时,AE为线段NP的中垂线.正确的有 (只填序号)
17.如图,直角梯形ABCD中,AD∥BC,AC⊥AB,AD=8,BC=10,则梯形ABCD面积是 .
三、解答题
18.阅读下面材料.
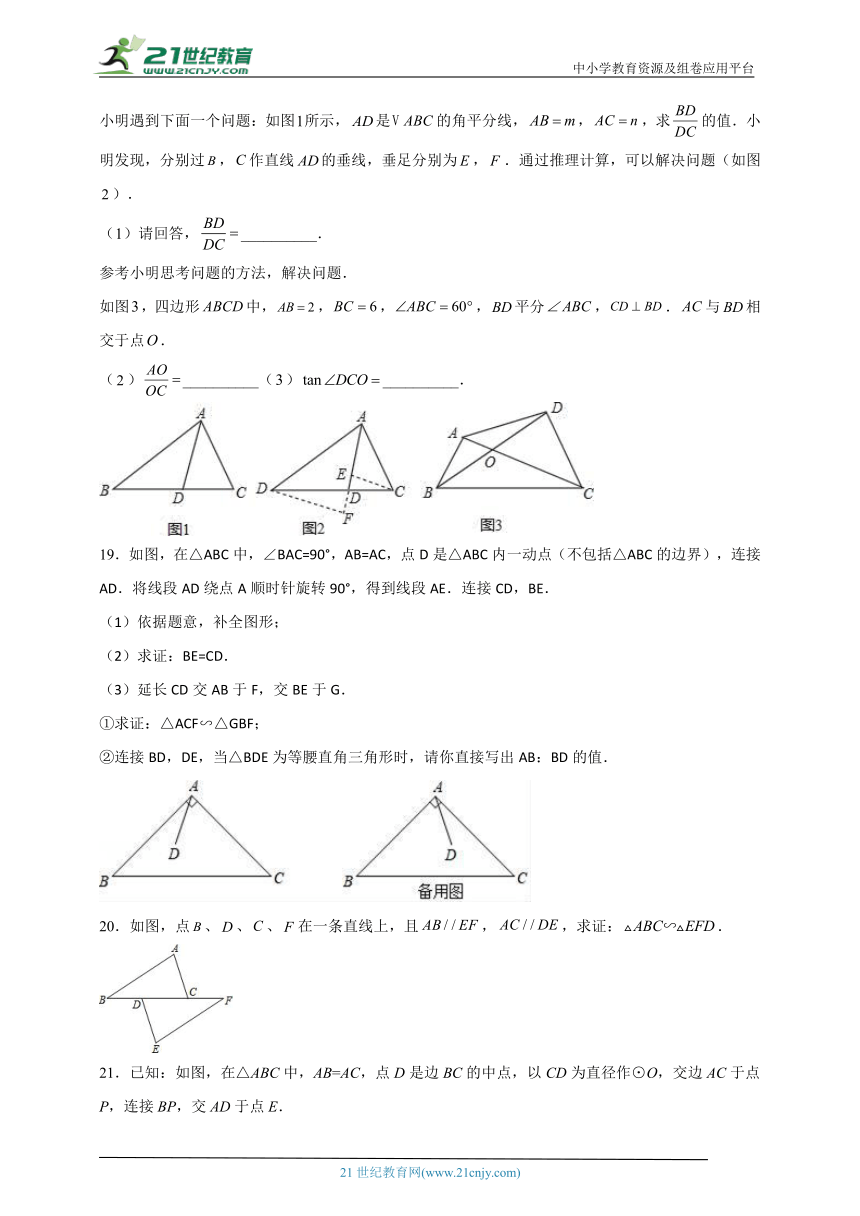
小明遇到下面一个问题:如图所示,是的角平分线,,,求的值.小明发现,分别过,作直线的垂线,垂足分别为,.通过推理计算,可以解决问题(如图).
()请回答,__________.
参考小明思考问题的方法,解决问题.
如图,四边形中,,,,平分,.与相交于点.
()__________()__________.
19.如图,在△ABC中,∠BAC=90°,AB=AC,点D是△ABC内一动点(不包括△ABC的边界),连接AD.将线段AD绕点A顺时针旋转90°,得到线段AE.连接CD,BE.
(1)依据题意,补全图形;
(2)求证:BE=CD.
(3)延长CD交AB于F,交BE于G.
①求证:△ACF∽△GBF;
②连接BD,DE,当△BDE为等腰直角三角形时,请你直接写出AB:BD的值.
20.如图,点、、、在一条直线上,且,,求证:.
21.已知:如图,在△ABC中,AB=AC,点D是边BC的中点,以CD为直径作⊙O,交边AC于点P,连接BP,交AD于点E.
(1)求证:AD是⊙O的切线;
(2)如果PB是⊙O的切线,BC=4,求PE的长.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D C A A B A D D C C
题号 11 12
答案 D B
1.D
【详解】∵DE∥AB,
∴△DEF∽△BAF,
∴,
∴,
∴.
故选D.
2.C
【分析】判定两个三角形相似,可用两个对应角相等,也可以是边长对应成比例,但必须夹角相等.
【详解】、中只有对应边成比例,角不确定,、错,
中不是、的夹角,所以错,
中对应边成比例,且夹角相等,所以可判定其相似,对.
故选:.
【点睛】题中对应线段成比例,、中没有角的关系,而中不是、的夹角,做题时应注意.
3.A
【详解】试题分析:设AP=x,PD=4﹣x.
∵∠EAP=∠EAP,∠AEP=∠ADC;
∴△AEP∽△ADC,故=①;
同理可得△DFP∽△DAB,故=②.
①+②得=,
∴PE+PF=.故选A.
考点:矩形的性质;相似三角形的判定与性质.
点评:此题比较简单,根据矩形的性质及相似三角形的性质解答即可.
4.A
【详解】试题解析:设DE=λ,DF=μ;
∵DE⊥AC于点E,DF⊥BC于点F,
∴四边形DECF为矩形,
∴CF=DE=λ,CE=DF=μ,
∴矩形DECF的周长η=2λ+2μ;
∵DE∥BC,
∴△ADE∽△ABC,
∴①;同理可证②,
由①+②得:,
∴μ=8-
∴
=-+16,
∵-<0,
∴随λ的增大而减小;
∵点D从靠近点A的某一点向点B移动时,λ逐渐变大,
∴矩形DECF的周长η逐渐减小.
故选A.
考点:相似三角形的判定与性质.
5.B
【详解】试题分析:根据相似三角形的相似比求得顶点到这个正方形的长,再根据矩形的宽求得是第几张.
解:已知剪得的纸条中有一张是正方形,则正方形中平行于底边的边是4,
所以根据相似三角形的性质可设从顶点到这个正方形的线段为x,
则4:20=x:25,
解得x=5,
所以另一段长为25 5=20,
因为20÷4=5,所以是第5张.
故选B.
点睛:本题是一道动手操作题.主要涉及的知识点是相似三角形的性质.解题的关键在于要在理解题意的基础上,运用相似三角形的性质建立方程求解.
6.A
【分析】由平行可得,,从而得到对应线段成比例,推得BG=GH=DH,最后利用等底等高的三角形面积相等推理得解.
【详解】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AB=CD,AD=BC,
∴ , ,
,
同理,,
∵DF=CF,BE=CE,
∴ ,
∴ ,
∴BG=GH=DH,
∵△AGH的面积为S1,
∴S△ABG=S△AGH=S△ADH=S1,
∴S平行四边形ABCD=6S1,
∴S1:S2,=1:6,
故选A.
【点睛】本题考查平行线分线段成比例定理,灵活转移线段的条件是解题的关键.
7.D
【详解】试题解析:连接EM,
CE:CD=CM:CA=1:3
∴EM平行于AD
∴△BHD∽△BME,△CEM∽△CDA
∴HD:ME=BD:BE=3:5,ME:AD=CM:AC=1:3
∴AH:ME=12:5
∴HG:GM=AH:EM=12:5
设GM=5k,GH=12k,
∵BH:HM=3:2=BH:17k
故选D.
8.D
【详解】分析:分别求出第1个,第3个,第3个,第4个正方形的边长和面积,从它们的表达式中探索规律.
详解:
正方形序号 边长 面积
1 5
2 5()2
3 5[()2]2
4 5[()3]2
n …… 5[()n-1]2
所以第2010个正方形的面积为5[()2010-1]2=5()4018.
点睛:解规律探索题要注意以下两点:(1)探索规律的关键:注意观察已知的对应数值(图形)的变化规律,从中发现数量关系或图形的变化规律,即得到规律.(2)探索规律的步骤:①从具体的题目出发,用列表或列举的方式,把数量或图形的变化特点展现在图表当中;②认真观察图表或图形,通过合理联想,大胆猜想,总结归纳,得出数字或图形间的变化规律,形成结论;③由此及彼验证结论的正误.
9.C
【详解】解:∵DE∥BC,∴△ADE∽△ABC,∴,∵AD=2,DB=3,∴,∴,∵△ADE的面积是2,∴△ABC的面积是12.5,∴四边形BCED的面积是12.5﹣2=10.5,故选C.
点睛:本题考查了相似三角形的判定和性质,注意:相似三角形的面积之比=相似比的平方.
10.C
【详解】试题解析:连接CG并延长交AB于点E,
∵G是△ABC的重心,
故选C.
11.D
【详解】试题解析:假设△ABC∽△CAD,
∴,
即CD=,
∴要使△ABC∽△CAD,只要CD等于,
故选D.
12.B
【详解】如图,DE∥BC,即可得△ADE∽△ABC,根据相似三角形的性质可得,即,解得BC=5.25,故选B.
13.
【分析】本题主要应用两三角形相似的判定定理,做题即可.
【详解】作DE∥AB,DF∥BC,可得相似,
作∠CDG=∠B,∠ADH=∠C,也可得相似三角形.
所以可作4条.
故答案为4.
【点睛】考查相似三角形的判定,掌握相似三角形的4中判定方法是解题的关键.
14.
【详解】如图,延长BE交AC的延长线于N,连接OB、OC、BD.
∵,
∴∠EAB=∠EAN,
∵AD⊥BN,
∴∠AEB=∠AEN=90°,
∴∠ABE+∠BAE=90°,∠N+∠EAN=90°,
∴∠ABE=∠N,
∴AB=AN,
∴BE=EN,
∵OD⊥BC,
∴BH=HC,
∴CN=2EH,
∴AB=AN=AC+CN=8,
∵OH=HD,BH⊥OD,
∴BO=BD=OD,
∴∠BOD=∠DOC=60°,
∴∠BAC=∠BOC=60°,
在Rt△AMB中,AM=AB=4,BM=4,
在Rt△BMC中,BC=,
∵∠MAF=∠MBC,∠AMF=∠BMC,
∴△AMF∽△BMC,
∴,
∴,
∴AF=.
故答案为.
【点睛】考查了圆周角定理、垂径定理、全等三角形的判定、勾股定理,相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,注意掌握数形结合思想的应用.
15.;
【详解】分析:首先设AE=x,则BC=AD=2x,DE=3x,根据△BCF和△DEF相似得出答案.
详解:设AE=x,∵AE=AD,∴BC=AD=2x,DE=3x,
∵DE∥BC, ∴△BCF∽△DEF, ∴.
点睛:本题主要考查的是三角形相似的判定与性质,属于基础题型.判定三角形相似是解题的关键.
16.①②③④
【分析】①正确.只要证明∠CPM=∠PAB,∠C=∠B=90°,即可;②正确,设PB=x,构建二次函数,利用二次函数性质解决问题即可;③正确.根据HL即可证明;④正确,作MG⊥AB于G,因为AM= ,所以AG最小时AM最小,构建二次函数,求得AG的最小值为 ,AM的最小值为 .⑤错误,设ND=NE=y,在Rt△PCN中,利用勾股定理求出y即可解决问题.
【详解】①由翻折可知,∠APE=∠APB,∠MPC=∠MPN,
∴∠APE+∠MPF=∠CPN+∠BPE=90°,
∴∠CPM+∠APB=90°,∵∠APB+∠PAB=90°,
∴∠CPM=∠PAB,∵∠C=∠B=90°,
∴△CMP∽△BPA.故①正确;
②设PB=x,则CP=2-x,
∵△CMP∽△BPA,
∴,,
∴CM=x(2-x),
∴S四边形AMCB= [2+x(2-x)]×2=-x2+x+2=-(x-1)2+2.5,
∴x=1时,四边形AMCB面积最大值为2.5,故②正确;
③在Rt△ADN和Rt△AEN中,
,
∴△ADN≌△AEN.故③正确;
④作MG⊥AB于G,
∵AM=,
∴AG最小时AM最小,
∵AG=AB-BG=AB-CM=2-x(2-x)=(x-1)2+,
∴x=1时,AG最小值=,
∴AM的最小值=,故④正确.
⑤当PB=PC=PE=1时,
由折叠知,ND=NE,
设ND=NE=y,
在Rt△PCN中,(y+1)2=(2-y)2+12解得y=
∴NE=,
∴NE≠EP,故⑤错误,
故填:①②③④
【点睛】此题是四边形综合题主要考查了正方形的性质、相似三角形的判定和性质、全等三角形的性质、勾股定理等知识,解题的关键是学会构建二次函数解决最值问题,学会添加常用辅助线,属于中考压轴题.
17.36
【详解】分析:由已知条件易证得△ABC∽△DCA,可得即在中,由勾股定理可得通过两式可求得的长,再根据梯形的面积公式求解即可.
详解:∵AD∥BC,
∴∠ACB=∠DAC,
∵
∴△ABC∽△DCA,
∴ 即
∵在中,
∴
∴梯形的面积
故答案为:36.
点睛:考查了梯形的性质和面积公式,相似三角形的判定与性质,勾股定理等知识点,属于中档题,考查了学生综合知识的运用,正确求得梯形的高是解题的关键.
18.(1).
(2).
(3).
【详解】()根据小明的结论得===;
(2)作AE⊥BD于E,证明△AOE∽△COD,求出AE、BE、DE、OD的长即可求出tan∠DCO的值.
解:()∵.
().
()作于.
∵,.∴,∴.
∴.
∵,∴.
∵平分,
∴.
∴.
又∵,
∴,.
∴.
∴.
19.(1);(2)证明见解析;(3)①证明见解析,②AB:BD=:2或:2.
【分析】(1)根据题意,将AD绕点A顺时针旋转90°,补全图形即可;
(2)已知AD=AE,∠BAD+∠BAE=∠BAD+∠CAD,可得∠BAE=∠CAD,利用全等三角形判定依据SAS,即可求证本问结论;
(3)①利用全等三角形对应角相等得到∠ACD=∠ABE,由对顶角相等得到∠AFC=∠GFB,至此问题不难证明;
②分为∠EDB=90°与∠BED=90°时两种情况,分别利用△AED、△EBD、△ABC为等腰直角三角形,即直角三角形斜边等于直角边的倍,结合BE=CD,求解直角三角形,即可得解.
【详解】(1)解:图形如图所示:
(2)证明:∵∠EAD=∠BAC=90°,
∴∠EAB=∠DAC,
∵AE=AD,AB=AC,
∴△EAB≌△DAC,
∴BE=CD.
(3)①证明:∵△EAB≌△DAC,
∴∠ABE=∠ACD,
∵∠CFA=∠BFG,
∴△ACF∽△GBF.
②如图2中,当BE=ED,∠BED=90°时,设AE=AD=a,则DE=BE=a,BD=BE=2a,
∵∠ADE=∠BDE=45°,
∴∠ADB=90°,
∴AB==a,
∴AB:BD=a:2a=:2.
如图3中,当BD=DE,∠BDE=90°时,设AE=AD=a,则BD=DE=a,BE=2a,
∵∠AED=∠BED=45°,
∴∠AEB=90°,
∴AB=a,
∴AB:BD=a:a=:2.
【点睛】本题考查了旋转的性质,相似三角形的判定,全等三角形的判定与性质,等腰直角三角形的性质 ,勾股定理等知识及分类讨论的数学思想.解(2)的关键是熟练掌握全等三角形的判定与性质,解(3)①的关键是熟练掌握相似三角形的判定方法,解(3)②的关键是分两种情况进行讨论.
20.见解析
【分析】,,根据平行线的性质得到,,根据两组角对应相等的两个三角形相似即可判定.
【详解】证明:∵,,
∴,,
∴.
【点睛】此题考查了相似三角形的判定,常用的判定方法有:
①有两个对应角相等的三角形相似;
②有两组对应边的比相等,且其夹角相等,则两个三角形相似;
③三组对应边的比相等,则两个三角形相似.
21.(1) 证明见解析;(2).
【详解】试题分析:
(1)由AB=AC,点D是BC的中点可得AD⊥BC,结合CD是⊙O的直径,即可得AD是⊙O的切线;
(2)连接OP,由已知易求得BD、OB、OP和BP的长,再证PE=DE,△BDE∽△BPO即可列出比例式求得DE的长,从而可得PE的长.
试题解析:
(1)∵AB=AC,点D是边BC的中点,
∴AD⊥CD,
∵CD为⊙O的直径,
∴AD是⊙O的切线;
(2)连接OP,
∵点D是边BC的中点,BC=4,CD是⊙O的直径,
∴CD=BD=2,OP=1,OB=3,
∴在Rt△BOP中,BP=,
∵AD是⊙O的切线,PB是⊙O的切线,
∴PE=DE,∠BPO=90°,
∵AD⊥CD,
∴∠ADB=∠BPO=90°,
又∵∠DBE=∠PBO,
∴△BDE∽△BPO,
∴,即,解得:DE=,
∴PE=DE=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.5相似三角形判定定理的证明
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在□ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
A.3:2 B.1:1 C.2:5 D.2:3
2.下列条件中可以判定△ABC∽△A'B'C'的是( )
A. B.,∠B=∠B'
C.,∠A=∠A' D.
3.在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值为( )
A. B.2 C. D.1
4.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D是AB上的一个动点(不与A、B两点重合),DE⊥AC于点E,DF⊥BC于点F,点D从靠近点A的某一点向点B移动,矩形DECF的周长变化情况是( )
A.逐渐减小 B.逐渐增大 C.先增大后减小 D.先减小后增大
5.已知,如图所示的一张三角形纸片ABC,边AB的长为20cm,AB边上的高为25cm,在三角形纸片ABC中从下往上依次裁剪去宽为4cm的矩形纸条,若剪得的其中一张纸条是正方形,那么这张正方形纸条是( )
A.第4张 B.第5张 C.第6张 D.第7张
6.如图,在平行四边形ABCD中,E、F分别是BC边,CD边的中点,AE、AF分别交BD于点G,H,设△AGH的面积为S1,平行四边形ABCD的面积为S2,则S1:S2的值为( )
A. B. C. D.
7.如图,中,、是边上的点,,在边上,,交,于,,则等于( ).
A. B. C. D.
8.在平面直角坐标系中,第一个正方形ABCD的位置如图6所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…按这样的规律进行下去,第2010个正方形的面积为( )
A. B. C. D.
9.如图,D,E分别是△ABC的边AB,AC上的点,且DE∥BC,AD=2,DB=3,△ADE的面是2,则四边形BCED的面积是( )
A.4 B.8 C. D.
10.如图,△ABC的面积为60,点G是重心,连结BG并延长交AC于D,连结GA,则△GAB的面积为( )
A.40 B.30 C.20 D.10
11.如图,∠ACB=∠ADC=90°,BC=a,AC=b,AD=c,要使⊿ABC∽⊿CAD,只要CD等于( )
A. B. C. D.
12.如图,DE∥BC,且AD=4,DB=2,DE=3.5,则BC的长度为( )
A.5.5 B.5.25 C.6.5 D.7
二、填空题
13.在中,,是的中点,过点作直线,使截得的三角形与原三角形相似,这样的直线有 条.
14.如图,△ABC内接于⊙O,D是弧BC的中点,OD交BC于点H,且OH=DH,连接AD,过点B作BE⊥AD于点E,连接EH,BF⊥AC于M,若AC=5,EH=,则AF= .
15.已知:在平行四边形ABCD中,点E在DA的延长线上,AE=AD,连接CE交BD于点F,则的值是 .
16.如图,在边长为2的正方形ABCD中,P是BC边上一动点(点P不与B、C重合),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA、NA,则以下结论:①△CMP∽△BPA;②四边形AMCB的面积最大值为2.5;③△ADN≌△AEN;④线段AM的最小值为2.5;⑤当P为BC中点时,AE为线段NP的中垂线.正确的有 (只填序号)
17.如图,直角梯形ABCD中,AD∥BC,AC⊥AB,AD=8,BC=10,则梯形ABCD面积是 .
三、解答题
18.阅读下面材料.
小明遇到下面一个问题:如图所示,是的角平分线,,,求的值.小明发现,分别过,作直线的垂线,垂足分别为,.通过推理计算,可以解决问题(如图).
()请回答,__________.
参考小明思考问题的方法,解决问题.
如图,四边形中,,,,平分,.与相交于点.
()__________()__________.
19.如图,在△ABC中,∠BAC=90°,AB=AC,点D是△ABC内一动点(不包括△ABC的边界),连接AD.将线段AD绕点A顺时针旋转90°,得到线段AE.连接CD,BE.
(1)依据题意,补全图形;
(2)求证:BE=CD.
(3)延长CD交AB于F,交BE于G.
①求证:△ACF∽△GBF;
②连接BD,DE,当△BDE为等腰直角三角形时,请你直接写出AB:BD的值.
20.如图,点、、、在一条直线上,且,,求证:.
21.已知:如图,在△ABC中,AB=AC,点D是边BC的中点,以CD为直径作⊙O,交边AC于点P,连接BP,交AD于点E.
(1)求证:AD是⊙O的切线;
(2)如果PB是⊙O的切线,BC=4,求PE的长.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D C A A B A D D C C
题号 11 12
答案 D B
1.D
【详解】∵DE∥AB,
∴△DEF∽△BAF,
∴,
∴,
∴.
故选D.
2.C
【分析】判定两个三角形相似,可用两个对应角相等,也可以是边长对应成比例,但必须夹角相等.
【详解】、中只有对应边成比例,角不确定,、错,
中不是、的夹角,所以错,
中对应边成比例,且夹角相等,所以可判定其相似,对.
故选:.
【点睛】题中对应线段成比例,、中没有角的关系,而中不是、的夹角,做题时应注意.
3.A
【详解】试题分析:设AP=x,PD=4﹣x.
∵∠EAP=∠EAP,∠AEP=∠ADC;
∴△AEP∽△ADC,故=①;
同理可得△DFP∽△DAB,故=②.
①+②得=,
∴PE+PF=.故选A.
考点:矩形的性质;相似三角形的判定与性质.
点评:此题比较简单,根据矩形的性质及相似三角形的性质解答即可.
4.A
【详解】试题解析:设DE=λ,DF=μ;
∵DE⊥AC于点E,DF⊥BC于点F,
∴四边形DECF为矩形,
∴CF=DE=λ,CE=DF=μ,
∴矩形DECF的周长η=2λ+2μ;
∵DE∥BC,
∴△ADE∽△ABC,
∴①;同理可证②,
由①+②得:,
∴μ=8-
∴
=-+16,
∵-<0,
∴随λ的增大而减小;
∵点D从靠近点A的某一点向点B移动时,λ逐渐变大,
∴矩形DECF的周长η逐渐减小.
故选A.
考点:相似三角形的判定与性质.
5.B
【详解】试题分析:根据相似三角形的相似比求得顶点到这个正方形的长,再根据矩形的宽求得是第几张.
解:已知剪得的纸条中有一张是正方形,则正方形中平行于底边的边是4,
所以根据相似三角形的性质可设从顶点到这个正方形的线段为x,
则4:20=x:25,
解得x=5,
所以另一段长为25 5=20,
因为20÷4=5,所以是第5张.
故选B.
点睛:本题是一道动手操作题.主要涉及的知识点是相似三角形的性质.解题的关键在于要在理解题意的基础上,运用相似三角形的性质建立方程求解.
6.A
【分析】由平行可得,,从而得到对应线段成比例,推得BG=GH=DH,最后利用等底等高的三角形面积相等推理得解.
【详解】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AB=CD,AD=BC,
∴ , ,
,
同理,,
∵DF=CF,BE=CE,
∴ ,
∴ ,
∴BG=GH=DH,
∵△AGH的面积为S1,
∴S△ABG=S△AGH=S△ADH=S1,
∴S平行四边形ABCD=6S1,
∴S1:S2,=1:6,
故选A.
【点睛】本题考查平行线分线段成比例定理,灵活转移线段的条件是解题的关键.
7.D
【详解】试题解析:连接EM,
CE:CD=CM:CA=1:3
∴EM平行于AD
∴△BHD∽△BME,△CEM∽△CDA
∴HD:ME=BD:BE=3:5,ME:AD=CM:AC=1:3
∴AH:ME=12:5
∴HG:GM=AH:EM=12:5
设GM=5k,GH=12k,
∵BH:HM=3:2=BH:17k
故选D.
8.D
【详解】分析:分别求出第1个,第3个,第3个,第4个正方形的边长和面积,从它们的表达式中探索规律.
详解:
正方形序号 边长 面积
1 5
2 5()2
3 5[()2]2
4 5[()3]2
n …… 5[()n-1]2
所以第2010个正方形的面积为5[()2010-1]2=5()4018.
点睛:解规律探索题要注意以下两点:(1)探索规律的关键:注意观察已知的对应数值(图形)的变化规律,从中发现数量关系或图形的变化规律,即得到规律.(2)探索规律的步骤:①从具体的题目出发,用列表或列举的方式,把数量或图形的变化特点展现在图表当中;②认真观察图表或图形,通过合理联想,大胆猜想,总结归纳,得出数字或图形间的变化规律,形成结论;③由此及彼验证结论的正误.
9.C
【详解】解:∵DE∥BC,∴△ADE∽△ABC,∴,∵AD=2,DB=3,∴,∴,∵△ADE的面积是2,∴△ABC的面积是12.5,∴四边形BCED的面积是12.5﹣2=10.5,故选C.
点睛:本题考查了相似三角形的判定和性质,注意:相似三角形的面积之比=相似比的平方.
10.C
【详解】试题解析:连接CG并延长交AB于点E,
∵G是△ABC的重心,
故选C.
11.D
【详解】试题解析:假设△ABC∽△CAD,
∴,
即CD=,
∴要使△ABC∽△CAD,只要CD等于,
故选D.
12.B
【详解】如图,DE∥BC,即可得△ADE∽△ABC,根据相似三角形的性质可得,即,解得BC=5.25,故选B.
13.
【分析】本题主要应用两三角形相似的判定定理,做题即可.
【详解】作DE∥AB,DF∥BC,可得相似,
作∠CDG=∠B,∠ADH=∠C,也可得相似三角形.
所以可作4条.
故答案为4.
【点睛】考查相似三角形的判定,掌握相似三角形的4中判定方法是解题的关键.
14.
【详解】如图,延长BE交AC的延长线于N,连接OB、OC、BD.
∵,
∴∠EAB=∠EAN,
∵AD⊥BN,
∴∠AEB=∠AEN=90°,
∴∠ABE+∠BAE=90°,∠N+∠EAN=90°,
∴∠ABE=∠N,
∴AB=AN,
∴BE=EN,
∵OD⊥BC,
∴BH=HC,
∴CN=2EH,
∴AB=AN=AC+CN=8,
∵OH=HD,BH⊥OD,
∴BO=BD=OD,
∴∠BOD=∠DOC=60°,
∴∠BAC=∠BOC=60°,
在Rt△AMB中,AM=AB=4,BM=4,
在Rt△BMC中,BC=,
∵∠MAF=∠MBC,∠AMF=∠BMC,
∴△AMF∽△BMC,
∴,
∴,
∴AF=.
故答案为.
【点睛】考查了圆周角定理、垂径定理、全等三角形的判定、勾股定理,相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,注意掌握数形结合思想的应用.
15.;
【详解】分析:首先设AE=x,则BC=AD=2x,DE=3x,根据△BCF和△DEF相似得出答案.
详解:设AE=x,∵AE=AD,∴BC=AD=2x,DE=3x,
∵DE∥BC, ∴△BCF∽△DEF, ∴.
点睛:本题主要考查的是三角形相似的判定与性质,属于基础题型.判定三角形相似是解题的关键.
16.①②③④
【分析】①正确.只要证明∠CPM=∠PAB,∠C=∠B=90°,即可;②正确,设PB=x,构建二次函数,利用二次函数性质解决问题即可;③正确.根据HL即可证明;④正确,作MG⊥AB于G,因为AM= ,所以AG最小时AM最小,构建二次函数,求得AG的最小值为 ,AM的最小值为 .⑤错误,设ND=NE=y,在Rt△PCN中,利用勾股定理求出y即可解决问题.
【详解】①由翻折可知,∠APE=∠APB,∠MPC=∠MPN,
∴∠APE+∠MPF=∠CPN+∠BPE=90°,
∴∠CPM+∠APB=90°,∵∠APB+∠PAB=90°,
∴∠CPM=∠PAB,∵∠C=∠B=90°,
∴△CMP∽△BPA.故①正确;
②设PB=x,则CP=2-x,
∵△CMP∽△BPA,
∴,,
∴CM=x(2-x),
∴S四边形AMCB= [2+x(2-x)]×2=-x2+x+2=-(x-1)2+2.5,
∴x=1时,四边形AMCB面积最大值为2.5,故②正确;
③在Rt△ADN和Rt△AEN中,
,
∴△ADN≌△AEN.故③正确;
④作MG⊥AB于G,
∵AM=,
∴AG最小时AM最小,
∵AG=AB-BG=AB-CM=2-x(2-x)=(x-1)2+,
∴x=1时,AG最小值=,
∴AM的最小值=,故④正确.
⑤当PB=PC=PE=1时,
由折叠知,ND=NE,
设ND=NE=y,
在Rt△PCN中,(y+1)2=(2-y)2+12解得y=
∴NE=,
∴NE≠EP,故⑤错误,
故填:①②③④
【点睛】此题是四边形综合题主要考查了正方形的性质、相似三角形的判定和性质、全等三角形的性质、勾股定理等知识,解题的关键是学会构建二次函数解决最值问题,学会添加常用辅助线,属于中考压轴题.
17.36
【详解】分析:由已知条件易证得△ABC∽△DCA,可得即在中,由勾股定理可得通过两式可求得的长,再根据梯形的面积公式求解即可.
详解:∵AD∥BC,
∴∠ACB=∠DAC,
∵
∴△ABC∽△DCA,
∴ 即
∵在中,
∴
∴梯形的面积
故答案为:36.
点睛:考查了梯形的性质和面积公式,相似三角形的判定与性质,勾股定理等知识点,属于中档题,考查了学生综合知识的运用,正确求得梯形的高是解题的关键.
18.(1).
(2).
(3).
【详解】()根据小明的结论得===;
(2)作AE⊥BD于E,证明△AOE∽△COD,求出AE、BE、DE、OD的长即可求出tan∠DCO的值.
解:()∵.
().
()作于.
∵,.∴,∴.
∴.
∵,∴.
∵平分,
∴.
∴.
又∵,
∴,.
∴.
∴.
19.(1);(2)证明见解析;(3)①证明见解析,②AB:BD=:2或:2.
【分析】(1)根据题意,将AD绕点A顺时针旋转90°,补全图形即可;
(2)已知AD=AE,∠BAD+∠BAE=∠BAD+∠CAD,可得∠BAE=∠CAD,利用全等三角形判定依据SAS,即可求证本问结论;
(3)①利用全等三角形对应角相等得到∠ACD=∠ABE,由对顶角相等得到∠AFC=∠GFB,至此问题不难证明;
②分为∠EDB=90°与∠BED=90°时两种情况,分别利用△AED、△EBD、△ABC为等腰直角三角形,即直角三角形斜边等于直角边的倍,结合BE=CD,求解直角三角形,即可得解.
【详解】(1)解:图形如图所示:
(2)证明:∵∠EAD=∠BAC=90°,
∴∠EAB=∠DAC,
∵AE=AD,AB=AC,
∴△EAB≌△DAC,
∴BE=CD.
(3)①证明:∵△EAB≌△DAC,
∴∠ABE=∠ACD,
∵∠CFA=∠BFG,
∴△ACF∽△GBF.
②如图2中,当BE=ED,∠BED=90°时,设AE=AD=a,则DE=BE=a,BD=BE=2a,
∵∠ADE=∠BDE=45°,
∴∠ADB=90°,
∴AB==a,
∴AB:BD=a:2a=:2.
如图3中,当BD=DE,∠BDE=90°时,设AE=AD=a,则BD=DE=a,BE=2a,
∵∠AED=∠BED=45°,
∴∠AEB=90°,
∴AB=a,
∴AB:BD=a:a=:2.
【点睛】本题考查了旋转的性质,相似三角形的判定,全等三角形的判定与性质,等腰直角三角形的性质 ,勾股定理等知识及分类讨论的数学思想.解(2)的关键是熟练掌握全等三角形的判定与性质,解(3)①的关键是熟练掌握相似三角形的判定方法,解(3)②的关键是分两种情况进行讨论.
20.见解析
【分析】,,根据平行线的性质得到,,根据两组角对应相等的两个三角形相似即可判定.
【详解】证明:∵,,
∴,,
∴.
【点睛】此题考查了相似三角形的判定,常用的判定方法有:
①有两个对应角相等的三角形相似;
②有两组对应边的比相等,且其夹角相等,则两个三角形相似;
③三组对应边的比相等,则两个三角形相似.
21.(1) 证明见解析;(2).
【详解】试题分析:
(1)由AB=AC,点D是BC的中点可得AD⊥BC,结合CD是⊙O的直径,即可得AD是⊙O的切线;
(2)连接OP,由已知易求得BD、OB、OP和BP的长,再证PE=DE,△BDE∽△BPO即可列出比例式求得DE的长,从而可得PE的长.
试题解析:
(1)∵AB=AC,点D是边BC的中点,
∴AD⊥CD,
∵CD为⊙O的直径,
∴AD是⊙O的切线;
(2)连接OP,
∵点D是边BC的中点,BC=4,CD是⊙O的直径,
∴CD=BD=2,OP=1,OB=3,
∴在Rt△BOP中,BP=,
∵AD是⊙O的切线,PB是⊙O的切线,
∴PE=DE,∠BPO=90°,
∵AD⊥CD,
∴∠ADB=∠BPO=90°,
又∵∠DBE=∠PBO,
∴△BDE∽△BPO,
∴,即,解得:DE=,
∴PE=DE=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
