第七章平行线的证明同步练习（含解析）

中小学教育资源及组卷应用平台
第七章平行线的证明
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．如果两条平行线被第三条直线所截，那么其中一组同位角的角平分线( )．
A．垂直 B．相交 C．平行 D．不能确定
2．如图，已知直线，，且，则等于（ ）
A． B．
C． D．
3．若要说明命题：“如果a＜b，那么a2＜b2”是假命题，则可以举的反例是（　　）
A．a＝2，b＝3 B．a＝﹣2，b＝﹣3 C．a＝﹣3，b＝﹣2 D．a＝﹣2，b＝3
4．试说明“若，，，则”是真命题．以下是排乱的推理过程：
①因为（已知）；
②因为，（已知）；
③所以，（等式的性质）；
④所以（等量代换）；
⑤所以（等量代换）．
正确的顺序是( )
A．①→③→②→⑤→④ B．②→③→⑤→①→④
C．②→③→①→⑤→④ D．②→⑤→①→③→④
5．在平面内，下列说法错误的是（ ）
A．过直线外一点有且仅有一条直线与已知直线平行
B．若一条直线上有两点到另一条直线距离相等，则这两条直线平行
C．同平行于一条直线的两条直线平行
D．同垂直于一条直线的两条直线平行
6．如图所示，两条直线被第三条直线所截，，下列说法正确的（　　）

A．若，则
B．若，则
C．若，则
D．若，则
7．如图，下列能判定的条件有（ ）
①；②；③；④；⑤.
A．2个 B．3个 C．4个 D．5个
8．下列说法不正确的是（　　）
A．证实命题正确与否的推理过程叫做证明
B．定理是命题，而且是真命题
C．“对顶角相等”是命题，但不是定理
D．要证明一个命题是假命题只要举出一个反例即可
9．已知，在中，，，则的度数为（ ）
A． B． C． D．
10．以下命题是假命题的是（ ）
A．平行于同一条直线的两条直线互相平行
B．内错角的平分线互相平行
C．两条边互相平行的两个角相等或互补
D．两条平行线被第三条直线所截，同位角的平分线互相平行
11．下列命题中，是真命题的是（ ）
A．同角的余角互补 B．同位角相等
C．两直线平行，内错角相等 D．三角形的一个外角大于任何一个内角
12．在中，、的平分线交于点O，的平分线所在直线与的平分线相交于点D，与的平分线相交于点E，则下列结论一定正确的是（ ）
①；②；③；④．
A．①②④ B．①②③ C．①② D．①②③④
二、填空题
13．如图，已知AB∥CD，∠DEF=50°，∠D=80°，∠B的度数是 .
14．如图所示，在中，，、分别平分，，则等于 ．
15．如图，将一个长方形纸条折成如图所示的形状，若已知，则 °．

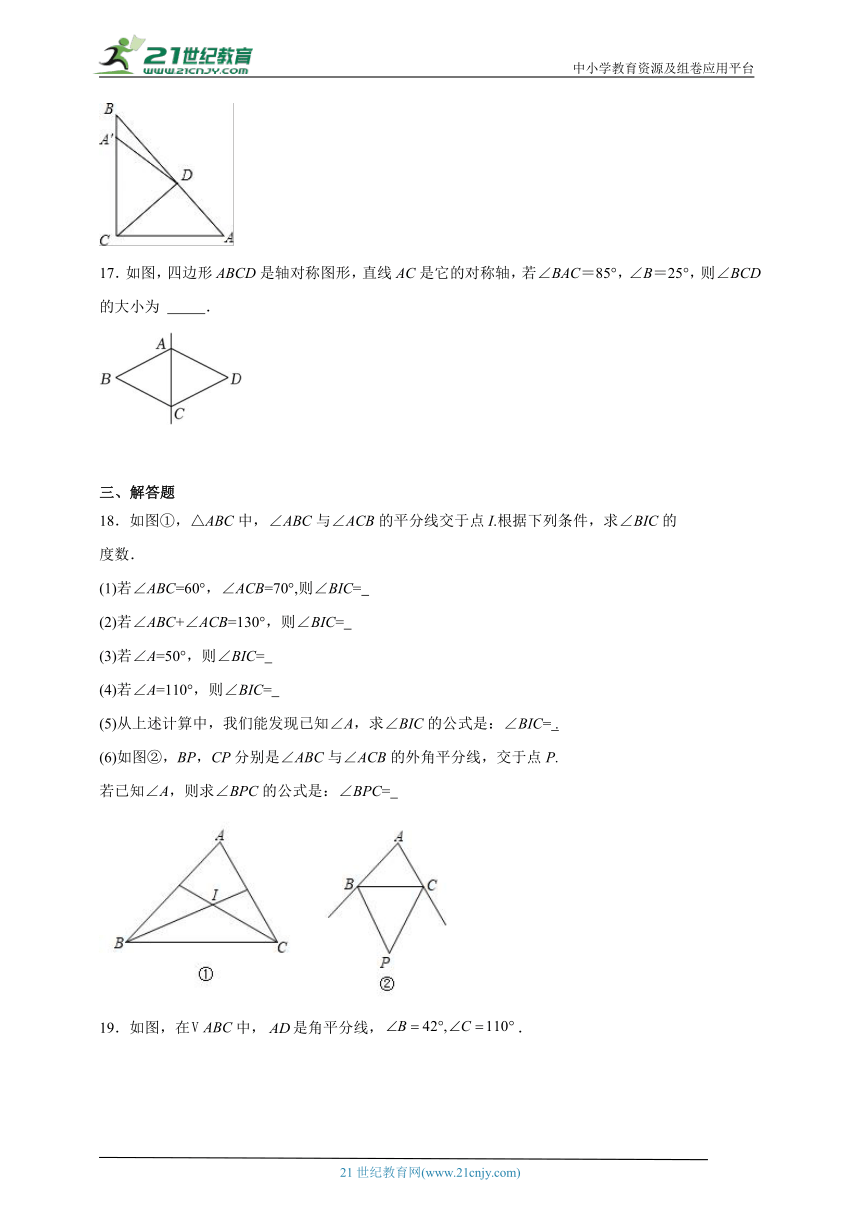
16．如图，在△ABC中，∠ACB=90°，∠A=50°．将△ACD沿CD翻折，点A恰好落在BC边上的A′处，则∠A′DB= ．
17．如图，四边形ABCD是轴对称图形，直线AC是它的对称轴，若∠BAC＝85°，∠B＝25°，则∠BCD的大小为 ．
三、解答题
18．如图①，△ABC中，∠ABC与∠ACB的平分线交于点I.根据下列条件，求∠BIC的
度数．
(1)若∠ABC=60°，∠ACB=70°,则∠BIC=
(2)若∠ABC+∠ACB=130°，则∠BIC=
(3)若∠A=50°，则∠BIC=
(4)若∠A=110°，则∠BIC=
(5)从上述计算中，我们能发现已知∠A，求∠BIC的公式是：∠BIC= .
(6)如图②，BP，CP分别是∠ABC与∠ACB的外角平分线，交于点P.
若已知∠A，则求∠BPC的公式是：∠BPC=
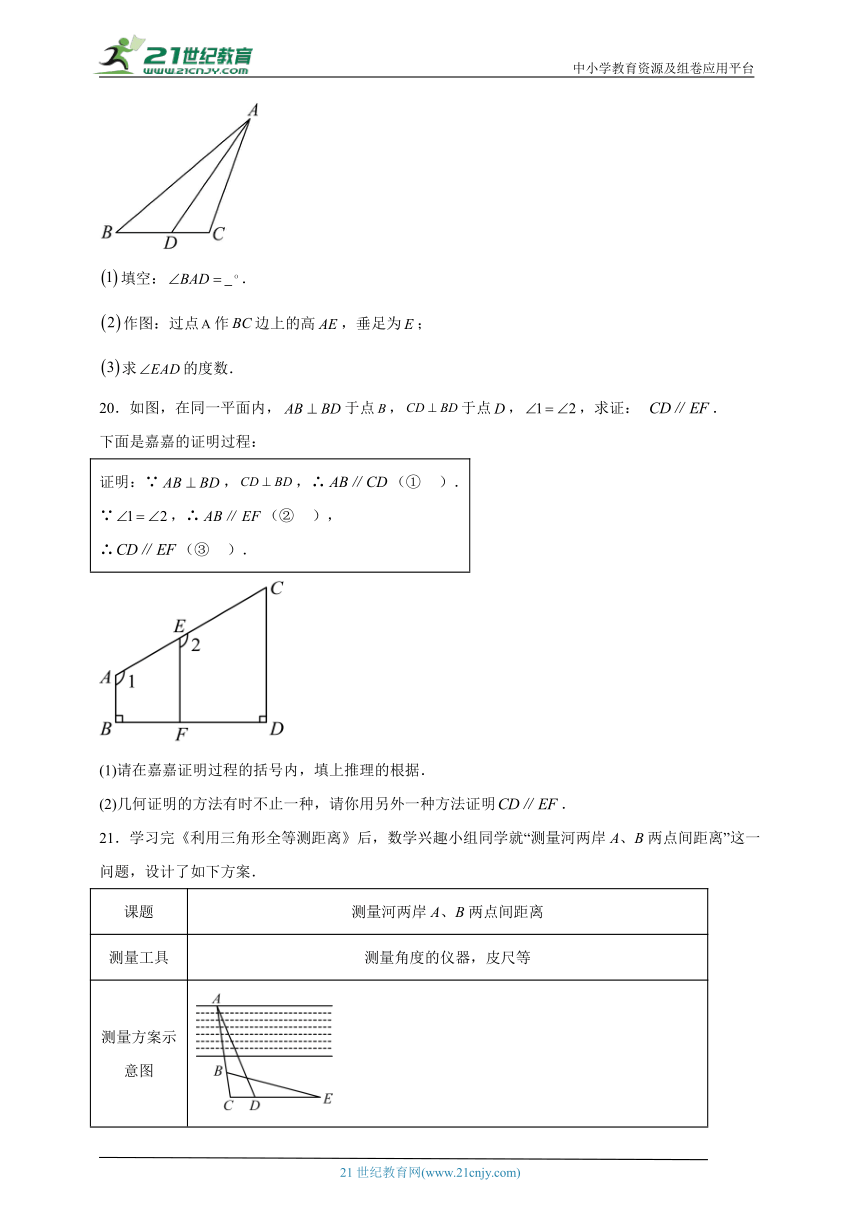
19．如图，在中，是角平分线，．

填空： ．
作图：过点作边上的高，垂足为；
求的度数．
20．如图，在同一平面内，于点，于点，，求证： ．
下面是嘉嘉的证明过程：
证明：∵，，∴（① ）． ∵，∴（② ）， ∴（③ ）．
(1)请在嘉嘉证明过程的括号内，填上推理的根据．
(2)几何证明的方法有时不止一种，请你用另外一种方法证明．
21．学习完《利用三角形全等测距离》后，数学兴趣小组同学就“测量河两岸A、B两点间距离”这一问题，设计了如下方案．
课题 测量河两岸A、B两点间距离
测量工具 测量角度的仪器，皮尺等
测量方案示意图
测量步骤 ①在点所在河岸同侧的平地上取点和点，使得点、、在一条直线上，且； ②测得； ③在的延长线上取点E，使得； ④测得的长度为30米．
请你根据以上方案求出、两点间的距离．
22．阅读下列材料，解决相应问题．
【学科融合】如图1，物理学光的反射现象中，把经过入射点并垂直于反射面的直线叫做法线，入射光线与法线的夹角叫做入射角，反射光线与法线的夹角叫做反射角，反射角入射角，这就是光的反射定律．
（1）在图1中，证明；
【问题解决】根据光的反射定律，人们制造了潜望镜，如图2是潜望镜的工作原理示意图，、是平行放置的两面平面镜，是射入潜望镜的光线，是经平面镜两次反射后离开潜望镜的光线，由（1）可知，光线经过平面镜反射时，有，；
（2）请问和有什么关系？并说明理由；
（3）请问光线和是否平行？并说明理由．
23．用两种方法证明“三角形的外角和等于”．
【提示】我们知道：三角形的内角和等于；三角形的外角等于不相邻的两个内角的和．
已知：如图，是的三个外角．
求证：．
证法1：是的一个外角，
①_______．
同理，．
．
．
②________
．
请把证法1补充完整，并用不同的方法完成证法2．
24．小明在学习过程中，对教材中的一个有趣问题做如下探究：

(1)（习题回顾）已知：如图1，在中，，是角平分线，是高，、相交于点F．求证：；
(2)（变式思考）如图2，在中，，是边上的高，若的外角的平分线交的延长线于点F，其反向延长线与边的延长线交于点E，则与还相等吗？说明理由；
(3)（探究延伸）如图3，在中，在上存在一点D，使得，角平分线交于点F．的外角的平分线所在直线与的延长线交于点M．试判断与的数量关系，并说明理由．
参考答案：
题号 1 2 3 4 5 6 7 8 9 10
答案 C C C C D B B C C B
题号 11 12
答案 C C
1．C
【分析】由两条平行线被第三条直线所截，根据两直线平行，同位角相等，即可得一组同位角相等即∠FEB=∠GFD，又由角平分线的性质求得∠1=∠2，然后根据同位角相等，两直线平行，即可求得答案．
【详解】解：如图，
∵AB∥CD，

∴∠FEB=∠GFD，
∵EM与FN分别是∠FEB与∠GFD的平分线，
∴∠1=∠FEB，∠2=∠GFD，
∴∠1=∠2，
∴EM∥FN．
故选C．
【点睛】本题考查了平行线性质的应用，注意：平行线的性质有：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，题目比较好，难度适中．
2．C
【分析】根据两直线平行，同旁内角互补得出∠CFB，根据AE＝AF可得出∠E＝∠EFA，根据三角形的内角和为180°可求∠A．
【详解】解：∵AB∥CD，∠DCF＝115°，
∴∠CFB＝180° 115°＝65°，
∴∠AFE＝∠CFB＝65°，
∵AE＝AF，
∴∠E＝∠AFE＝65°，
在△AEF中，∠A＝180° 65° 65°＝50°．
故选C．
【点睛】本题主要利用平行线的性质和三角形内角和定理求解，是基础题，要熟练掌握．
3．C
【分析】逐项进行计算，然后进行判断即可．
【详解】解：A. a＝2，b＝3，有a＜b， a2＜b2，不符合题意；
B. a＝﹣2，b＝﹣3，有a＞b，不符合题意；
C. a＝﹣3，b＝﹣2，有a＜b， a2＞b2，符合题意；
D. a＝﹣2，b＝3有a＜b， a2＜b2，不符合题意；
故选：C．
【点睛】本题考查了有理数的运算和假命题的判断，解题关键是熟练进行计算，准确进行判断．
4．C
【分析】写出正确的推理过程，进行排序即可．
【详解】证明：因为，（已知），
所以，（等式的性质）；
因为（已知），
所以（等量代换）．
所以（等量代换）．
∴排序顺序为：②→③→①→⑤→④．
故选C．
【点睛】本题考查推理过程．熟练掌握推理过程，是解题的关键．
5．D
【分析】此题考查了平行线的判定和性质，平行公理及推论，根据平行线的判定和性质，平行公理及推论进行判断即可．
【详解】解：A．过直线外一点有且仅有一条直线与已知直线平行，故选项正确，不符合题意；
B．若一条直线上有两点到另一条直线距离相等，则这两条直线平行，故选项正确，不符合题意；
C．同平行于一条直线的两条直线平行，故选项正确，不符合题意；
D．在同一平面内，同垂直于一条直线的两条直线平行，故选项错误，符合题意．
故选：D．
6．B
【分析】根据对顶角相等、邻补角互补，以及同位角相等两直线平行，逐一判定即可．
【详解】解：A、∵，∴，而，∴不能判定，本选项不符合题意；
B、∵，∴，而，∴，本选项符合题意；
C、若，属于对顶角相等，不能判定，本选项不符合题意；
D、若，属于邻补角互补，不能判定，本选项不符合题意；
故选：B．
【点睛】本题主要考查两直线平行的判定定理，熟记概念是解题关键．
7．B
【分析】本题主要考查平行线的判定，熟练掌握平行线的判定是解题的关键；因此此题可根据平行线的判定定理进行求解．
【详解】解：①由可知；②由可知；③由可知；④由可知；⑤由可知；所以符合判定的条件有3个；
故选：B．
8．C
【分析】本题考查了定理于命题的相关知识点，掌握命题，定理和证明的概念是关键.
【详解】解：证实命题正确与否的推理过程叫做证明，故A正确，不符合题意；
定理是命题，而且是真命题，故B正确，不符合题意；
对顶角相等”是命题，此命题是通过推理证实得出的真命题，所以它是定理，故C错误，符合题意；
要证明一个命题是假命题只要举出一个反例即可，故D正确，不符合题意；
故选：C
9．C
【分析】根据题意与三角形的内角和即可求解.
【详解】∵，
∴，
又∠A+∠B+∠C=180°，
则=180°，
解得∠B=，故选C.
【点睛】此题主要考查三角形的内角和的应用，解题的关键是熟知三角形的内角和为180°.
10．B
【分析】本题考查了真假命题的判断，熟练掌握平行线的性质与判定是解题的关键．
根据平行线的判定和性质，逐项判断即可．
【详解】A．根据平行公理知：平行于同一条直线的两条直线互相平行，是真命题，故选项不符合题意；
B．当两条直线不是平行线时，内错角的平分线就不相等，是假命题，故选项符合题意；
C． 如图
，
，，
；
，
，，
，是真命题，故选项不符合题意；
D．如图
，
，
平分，
，
，
两条平行线被第三条直线所截，同位角的平分线互相平行是真命题，故选项不符合题意；
故选：B．
11．C
【分析】本题主要考查真假命题，余角，同位角，平行线的性质，三角形外角等知识，根据其概念和性质进行判断即可，熟练掌握相应的知识是解题的关键．
【详解】A. 同角的余角相等，不符合题意；
B. 同位角不一定相等，不符合题意；
C. 两直线平行，内错角相等，符合题意；
D. 三角形的一个外角大于任何一个不相邻的内角，不符合题意；
故选：C．
12．C
【分析】本题主要考查三角形的内角和定理，角平分线的定义，三角形外角的性质，熟练掌握角平分线的定义和三角形的外角性质，并能进行推理计算是解决问题的关键．由角平分线的定义可得，再由三角形的内角和定理可求解，即可判定①；由角平分线的定义可得，结合三角形外角的额性质可判定②；由三角形外角的性质可得，再利用角平分线的定义及三角形的内角和定理可判定③；利用三角形外角的性质可得，结合可判定④．
【详解】解：∵，的平分线交于点O，
∴，，
∴
，
∴
，故①正确，
∵平分，
∴，
∵，，
∴，
∴，故②正确；
∵，，，
∴，
∵平分，平分，
∴，，
∴，
∴，故③错误；
∵，
∴，
∵，
∴，故④错误；
综上分析可知，正确的有：①②．
故选：C．
13．50°
【详解】试题解析：∵∠DEF=50°，∠D=80°，
∴∠DFE=50°，
又∵AB∥CD，
∴∠B=∠DFE=50°．
点睛：两条平行线被第三条直线所截，内错角相等． 简单说成：两直线平行，内错角相等．
14．/110度
【分析】首先根据三角形内角和定理得到，然后根据角平分线的性质得到，最后根据三角形内角和定理即可求出的度数．
【详解】解：∵在中，，
∴，
∵、分别平分，，
∴，
∴．
故答案为：．
【点睛】本题主要考查了三角形的内角和定理以及角平分线的定义，要熟练掌握，解答此题的关键是要明确：三角形的内角和是180°．
15．
【分析】由折叠可得，再利用平行线性质即可求解．
【详解】解：如图所示：

由题意可得：
，
图形为长方形，
，
，
，
故答案为：．
【点睛】本题考查了矩形的折叠问题及平行线的性质，熟练掌握平行线的性质是解题的关键．
16．10°.
【详解】试题分析：根据翻折变换的性质得出∠ACD=∠BCD=45°，∠CDA=∠CDA′=85°，进而利用三角形内角和定理得出∠ADC=∠A′DC=85°，再利用平角的定义，即可得∠BDA'=180°﹣85°﹣85°=10°．
故答案为10°．
考点：三角形内角和定理；翻折变换（折叠问题）．
17．140°/140度
【分析】根据轴对称的性质有 ,用三角形内角和定理求出 ，即可求出BCD．
【详解】由四边形ABCD是轴对称图形，有
故答案为
【点睛】本题考查了轴对称图形的性质与三角形内角和定理的性质与应用，知道轴对称进而判断出是关键．
18．(1)115°
(2)115°
(3)115°
(4)145°
(5)90°+∠A
(6)90°∠A
【分析】（1）根据角平分线的定义和三角形的内角和定理求解即可；
（2）根据角平分线的定义和三角形的内角和定理求解即可；
（3）先根据三角形内角和定理求得∠ABC+∠ACB=130°，然后再根据角平分线的定义和三角形的内角和定理求解即可；
（4））先根据三角形内角和定理求得∠ABC+∠ACB=130°，然后再根据角平分线的定义和三角形的内角和定理求解即可；
（5）先根据三角形内角和定理可得∠ABC+∠ACB=180°﹣∠A=130°，再根据角平分线的定义可得∠CBI+∠BCI=（∠ABC+∠ACB）=×130°=65°，最后根据三角形内角和定理即可解答；
（6）由三角形外角的性质可得∠CBD=∠A+∠ACB，∠BCE=∠A+∠ABC，进而得到∠CBD+∠BCE=∠A+∠ACB+∠A+∠ABC=180°+∠A，然后再根据角平分线的定义可得∠CBP+∠BCP=（∠CBD+∠BCE）=（180°+∠A）=90°+∠A，最后再根据三角形内角和定理即可解答．
【详解】（1）解：∵BI是∠ABC的平分线，∠ABC=60°，
∴∠CBI=∠ABC=30°．
∵CI是∠ACB的平分线，∠ACB=70°，
∴∠BCI=∠ACB=35°．
∵在△BCI中，∠BIC+∠BCI+∠CBI=180°，
∴∠BIC=180°﹣30°﹣35°=115°．
（2）解：∵BI是∠ABC的平分线，CI是∠ACB的平分线，
∴∠CBI=∠ABC，∠BCI=∠ACB，
∴∠CBI+∠BCI=（∠ABC+∠ACB）=×130°=65°．
∵在△BCI中，∠BIC+∠BCI+∠CBI=180°，
∴∠BIC=180°﹣65°=115°．
（3）解：∵在△ABC中，∠A+∠ABC+∠ACB=180°，∠A=50°，
∴∠ABC+∠ACB=180°﹣∠A=130°．
∵BI是∠ABC的平分线，CI是∠ACB的平分线，
∴∠CBI=∠ABC，∠BCI=∠ACB，
∴∠CBI+∠BCI=（∠ABC+∠ACB）=×130°=65°．
∵在△BCI中，∠BIC+∠BCI+∠CBI=180°，
∴∠BIC=180°﹣65°=115°．
（4）解：∵在△ABC中，∠A+∠ABC+∠ACB=180°，∠A=110°，
∴∠ABC+∠ACB=180°﹣∠A=70°．
∵BI是∠ABC的平分线，CI是∠ACB的平分线，
∴∠CBI=∠ABC，∠BCI=∠ACB，
∴∠CBI+∠BCI=（∠ABC+∠ACB）=×70°=35°．
∵在△BCI中，∠BIC+∠BCI+∠CBI=180°，
∴∠BIC=180°﹣35°=145°．
（5）解：∵在△ABC中，∠A+∠ABC+∠ACB=180°，
∴∠ABC+∠ACB=180°﹣∠A．
∵BI是∠ABC的平分线，CI是∠ACB的平分线，
∴∠CBI=∠ABC，∠BCI=∠ACB，
∴∠CBI+∠BCI=（∠ABC+∠ACB）=×（180°﹣∠A）=90°﹣∠A．
∵在△BCI中，∠BIC+∠BCI+∠CBI=180°，
∴∠BIC=180°﹣（90°﹣∠A）=90°+∠A．
（6）解：∵∠CBD，∠BCE是△ABC的外角，
∴∠CBD=∠A+∠ACB，∠BCE=∠A+∠ABC，
∴∠CBD+∠BCE=∠A+∠ACB+∠A+∠ABC=180°+∠A．
∵BP，CP分别是∠ABC与∠ACB的外角平分线，
∴∠CBP=∠CBD，∠BCP=∠BCE
∴∠CBP+∠BCP=（∠CBD+∠BCE）=（180°+∠A）=90°+∠A．
∵在△BCP中，∠BCP+∠CBP+∠BPC=180，
∴∠BPC=180°﹣（90°+∠A）=90°﹣∠A．
【点睛】本题主要考查了三角形的内角和定理、角平分线、三角形外角的性质等知识点，灵活运用三角形角平分线的定义成为解答本题的关键．
19．（1）14；（2）见解析；（3）39°
【分析】（1）求出∠BAC，再利用角平分线的定义求解即可．
（2）根据高的定义画出图形即可．
（3）利用三角形的外角的性质求出∠ADE即可解决问题．
【详解】解：∵∠B＝42°，∠C＝110°，
∴∠ABC＝180° 42° 110°＝28°，
∵AD是角平分线，
∴∠BAD＝∠BAC＝14°．
故答案为14．
线段即为所求作的高．

由知
是高
答：的度数为．
【点睛】本题考查作图 基本作图，三角形内角和定理等知识，解题的关键是熟练掌握五种基本作图，属于中考常考题型．
20．(1)见解析
(2)见解析
【分析】此题考查了平行线的判定，利用同位角相等证明两直线平行是解答此题的关键．
（1）根据，，得出，再根据，得出，即可证出；
（2）证明，再根据同旁内角互补，两直线平行即可．
【详解】（1）解：（1）①在同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线平行．
②同位角相等，两直线平行．
③如果两条直线都与第三条直线平行，那么这两条直线也互相平行．
（2）证明：∵，，
∴，
∴．
∵，
∴，
∴．
21．、两点间的距离为30米
【分析】本题考查了三角形内角和定理，全等三角形的判定和性质，熟练掌握全等三角形的性质是解题关键．由三角形内角和定理，得出，进而证明，推出，即可求解．
【详解】解：，
．
，
．
在和中，
，
．
，
，
米，
即、两点间的距离为30米．
22．（1）见解析；（2），理由见解析；（3）理由见解析．
【分析】本题考查了平行线的性质和判定的应用，能灵活运用定理进行推理是解此题的关键．
（1）根据等角的余角相等解答即可；
（2）根据平行线的性质求解即可；
（3）求出，根据平行线的判定得出即可．
【详解】（1）∵，，
∴；
（2）∵，
∴；
（3）由材料可知，，
∴，
∴，
∴，
∴．
23．① ∠BAE=∠2+∠3，② ∠1+∠2+∠3=180°；
证法2见详解
【分析】证法1：根据是的一个外角，可得．同理可得．．即有，再结合即可求证；证法2，根据平角为180°可得，，，即有，再结合即可求证．
【详解】证法1：∵是的一个外角，
∴．
同理，．
．
∴．
∵，
∴．
故答案为：①，②；
证法2：
∵，，，
∴，
∵，
∴．
【点睛】本题考查了三角形的内角和等于180°和三角形的外角等于不相邻的两个内角的和的知识，掌握三角形的外角等于不相邻的两个内角的和的知识是解答本题的关键．
24．(1)见解析
(2)相等，理由见解析
(3)，理由见解析
【分析】习题回顾：先证明，，再利用三角形的外角的性质可得：，，从而可得结论；
变式思考： 先证明， ，结合， 可得；
探究延伸： 先证明，， 可得， 结合，，，， 可得， 从而可得答案．
【详解】（1）习题回顾：证明：∵，是高，
∴，，
∴，
∵是角平分线，
∴，
∵，，
∴；
（2）变式思考：，
证明：∵为的角平分线，
∴，
∵为边上的高，
∴，
∴，
又∵，
∴；
（3）探究延伸：，
证明：∵C、A、G三点共线 、为角平分线，
∴，
又∵，
∴，
∴，
∵，，，，
∴，
∴．
【点睛】本题考查的是三角形的外角的性质、三角形内角和定理，掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)