5.7用二元一次方程组确定一次函数表达式同步练习(含解析)
文档属性
| 名称 | 5.7用二元一次方程组确定一次函数表达式同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 924.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-15 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
5.7用二元一次方程组确定一次函数表达式
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知y是x的一次函数,下表列出了部分y与x的对应值:
x 0 1 2
y 0 2 a
则a的值为( )
A. B.1 C.3 D.4
2.小明根据某个一次函数关系式填写了如下的表格:其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是( )
-2 0 1
6 2 0
A.-2 B.0 C.2 D.4
3.在一条笔直的公路上A、B两地相120km,甲车从A地开往B地,乙车从B地开往A地,甲比乙先出发.设甲、乙两车距A地的路程为y千米,甲车行驶的时间为x小时,y与x之间的关系如图所示,下列说法错误的是( )
A.甲车的速度比乙的速度慢 B.甲车出发1小时后乙才出发
C.甲车行驶了2.8h或3.2h时,甲、乙两车相距10km D.乙车达到A地时,甲车离A地90km
4.过点(0,0)的直线是( ).
A.y=x-1 B.y=x+2 C.y=-2x D.y=-2x+1
5.已知直线经过点(k,3)和(1,k),则k的值为( )
A. B. C. D.
6.若三点在同一条直线上,则a的值为( )
A.4 B.2 C. D.
7.过原点和点(2,3)的直线的解析式为( )
A.y=x B.y=x C.y=x+1 D.y=-2x+7
8.已知点,,点,过点作轴的平行线交直线于点,则线段的长为( )
A. B. C. D.
9.如图,一次函数的图象分别与轴、轴交于点、,以线段为边在第一象限内作等腰,,则过、两点直线的解析式为( )
A. B. C. D.
10.如图,的顶点,,点C在y轴的正半轴上,,将向左平移得到.若经过点,则点的坐标为( ).
A. B. C. D.
11.已知正比例函数(,为常数),经过点(3,6),以下哪个点不在该正比例函数图象上( )
A.(-3,-6) B.(0,0) C.(1,2) D.(-1,2)
12.在平面直角坐标系中,已知点,点,在x轴上确定点C,使得的周长最小,则点C的坐标是( )
A. B. C. D.
二、填空题
13.已知一次函数图象经过与两点,则该函数的图象与y轴交点的坐标为 .
14.一次函数y=kx+b,当3≤x≤4时,3≤y≤6,则的值是 .
15.已知y与成正比例,且当时,,那么当时,y的值为 .
16.直线与平行,且经过,则 .
17.已知经过点(1,-2)的直线是由向下平移后得到的,那么这条直线的解析式是 .
三、解答题
18.已知y是x的一次函数,且当时,;当时,.
(1)求这个一次函数的表达式;
(2)通过计算,判断点是否在这个函数的图象上?
19.一列火车以的速度匀速前进.求它的行驶路程s(单位:)关于行驶时间t(单位:h)的函数解析式,并画出函数图象.
20.下图是某市轻轨列车两站之间行驶速度v(米/秒)与行驶时间t(秒)之间的函数图象,已知点,点,点.
(1)求线段的函数解析式.
(2)求这两站之间列车速度不低于30米/秒的行驶时间.
21.我们知道,弹簧的总长度是所挂重物的一次函数,请根据如图所示的信息解决问题.
(1)求一次函数表达式;
(2)求弹簧不挂重物时的长度.
22.综合与实践
某班同学分三个小组进行“板凳中的数学”的项目式学习研究,第一小组负责调查板凳的历史及结构特点;第二小组负责研究板凳中蕴含的数学知识:第三小组负责汇报和交流,下面是第三小组汇报的部分内容,请你阅读相关信息,并解答“建立模型”中的问题.
【背景调查】
图①中的板凳又叫“四脚八叉凳”,是中国传统家具,其榫卯结构体现了古人含蓄内敛的审美观.榫眼的设计很有讲究,木工一般用铅笔画出凳面的对称轴,以对称轴为基准向两边各取相同的长度,确定榫眼的位置,如图②所示.板凳的结构设计体现了数学的对称美.
【收集数据】
小组收集了一些板凳并进行了测量.设以对称轴为基准向两边各取相同的长度为,凳面的宽度为,记录如下:
以对称轴为基准向两边各取相同的长度 16.5 19.8 23.1 26.4 29.7
凳面的宽度 115.5 132 148.5 165 181.5
【分析数据】
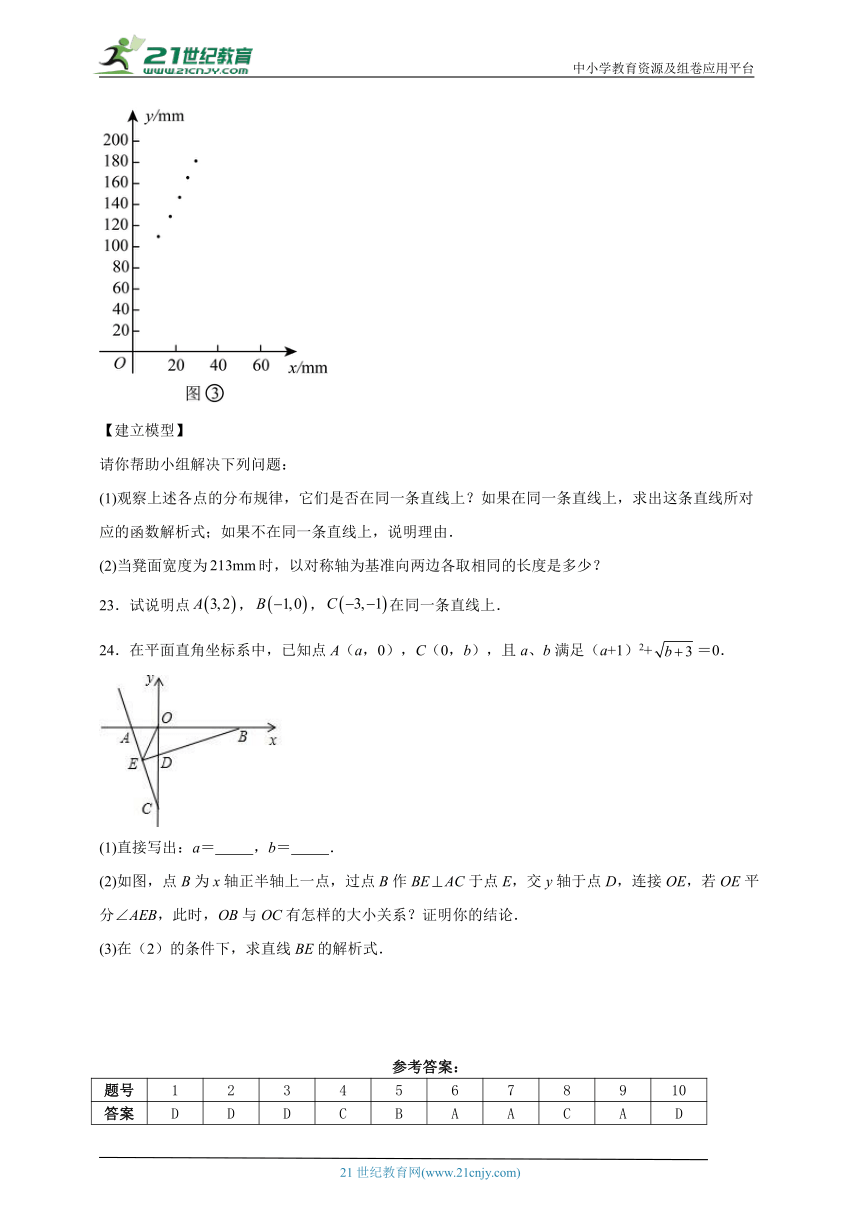
如图③,小组根据表中x,y的数值,在平面直角坐标系中描出了各点.
【建立模型】
请你帮助小组解决下列问题:
(1)观察上述各点的分布规律,它们是否在同一条直线上?如果在同一条直线上,求出这条直线所对应的函数解析式;如果不在同一条直线上,说明理由.
(2)当凳面宽度为时,以对称轴为基准向两边各取相同的长度是多少?
23.试说明点,,在同一条直线上.
24.在平面直角坐标系中,已知点A(a,0),C(0,b),且a、b满足(a+1)2+=0.
(1)直接写出:a= ,b= .
(2)如图,点B为x轴正半轴上一点,过点B作BEAC于点E,交y轴于点D,连接OE,若OE平分∠AEB,此时,OB与OC有怎样的大小关系?证明你的结论.
(3)在(2)的条件下,求直线BE的解析式.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D D D C B A A C A D
题号 11 12
答案 D C
1.D
【分析】设出一次函数的解析式,采用待定系数法,在表格中选择两个点的坐标代入解析式中,求出解析式,然后再将x=2代入解析式中求出a的值即可.
【详解】解:由题意知,设一次函数的解析式为:
代入点
即,解得
故一次函数的解析式为:
将x=2,y=a时,代入解析式中,解得a=4.
故答案为:D.
【点睛】本题考查用待定系数法求一次函数的解析式,将点的坐标代入解析式中,联立二元一次方程组即可求解.
2.D
【分析】首先根据待定系数法求出一次函数的解析式,然后把x= 1代入,即可求出对应的y值.
【详解】解:设一次函数的解析式为y=kx+b.
把x=0,y=2;x=1,y=0代入,
得,
解得,
∴.
当x= 1时,y=4.
故选D
【点睛】本题考查了待定系数法求一次函数解析式,掌握待定系数法求一次函数解析式是解题的关键.
3.D
【分析】根据图象直接判断A;求出两车的路程y与时间x之间的函数关系式,即可判断B、C、D
【详解】解:当甲出发时乙未出发,甲行驶5小时未到达B地,而乙已经到达A地,说明甲车的速度比乙的速度慢,故选项A正确;
设甲车的路程y与时间x之间的函数关系式为,代入,
得,
解得,
∴甲车的路程y与时间x之间的函数关系式为;
设乙车的路程y与时间x之间的函数关系式为,代入和,
,解得,
∴乙车的路程y与时间x之间的函数关系式为,
当时,,解得,
即甲车出发1小时后乙才出发,故选项B正确;
当时,解得;
当时,解得;
∴甲车行驶了2.8h或3.2h时,甲、乙两车相距10km,故选项C正确;
当时,,故选项D错误;
故选:D.
【点睛】此题考查了一次函数的图象,求一次函数的解析式,一次函数的应用,正确理解一次函数的图象得到相关信息是解题的关键.
4.C
【详解】试题分析:由一次函数的图象和性质可知,图象过原点(0,0),那么一定是正比例函数,在这四个选项中,只有C是正比例函数.
故选C.
考点:一次函数的图象和性质.
5.B
【分析】运用待定系数法求一次函数解析式,代入后求出k,b的值即可.
【详解】∵直线y=kx+b经过点(k,3)和(1,k),
∴将(k,3)和(1,k),代入解析式y=kx+b得:
解得:k=±,b=0,
则k的值为:±.
故选B.
6.A
【分析】设这条直线解析式为,先把B点和C点坐标代入,待定系数法求解析式得出,当时,求得的值,即可求解.
【详解】解:设这条直线解析式为,,
,
解得:,
∴直线解析式为,
将点代入得,,
解得,
故选:A.
【点睛】本题考查了待定系数法求一次函数解析式,求得一次函数解析式是解题的关键.
7.A
【分析】采用待定系数法求解析即可.
【详解】设直线解析式为:
将(0,0),(2,3)代入解析式得:
,解得,
所以直线解析式为:,
故选A.
【点睛】本题考查求函数解析式,熟练掌握待定系数法是关键.
8.C
【分析】先利用待定系数法求出直线AB的解析式,再求出点D坐标,进而可求出CD的长.
【详解】解:设直线AB的解析式为y=kx+b,
将A(﹣1,0)、B(0,﹣3)代入,
得:,解得:,
∴直线AB的解析式为y=﹣3x﹣3,
∵点C(2,﹣2)且CD∥x轴交直线AB于点D,
∴当y=﹣2时,由﹣2=﹣3x﹣3得:x= ,
∴D(,﹣2),
∴CD=2﹣()= ,
故选:C.
【点睛】本题考查待定系数法求一次函数的解析式、坐标与图形,熟练掌握待定系数法求函数的解析式的方法,求出点D坐标是解答的关键.
9.A
【分析】易得OB=3,OA=4,由在等腰中,,得 AOB CDA(AAS),从而得C(7,4),进而根据待定系数法,即可得到答案.
【详解】∵一次函数的图象分别与轴、轴交于点、,
∴A(4,0),B(0,3),
∴OB=3,OA=4,
过点C做CD⊥x轴于点D,
∵在等腰中,,
∴∠OAB+∠CAD=∠OAB+∠ABO,即:∠CAD=∠ABO,
∵AB=AC,∠AOB=∠ADC=90°,
∴ AOB CDA(AAS),
∴CD=AO=4,AD=BO=3,
∴C(7,4),
设直线的解析式为:y=kx+b,
把B(0,3),C(7,4),代入y=kx+b,得,解得:,
∴直线的解析式为:y=x+3,
故选A.
【点睛】本题主要考查一次函数图象与全等三角形的判定与性质定理,掌握“一线三垂直”全等模型,是解题的关键.
10.D
【分析】设点C的坐标为,利用勾股定理分别求出的长,结合,即可求出点C的坐标,求出直线的解析式,即可求出直线的解析式,从而推出直线相当于直线向左平移3个单位得到的,由此即可得到答案.
【详解】解:设点C的坐标为,
则由勾股定理得:,,
∵,
∴,
∴或(舍去),
∴点C的坐标为,
设直线的解析式为,
∴,
∴,
∴直线的解析式为,
∵是经过平移得到的,
∴可设直线的解析式为,
∵经过点,
∴,
∴直线的解析式为,
∴直线相当于直线向左平移3个单位得到的,
∴点是由点C向左平移3个单位得到的,
∴点的坐标为,
故选:D.
【点睛】本题主要考查了一次函数的平移,勾股定理,待定系数法求一次函数解析式等等,熟知一次函数的相关知识是解题的关键.
11.D
【分析】先利用已知点求得正比例函数的解析式,然后每个选项中点代入验证即可.
【详解】解:∵正比例函数(,为常数),经过点(3,6),
∴,解得,
∴正比例函数的解析式为,
把(-3, 6)代入, 6=2×(-3),故选项A在这个函数图象上,
把(0,0)代入,0=2×0,故选项B在这个函数图象上;
把(1,2)代入,2=2×1,故选项C在这个函数图象上;
把(-1,2)代入,2≠2×(-1),故选项D在这个函数图象上;
故选:D
【点睛】此题主要考查了一次函数的性质,以及函数图象上点的坐标特点,待定系数法求一次函数解析式,关键是掌握凡是函数图象经过的点必能满足解析式.
12.C
【分析】因为AB的长度是确定的,故△CAB的周长最小就是CA+CB的值最小,作点A关于x轴的对称点A′,连接A′B交x轴于点C,求出C点坐标即可.
【详解】解:如图,作点A关于x轴的对称点A′,连接A′B交x轴于点C,此时,AC+BC=A′C+BC=AC,长度最小,
∵A(-1,2),
∴A′(-1,﹣2),
设直线A′B的解析式为y=kx+b(k≠0),把A′(-1,﹣2),代入得,
∴,解得,
∴直线A′B的解析式为y=-2x﹣4,
当y=0时,x=-2,
∴C(-2,0).
故选:C
【点睛】本题考查了轴对称-最短路径问题,一次函数与坐标轴交点问题,解题关键是确定点C的位置,利用一次函数解析式求坐标.
13.(0,)
【分析】设一次函数的解析式为y=kx+b,然后把与两点分别代入求出一次函数解析式,进而问题可求解.
【详解】设一次函数的解析式为y=kx+b,
把与两点分别代入得
,
解得:,
所以一次函数的解析式为:,
当x=0时,y=,
所以该函数的图象与y轴交点的坐标为(0,),
故答案为(0,).
【点睛】本题考查了一次函数图象与坐标轴的交点问题,熟练掌握待定系数法是解本题的关键.
14.-2或-5/-5或-2
【分析】由于k的符号不能确定,故应对k>0和k<0两种情况进行解答.
【详解】解:当k>0时,此函数是增函数,
∵当3≤x≤4时,3≤y≤6,
∴当x=3时,y=3;当x=4时,y=6,
∴,解得
∴= 2;
当k<0时,此函数是减函数,
∵当3≤x≤4时,3≤y≤6,
∴当x=3时,y=6;当x=4时,y=3,
∴,解得
∴=-5.
故答案为-2或-5.
【点睛】本题考查的是一次函数的性质,在解答此题时要注意分类讨论,不要漏解.
15.
【分析】
本题考查的是正比例函数,解答本题的关键是熟练掌握正比例函数的一般形式: .由题意设,根据当时,,即可求出k的值,从而得到结果.
【详解】
解:设,
把,,代入得:
,
解得,
∴,
当时,.
故答案为:
16.-3
【分析】根据直线与直线平行得到,把代入即可求出b,即可求解.
【详解】解:∵直线与直线平行
∴
把代入得:
∴
故答案为: .
【点睛】本题考查的是用待定系数法求一次函数的解析式,解答此题的关键是要熟知两直线平行时其未知数的系数相等.
17.y=3x-5
【分析】根据平移规律可知,k=3,则向下平移后得到的解析式为y=3x+b,将(1,-2)代入求解即可.
【详解】解:∵直线是由向下平移后得到的
∴k=3
∴y=3x+b
∵直线经过点(1,-2)
∴-2=3×1+b
∴b=-5
∴y=3x-5
故答案为:y=3x-5
【点睛】本题考查了求一次函数的解析式及平移规律,解题的关键是掌握一次函数平移的规律.
18.(1)y=3x-5;(2)点P(4,6)不在这个函数的图象上.
【分析】(1)设一次函数解析式为y=kx+b,然后用待定系数法求出k、b,即可得到答案;
(2)计算x为4时对应的一次函数值,然后根据一次函数图象上的点的坐标特征进行判断.
【详解】解:(1)设一次函数解析式为y=kx+b,
根据题意得 ,
解得,
∴这个一次函数的表达式为y=3x-5;
(2)∵当x=4时,
y=3x-5=3×4-5=7≠6,
∴点P(4,6)不在这个函数的图象上.
【点睛】本题考查了待定系数法求一次函数解析式,一次函数图象上点的坐标特征,熟练掌握待定系数法是解题的关键.
19..图象见解析
【分析】根据公式路程=速度×时间先列出函数解析式,然后画出函数图象即可.
【详解】解:∵火车以的速度匀速前进,
∴它的行驶路程s(单位:)关于行驶时间t(单位:h)的函数解析式为:.
当时,,
当时,.
作图如下:
【点睛】本题考查列函数解析式,以及画函数图象,掌握画函数图象的方法是解题关键.
20.(1)
(2)秒
【分析】本题主要考查一次函数的应用,熟悉相关的知识是解题的关键;(1)根据待定系数法把点B、点C待入解析式即可求解;(2)求出的解析式,把30代入即可求解.
【详解】(1)解:设线段的解析式为:;
把,代入解析式得:
;
解得:;
∴
(2)设线段的解析式为:;
把代入,得;
∴;
把代入得;
把代入得;
∴列车速度不低于30米/秒的行驶时间为:(秒).
21.(1)
(2)弹簧不挂重物时的长度为
【分析】本题考查了运用待定系数法求一次函数的解析式的运用,由自变量求函数值的运用,解答时求出函数的解析式是关键.
(1)设与的函数关系式为,由待定系数法求出其解即可;
(2)把时代入解析式求出的值即可.
【详解】(1)设,
由图可知:图像经过,
,
解得,
∴一次函数表达式为:;
(2)由题意得,当时,.
答:弹簧不挂重物时的长度为.
22.(1)在同一条直线上,函数解析式为:
(2)
【分析】本题考查了一次函数的实际应用,待定系数法求函数解析式,已知函数值求自变量,熟练掌握知识点,正确理解题意是解题的关键.
(1)用待定系数法求解即可;
(2)将代入函数解析式,解方程即可.
【详解】(1),
解:设函数解析式为:,
∵当,,
∴,
解得:,
∴函数解析式为:,
经检验其余点均在直线上,
∴函数解析式为,这些点在同一条直线上;
(2)解:把代入得:
,
解得:,
∴当凳面宽度为时,以对称轴为基准向两边各取相同的长度为.
23.见解析
【分析】本题主要考查了一次函数的性质,求一次函数解析式,用待定系数法先求出过任意两点的一次函数解析式,再把另外一个点代入,如果成立,就三点共线.
【详解】证明:设经过点,的函数解析式为,则:
,
解得:,
∴直线的解析式为:,
把代入得:,
∴在直线上,
∴三点在同一条直线上.
24.(1)﹣1,﹣3
(2)OB=OC,证明见解析
(3)
【分析】(1)利用非负数的性质可求得a、b的值;
(2)过O作OF⊥OE,可得△OEF为等腰直角三角形,可证明△EOC≌△FOB,可证明OB=OC;
(3)可证明△AOC≌△DOB,可求得D点坐标,由(2)可求得B点坐标,从而可求得直线BE的解析.
【详解】(1)解:∵(a+1)2+=0,
∴a+1=0,b+3=0,
∴a=-1,b=-3,
故答案为:-1;-3;
(2)解:OB=OC,证明如下:
如图,过O作OF⊥OE,交BE于F,
∵BE⊥AC,OE平分∠AEB,
∴△EOF为等腰直角三角形,
∴∠EOC+∠DOF=∠DOF+∠FOB=90°,
∴∠EOC=∠FOB,且∠OEC=∠OFB=135°,
在△EOC和△FOB中,,
∴△EOC≌△FOB(ASA),
∴OB=OC;
(3)解:∵△EOC≌△FOB,
∴∠OCE=∠OBE,OB=OC,
在△AOC和△DOB中,
,
∴△AOC≌△DOB(ASA),
∴OD=OA,
∵A(-1,0),C(0,-3),
∴OD=1,OC=3,
∴D(0,-1),B(3,0),
设直线BE解析式为y=kx+b,
把B、D两点坐标代入可得,解得.
∴直线BE的解析式为.
【点睛】本题主要考查一次函数的综合应用,涉及非负数的性质、全等三角形的判定和性质、等腰直角三角形的性质、待定系数法等知识点.在(1)中注意非负数的性质的应用,在(2)中构造三角形全等是解题的关键,在(3)中证明三角形全等求得D点坐标是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.7用二元一次方程组确定一次函数表达式
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知y是x的一次函数,下表列出了部分y与x的对应值:
x 0 1 2
y 0 2 a
则a的值为( )
A. B.1 C.3 D.4
2.小明根据某个一次函数关系式填写了如下的表格:其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是( )
-2 0 1
6 2 0
A.-2 B.0 C.2 D.4
3.在一条笔直的公路上A、B两地相120km,甲车从A地开往B地,乙车从B地开往A地,甲比乙先出发.设甲、乙两车距A地的路程为y千米,甲车行驶的时间为x小时,y与x之间的关系如图所示,下列说法错误的是( )
A.甲车的速度比乙的速度慢 B.甲车出发1小时后乙才出发
C.甲车行驶了2.8h或3.2h时,甲、乙两车相距10km D.乙车达到A地时,甲车离A地90km
4.过点(0,0)的直线是( ).
A.y=x-1 B.y=x+2 C.y=-2x D.y=-2x+1
5.已知直线经过点(k,3)和(1,k),则k的值为( )
A. B. C. D.
6.若三点在同一条直线上,则a的值为( )
A.4 B.2 C. D.
7.过原点和点(2,3)的直线的解析式为( )
A.y=x B.y=x C.y=x+1 D.y=-2x+7
8.已知点,,点,过点作轴的平行线交直线于点,则线段的长为( )
A. B. C. D.
9.如图,一次函数的图象分别与轴、轴交于点、,以线段为边在第一象限内作等腰,,则过、两点直线的解析式为( )
A. B. C. D.
10.如图,的顶点,,点C在y轴的正半轴上,,将向左平移得到.若经过点,则点的坐标为( ).
A. B. C. D.
11.已知正比例函数(,为常数),经过点(3,6),以下哪个点不在该正比例函数图象上( )
A.(-3,-6) B.(0,0) C.(1,2) D.(-1,2)
12.在平面直角坐标系中,已知点,点,在x轴上确定点C,使得的周长最小,则点C的坐标是( )
A. B. C. D.
二、填空题
13.已知一次函数图象经过与两点,则该函数的图象与y轴交点的坐标为 .
14.一次函数y=kx+b,当3≤x≤4时,3≤y≤6,则的值是 .
15.已知y与成正比例,且当时,,那么当时,y的值为 .
16.直线与平行,且经过,则 .
17.已知经过点(1,-2)的直线是由向下平移后得到的,那么这条直线的解析式是 .
三、解答题
18.已知y是x的一次函数,且当时,;当时,.
(1)求这个一次函数的表达式;
(2)通过计算,判断点是否在这个函数的图象上?
19.一列火车以的速度匀速前进.求它的行驶路程s(单位:)关于行驶时间t(单位:h)的函数解析式,并画出函数图象.
20.下图是某市轻轨列车两站之间行驶速度v(米/秒)与行驶时间t(秒)之间的函数图象,已知点,点,点.
(1)求线段的函数解析式.
(2)求这两站之间列车速度不低于30米/秒的行驶时间.
21.我们知道,弹簧的总长度是所挂重物的一次函数,请根据如图所示的信息解决问题.
(1)求一次函数表达式;
(2)求弹簧不挂重物时的长度.
22.综合与实践
某班同学分三个小组进行“板凳中的数学”的项目式学习研究,第一小组负责调查板凳的历史及结构特点;第二小组负责研究板凳中蕴含的数学知识:第三小组负责汇报和交流,下面是第三小组汇报的部分内容,请你阅读相关信息,并解答“建立模型”中的问题.
【背景调查】
图①中的板凳又叫“四脚八叉凳”,是中国传统家具,其榫卯结构体现了古人含蓄内敛的审美观.榫眼的设计很有讲究,木工一般用铅笔画出凳面的对称轴,以对称轴为基准向两边各取相同的长度,确定榫眼的位置,如图②所示.板凳的结构设计体现了数学的对称美.
【收集数据】
小组收集了一些板凳并进行了测量.设以对称轴为基准向两边各取相同的长度为,凳面的宽度为,记录如下:
以对称轴为基准向两边各取相同的长度 16.5 19.8 23.1 26.4 29.7
凳面的宽度 115.5 132 148.5 165 181.5
【分析数据】
如图③,小组根据表中x,y的数值,在平面直角坐标系中描出了各点.
【建立模型】
请你帮助小组解决下列问题:
(1)观察上述各点的分布规律,它们是否在同一条直线上?如果在同一条直线上,求出这条直线所对应的函数解析式;如果不在同一条直线上,说明理由.
(2)当凳面宽度为时,以对称轴为基准向两边各取相同的长度是多少?
23.试说明点,,在同一条直线上.
24.在平面直角坐标系中,已知点A(a,0),C(0,b),且a、b满足(a+1)2+=0.
(1)直接写出:a= ,b= .
(2)如图,点B为x轴正半轴上一点,过点B作BEAC于点E,交y轴于点D,连接OE,若OE平分∠AEB,此时,OB与OC有怎样的大小关系?证明你的结论.
(3)在(2)的条件下,求直线BE的解析式.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D D D C B A A C A D
题号 11 12
答案 D C
1.D
【分析】设出一次函数的解析式,采用待定系数法,在表格中选择两个点的坐标代入解析式中,求出解析式,然后再将x=2代入解析式中求出a的值即可.
【详解】解:由题意知,设一次函数的解析式为:
代入点
即,解得
故一次函数的解析式为:
将x=2,y=a时,代入解析式中,解得a=4.
故答案为:D.
【点睛】本题考查用待定系数法求一次函数的解析式,将点的坐标代入解析式中,联立二元一次方程组即可求解.
2.D
【分析】首先根据待定系数法求出一次函数的解析式,然后把x= 1代入,即可求出对应的y值.
【详解】解:设一次函数的解析式为y=kx+b.
把x=0,y=2;x=1,y=0代入,
得,
解得,
∴.
当x= 1时,y=4.
故选D
【点睛】本题考查了待定系数法求一次函数解析式,掌握待定系数法求一次函数解析式是解题的关键.
3.D
【分析】根据图象直接判断A;求出两车的路程y与时间x之间的函数关系式,即可判断B、C、D
【详解】解:当甲出发时乙未出发,甲行驶5小时未到达B地,而乙已经到达A地,说明甲车的速度比乙的速度慢,故选项A正确;
设甲车的路程y与时间x之间的函数关系式为,代入,
得,
解得,
∴甲车的路程y与时间x之间的函数关系式为;
设乙车的路程y与时间x之间的函数关系式为,代入和,
,解得,
∴乙车的路程y与时间x之间的函数关系式为,
当时,,解得,
即甲车出发1小时后乙才出发,故选项B正确;
当时,解得;
当时,解得;
∴甲车行驶了2.8h或3.2h时,甲、乙两车相距10km,故选项C正确;
当时,,故选项D错误;
故选:D.
【点睛】此题考查了一次函数的图象,求一次函数的解析式,一次函数的应用,正确理解一次函数的图象得到相关信息是解题的关键.
4.C
【详解】试题分析:由一次函数的图象和性质可知,图象过原点(0,0),那么一定是正比例函数,在这四个选项中,只有C是正比例函数.
故选C.
考点:一次函数的图象和性质.
5.B
【分析】运用待定系数法求一次函数解析式,代入后求出k,b的值即可.
【详解】∵直线y=kx+b经过点(k,3)和(1,k),
∴将(k,3)和(1,k),代入解析式y=kx+b得:
解得:k=±,b=0,
则k的值为:±.
故选B.
6.A
【分析】设这条直线解析式为,先把B点和C点坐标代入,待定系数法求解析式得出,当时,求得的值,即可求解.
【详解】解:设这条直线解析式为,,
,
解得:,
∴直线解析式为,
将点代入得,,
解得,
故选:A.
【点睛】本题考查了待定系数法求一次函数解析式,求得一次函数解析式是解题的关键.
7.A
【分析】采用待定系数法求解析即可.
【详解】设直线解析式为:
将(0,0),(2,3)代入解析式得:
,解得,
所以直线解析式为:,
故选A.
【点睛】本题考查求函数解析式,熟练掌握待定系数法是关键.
8.C
【分析】先利用待定系数法求出直线AB的解析式,再求出点D坐标,进而可求出CD的长.
【详解】解:设直线AB的解析式为y=kx+b,
将A(﹣1,0)、B(0,﹣3)代入,
得:,解得:,
∴直线AB的解析式为y=﹣3x﹣3,
∵点C(2,﹣2)且CD∥x轴交直线AB于点D,
∴当y=﹣2时,由﹣2=﹣3x﹣3得:x= ,
∴D(,﹣2),
∴CD=2﹣()= ,
故选:C.
【点睛】本题考查待定系数法求一次函数的解析式、坐标与图形,熟练掌握待定系数法求函数的解析式的方法,求出点D坐标是解答的关键.
9.A
【分析】易得OB=3,OA=4,由在等腰中,,得 AOB CDA(AAS),从而得C(7,4),进而根据待定系数法,即可得到答案.
【详解】∵一次函数的图象分别与轴、轴交于点、,
∴A(4,0),B(0,3),
∴OB=3,OA=4,
过点C做CD⊥x轴于点D,
∵在等腰中,,
∴∠OAB+∠CAD=∠OAB+∠ABO,即:∠CAD=∠ABO,
∵AB=AC,∠AOB=∠ADC=90°,
∴ AOB CDA(AAS),
∴CD=AO=4,AD=BO=3,
∴C(7,4),
设直线的解析式为:y=kx+b,
把B(0,3),C(7,4),代入y=kx+b,得,解得:,
∴直线的解析式为:y=x+3,
故选A.
【点睛】本题主要考查一次函数图象与全等三角形的判定与性质定理,掌握“一线三垂直”全等模型,是解题的关键.
10.D
【分析】设点C的坐标为,利用勾股定理分别求出的长,结合,即可求出点C的坐标,求出直线的解析式,即可求出直线的解析式,从而推出直线相当于直线向左平移3个单位得到的,由此即可得到答案.
【详解】解:设点C的坐标为,
则由勾股定理得:,,
∵,
∴,
∴或(舍去),
∴点C的坐标为,
设直线的解析式为,
∴,
∴,
∴直线的解析式为,
∵是经过平移得到的,
∴可设直线的解析式为,
∵经过点,
∴,
∴直线的解析式为,
∴直线相当于直线向左平移3个单位得到的,
∴点是由点C向左平移3个单位得到的,
∴点的坐标为,
故选:D.
【点睛】本题主要考查了一次函数的平移,勾股定理,待定系数法求一次函数解析式等等,熟知一次函数的相关知识是解题的关键.
11.D
【分析】先利用已知点求得正比例函数的解析式,然后每个选项中点代入验证即可.
【详解】解:∵正比例函数(,为常数),经过点(3,6),
∴,解得,
∴正比例函数的解析式为,
把(-3, 6)代入, 6=2×(-3),故选项A在这个函数图象上,
把(0,0)代入,0=2×0,故选项B在这个函数图象上;
把(1,2)代入,2=2×1,故选项C在这个函数图象上;
把(-1,2)代入,2≠2×(-1),故选项D在这个函数图象上;
故选:D
【点睛】此题主要考查了一次函数的性质,以及函数图象上点的坐标特点,待定系数法求一次函数解析式,关键是掌握凡是函数图象经过的点必能满足解析式.
12.C
【分析】因为AB的长度是确定的,故△CAB的周长最小就是CA+CB的值最小,作点A关于x轴的对称点A′,连接A′B交x轴于点C,求出C点坐标即可.
【详解】解:如图,作点A关于x轴的对称点A′,连接A′B交x轴于点C,此时,AC+BC=A′C+BC=AC,长度最小,
∵A(-1,2),
∴A′(-1,﹣2),
设直线A′B的解析式为y=kx+b(k≠0),把A′(-1,﹣2),代入得,
∴,解得,
∴直线A′B的解析式为y=-2x﹣4,
当y=0时,x=-2,
∴C(-2,0).
故选:C
【点睛】本题考查了轴对称-最短路径问题,一次函数与坐标轴交点问题,解题关键是确定点C的位置,利用一次函数解析式求坐标.
13.(0,)
【分析】设一次函数的解析式为y=kx+b,然后把与两点分别代入求出一次函数解析式,进而问题可求解.
【详解】设一次函数的解析式为y=kx+b,
把与两点分别代入得
,
解得:,
所以一次函数的解析式为:,
当x=0时,y=,
所以该函数的图象与y轴交点的坐标为(0,),
故答案为(0,).
【点睛】本题考查了一次函数图象与坐标轴的交点问题,熟练掌握待定系数法是解本题的关键.
14.-2或-5/-5或-2
【分析】由于k的符号不能确定,故应对k>0和k<0两种情况进行解答.
【详解】解:当k>0时,此函数是增函数,
∵当3≤x≤4时,3≤y≤6,
∴当x=3时,y=3;当x=4时,y=6,
∴,解得
∴= 2;
当k<0时,此函数是减函数,
∵当3≤x≤4时,3≤y≤6,
∴当x=3时,y=6;当x=4时,y=3,
∴,解得
∴=-5.
故答案为-2或-5.
【点睛】本题考查的是一次函数的性质,在解答此题时要注意分类讨论,不要漏解.
15.
【分析】
本题考查的是正比例函数,解答本题的关键是熟练掌握正比例函数的一般形式: .由题意设,根据当时,,即可求出k的值,从而得到结果.
【详解】
解:设,
把,,代入得:
,
解得,
∴,
当时,.
故答案为:
16.-3
【分析】根据直线与直线平行得到,把代入即可求出b,即可求解.
【详解】解:∵直线与直线平行
∴
把代入得:
∴
故答案为: .
【点睛】本题考查的是用待定系数法求一次函数的解析式,解答此题的关键是要熟知两直线平行时其未知数的系数相等.
17.y=3x-5
【分析】根据平移规律可知,k=3,则向下平移后得到的解析式为y=3x+b,将(1,-2)代入求解即可.
【详解】解:∵直线是由向下平移后得到的
∴k=3
∴y=3x+b
∵直线经过点(1,-2)
∴-2=3×1+b
∴b=-5
∴y=3x-5
故答案为:y=3x-5
【点睛】本题考查了求一次函数的解析式及平移规律,解题的关键是掌握一次函数平移的规律.
18.(1)y=3x-5;(2)点P(4,6)不在这个函数的图象上.
【分析】(1)设一次函数解析式为y=kx+b,然后用待定系数法求出k、b,即可得到答案;
(2)计算x为4时对应的一次函数值,然后根据一次函数图象上的点的坐标特征进行判断.
【详解】解:(1)设一次函数解析式为y=kx+b,
根据题意得 ,
解得,
∴这个一次函数的表达式为y=3x-5;
(2)∵当x=4时,
y=3x-5=3×4-5=7≠6,
∴点P(4,6)不在这个函数的图象上.
【点睛】本题考查了待定系数法求一次函数解析式,一次函数图象上点的坐标特征,熟练掌握待定系数法是解题的关键.
19..图象见解析
【分析】根据公式路程=速度×时间先列出函数解析式,然后画出函数图象即可.
【详解】解:∵火车以的速度匀速前进,
∴它的行驶路程s(单位:)关于行驶时间t(单位:h)的函数解析式为:.
当时,,
当时,.
作图如下:
【点睛】本题考查列函数解析式,以及画函数图象,掌握画函数图象的方法是解题关键.
20.(1)
(2)秒
【分析】本题主要考查一次函数的应用,熟悉相关的知识是解题的关键;(1)根据待定系数法把点B、点C待入解析式即可求解;(2)求出的解析式,把30代入即可求解.
【详解】(1)解:设线段的解析式为:;
把,代入解析式得:
;
解得:;
∴
(2)设线段的解析式为:;
把代入,得;
∴;
把代入得;
把代入得;
∴列车速度不低于30米/秒的行驶时间为:(秒).
21.(1)
(2)弹簧不挂重物时的长度为
【分析】本题考查了运用待定系数法求一次函数的解析式的运用,由自变量求函数值的运用,解答时求出函数的解析式是关键.
(1)设与的函数关系式为,由待定系数法求出其解即可;
(2)把时代入解析式求出的值即可.
【详解】(1)设,
由图可知:图像经过,
,
解得,
∴一次函数表达式为:;
(2)由题意得,当时,.
答:弹簧不挂重物时的长度为.
22.(1)在同一条直线上,函数解析式为:
(2)
【分析】本题考查了一次函数的实际应用,待定系数法求函数解析式,已知函数值求自变量,熟练掌握知识点,正确理解题意是解题的关键.
(1)用待定系数法求解即可;
(2)将代入函数解析式,解方程即可.
【详解】(1),
解:设函数解析式为:,
∵当,,
∴,
解得:,
∴函数解析式为:,
经检验其余点均在直线上,
∴函数解析式为,这些点在同一条直线上;
(2)解:把代入得:
,
解得:,
∴当凳面宽度为时,以对称轴为基准向两边各取相同的长度为.
23.见解析
【分析】本题主要考查了一次函数的性质,求一次函数解析式,用待定系数法先求出过任意两点的一次函数解析式,再把另外一个点代入,如果成立,就三点共线.
【详解】证明:设经过点,的函数解析式为,则:
,
解得:,
∴直线的解析式为:,
把代入得:,
∴在直线上,
∴三点在同一条直线上.
24.(1)﹣1,﹣3
(2)OB=OC,证明见解析
(3)
【分析】(1)利用非负数的性质可求得a、b的值;
(2)过O作OF⊥OE,可得△OEF为等腰直角三角形,可证明△EOC≌△FOB,可证明OB=OC;
(3)可证明△AOC≌△DOB,可求得D点坐标,由(2)可求得B点坐标,从而可求得直线BE的解析.
【详解】(1)解:∵(a+1)2+=0,
∴a+1=0,b+3=0,
∴a=-1,b=-3,
故答案为:-1;-3;
(2)解:OB=OC,证明如下:
如图,过O作OF⊥OE,交BE于F,
∵BE⊥AC,OE平分∠AEB,
∴△EOF为等腰直角三角形,
∴∠EOC+∠DOF=∠DOF+∠FOB=90°,
∴∠EOC=∠FOB,且∠OEC=∠OFB=135°,
在△EOC和△FOB中,,
∴△EOC≌△FOB(ASA),
∴OB=OC;
(3)解:∵△EOC≌△FOB,
∴∠OCE=∠OBE,OB=OC,
在△AOC和△DOB中,
,
∴△AOC≌△DOB(ASA),
∴OD=OA,
∵A(-1,0),C(0,-3),
∴OD=1,OC=3,
∴D(0,-1),B(3,0),
设直线BE解析式为y=kx+b,
把B、D两点坐标代入可得,解得.
∴直线BE的解析式为.
【点睛】本题主要考查一次函数的综合应用,涉及非负数的性质、全等三角形的判定和性质、等腰直角三角形的性质、待定系数法等知识点.在(1)中注意非负数的性质的应用,在(2)中构造三角形全等是解题的关键,在(3)中证明三角形全等求得D点坐标是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
