7.1为什么要证明同步练习(含解析)
文档属性
| 名称 | 7.1为什么要证明同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 536.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-15 08:38:38 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
7.1为什么要证明
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.9人分24张票,每人至少1张,则( )
A.至少有3人票数相等 B.至少有4人票数无异
C.不会有5人票数一致 D.不会有6人票数同样
2.张大伯在中国银行存入10000元人民币,并在存单上留下了6位数的密码,每个数字都是0﹣9这十个数字中的一
个,但由于年龄的缘故,张大伯忘记了密码中间的两个数字,那么张大伯最多可能实验多少次,才能正确输入密码( )
A.1次 B.50次 C.100次 D.200次
3.100人共有2000元人民币,其中任意10人的钱数的和不超过380元.那么一个人最多有( )元.
A.216 B.218 C.238 D.236
4.已知上海到美国洛杉矶的海底电缆共有15个接点.某次从上海发出一个信息时,某个接点发生故障,为了尽快断定故障发生点,排除故障,至少需要检查的接点个数是( )
A.3 B.4 C.5 D.6
5.图中小圆圈表示网络的结点,结点之间的连接表示它们有网线相连,相连标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,若信息可以分开沿不同路线同时传递,则单位时间内传递的最大信息量为( )
A.11 B.10 C.8 D.7
6.世界杯足球赛小组赛,每个小组4个队进行单循环比赛,每场比赛胜队得3分,败队得0分,平局时两队各得1分,小组赛完以后,总积分最高的两个队出线进入下轮比赛,如果总积分相同,还要按净胜球排序,一个队要保证出线,这个队至少要积( )
A.6分 B.7分 C.8分 D.9分
7.如图,点A1,A2,A3,A4是某市正方形道路网的部分交汇点,且它们都位于同一对角线上.某人从点A1出发,规定向右或向下行走,那么到达点A3的走法共有( )
A.4种 B.6种 C.8种 D.10种
8.试说明“若,,,则”是真命题.以下是排乱的推理过程:
①因为(已知);
②因为,(已知);
③所以,(等式的性质);
④所以(等量代换);
⑤所以(等量代换).
正确的顺序是( )
A.①→③→②→⑤→④ B.②→③→⑤→①→④
C.②→③→①→⑤→④ D.②→⑤→①→③→④
9.小明中午放学回家自己煮面条吃,有下面几道工序:(1)洗锅盛水2分钟;(2)洗菜3分钟;(3)准备面条及佐料2分钟;(4)用锅把水烧开7分钟;(5)用烧开的水煮面条和菜要3分钟.以上各工序除(4)外,一次只能进行一道工序,小明要将面条煮好,最少用( )
A.14分钟 B.13分钟 C.12分钟 D.11分钟
10.绍兴一中新来了三位年轻老师,蔡老师、朱老师、孙老师,他们每人分别教生物、物理、英语、政治、历史和数学六科中的两科课程.其中,三个人有以下关系:
①物理老师和政治老师是邻居;
②蔡老师在三人中年龄最小;
③孙老师、生物老师和政治老师三人经常一起从学校回家;
④生物老师比数学老师年龄要大些;
⑤在双休日,英语老师、数学老师和蔡老师三人经常一起打排球.
根据以上条件,可以推出朱老师可能教( )
A.历史和生物 B.物理和数学 C.英语和生物 D.政治和数学
11.下列结论,你能肯定的是( )
A.今天是阴天,明天必然还是阴天
B.三个连续整数的积一定能被6整除
C.小明的数学成绩一向很好,因而后天的竞赛考试中他必然能获得一等奖
D.两张照片看起来完全一样,可以知道这两张必然是同一张底片冲洗出来的
12.图(①)为雅婷左手拿着3张深灰色与2张浅灰色的牌迭在一起的情形.以下是她每次洗牌的三个步骤:
步骤一:用右手拿出迭在最下面的2张牌,如图(②).
步骤二:将右手拿的2张牌依序交错插入左手拿的3张牌之间,如图(③).
步骤三:用左手拿着颜色顺序已改变的5张牌,如图(④).
若依上述三个步骤洗牌,从图(①)的情形开始洗牌若干次后,其颜色顺序会再次与图(①)相同,则洗牌次数可能为下列何者?( )
A.18 B.20 C.25 D.27
二、填空题
13.甲、乙、丙三位同学踢球时,不小心将班级的玻璃打破,当班主任追问时,甲说:“是丙打破的.”乙说:“不是我打破的.”丙说:“甲说谎.”三个人中只有一人说了真话,请你判断:玻璃是 打破的.
14.字母a,b,c,d各代表正方形、线段、正三角形、圆四个图形中的一种,将它们两两组合,并用字母连接表示,如表是三种组合与连接的对应表,由此可推断图形的连接方式为 .
组合
连接
15.如图,点P是直线l外一点,过点P画直线,,,分别交已知直线l于点A,B,C,请你用量角器量,,的度数,并量线段,,的长度,你发现的规律是 .
16.从小明家到学校有三条路,如图所示,小明想尽快从家赶到学校,应走路线 ,理由: .
17.在乒乓球比赛中是没有平局的,都要分出胜负,甲、乙、丙三人进行乒乓球比赛,其中甲胜4局负2局,乙胜3局负3局,若丙负了3局,则丙胜了 局.
三、解答题
18.(1)计算并观察下列各式:
①
②
③
(2)已知,那么_________.
(3)从上述过程中你发现了什么规律?请用含的代数式表示出来,并说明理由.
19.命题:“在角的平分线上的点到这个角的两边的距离相等”
对于此命题作出图形,写出已知和求证,并证明之.
已知:____________________________________
求证:________________________
作图:
证明:
20.已知以下基本事实:①对顶角相等;②一条直线截两条平行线所得的同位角相等;③两条直线被第三条直线所截,若同位角相等,则这两条直线平行;④经过直线外一点,有且只有一条直线平行于已知直线.
(1)在利用以上基本事实作为依据来证明命题“两直线平行,内错角相等”时,必须要用的基本事实有____(填入序号即可);
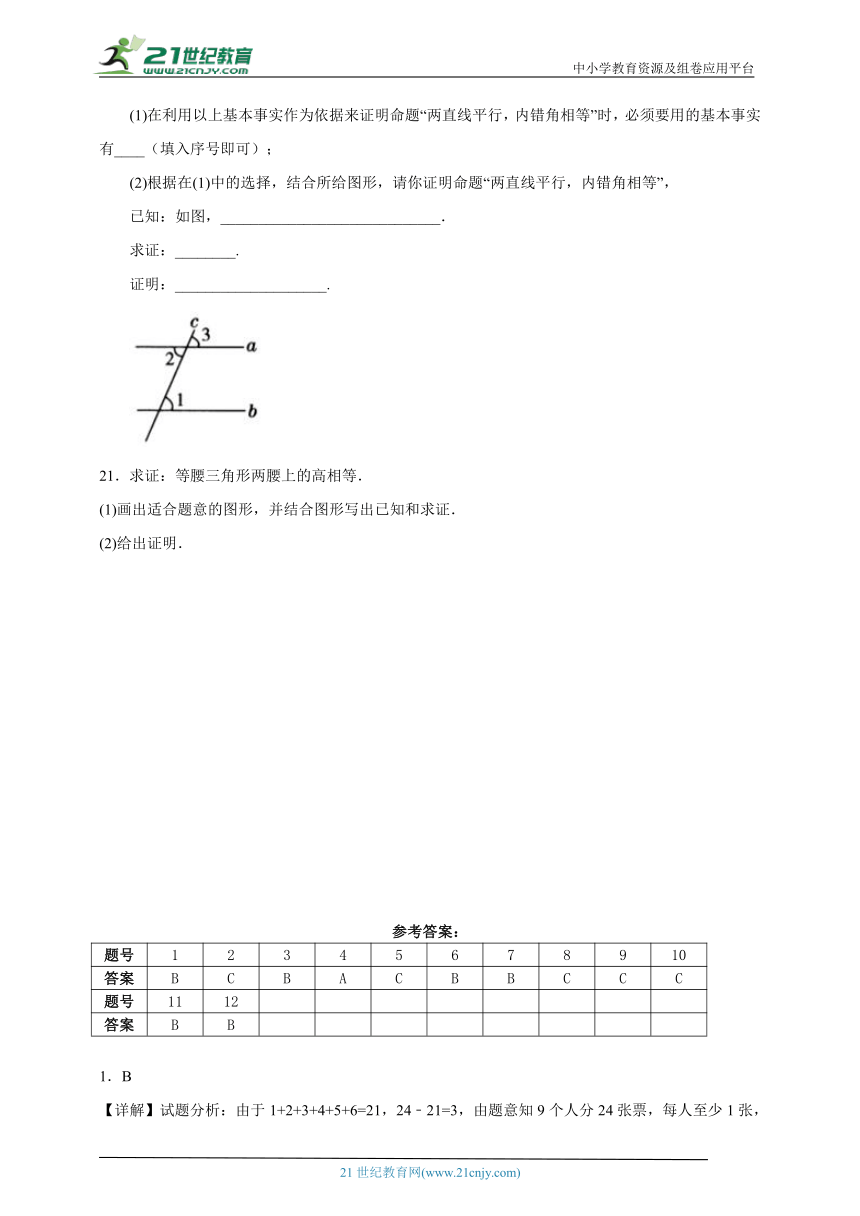
(2)根据在(1)中的选择,结合所给图形,请你证明命题“两直线平行,内错角相等”,
已知:如图,_____________________________.
求证:________.
证明:____________________.
21.求证:等腰三角形两腰上的高相等.
(1)画出适合题意的图形,并结合图形写出已知和求证.
(2)给出证明.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B A C B B C C C
题号 11 12
答案 B B
1.B
【详解】试题分析:由于1+2+3+4+5+6=21,24﹣21=3,由题意知9个人分24张票,每人至少1张,而且票必须分完,则每人票数不相等的情况最多6种可能,依此求解.
解:由题意知9个人分24张同样的足球票,每人至少1张,而且票必须分完,
∵1+2+3+4+5+6=21,24﹣21=3,
∴每人票数不相等的情况最多6种可能,
∴满足条件的分法是至少有4人票数无异.
故选B.
点评:本题主要考查了推理与论证的方法,关键是得出每人票数不相等的最多情况数,难度适中.
2.C
【详解】试题分析:得到中间两个空数的可能情况即可.
解:∵0﹣9这个十个数字中任取两个组合共有100种取法,
∴王大伯最多可能试验100次,才能正确输入密码.
故选C.
点评:此题主要考查了推理与论证,解决本题的关键是得到0﹣9这个十个数字中任取两个组合共有100种取法.
3.B
【详解】试题分析:由于共有2000元人民币,10人不超过380元,则其余90人钱数的和不少于1620元,再根据抽屉原理可知存在9人的钱数的和不少于162元,
解:任意10个人的钱数的和不超过380元,(1)
∴任意90个人的钱数的和不少于1620元,
由抽屉原理,存在9人的钱数的和不少于162元,(2)
(1)﹣(2),一个人最多能有218元.
故选B.
点评:本题考查了推理与论证,解答此题要熟悉抽屉原理﹣﹣﹣﹣把多于kn个东西任意分放进n个空抽屉(k是正整数),那么一定有一个抽屉中放进了至少k+1个东西.
4.A
【详解】试题分析:可以先检查中间的接点,以此类推.
解:①7、1、7;
②3、1、3;
③1、1、1.
故至少需要检查的接点个数是3个.
故选A.
点评:此题注意从中间开始.
5.C
【详解】试题分析:先找出从结点A向结点B传递信息可沿A﹣C﹣B和A﹣D﹣B路线同时传递,再找出每条路线通过的最大信息量,然后相加即可得到答案.
解:由于信息可以分开沿不同路线同时传递,所以从结点A向结点B传递信息可经过结点D和结点B;又因为从结点A到结点D的最大信息量为5,从结点C到结点B的最大信息量为3,所以从结点A向结点B传递信息,若信息可以分开沿不同路线同时传递,则单位时间内传递的最大信息量为5+3=8.
故选C.
点评:本题考查了推理与论证的方法:先分析题目所给的条件或要求,然后通过推理得到相关的结论.
6.B
【分析】根据题意可得小组赛的总场数为小组数×(小组数﹣1)÷2,可得3个队的总积分,进而分类讨论小组得6分或7分能否出线即可.
【详解】解:根据题意得:4个队单循环比赛共比赛4×3÷2=6场,
每场比赛后两队得分之和或为2分(即打平),或为3分(有胜负),
所以6场后各队的得分之和不超过18分,
①若一个队得7分,剩下的3个队得分之和不超过11分,不可能有两个队得分之和大于或等于7分,所以这个队必定出线,
②如果一个队得6分,则有可能还有两个队均得6分,而净胜球比该队多,该队仍不能出线.
故选B.
【点睛】本题考查了比赛问题中的推理与论证;得到比赛的总场数以及相应的总积分是解决本题的突破点;分类探讨可以出线的小组的最低分是解决本题的难点.
7.B
【详解】试题分析:(1)先向右走,①向右走两个单位,再向下走两个单位到达A3;
②向右走一个单位,再向下走一个单位,再向右走一个单位,再向下走一个单位,到达A3;
③向右走一个单位,向下走两个单位,再向右走一个单位,到达A3;
(2)先向下走,①向下走两个单位,再向右走两个单位到达A3;
②向下走一个单位,再向右走一个单位,再向下走一个单位,再向右走一个单位,到达A3;
③向下走一个单位,向右走两个单位,再向下走一个单位,到达A3;
因此本题共有6种走法.
解:如图,从A1到大A3共有6种走法,故选B.
点评:本题应分类讨论,然后依次找出合理的路线,以免漏解.
8.C
【分析】写出正确的推理过程,进行排序即可.
【详解】证明:因为,(已知),
所以,(等式的性质);
因为(已知),
所以(等量代换).
所以(等量代换).
∴排序顺序为:②→③→①→⑤→④.
故选C.
【点睛】本题考查推理过程.熟练掌握推理过程,是解题的关键.
9.C
【分析】本题考查了时间统筹;根据统筹方法,烧开水时可洗菜和准备面条及佐料,这样可以节省时间,所以小明所用时间最少为(1)、(4)、(5)步时间之和.解决问题的关键是读懂题意,采用统筹方法是生活中常用的有效节省时间的方法,本题将数学知识与生活相结合,是一道好题.
【详解】解:第一步,洗锅盛水花2分钟;
第二步,用锅把水烧开7分钟,同时洗菜3分钟,准备面条及佐料2分钟,总计7分钟;
第三步,用烧开的水煮面条和菜要3分钟;
总计共用:(分钟),
故选:C.
10.C
【详解】试题分析:由②④⑤可得蔡老师一定不教生物、英语和数学,进而得到蔡老师可能教物理、政治、历史,由①可知蔡老师一定教历史;
由③可得孙老师一定不教生物和政治,蔡老师一定教历史,因此孙老师可能教物理、英语、和数学,英语和数学不是一个人教,因此孙老师一定教物理;
有以上分析可得朱老师可能教生物、英语、和数学,英语和数学不是一个人教,每个老师又教两科,因此朱老师一定教生物,结合选项可选出答案.
解:由②④可得蔡老师一定不教生物;由⑤可得蔡老师不教英语和数学,因此蔡老师可能教物理、政治、历史,由①可知物理老师和政治老师不是同一个人,因此蔡老师一定教历史;
由③可得孙老师一定不教生物和政治,因为蔡老师一定教历史,因此孙老师可能教物理、英语、和数学,由⑤可知英语和数学不是一个人教,因此孙老师一定教物理,因此蔡老师一定教历史和政治;
由于孙老师一定教物理,因此蔡老师一定教历史和政治,因此朱老师可能教生物、英语、和数学,因为由⑤可知英语和数学不是一个人教,每个老师又教两科,因此朱老师一定教生物,结合选项可得一定从A、C中选,
又因为蔡老师一定教历史,因此A不合要求只能选C,朱老师可能教英语和生物,
故选C.
点评:此题主要考查了推理论证,关键是正确判断出每个老师一定不教哪一科,一定教哪一科,根据矛盾关系确定答案.
11.B
【分析】判断命题的真假即可得到答案.
【详解】解:三个连续整数中一定有一个是2的倍数、一个是3的倍数,所以它们的积一定能被6整除,故B项正确.A项、C项、D项都是猜测的结论,不能说明一定成立.
故选B.
【点睛】本题考查命题的真假,解题的关键是对每个选项进行合理分析.
12.B
【详解】试题分析:根据洗牌的规则得出洗牌的变化规律,进而根据各选项分析得出即可.
解:设5张牌分别为:1,2,3,A,B;第1次洗牌后变为:1,A,2,B,3;
第2次洗牌后变为:1,B,A,3,2;
第3次洗牌后变为:1,3,B,2,A;
第4次洗牌后变为:1,2,3,A,B;
故每洗牌4次,其颜色顺序会再次与图(①)相同,
故洗牌次数可能的数为4的倍数,选项中只有20符合要求.
故选B.
点评:此题主要考查了推理与论证,根据已知得出洗牌的变化规律是解题关键.
13.乙
【分析】本题须分别分析甲、乙、丙三人说的话,再根据三人中只有一人说的是真话,进行推理即可得出结论.
【详解】解:根据题意可得:玻璃是乙打破的
∵此时乙说:“不是我打破的”则乙说的是假话
甲说:“是丙打破的”也是假话,
则丙说:“甲说谎”是真话,
∴玻璃是乙打破的符合题意
故答案为乙
【点睛】本题考查推理与论证,在解题时要能根据题意进行推理与论证得出正确答案是本题的关键.
14.
【分析】首先根据已知图形中两个图形中共同含有的图形,就可以判断每个符号所代表的图形,即可得出结论.
【详解】解:结合题表中前两个图可以看出:b代表正方形;
结合后两个图可以看出:d代表圆;
因此a代表线段,c代表三角形,
所以图形的连接方式为:.
故答案为.
【点睛】本题主要考查推理与论证,观察、分析识别图形的能力;解决此题的关键是通过观察图形确定a,b,c,d各代表什么图形.
15.随着度数的增大,线段的长度减小
【分析】本题考查了度量线段,度量角度,角度大小的比较,会使用度量工具度量是解题的关键.
使用量角器度量角度,带刻度的直尺度量线段的长度,根据度量的数据分析角度和长度之间的关系即可.
【详解】解:量得,,
∴在P点与直线上的点的连线中,与直线的夹角越大(不超过),P点与直线交点连线的线段长度越短.
故答案为:随着度数的增大,线段的长度减小.
16. , 两点之间线段最短.
【分析】根据线段的性质:两点之间线段最短作答.
【详解】解:小明从家到学校有3条路走,他走最近的路线是路线a.其道理为:两点之间线段最短.
故答案为(1). , (2). 两点之间线段最短.
【点睛】本题考查线段的性质:两点之间线段最短.
17.1
【分析】结合实际我们知道,有人胜一局,便有人负一局,那么最后胜局的总数应该等于负数的总局,据此作答即可.
【详解】解:总负局数为 2+3+3=8,
而甲、乙胜局数为4+3=7 ,
故丙胜局数为8-7=1.
故答案为1.
【点睛】本题考查有理数的混合运算,解题的关键是掌握有理数的混合运算法则.
18.(1))①64,63 ; ②25,24 ; ③4.41,3.41;(2)404495;(3),见解析.
【分析】(1)根据一般数据的计算进行解答即可;
(2)从(1)中找出规律,的值比的值相差1即可;
(3)从(1)和(2)中得出规律:.
【详解】解:(1)①64 63 ②25 24 ③4.41 3.41;
(2)已知,那么404495;
(3)从以上过程中,发现的规律是:.
理由如下:
根据平方差公式,得 .
【点睛】本题考查平方差公式,解题的关键是找出其中的规律进行解答.
19.见解析
【分析】先写出已知,求证,画出图形,再证明,即可.
【详解】已知:如图,是的平分线,点P为上任意一点,且,垂足分别为E,F.
求证:.
作图:
证明:∵是的平分线,
∴,
∵,
∴,
在和中,
,
∴,
∴.
【点睛】本题主要考查了全等三角形的判定和性质,解题的关键是证明三角形全等.
20.详见解析.
【详解】试题分析:(1)利用图示:根据平行线的性质,证明“两直线平行,内错角相等”的过程解答;
(2)根据“两直线a∥b,判定同位角∠1=∠3”,然后由对顶角∠3=∠2及等量代换证得
∠1=∠2.
试题解析:
(1)①②;(2)已知:a∥b,直线a、b被直线c所截.
求证:∠1=∠2.
证明:∵a∥b,∴∠1=∠3.
∵∠3 =∠2,∴∠1 =∠2.
21.(1)见解析
(2)见解析
【分析】(1)根据题意画出图形,写出已知和求证即可;
(2)通过角角边证明两个含高的三角形全等,从而得出对应边(高)相等.
【详解】(1)解:已知:如图,中,于点D,于点E.
求证:.
(2)证明:于点D,于点E,
,
,
∴,
∴.
【点睛】本题考查全等三角形在证明三角形两腰上的高相等的应用,掌握角角边的证明方法是本题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
7.1为什么要证明
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.9人分24张票,每人至少1张,则( )
A.至少有3人票数相等 B.至少有4人票数无异
C.不会有5人票数一致 D.不会有6人票数同样
2.张大伯在中国银行存入10000元人民币,并在存单上留下了6位数的密码,每个数字都是0﹣9这十个数字中的一
个,但由于年龄的缘故,张大伯忘记了密码中间的两个数字,那么张大伯最多可能实验多少次,才能正确输入密码( )
A.1次 B.50次 C.100次 D.200次
3.100人共有2000元人民币,其中任意10人的钱数的和不超过380元.那么一个人最多有( )元.
A.216 B.218 C.238 D.236
4.已知上海到美国洛杉矶的海底电缆共有15个接点.某次从上海发出一个信息时,某个接点发生故障,为了尽快断定故障发生点,排除故障,至少需要检查的接点个数是( )
A.3 B.4 C.5 D.6
5.图中小圆圈表示网络的结点,结点之间的连接表示它们有网线相连,相连标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,若信息可以分开沿不同路线同时传递,则单位时间内传递的最大信息量为( )
A.11 B.10 C.8 D.7
6.世界杯足球赛小组赛,每个小组4个队进行单循环比赛,每场比赛胜队得3分,败队得0分,平局时两队各得1分,小组赛完以后,总积分最高的两个队出线进入下轮比赛,如果总积分相同,还要按净胜球排序,一个队要保证出线,这个队至少要积( )
A.6分 B.7分 C.8分 D.9分
7.如图,点A1,A2,A3,A4是某市正方形道路网的部分交汇点,且它们都位于同一对角线上.某人从点A1出发,规定向右或向下行走,那么到达点A3的走法共有( )
A.4种 B.6种 C.8种 D.10种
8.试说明“若,,,则”是真命题.以下是排乱的推理过程:
①因为(已知);
②因为,(已知);
③所以,(等式的性质);
④所以(等量代换);
⑤所以(等量代换).
正确的顺序是( )
A.①→③→②→⑤→④ B.②→③→⑤→①→④
C.②→③→①→⑤→④ D.②→⑤→①→③→④
9.小明中午放学回家自己煮面条吃,有下面几道工序:(1)洗锅盛水2分钟;(2)洗菜3分钟;(3)准备面条及佐料2分钟;(4)用锅把水烧开7分钟;(5)用烧开的水煮面条和菜要3分钟.以上各工序除(4)外,一次只能进行一道工序,小明要将面条煮好,最少用( )
A.14分钟 B.13分钟 C.12分钟 D.11分钟
10.绍兴一中新来了三位年轻老师,蔡老师、朱老师、孙老师,他们每人分别教生物、物理、英语、政治、历史和数学六科中的两科课程.其中,三个人有以下关系:
①物理老师和政治老师是邻居;
②蔡老师在三人中年龄最小;
③孙老师、生物老师和政治老师三人经常一起从学校回家;
④生物老师比数学老师年龄要大些;
⑤在双休日,英语老师、数学老师和蔡老师三人经常一起打排球.
根据以上条件,可以推出朱老师可能教( )
A.历史和生物 B.物理和数学 C.英语和生物 D.政治和数学
11.下列结论,你能肯定的是( )
A.今天是阴天,明天必然还是阴天
B.三个连续整数的积一定能被6整除
C.小明的数学成绩一向很好,因而后天的竞赛考试中他必然能获得一等奖
D.两张照片看起来完全一样,可以知道这两张必然是同一张底片冲洗出来的
12.图(①)为雅婷左手拿着3张深灰色与2张浅灰色的牌迭在一起的情形.以下是她每次洗牌的三个步骤:
步骤一:用右手拿出迭在最下面的2张牌,如图(②).
步骤二:将右手拿的2张牌依序交错插入左手拿的3张牌之间,如图(③).
步骤三:用左手拿着颜色顺序已改变的5张牌,如图(④).
若依上述三个步骤洗牌,从图(①)的情形开始洗牌若干次后,其颜色顺序会再次与图(①)相同,则洗牌次数可能为下列何者?( )
A.18 B.20 C.25 D.27
二、填空题
13.甲、乙、丙三位同学踢球时,不小心将班级的玻璃打破,当班主任追问时,甲说:“是丙打破的.”乙说:“不是我打破的.”丙说:“甲说谎.”三个人中只有一人说了真话,请你判断:玻璃是 打破的.
14.字母a,b,c,d各代表正方形、线段、正三角形、圆四个图形中的一种,将它们两两组合,并用字母连接表示,如表是三种组合与连接的对应表,由此可推断图形的连接方式为 .
组合
连接
15.如图,点P是直线l外一点,过点P画直线,,,分别交已知直线l于点A,B,C,请你用量角器量,,的度数,并量线段,,的长度,你发现的规律是 .
16.从小明家到学校有三条路,如图所示,小明想尽快从家赶到学校,应走路线 ,理由: .
17.在乒乓球比赛中是没有平局的,都要分出胜负,甲、乙、丙三人进行乒乓球比赛,其中甲胜4局负2局,乙胜3局负3局,若丙负了3局,则丙胜了 局.
三、解答题
18.(1)计算并观察下列各式:
①
②
③
(2)已知,那么_________.
(3)从上述过程中你发现了什么规律?请用含的代数式表示出来,并说明理由.
19.命题:“在角的平分线上的点到这个角的两边的距离相等”
对于此命题作出图形,写出已知和求证,并证明之.
已知:____________________________________
求证:________________________
作图:
证明:
20.已知以下基本事实:①对顶角相等;②一条直线截两条平行线所得的同位角相等;③两条直线被第三条直线所截,若同位角相等,则这两条直线平行;④经过直线外一点,有且只有一条直线平行于已知直线.
(1)在利用以上基本事实作为依据来证明命题“两直线平行,内错角相等”时,必须要用的基本事实有____(填入序号即可);
(2)根据在(1)中的选择,结合所给图形,请你证明命题“两直线平行,内错角相等”,
已知:如图,_____________________________.
求证:________.
证明:____________________.
21.求证:等腰三角形两腰上的高相等.
(1)画出适合题意的图形,并结合图形写出已知和求证.
(2)给出证明.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B A C B B C C C
题号 11 12
答案 B B
1.B
【详解】试题分析:由于1+2+3+4+5+6=21,24﹣21=3,由题意知9个人分24张票,每人至少1张,而且票必须分完,则每人票数不相等的情况最多6种可能,依此求解.
解:由题意知9个人分24张同样的足球票,每人至少1张,而且票必须分完,
∵1+2+3+4+5+6=21,24﹣21=3,
∴每人票数不相等的情况最多6种可能,
∴满足条件的分法是至少有4人票数无异.
故选B.
点评:本题主要考查了推理与论证的方法,关键是得出每人票数不相等的最多情况数,难度适中.
2.C
【详解】试题分析:得到中间两个空数的可能情况即可.
解:∵0﹣9这个十个数字中任取两个组合共有100种取法,
∴王大伯最多可能试验100次,才能正确输入密码.
故选C.
点评:此题主要考查了推理与论证,解决本题的关键是得到0﹣9这个十个数字中任取两个组合共有100种取法.
3.B
【详解】试题分析:由于共有2000元人民币,10人不超过380元,则其余90人钱数的和不少于1620元,再根据抽屉原理可知存在9人的钱数的和不少于162元,
解:任意10个人的钱数的和不超过380元,(1)
∴任意90个人的钱数的和不少于1620元,
由抽屉原理,存在9人的钱数的和不少于162元,(2)
(1)﹣(2),一个人最多能有218元.
故选B.
点评:本题考查了推理与论证,解答此题要熟悉抽屉原理﹣﹣﹣﹣把多于kn个东西任意分放进n个空抽屉(k是正整数),那么一定有一个抽屉中放进了至少k+1个东西.
4.A
【详解】试题分析:可以先检查中间的接点,以此类推.
解:①7、1、7;
②3、1、3;
③1、1、1.
故至少需要检查的接点个数是3个.
故选A.
点评:此题注意从中间开始.
5.C
【详解】试题分析:先找出从结点A向结点B传递信息可沿A﹣C﹣B和A﹣D﹣B路线同时传递,再找出每条路线通过的最大信息量,然后相加即可得到答案.
解:由于信息可以分开沿不同路线同时传递,所以从结点A向结点B传递信息可经过结点D和结点B;又因为从结点A到结点D的最大信息量为5,从结点C到结点B的最大信息量为3,所以从结点A向结点B传递信息,若信息可以分开沿不同路线同时传递,则单位时间内传递的最大信息量为5+3=8.
故选C.
点评:本题考查了推理与论证的方法:先分析题目所给的条件或要求,然后通过推理得到相关的结论.
6.B
【分析】根据题意可得小组赛的总场数为小组数×(小组数﹣1)÷2,可得3个队的总积分,进而分类讨论小组得6分或7分能否出线即可.
【详解】解:根据题意得:4个队单循环比赛共比赛4×3÷2=6场,
每场比赛后两队得分之和或为2分(即打平),或为3分(有胜负),
所以6场后各队的得分之和不超过18分,
①若一个队得7分,剩下的3个队得分之和不超过11分,不可能有两个队得分之和大于或等于7分,所以这个队必定出线,
②如果一个队得6分,则有可能还有两个队均得6分,而净胜球比该队多,该队仍不能出线.
故选B.
【点睛】本题考查了比赛问题中的推理与论证;得到比赛的总场数以及相应的总积分是解决本题的突破点;分类探讨可以出线的小组的最低分是解决本题的难点.
7.B
【详解】试题分析:(1)先向右走,①向右走两个单位,再向下走两个单位到达A3;
②向右走一个单位,再向下走一个单位,再向右走一个单位,再向下走一个单位,到达A3;
③向右走一个单位,向下走两个单位,再向右走一个单位,到达A3;
(2)先向下走,①向下走两个单位,再向右走两个单位到达A3;
②向下走一个单位,再向右走一个单位,再向下走一个单位,再向右走一个单位,到达A3;
③向下走一个单位,向右走两个单位,再向下走一个单位,到达A3;
因此本题共有6种走法.
解:如图,从A1到大A3共有6种走法,故选B.
点评:本题应分类讨论,然后依次找出合理的路线,以免漏解.
8.C
【分析】写出正确的推理过程,进行排序即可.
【详解】证明:因为,(已知),
所以,(等式的性质);
因为(已知),
所以(等量代换).
所以(等量代换).
∴排序顺序为:②→③→①→⑤→④.
故选C.
【点睛】本题考查推理过程.熟练掌握推理过程,是解题的关键.
9.C
【分析】本题考查了时间统筹;根据统筹方法,烧开水时可洗菜和准备面条及佐料,这样可以节省时间,所以小明所用时间最少为(1)、(4)、(5)步时间之和.解决问题的关键是读懂题意,采用统筹方法是生活中常用的有效节省时间的方法,本题将数学知识与生活相结合,是一道好题.
【详解】解:第一步,洗锅盛水花2分钟;
第二步,用锅把水烧开7分钟,同时洗菜3分钟,准备面条及佐料2分钟,总计7分钟;
第三步,用烧开的水煮面条和菜要3分钟;
总计共用:(分钟),
故选:C.
10.C
【详解】试题分析:由②④⑤可得蔡老师一定不教生物、英语和数学,进而得到蔡老师可能教物理、政治、历史,由①可知蔡老师一定教历史;
由③可得孙老师一定不教生物和政治,蔡老师一定教历史,因此孙老师可能教物理、英语、和数学,英语和数学不是一个人教,因此孙老师一定教物理;
有以上分析可得朱老师可能教生物、英语、和数学,英语和数学不是一个人教,每个老师又教两科,因此朱老师一定教生物,结合选项可选出答案.
解:由②④可得蔡老师一定不教生物;由⑤可得蔡老师不教英语和数学,因此蔡老师可能教物理、政治、历史,由①可知物理老师和政治老师不是同一个人,因此蔡老师一定教历史;
由③可得孙老师一定不教生物和政治,因为蔡老师一定教历史,因此孙老师可能教物理、英语、和数学,由⑤可知英语和数学不是一个人教,因此孙老师一定教物理,因此蔡老师一定教历史和政治;
由于孙老师一定教物理,因此蔡老师一定教历史和政治,因此朱老师可能教生物、英语、和数学,因为由⑤可知英语和数学不是一个人教,每个老师又教两科,因此朱老师一定教生物,结合选项可得一定从A、C中选,
又因为蔡老师一定教历史,因此A不合要求只能选C,朱老师可能教英语和生物,
故选C.
点评:此题主要考查了推理论证,关键是正确判断出每个老师一定不教哪一科,一定教哪一科,根据矛盾关系确定答案.
11.B
【分析】判断命题的真假即可得到答案.
【详解】解:三个连续整数中一定有一个是2的倍数、一个是3的倍数,所以它们的积一定能被6整除,故B项正确.A项、C项、D项都是猜测的结论,不能说明一定成立.
故选B.
【点睛】本题考查命题的真假,解题的关键是对每个选项进行合理分析.
12.B
【详解】试题分析:根据洗牌的规则得出洗牌的变化规律,进而根据各选项分析得出即可.
解:设5张牌分别为:1,2,3,A,B;第1次洗牌后变为:1,A,2,B,3;
第2次洗牌后变为:1,B,A,3,2;
第3次洗牌后变为:1,3,B,2,A;
第4次洗牌后变为:1,2,3,A,B;
故每洗牌4次,其颜色顺序会再次与图(①)相同,
故洗牌次数可能的数为4的倍数,选项中只有20符合要求.
故选B.
点评:此题主要考查了推理与论证,根据已知得出洗牌的变化规律是解题关键.
13.乙
【分析】本题须分别分析甲、乙、丙三人说的话,再根据三人中只有一人说的是真话,进行推理即可得出结论.
【详解】解:根据题意可得:玻璃是乙打破的
∵此时乙说:“不是我打破的”则乙说的是假话
甲说:“是丙打破的”也是假话,
则丙说:“甲说谎”是真话,
∴玻璃是乙打破的符合题意
故答案为乙
【点睛】本题考查推理与论证,在解题时要能根据题意进行推理与论证得出正确答案是本题的关键.
14.
【分析】首先根据已知图形中两个图形中共同含有的图形,就可以判断每个符号所代表的图形,即可得出结论.
【详解】解:结合题表中前两个图可以看出:b代表正方形;
结合后两个图可以看出:d代表圆;
因此a代表线段,c代表三角形,
所以图形的连接方式为:.
故答案为.
【点睛】本题主要考查推理与论证,观察、分析识别图形的能力;解决此题的关键是通过观察图形确定a,b,c,d各代表什么图形.
15.随着度数的增大,线段的长度减小
【分析】本题考查了度量线段,度量角度,角度大小的比较,会使用度量工具度量是解题的关键.
使用量角器度量角度,带刻度的直尺度量线段的长度,根据度量的数据分析角度和长度之间的关系即可.
【详解】解:量得,,
∴在P点与直线上的点的连线中,与直线的夹角越大(不超过),P点与直线交点连线的线段长度越短.
故答案为:随着度数的增大,线段的长度减小.
16. , 两点之间线段最短.
【分析】根据线段的性质:两点之间线段最短作答.
【详解】解:小明从家到学校有3条路走,他走最近的路线是路线a.其道理为:两点之间线段最短.
故答案为(1). , (2). 两点之间线段最短.
【点睛】本题考查线段的性质:两点之间线段最短.
17.1
【分析】结合实际我们知道,有人胜一局,便有人负一局,那么最后胜局的总数应该等于负数的总局,据此作答即可.
【详解】解:总负局数为 2+3+3=8,
而甲、乙胜局数为4+3=7 ,
故丙胜局数为8-7=1.
故答案为1.
【点睛】本题考查有理数的混合运算,解题的关键是掌握有理数的混合运算法则.
18.(1))①64,63 ; ②25,24 ; ③4.41,3.41;(2)404495;(3),见解析.
【分析】(1)根据一般数据的计算进行解答即可;
(2)从(1)中找出规律,的值比的值相差1即可;
(3)从(1)和(2)中得出规律:.
【详解】解:(1)①64 63 ②25 24 ③4.41 3.41;
(2)已知,那么404495;
(3)从以上过程中,发现的规律是:.
理由如下:
根据平方差公式,得 .
【点睛】本题考查平方差公式,解题的关键是找出其中的规律进行解答.
19.见解析
【分析】先写出已知,求证,画出图形,再证明,即可.
【详解】已知:如图,是的平分线,点P为上任意一点,且,垂足分别为E,F.
求证:.
作图:
证明:∵是的平分线,
∴,
∵,
∴,
在和中,
,
∴,
∴.
【点睛】本题主要考查了全等三角形的判定和性质,解题的关键是证明三角形全等.
20.详见解析.
【详解】试题分析:(1)利用图示:根据平行线的性质,证明“两直线平行,内错角相等”的过程解答;
(2)根据“两直线a∥b,判定同位角∠1=∠3”,然后由对顶角∠3=∠2及等量代换证得
∠1=∠2.
试题解析:
(1)①②;(2)已知:a∥b,直线a、b被直线c所截.
求证:∠1=∠2.
证明:∵a∥b,∴∠1=∠3.
∵∠3 =∠2,∴∠1 =∠2.
21.(1)见解析
(2)见解析
【分析】(1)根据题意画出图形,写出已知和求证即可;
(2)通过角角边证明两个含高的三角形全等,从而得出对应边(高)相等.
【详解】(1)解:已知:如图,中,于点D,于点E.
求证:.
(2)证明:于点D,于点E,
,
,
∴,
∴.
【点睛】本题考查全等三角形在证明三角形两腰上的高相等的应用,掌握角角边的证明方法是本题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
