人教版七年级下册数学课时训练(含解析)第五章第二节平行线——第二课时平行线的判定
文档属性
| 名称 | 人教版七年级下册数学课时训练(含解析)第五章第二节平行线——第二课时平行线的判定 |
|
|
| 格式 | zip | ||
| 文件大小 | 145.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-17 12:53:25 | ||
图片预览

文档简介
平行线第二课时——平行线的判定
一、选择题。
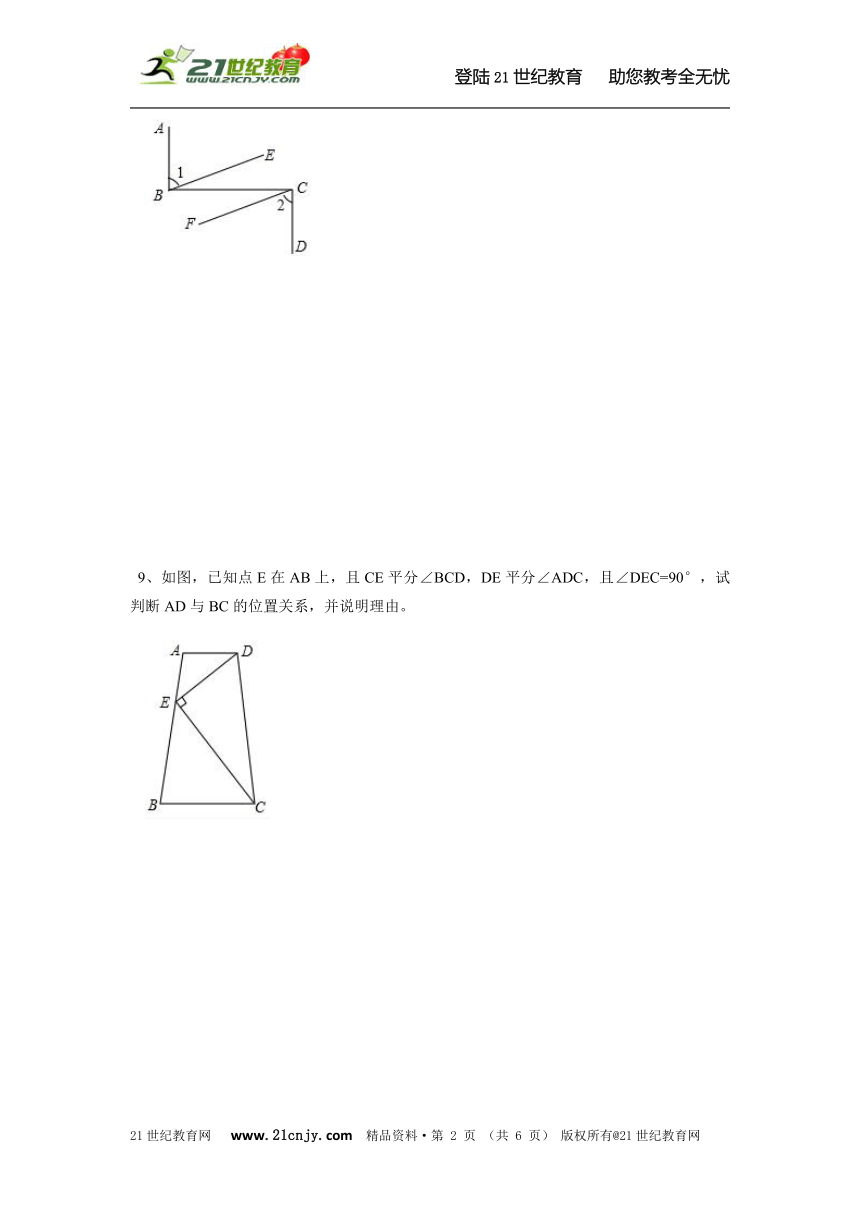
1、下列图形中,由∠1=∠2能得到AB∥CD的是( )
A. B. C. D.
2、如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C. 若∠3=∠2,则b∥c D.若∠3+∠5=180°,则a∥c
3、如图所示,已知∠1=∠2,要使∠3=∠4,只要( )
A.∠1=∠3 B.∠2=∠4 C.∠1=∠4 D.AB∥CD
第2题图 第3题图
二、填空题。
4、如图,直线a、b被直线c所截,若要使a∥b,则需满足的一个条件是_______________(填上你认为适合的一个条件即可)21cnjy.com
5、如图,是小明学习三线八角时制作的模具,经测量∠2=100°,要使木条a与b平行,则∠1的度数必须是________。www.21-cn-jy.com
6、如图一个弯形管道ABCD的拐角∠ABC=120°,∠BCD=60°,这时说管道AB∥CD,依据是______________________________.2·1·c·n·j·y
7、如图,∠A=70°,O是AB 上一点,直线OD与AB所夹的∠BOD=78°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转___________。【来源:21·世纪·教育·网】
第4题图 第5题图 第6题图 第7题图
三、解答题。
8、已知:如图,AB⊥BC,BC⊥CD且∠1=∠2,求证:BE∥CF。
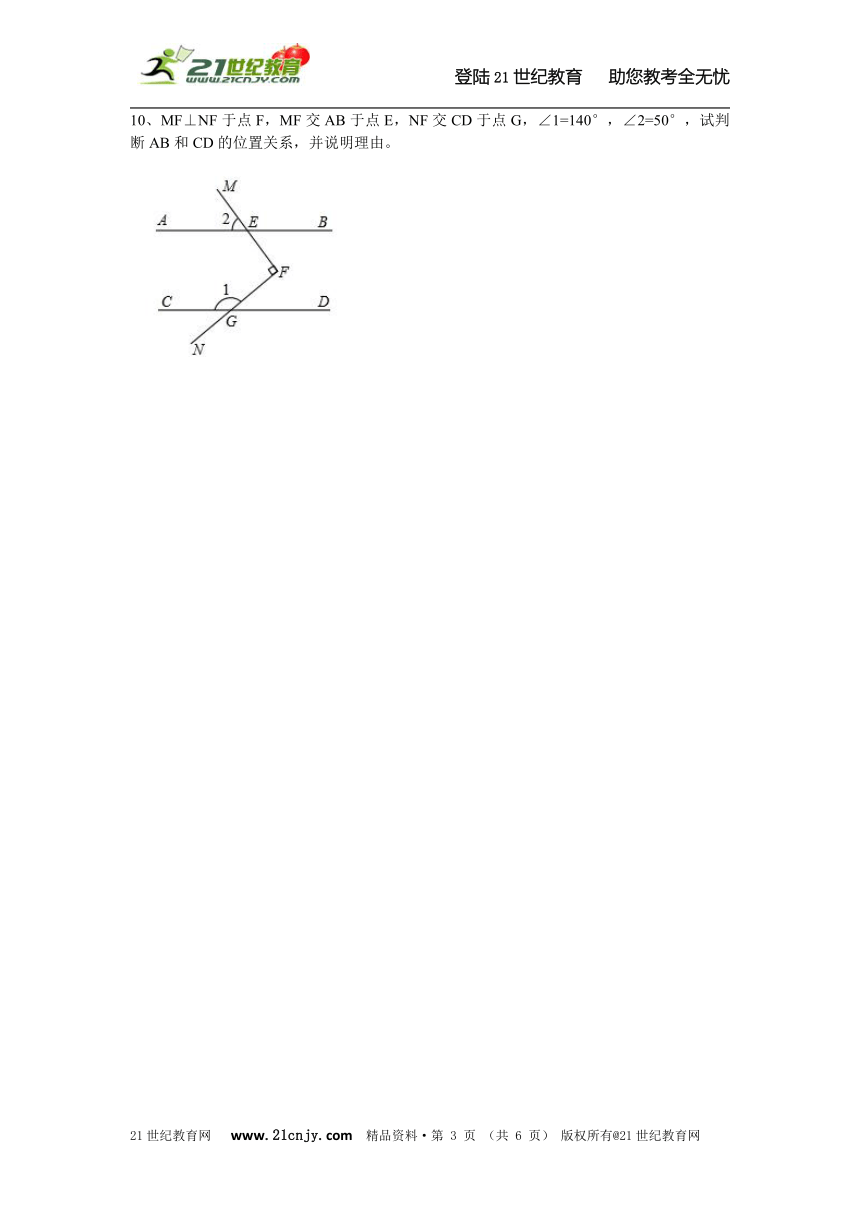
9、如图,已知点E在AB上,且CE平分∠BCD,DE平分∠ADC,且∠DEC=90°,试判断AD与BC的位置关系,并说明理由。21教育网
10、MF⊥NF于点F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由。21·cn·jy·com
参考答案及解析
答案:B。
解析:【解答】A:∠1与∠2是一组同旁内角,同旁内角互补(而不是相等),两直线才平行,故A错误;
B:∠1与∠2是一组内错角,内错角相等,可以判定AB∥CD,故B正确;
C:∠1与∠2是一组内错角,内错角相等,可以判定AC∥BD,而不是AB∥CD,故C错误;
D:∠1与∠2是一组同旁内角,与AB边无关,无法判断AB∥CD,故D错误。
【分析】考查平行线的判定。题意说∠1=∠2,因此只能从同位角、内错角的角度思考。
答案:C。
答案:D
解析:【解答】假设∠3=∠4,又∠1=∠2,那么∠1+∠3=∠2+∠4,即∠CFE=∠BEF。
由内错角相等,两直线平行,可得AB∥CD。
∴当∠1=∠2,要使∠3=∠4,只需要AB∥CD。
【分析】根据平行线的判定,用假设法逆推。
答案:∠1=∠3(或∠1=∠4或∠1+∠2=180°)
解析:【解答】根据“同位角相等,两直线平行”,可得∠1=∠3;
根据“内错角相等,两直线平行”,可得∠1=∠4;
根据“同旁内角互补,两直线平行”,可得∠1+∠2=180°。
【分析】根据平行线的判定:同位角相等、内错角相等、同旁内角互补,两直线平行。
答案:80°。
解析:【解答】如图,∵∠2=100°,∴∠3=∠2=100°(对顶角相等)
∴要使a∥b,则∠1+∠3=180°,
∴∠1=180°-∠3=180°-100°=80°
∴∠1=80°。
【分析】先找出∠2的对顶角,再根据同旁内角互补,两直线平行来解答。
答案:同旁内角互补,两直线平行。
解析:【解答】∠ABC与∠BCD是一组同旁内角,且∠ABC+∠BCD=180°,满足平行线的判定“同旁内角互补,两直线平行”。21世纪教育网版权所有
【分析】根据平行线的判定“同旁内角互补,两直线平行”来判断。
答案:8°。
解析:【解答】要使OD∥AC,则∠BOD=∠A=70°,使得同位角相等,两直线平行。而∠BOD=78°,因此需要绕点O逆时针旋转8°,才会使得∠BOD=70°。
【分析】根据平行线的判定“同位角相等,两直线平行”来判断。
答案:BE∥CF。
解析:【解答】证明:∵AB⊥BC,BC⊥CD
∴∠ABC=∠BCD=90°
∵∠1=∠2
∴∠ABC-∠1=∠BCD-∠2
即∠EBD=∠BCF
∴BE∥CF(内错角相等,两直线平行)
【分析】证明BE∥CF,可通过找内错角来判定。
答案:AD∥BC。
10、答案:AB∥CD。
解析:【解答】
AB∥CD,证明如下:
如图,延长MF交CD于点H。
∵∠1=140°,∴∠FGH=180°-∠1=180°-140°=40°
∵MF⊥NF,∴∠NFH=90°
∴∠FHG=180°-∠FGH-∠NFH=180°-40°-90°=50°
∴∠FHG=∠2
∴AB∥CD(同位角相等,两直线平行)
【分析】利用邻补角、三角形内角和以及平行线的判定来解答。
一、选择题。
1、下列图形中,由∠1=∠2能得到AB∥CD的是( )
A. B. C. D.
2、如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C. 若∠3=∠2,则b∥c D.若∠3+∠5=180°,则a∥c
3、如图所示,已知∠1=∠2,要使∠3=∠4,只要( )
A.∠1=∠3 B.∠2=∠4 C.∠1=∠4 D.AB∥CD
第2题图 第3题图
二、填空题。
4、如图,直线a、b被直线c所截,若要使a∥b,则需满足的一个条件是_______________(填上你认为适合的一个条件即可)21cnjy.com
5、如图,是小明学习三线八角时制作的模具,经测量∠2=100°,要使木条a与b平行,则∠1的度数必须是________。www.21-cn-jy.com
6、如图一个弯形管道ABCD的拐角∠ABC=120°,∠BCD=60°,这时说管道AB∥CD,依据是______________________________.2·1·c·n·j·y
7、如图,∠A=70°,O是AB 上一点,直线OD与AB所夹的∠BOD=78°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转___________。【来源:21·世纪·教育·网】
第4题图 第5题图 第6题图 第7题图
三、解答题。
8、已知:如图,AB⊥BC,BC⊥CD且∠1=∠2,求证:BE∥CF。
9、如图,已知点E在AB上,且CE平分∠BCD,DE平分∠ADC,且∠DEC=90°,试判断AD与BC的位置关系,并说明理由。21教育网
10、MF⊥NF于点F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由。21·cn·jy·com
参考答案及解析
答案:B。
解析:【解答】A:∠1与∠2是一组同旁内角,同旁内角互补(而不是相等),两直线才平行,故A错误;
B:∠1与∠2是一组内错角,内错角相等,可以判定AB∥CD,故B正确;
C:∠1与∠2是一组内错角,内错角相等,可以判定AC∥BD,而不是AB∥CD,故C错误;
D:∠1与∠2是一组同旁内角,与AB边无关,无法判断AB∥CD,故D错误。
【分析】考查平行线的判定。题意说∠1=∠2,因此只能从同位角、内错角的角度思考。
答案:C。
答案:D
解析:【解答】假设∠3=∠4,又∠1=∠2,那么∠1+∠3=∠2+∠4,即∠CFE=∠BEF。
由内错角相等,两直线平行,可得AB∥CD。
∴当∠1=∠2,要使∠3=∠4,只需要AB∥CD。
【分析】根据平行线的判定,用假设法逆推。
答案:∠1=∠3(或∠1=∠4或∠1+∠2=180°)
解析:【解答】根据“同位角相等,两直线平行”,可得∠1=∠3;
根据“内错角相等,两直线平行”,可得∠1=∠4;
根据“同旁内角互补,两直线平行”,可得∠1+∠2=180°。
【分析】根据平行线的判定:同位角相等、内错角相等、同旁内角互补,两直线平行。
答案:80°。
解析:【解答】如图,∵∠2=100°,∴∠3=∠2=100°(对顶角相等)
∴要使a∥b,则∠1+∠3=180°,
∴∠1=180°-∠3=180°-100°=80°
∴∠1=80°。
【分析】先找出∠2的对顶角,再根据同旁内角互补,两直线平行来解答。
答案:同旁内角互补,两直线平行。
解析:【解答】∠ABC与∠BCD是一组同旁内角,且∠ABC+∠BCD=180°,满足平行线的判定“同旁内角互补,两直线平行”。21世纪教育网版权所有
【分析】根据平行线的判定“同旁内角互补,两直线平行”来判断。
答案:8°。
解析:【解答】要使OD∥AC,则∠BOD=∠A=70°,使得同位角相等,两直线平行。而∠BOD=78°,因此需要绕点O逆时针旋转8°,才会使得∠BOD=70°。
【分析】根据平行线的判定“同位角相等,两直线平行”来判断。
答案:BE∥CF。
解析:【解答】证明:∵AB⊥BC,BC⊥CD
∴∠ABC=∠BCD=90°
∵∠1=∠2
∴∠ABC-∠1=∠BCD-∠2
即∠EBD=∠BCF
∴BE∥CF(内错角相等,两直线平行)
【分析】证明BE∥CF,可通过找内错角来判定。
答案:AD∥BC。
10、答案:AB∥CD。
解析:【解答】
AB∥CD,证明如下:
如图,延长MF交CD于点H。
∵∠1=140°,∴∠FGH=180°-∠1=180°-140°=40°
∵MF⊥NF,∴∠NFH=90°
∴∠FHG=180°-∠FGH-∠NFH=180°-40°-90°=50°
∴∠FHG=∠2
∴AB∥CD(同位角相等,两直线平行)
【分析】利用邻补角、三角形内角和以及平行线的判定来解答。
