安徽省蒙城县双涧中学沪科版七年级数学下册课件:8.2 整式乘法(单项式除以单项式)(共13张PPT)
文档属性
| 名称 | 安徽省蒙城县双涧中学沪科版七年级数学下册课件:8.2 整式乘法(单项式除以单项式)(共13张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-18 14:30:35 | ||
图片预览





文档简介
课件13张PPT。8.2标题1标题第8章 整式乘除与因式分解8.2 整式除法回顾与思考(a ≠ 0)1、用字母表示幂的运算性质:1(3) (a2)3 ·(-a3 )÷(a3)5 (4) (x4)6 ÷(x6)2 ·(-x4 )2= a10= an=?a9 ÷a15=?a?6=?=x24÷x12 ·x8=x 24 —12+8=x20答: 月球距离地球大约 3.84×105千米, 一架飞机的速度约为 8×102 千米/时. 如果乘坐此飞机飞行这么远的距离, 大约需要多少时间 ? 3.84×105 ÷( 8×102 )?这样列式的依据= 0.48×103 ?如何得到的?单位是什么=480(小时) ?如何得到的=20(天) .?做完了吗如果乘坐此飞机飞行这么远的距离, 大约需要20天时间. 你能直接列出一个时间为天的算式吗?3.84×105÷( 8×102 )÷24.你会计算吗?类 比 探 索计算下列各题, 并说说你的理由:
(1) (x5y) ÷x2 ;
(2) (14a3b2x) ÷(2ab2) ;
(3) (a4b2c)÷(2a2b) . 解:(1) (x5y) ÷x2 把除法式子写成分数形式,= 把幂写成乘积形式, 约分。== x·x·x·y= x3y 省略分数及其运算, 上述过程相当于: (1)(x5y) ÷x2
=(x5÷x2 )·y
=x 5 ? 2 ·y(2) (14a3b2x) ÷(2ab2)
==(14÷2)·a 3 ? 1·b2? 2 ·x(3)(14÷2 )·(a3÷a)·(b2÷b2)·x探 索 (1)(x5y) ÷x2
=(x5÷x2 )·y
=x 5 ? 2 ·y=7a2x=?a2bc观察、归纳(1) (x5y) ÷ x2 = x5 ? 2 ·y
(2) (14a3b2x) ÷ (2ab2) = (14÷2 )·a3 ? 1·b2 ? 2 ·x ;
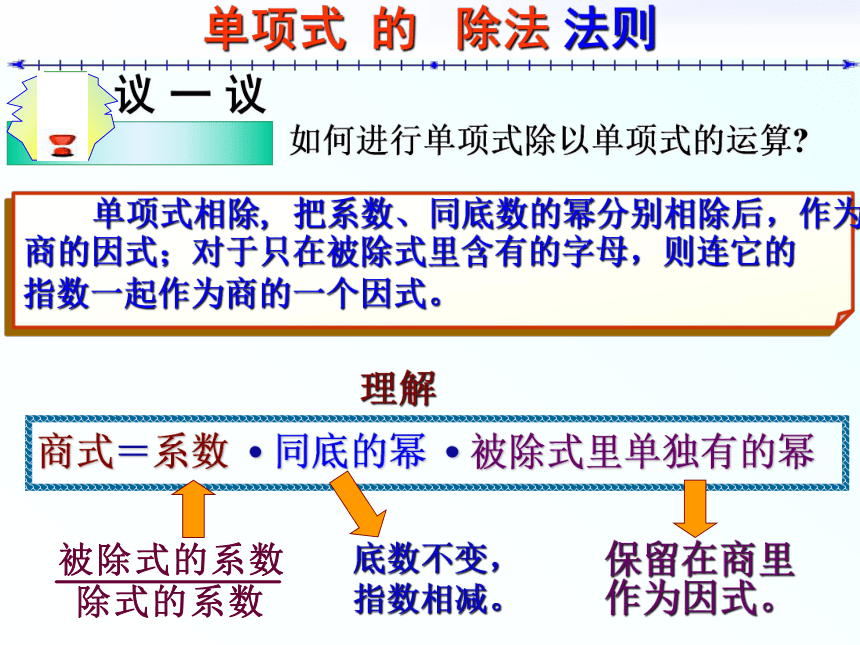
(3) (a4b2c) ÷ (2a2b) = (1÷2 )·a4 ? 2·b2 ?1·c .商式被除式除式 仔细观察一下,并分析与思考下列几点:(被除式的系数)÷ (除式的系数)写在商里面作(被除式的指数) —(除式的指数)商式的系数=单项式除以单项式,其结果(商式)仍是被除式里单独有的幂,(同底数幂) 商的指数=一个单项式;?因式。单项式 的 除法 法则如何进行单项式除以单项式的运算? 单项式相除, 把系数、同底数的幂分别相除后,作为
商的因式;对于只在被除式里含有的字母,则连它的
指数一起作为商的一个因式。 底数不变,
指数相减。保留在商里
作为因式。例题解析例题 例1 计算:
(1) ; (2) 2a2b .(-3b2c)÷(4ab3);(3) (2x2y)3·(?7xy2)÷(14x4y3); (4) (2a+b)4÷(2a+b)2.三块之间是同级运
算, 一般从左到右,不然容易出错。随堂练习p143 (1) (10ab3)÷(5b2) ; (2) (-14s2)÷(8s) ;
(3) (3a5b3c)÷(-12a2b) ; (4) (2x2y)3÷(6x3y2) .(-2xy)1、计算:接综合练习观察、归纳(1) (625+125+50)÷25 =( )+( )+( )
(2) (4a+6)÷2=( )÷2 +( )÷2=( )
(2a2-a)÷(-2a) =( )÷(-2a) + ( )÷(-2a) =( )仔细观察一下,你能归纳多项式除以单项式的运算方法: 把这个多项式的每一项除以这个单项式 多项式除以单项式,其结果(商式)仍(a+b+c) ÷m= 再把所得的商相加一个多项式;?a ÷ m + b ÷ m + c ÷ m 。先填空:再用适当的方法验证计算的正确性例题解析例题 例2计算:
( 14a3-7a2)÷(7a);
(2) (15x3y 5?10x4y4 ?20x3y2)÷(-5x3y2)多项式的每一项要包前面的符号随堂练习p143 (1) (15x2y –10xy2)÷(5xy) ;
(2) (4s3t2 –6s2t3)÷(- 3s2t) ;
(3) (5x3 – 2x2 + 6x)÷(3x) ;
2、计算:接综合练习巩固练 习1、计算填空:⑴ (60x3y5) ÷(?12xy3) = ;综(2) (8x6y4z) ÷( ) =?4x2y2 ;(3) ( )÷(2x3y3 ) = ;合(4) 若 (ax3my12)÷(3x3y2n)=4x6y8 ,
则 a = , m = ,n = ;2、能力挑战:?5x2y2?2x4y2z1232本节课你的收获是什么?小结本节课你学到了什么? 在计算题时,要注意运算顺序和符号. 同底数幂相除是整式除法的特例; 单项式除以单项式的法则;多项式除以单项式的法则的探求过程中我们使用了观察、归纳的方法,这是数学发现规律的一种常用方法。
(1) (x5y) ÷x2 ;
(2) (14a3b2x) ÷(2ab2) ;
(3) (a4b2c)÷(2a2b) . 解:(1) (x5y) ÷x2 把除法式子写成分数形式,= 把幂写成乘积形式, 约分。== x·x·x·y= x3y 省略分数及其运算, 上述过程相当于: (1)(x5y) ÷x2
=(x5÷x2 )·y
=x 5 ? 2 ·y(2) (14a3b2x) ÷(2ab2)
==(14÷2)·a 3 ? 1·b2? 2 ·x(3)(14÷2 )·(a3÷a)·(b2÷b2)·x探 索 (1)(x5y) ÷x2
=(x5÷x2 )·y
=x 5 ? 2 ·y=7a2x=?a2bc观察、归纳(1) (x5y) ÷ x2 = x5 ? 2 ·y
(2) (14a3b2x) ÷ (2ab2) = (14÷2 )·a3 ? 1·b2 ? 2 ·x ;
(3) (a4b2c) ÷ (2a2b) = (1÷2 )·a4 ? 2·b2 ?1·c .商式被除式除式 仔细观察一下,并分析与思考下列几点:(被除式的系数)÷ (除式的系数)写在商里面作(被除式的指数) —(除式的指数)商式的系数=单项式除以单项式,其结果(商式)仍是被除式里单独有的幂,(同底数幂) 商的指数=一个单项式;?因式。单项式 的 除法 法则如何进行单项式除以单项式的运算? 单项式相除, 把系数、同底数的幂分别相除后,作为
商的因式;对于只在被除式里含有的字母,则连它的
指数一起作为商的一个因式。 底数不变,
指数相减。保留在商里
作为因式。例题解析例题 例1 计算:
(1) ; (2) 2a2b .(-3b2c)÷(4ab3);(3) (2x2y)3·(?7xy2)÷(14x4y3); (4) (2a+b)4÷(2a+b)2.三块之间是同级运
算, 一般从左到右,不然容易出错。随堂练习p143 (1) (10ab3)÷(5b2) ; (2) (-14s2)÷(8s) ;
(3) (3a5b3c)÷(-12a2b) ; (4) (2x2y)3÷(6x3y2) .(-2xy)1、计算:接综合练习观察、归纳(1) (625+125+50)÷25 =( )+( )+( )
(2) (4a+6)÷2=( )÷2 +( )÷2=( )
(2a2-a)÷(-2a) =( )÷(-2a) + ( )÷(-2a) =( )仔细观察一下,你能归纳多项式除以单项式的运算方法: 把这个多项式的每一项除以这个单项式 多项式除以单项式,其结果(商式)仍(a+b+c) ÷m= 再把所得的商相加一个多项式;?a ÷ m + b ÷ m + c ÷ m 。先填空:再用适当的方法验证计算的正确性例题解析例题 例2计算:
( 14a3-7a2)÷(7a);
(2) (15x3y 5?10x4y4 ?20x3y2)÷(-5x3y2)多项式的每一项要包前面的符号随堂练习p143 (1) (15x2y –10xy2)÷(5xy) ;
(2) (4s3t2 –6s2t3)÷(- 3s2t) ;
(3) (5x3 – 2x2 + 6x)÷(3x) ;
2、计算:接综合练习巩固练 习1、计算填空:⑴ (60x3y5) ÷(?12xy3) = ;综(2) (8x6y4z) ÷( ) =?4x2y2 ;(3) ( )÷(2x3y3 ) = ;合(4) 若 (ax3my12)÷(3x3y2n)=4x6y8 ,
则 a = , m = ,n = ;2、能力挑战:?5x2y2?2x4y2z1232本节课你的收获是什么?小结本节课你学到了什么? 在计算题时,要注意运算顺序和符号. 同底数幂相除是整式除法的特例; 单项式除以单项式的法则;多项式除以单项式的法则的探求过程中我们使用了观察、归纳的方法,这是数学发现规律的一种常用方法。
