26.2.2 实际问题与反比例函数 课件(共15张PPT)2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 26.2.2 实际问题与反比例函数 课件(共15张PPT)2024-2025学年数学人教版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 780.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-14 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
26.2.2 实际问题与反比例函数
1. 通过对“杠杆原理”等实际问题与反比例函数关系的
探究,使学生体会数学建模思想和学以致用的数学
理念,并能从函数的观点来解决一些实际问题. (重
点)
2. 掌握反比例函数在其他学科中的运用,体验学科的
整合思想. (重点、难点)
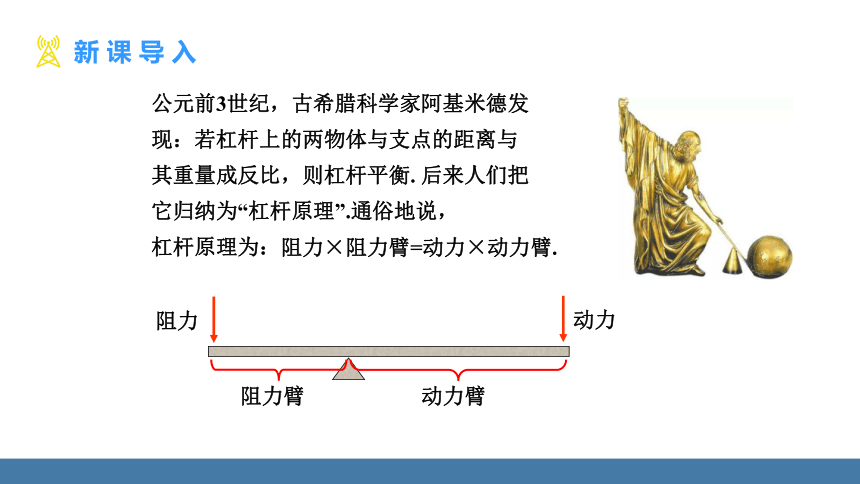
公元前3世纪,古希腊科学家阿基米德发现:若杠杆上的两物体与支点的距离与其重量成反比,则杠杆平衡. 后来人们把它归纳为“杠杆原理”.通俗地说,
杠杆原理为:
阻力×阻力臂=动力×动力臂.
阻力
动力
阻力臂
动力臂
探究1 小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为 1200 N
和 0.5 m.
(1) 动力 F 与动力臂 l 有怎样的函数关系 当动力臂为1.5 m时,撬动
石头至少需要多大的力
解:根据“杠杆原理”,得 Fl =1200×0.5,
∴ F 关于l 的函数解析式为
当 l=1.5 时,
∴撬动石头至少需要400 N的力.
(2) 若想使动力 F 不超过题 (1) 中所用力的一半,则动力臂l至少要
加长多少
点拨: 对于函数 ,F 随 l 的增大而减小.
因此,只要求出 F =200 N 时对应的 l 的值,就能
确定动力臂 l 至少应加长的量
解:当F=400× =200 时,由200 = ,得
3-1.5 =1.5 (m).
∴动力臂至少要加长 1.5 m.
想一想:1.什么是“杠杆定律”?已知阻力与阻力臂不变,设动力为F,动力臂为L,当F变大时,L怎么变?当F变小时,L又怎么变?
2.在第(2)问中,根据第(1)问的答案,可得F≤200,要求出动力臂至少要加长多少,就是要求L的什么值?由此判断我们在使用撬棍时,为什么动力臂越长就越省力?
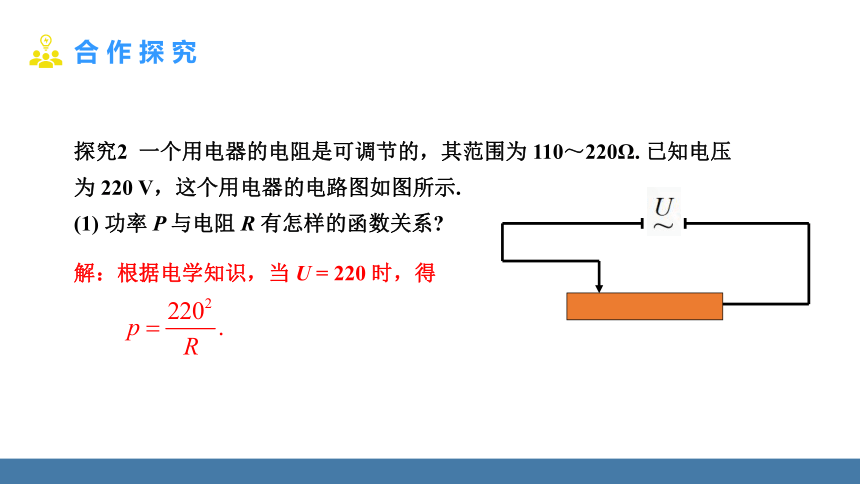
探究2 一个用电器的电阻是可调节的,其范围为 110~220Ω. 已知电压为 220 V,这个用电器的电路图如图所示.
(1) 功率 P 与电阻 R 有怎样的函数关系
解:根据电学知识,当 U = 220 时,得
(2) 这个用电器功率的范围是多少
解:根据反比例函数的性质可知,电阻越大,功率越小.
把电阻的最小值 R = 110 代入求得的解析式,
得到功率的最大值
把电阻的最大值 R = 220 代入求得的解析式,
得到功率的最小值
因此用电器功率的范围为220~440 W.
想一想:当用电器两端的电压一定时,用电器的输出功率与它的电阻之间呈什么关系?这一特征说明用电器的输出功率与它的电阻之间满足什么函数关系?
归纳: 解答问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
其中往往要用到电学中的公式PR=U2,P指用电器的输出功率(瓦),U 指用电器两端的电压(伏),R指用电器的电阻(欧姆).
例1 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压 p (kPa) 是气体体积 V (m3)的反比例函数,其图象如图所示,当气球内的气压大于120 kPa 时,气球将爆炸.为了安全起见,气球的体积应 ( )
A. 不大于 B. 小于
C. 不小于 D. 大于
C
O
60
V/m3
p/kPa
1.6
例2 当电压为 220 V 时 (电压=电流×电阻),通过电路的电流 I (A)
与电路中的电阻 R (Ω) 之间的函数关系为 ( )
B. I=220R
D. R=220I
A.
C.
A
1.某物体对地面的压力为定值,物体对地面的压强 与受力面积
之间的函数关系如图所示,则这一函数关系式为_ ________.
2. 在一个可以改变体积的密闭容器内装有一定质量的
二氧化碳,当改变容器的体积时,气体的密度也会
随之改变,密度ρ (单位:kg/m3) 是体积 V (单位:
m3) 的反比例函数,它的图象如图所示,
当 V =10 m3 时,气体的
密度是 .
2
1
3
4
5
V/m3
ρ/(kg/m3)
5
O
6
3
2
4
1
1 kg/m3
3.已知蓄电池的电压为定值,使用蓄电池时,电流 I (单位:A)与电阻 R (单位:Ω)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的用电器的限制电流不能超过 6 A,那么用电器的可变电阻 R 应控制在( )
A.R≥2 Ω B.0 Ω<R≤2 Ω
C.R≥1 Ω D.0 Ω<R≤1 Ω
I/A
R/Ω
2
3
O
C
反比例函数在其他学科中的应用
与力学的综合
与电学的综合
、杠杆原理
,
建模
26.2.2 实际问题与反比例函数
1. 通过对“杠杆原理”等实际问题与反比例函数关系的
探究,使学生体会数学建模思想和学以致用的数学
理念,并能从函数的观点来解决一些实际问题. (重
点)
2. 掌握反比例函数在其他学科中的运用,体验学科的
整合思想. (重点、难点)
公元前3世纪,古希腊科学家阿基米德发现:若杠杆上的两物体与支点的距离与其重量成反比,则杠杆平衡. 后来人们把它归纳为“杠杆原理”.通俗地说,
杠杆原理为:
阻力×阻力臂=动力×动力臂.
阻力
动力
阻力臂
动力臂
探究1 小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为 1200 N
和 0.5 m.
(1) 动力 F 与动力臂 l 有怎样的函数关系 当动力臂为1.5 m时,撬动
石头至少需要多大的力
解:根据“杠杆原理”,得 Fl =1200×0.5,
∴ F 关于l 的函数解析式为
当 l=1.5 时,
∴撬动石头至少需要400 N的力.
(2) 若想使动力 F 不超过题 (1) 中所用力的一半,则动力臂l至少要
加长多少
点拨: 对于函数 ,F 随 l 的增大而减小.
因此,只要求出 F =200 N 时对应的 l 的值,就能
确定动力臂 l 至少应加长的量
解:当F=400× =200 时,由200 = ,得
3-1.5 =1.5 (m).
∴动力臂至少要加长 1.5 m.
想一想:1.什么是“杠杆定律”?已知阻力与阻力臂不变,设动力为F,动力臂为L,当F变大时,L怎么变?当F变小时,L又怎么变?
2.在第(2)问中,根据第(1)问的答案,可得F≤200,要求出动力臂至少要加长多少,就是要求L的什么值?由此判断我们在使用撬棍时,为什么动力臂越长就越省力?
探究2 一个用电器的电阻是可调节的,其范围为 110~220Ω. 已知电压为 220 V,这个用电器的电路图如图所示.
(1) 功率 P 与电阻 R 有怎样的函数关系
解:根据电学知识,当 U = 220 时,得
(2) 这个用电器功率的范围是多少
解:根据反比例函数的性质可知,电阻越大,功率越小.
把电阻的最小值 R = 110 代入求得的解析式,
得到功率的最大值
把电阻的最大值 R = 220 代入求得的解析式,
得到功率的最小值
因此用电器功率的范围为220~440 W.
想一想:当用电器两端的电压一定时,用电器的输出功率与它的电阻之间呈什么关系?这一特征说明用电器的输出功率与它的电阻之间满足什么函数关系?
归纳: 解答问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
其中往往要用到电学中的公式PR=U2,P指用电器的输出功率(瓦),U 指用电器两端的电压(伏),R指用电器的电阻(欧姆).
例1 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压 p (kPa) 是气体体积 V (m3)的反比例函数,其图象如图所示,当气球内的气压大于120 kPa 时,气球将爆炸.为了安全起见,气球的体积应 ( )
A. 不大于 B. 小于
C. 不小于 D. 大于
C
O
60
V/m3
p/kPa
1.6
例2 当电压为 220 V 时 (电压=电流×电阻),通过电路的电流 I (A)
与电路中的电阻 R (Ω) 之间的函数关系为 ( )
B. I=220R
D. R=220I
A.
C.
A
1.某物体对地面的压力为定值,物体对地面的压强 与受力面积
之间的函数关系如图所示,则这一函数关系式为_ ________.
2. 在一个可以改变体积的密闭容器内装有一定质量的
二氧化碳,当改变容器的体积时,气体的密度也会
随之改变,密度ρ (单位:kg/m3) 是体积 V (单位:
m3) 的反比例函数,它的图象如图所示,
当 V =10 m3 时,气体的
密度是 .
2
1
3
4
5
V/m3
ρ/(kg/m3)
5
O
6
3
2
4
1
1 kg/m3
3.已知蓄电池的电压为定值,使用蓄电池时,电流 I (单位:A)与电阻 R (单位:Ω)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的用电器的限制电流不能超过 6 A,那么用电器的可变电阻 R 应控制在( )
A.R≥2 Ω B.0 Ω<R≤2 Ω
C.R≥1 Ω D.0 Ω<R≤1 Ω
I/A
R/Ω
2
3
O
C
反比例函数在其他学科中的应用
与力学的综合
与电学的综合
、杠杆原理
,
建模
