27.2.1.1 平行线分线段成比例 课件(共21张PPT) 2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 27.2.1.1 平行线分线段成比例 课件(共21张PPT) 2024-2025学年数学人教版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-15 21:48:36 | ||
图片预览





文档简介
(共21张PPT)
27.2.1 相似三角形的判定
第1课时 平行线分线段成比例
1. 能用符号表示两个三角形相似,能确定它们的相似比、对应边和对应角.
2. 能叙述平行线分线段成比例定理及其推论,并能结合图形写出正确的比例式.
3. 能用平行线分线段成比例定理的推论证明三角形相似的判定定理.
在相似多边形中,最简单的就是相似三角形.
∠A=∠A',∠B=∠B',∠C=∠C',
在△ABC和△A'B'C'中,如果
我们就说△ABC和△A'B'C'相似,相似比为k,相似用符号“∽”表示,读作“相似于”.△ABC 和△A'B'C'相似记作△ABC∽△A'B'C'.
即三个角分别相等,三条边成比例,
想一想: 判定两个三角形全等时,除了可以验证它们所有的角和边分别相等外,还可以使用简便的判定方法(SSS,SAS,ASA,AAS).类似地,判定两个三角形相似时,是不是也存在简便的判定方法呢?我们先来探究下面的问题.
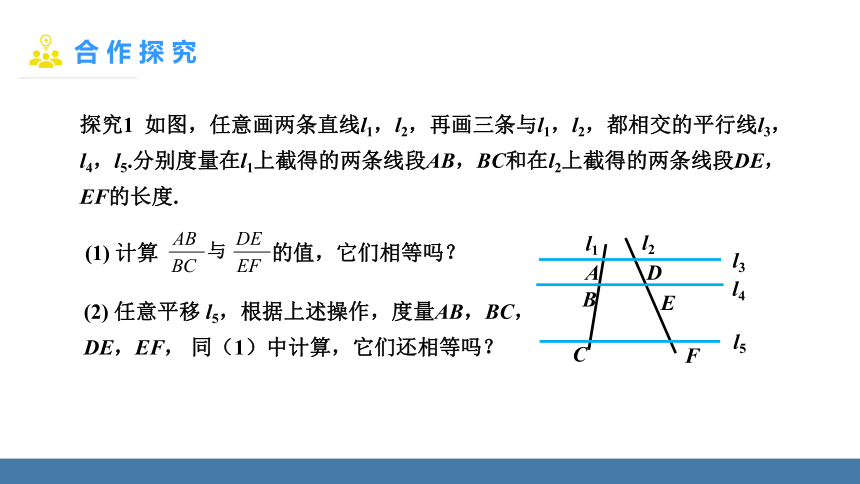
探究1 如图,任意画两条直线l1,l2,再画三条与l1,l2,都相交的平行线l3,l4,l5.分别度量在l1上截得的两条线段AB,BC和在l2上截得的两条线段DE,EF的长度.
A
C
E
B
D
F
l4
l5
l1
l2
l3
(1) 计算 的值,它们相等吗?
(2) 任意平移 l5,根据上述操作,度量AB,BC,DE,EF, 同(1)中计算,它们还相等吗?
A
C
E
B
D
F
l4
l5
l1
l2
l3
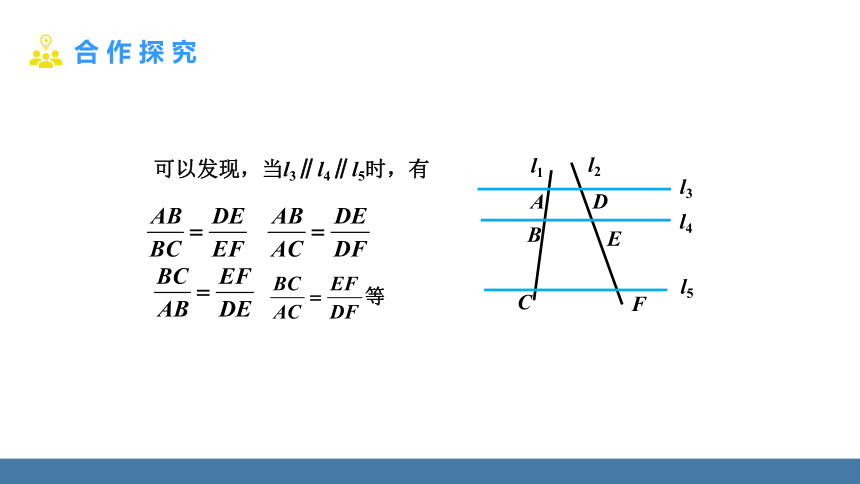
可以发现,当l3∥l4∥l5时,有
归纳:一般地,我们有平行线分线段成比例的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
A
B
C
D
E
F
l4
l5
l3
l2
l1
符号语言:
若l3∥l4∥ l5,
则 , ,
,
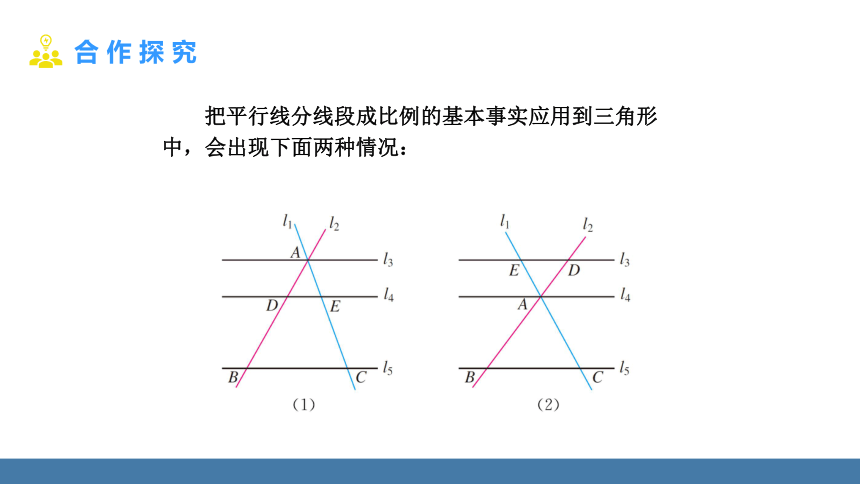
把平行线分线段成比例的基本事实应用到三角形中,会出现下面两种情况:
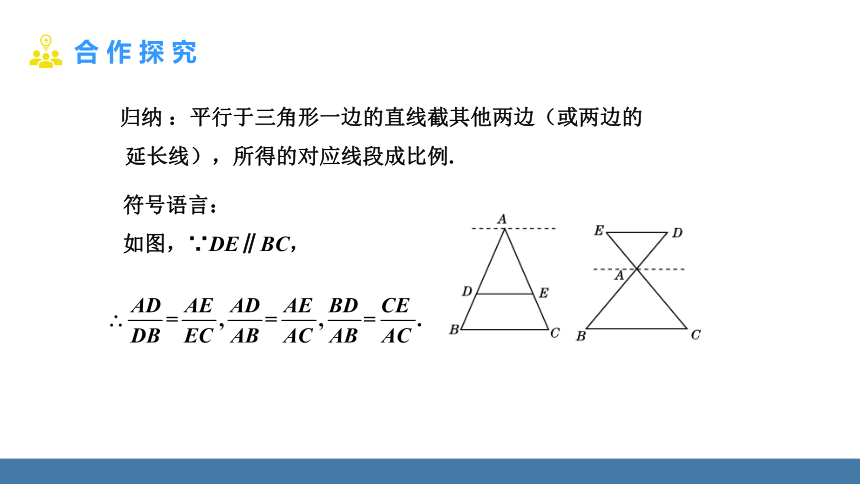
归纳 :平行于三角形一边的直线截其他两边(或两边的
延长线),所得的对应线段成比例.
符号语言:
如图,∵DE∥BC,
例1 如图, , , , ,
则 _ _______.
探究2 如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.
问题1 △ADE与△ABC的三个内角分别相等吗?
问题2 分别度量△ADE与△ABC的边长,它们的边长是否对应成比例?
B
C
A
D
E
问题3 你认为△ADE与△ABC之间有什么关系?平行移动DE的位置,你的结论还成立吗?
B
C
A
D
E
通过度量,我们发现△ADE∽△ABC,
且只要DE∥BC,这个结论恒成立.
B
C
A
D
E
想一想: 我们通过度量三角形的边长,知道△ADE∽△ABC,
但要用相似的定义去证明它,我们需要证明什么?
由前面的结论,我们可以得到什么?还需证明什么?
证明:在 △ADE与 △ABC中,∠A=∠A.
∵ DE∥BC,
∴ ∠ADE=∠B,∠AED=∠C.
如图,过点 E 作 EF∥AB,交 BC 于点 F.
C
A
B
D
E
F
用相似的定义证明△ADE∽△ABC
∵ DE∥BC,EF∥AB,
∴
C
A
B
D
E
F
∵ 四边形DEFB为平行四边形,
∴ DE=BF.
∴△ADE∽△ABC.
∴
归纳:由此我们得到判定三角形相似的定理:
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.
三角形相似的两种常见类型:
“A ”型
“X ”型
D
E
A
B
C
A
B
C
D
E
例2 如图,在 中,若 , , ,
则 的长是_____.
10
例3 如图,AB//EF//DC,AD//BC,EF 与 AC 交于点 G,则图中的
相似三角形共有( )
A.3对 B.5对
C.6对 D.8对
C
D
A
B
E
F
G
C
点拨 : △AEG∽
△ADC∽ △CFG ∽△CBA.
△AEG ∽△ADC,△AEG ∽ △CFG,
△AEG ∽△CBA,△ADC∽△CFG,
△ADC ∽△CBA,△CFG∽△CBA.
1.如图,在 △ABC 中,EF∥BC,AE = 2 cm,BE = 6 cm,
BC = 4 cm,则 EF 的长为 ( )
A
A
B
C
E
F
A. 1 cm B. cm
C. 2 cm D. 3 cm
2.如图所示,如果D,E,F分别在OA,OB,OC上,且DF∥AC,EF∥BC.
求证:OD∶OA=OE∶OB
证明: ∵ DF∥AC,
∵ EF∥BC,
两条直线被一组平行线所截,所得的对应线段成比例
推论
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例
判定三角形相似的定理
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似
基本事实
平行线分线段成比例
27.2.1 相似三角形的判定
第1课时 平行线分线段成比例
1. 能用符号表示两个三角形相似,能确定它们的相似比、对应边和对应角.
2. 能叙述平行线分线段成比例定理及其推论,并能结合图形写出正确的比例式.
3. 能用平行线分线段成比例定理的推论证明三角形相似的判定定理.
在相似多边形中,最简单的就是相似三角形.
∠A=∠A',∠B=∠B',∠C=∠C',
在△ABC和△A'B'C'中,如果
我们就说△ABC和△A'B'C'相似,相似比为k,相似用符号“∽”表示,读作“相似于”.△ABC 和△A'B'C'相似记作△ABC∽△A'B'C'.
即三个角分别相等,三条边成比例,
想一想: 判定两个三角形全等时,除了可以验证它们所有的角和边分别相等外,还可以使用简便的判定方法(SSS,SAS,ASA,AAS).类似地,判定两个三角形相似时,是不是也存在简便的判定方法呢?我们先来探究下面的问题.
探究1 如图,任意画两条直线l1,l2,再画三条与l1,l2,都相交的平行线l3,l4,l5.分别度量在l1上截得的两条线段AB,BC和在l2上截得的两条线段DE,EF的长度.
A
C
E
B
D
F
l4
l5
l1
l2
l3
(1) 计算 的值,它们相等吗?
(2) 任意平移 l5,根据上述操作,度量AB,BC,DE,EF, 同(1)中计算,它们还相等吗?
A
C
E
B
D
F
l4
l5
l1
l2
l3
可以发现,当l3∥l4∥l5时,有
归纳:一般地,我们有平行线分线段成比例的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
A
B
C
D
E
F
l4
l5
l3
l2
l1
符号语言:
若l3∥l4∥ l5,
则 , ,
,
把平行线分线段成比例的基本事实应用到三角形中,会出现下面两种情况:
归纳 :平行于三角形一边的直线截其他两边(或两边的
延长线),所得的对应线段成比例.
符号语言:
如图,∵DE∥BC,
例1 如图, , , , ,
则 _ _______.
探究2 如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.
问题1 △ADE与△ABC的三个内角分别相等吗?
问题2 分别度量△ADE与△ABC的边长,它们的边长是否对应成比例?
B
C
A
D
E
问题3 你认为△ADE与△ABC之间有什么关系?平行移动DE的位置,你的结论还成立吗?
B
C
A
D
E
通过度量,我们发现△ADE∽△ABC,
且只要DE∥BC,这个结论恒成立.
B
C
A
D
E
想一想: 我们通过度量三角形的边长,知道△ADE∽△ABC,
但要用相似的定义去证明它,我们需要证明什么?
由前面的结论,我们可以得到什么?还需证明什么?
证明:在 △ADE与 △ABC中,∠A=∠A.
∵ DE∥BC,
∴ ∠ADE=∠B,∠AED=∠C.
如图,过点 E 作 EF∥AB,交 BC 于点 F.
C
A
B
D
E
F
用相似的定义证明△ADE∽△ABC
∵ DE∥BC,EF∥AB,
∴
C
A
B
D
E
F
∵ 四边形DEFB为平行四边形,
∴ DE=BF.
∴△ADE∽△ABC.
∴
归纳:由此我们得到判定三角形相似的定理:
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.
三角形相似的两种常见类型:
“A ”型
“X ”型
D
E
A
B
C
A
B
C
D
E
例2 如图,在 中,若 , , ,
则 的长是_____.
10
例3 如图,AB//EF//DC,AD//BC,EF 与 AC 交于点 G,则图中的
相似三角形共有( )
A.3对 B.5对
C.6对 D.8对
C
D
A
B
E
F
G
C
点拨 : △AEG∽
△ADC∽ △CFG ∽△CBA.
△AEG ∽△ADC,△AEG ∽ △CFG,
△AEG ∽△CBA,△ADC∽△CFG,
△ADC ∽△CBA,△CFG∽△CBA.
1.如图,在 △ABC 中,EF∥BC,AE = 2 cm,BE = 6 cm,
BC = 4 cm,则 EF 的长为 ( )
A
A
B
C
E
F
A. 1 cm B. cm
C. 2 cm D. 3 cm
2.如图所示,如果D,E,F分别在OA,OB,OC上,且DF∥AC,EF∥BC.
求证:OD∶OA=OE∶OB
证明: ∵ DF∥AC,
∵ EF∥BC,
两条直线被一组平行线所截,所得的对应线段成比例
推论
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例
判定三角形相似的定理
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似
基本事实
平行线分线段成比例
