27.2.1.2 相似三角形的判定定理1,2 课件(共21张PPT) 2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 27.2.1.2 相似三角形的判定定理1,2 课件(共21张PPT) 2024-2025学年数学人教版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-15 00:00:00 | ||
图片预览



文档简介
(共21张PPT)
27.2.1 相似三角形的判定
第2课时 相似三角形的判定定理1,2
1.探索用三边关系判定三角形相似定理
2.掌握利用三边来判定两个三角形相似的方法,并能进行相关计算. (重点、难点)
3.探索“两边成比例且夹角相等的两个三角形相似”的判定定理.
4.会根据边和角的关系来判定两个三角形相似,并进行相关计算. (重点、难点)
思考:学习三角形全等时,我们知道有判定两个三角形的简便方法(SSS、SAS、ASA、AAS).
类似于判定三角形全等 的SSS方法,我们能不能通过三边来判断两 个三角形相似呢?
回顾:上节课我们探究了平行线分线段成比例定理
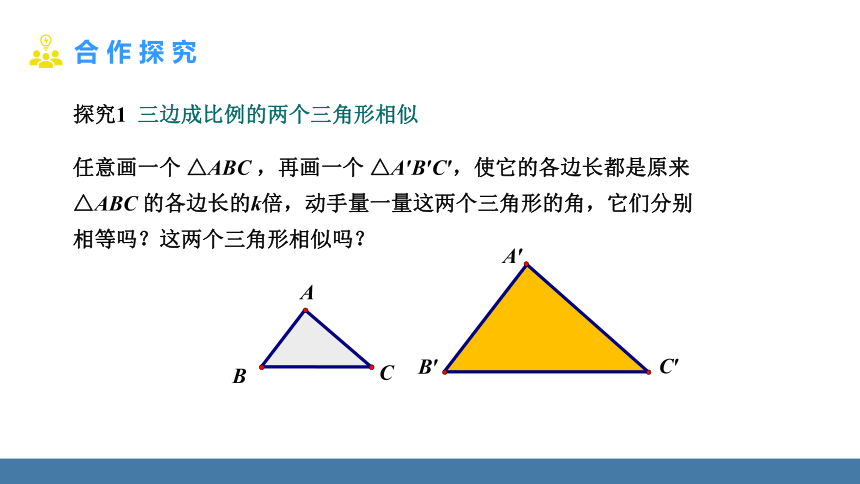
任意画一个 △ABC ,再画一个 △A′B′C′,使它的各边长都是原来
△ABC 的各边长的k倍,动手量一量这两个三角形的角,它们分别
相等吗?这两个三角形相似吗?
A′
B′
C′
C
B
A
探究1 三边成比例的两个三角形相似
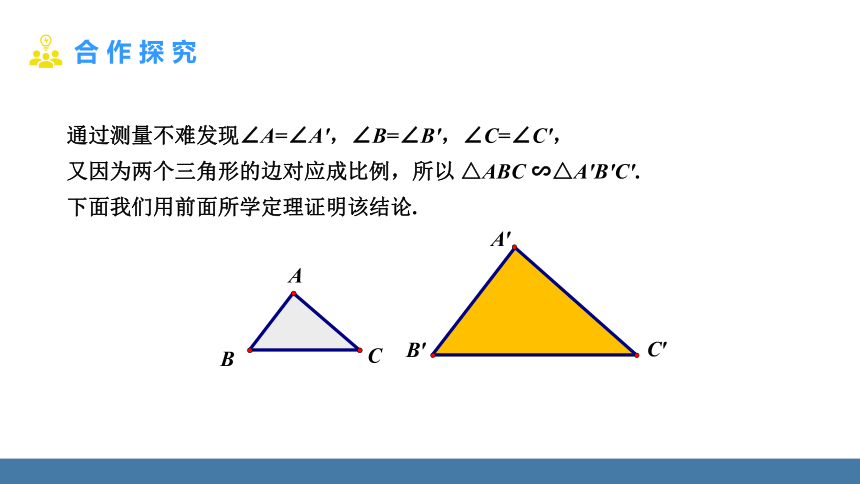
通过测量不难发现∠A=∠A',∠B=∠B',∠C=∠C',
又因为两个三角形的边对应成比例,所以 △ABC ∽△A′B′C′.
下面我们用前面所学定理证明该结论.
A′
B′
C′
C
B
A
∴
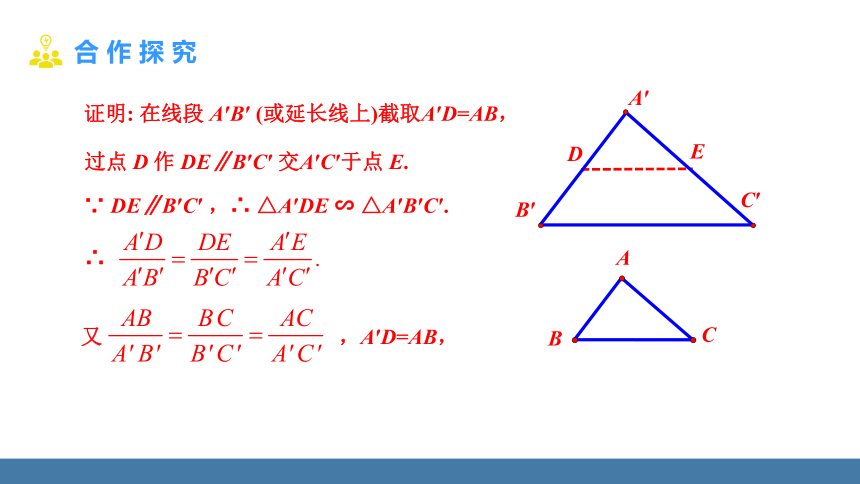
证明: 在线段 A′B′ (或延长线上)截取A′D=AB,
过点 D 作 DE∥B′C′ 交A′C′于点 E.
∵ DE∥B′C′ ,∴ △A′DE ∽ △A′B′C′.
又 ,A′D=AB,
C
B
A
B′
C′
A′
D
E
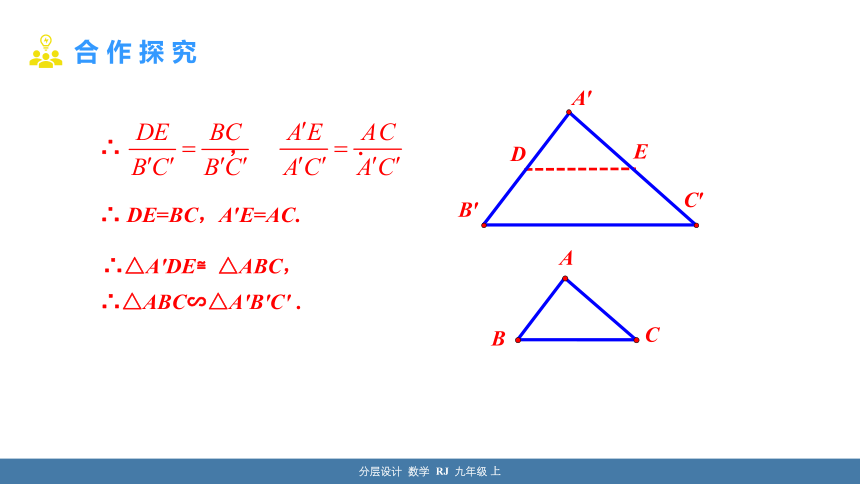
∴ DE=BC,A′E=AC.
∴△A′DE≌△ABC,
∴△ABC∽△A′B′C′ .
∴ , .
C
B
A
B′
C′
A′
D
E
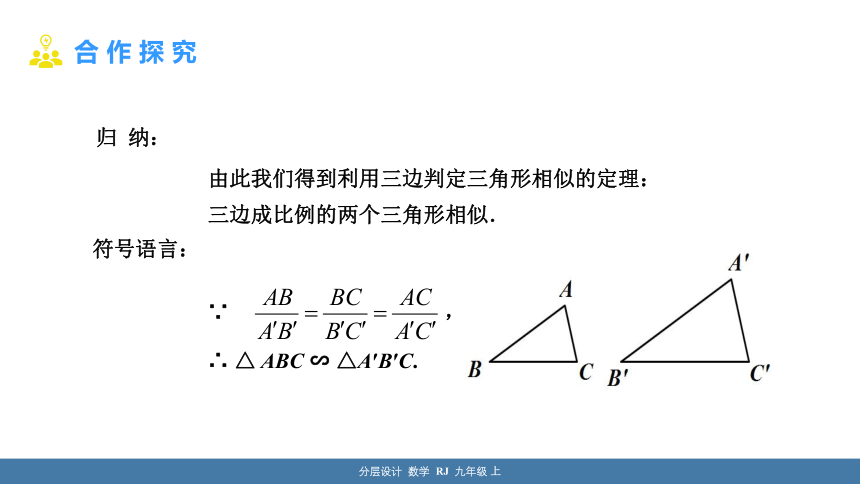
由此我们得到利用三边判定三角形相似的定理:
三边成比例的两个三角形相似.
归 纳:
符号语言:
∵ ,
∴ △ ABC ∽ △A′B′C.
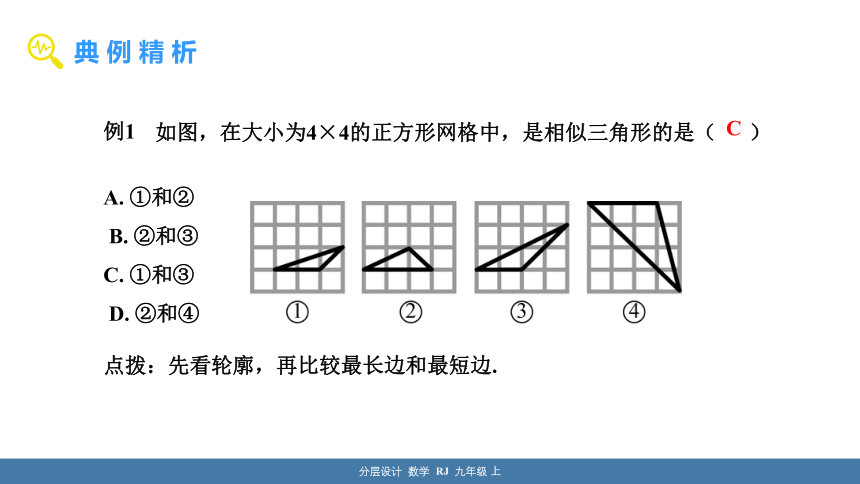
例1
如图,在大小为4×4的正方形网格中,是相似三角形的是( )
C
A. ①和②
B. ②和③
C. ①和③
D. ②和④
点拨:先看轮廓,再比较最长边和最短边.
思考:类似于判定三角形全等的 SAS 方法,能不能通过两边和夹角来判定两个三角形相似呢?
探究2 利用刻度尺和量角器画 △ABC和 △A′B′C′,使∠A=∠A′,
量出 BC 及 B′C′ 的长,它们的比值等于 k吗?
再量一量两个三角形另外的两个角,你有什么发现?△ABC 与 △A′B′C′ 有何关系?
答:两个三角形相似.
改变 k 和∠A 的值的大小,是否有同样的结论?
证明:在 △A′B′C′ 的边 A′B′ 上截取点D,
使 A′D = AB.过点 D 作 DE∥B′C′,
交 A′C′ 于点 E.
∵ DE∥B′C′,
∴ △A′DE∽△A′B′C′.
根据上述条件,求证:△ABC∽△A′B′C′.
B
A
C
D
E
B'
A'
C'
∴
∴ A′E = AC .
又 ∠A′ = ∠A,
∴ △A′DE ≌ △ABC,
∴ △ABC ∽△A′B′C′.
B
A
C
D
E
B'
A'
C'
∵ A′D=AB,
∴
由此得到利用两边和夹角来判定三角形相似的定理:
两边成比例且夹角相等的两个三角形相似.
符号语言:
∵ ∠A=∠A′,
∴ △ABC ∽ △A′B′C′ .
归 纳:
B
A
C
B'
A'
C'
思考:对于△ABC和 △A′B′C′,如果 ∠B= ∠B′,
这两个三角形一定会相似吗?试着画画看.
如图所示,
∠B=∠B'
有两种情况,所以
以上条件下,△ABC和△A'B'C'不一定相似.
若把∠B 换成∠C,情况一样.
A/A'
B
C
C'
B'
A/A'
B
C
C'
B'
结论:如果两个三角形两边对应成比例,但相等的角不是两条对应边的夹角,那么两个三角形不一定相似,相等的角一定要是两条对应边的夹角.
例2 如图,小正方形的边长均为1,则下列选项中的三角形(阴影部分)
与 相似的是( @2@ )
A B C D
A
点拨:找特殊角,
比较该角的两边
A
B
C
1.在 中, ,在 中, ,
,当 ______时, .
2.如图,四边形ABCD,CDEF,EFGH都是正方形.
(1)△ACF与△ACG相似吗?说说你的理由;
(2)求∠1+∠2的度数.
解:相似
解:45°
点拨:找相同角
点拨:将两角转化到一个三角形
相似三角形的判定
定理1,2
注意
要点
1.三边成比例
2.两边成比例且夹角相等
如果两个三角形两边对应成比例,但相等的角不是两条对应边的夹角,那么两个三角形不一定相似,相等的角一定要是两条对应边的夹角
27.2.1 相似三角形的判定
第2课时 相似三角形的判定定理1,2
1.探索用三边关系判定三角形相似定理
2.掌握利用三边来判定两个三角形相似的方法,并能进行相关计算. (重点、难点)
3.探索“两边成比例且夹角相等的两个三角形相似”的判定定理.
4.会根据边和角的关系来判定两个三角形相似,并进行相关计算. (重点、难点)
思考:学习三角形全等时,我们知道有判定两个三角形的简便方法(SSS、SAS、ASA、AAS).
类似于判定三角形全等 的SSS方法,我们能不能通过三边来判断两 个三角形相似呢?
回顾:上节课我们探究了平行线分线段成比例定理
任意画一个 △ABC ,再画一个 △A′B′C′,使它的各边长都是原来
△ABC 的各边长的k倍,动手量一量这两个三角形的角,它们分别
相等吗?这两个三角形相似吗?
A′
B′
C′
C
B
A
探究1 三边成比例的两个三角形相似
通过测量不难发现∠A=∠A',∠B=∠B',∠C=∠C',
又因为两个三角形的边对应成比例,所以 △ABC ∽△A′B′C′.
下面我们用前面所学定理证明该结论.
A′
B′
C′
C
B
A
∴
证明: 在线段 A′B′ (或延长线上)截取A′D=AB,
过点 D 作 DE∥B′C′ 交A′C′于点 E.
∵ DE∥B′C′ ,∴ △A′DE ∽ △A′B′C′.
又 ,A′D=AB,
C
B
A
B′
C′
A′
D
E
∴ DE=BC,A′E=AC.
∴△A′DE≌△ABC,
∴△ABC∽△A′B′C′ .
∴ , .
C
B
A
B′
C′
A′
D
E
由此我们得到利用三边判定三角形相似的定理:
三边成比例的两个三角形相似.
归 纳:
符号语言:
∵ ,
∴ △ ABC ∽ △A′B′C.
例1
如图,在大小为4×4的正方形网格中,是相似三角形的是( )
C
A. ①和②
B. ②和③
C. ①和③
D. ②和④
点拨:先看轮廓,再比较最长边和最短边.
思考:类似于判定三角形全等的 SAS 方法,能不能通过两边和夹角来判定两个三角形相似呢?
探究2 利用刻度尺和量角器画 △ABC和 △A′B′C′,使∠A=∠A′,
量出 BC 及 B′C′ 的长,它们的比值等于 k吗?
再量一量两个三角形另外的两个角,你有什么发现?△ABC 与 △A′B′C′ 有何关系?
答:两个三角形相似.
改变 k 和∠A 的值的大小,是否有同样的结论?
证明:在 △A′B′C′ 的边 A′B′ 上截取点D,
使 A′D = AB.过点 D 作 DE∥B′C′,
交 A′C′ 于点 E.
∵ DE∥B′C′,
∴ △A′DE∽△A′B′C′.
根据上述条件,求证:△ABC∽△A′B′C′.
B
A
C
D
E
B'
A'
C'
∴
∴ A′E = AC .
又 ∠A′ = ∠A,
∴ △A′DE ≌ △ABC,
∴ △ABC ∽△A′B′C′.
B
A
C
D
E
B'
A'
C'
∵ A′D=AB,
∴
由此得到利用两边和夹角来判定三角形相似的定理:
两边成比例且夹角相等的两个三角形相似.
符号语言:
∵ ∠A=∠A′,
∴ △ABC ∽ △A′B′C′ .
归 纳:
B
A
C
B'
A'
C'
思考:对于△ABC和 △A′B′C′,如果 ∠B= ∠B′,
这两个三角形一定会相似吗?试着画画看.
如图所示,
∠B=∠B'
有两种情况,所以
以上条件下,△ABC和△A'B'C'不一定相似.
若把∠B 换成∠C,情况一样.
A/A'
B
C
C'
B'
A/A'
B
C
C'
B'
结论:如果两个三角形两边对应成比例,但相等的角不是两条对应边的夹角,那么两个三角形不一定相似,相等的角一定要是两条对应边的夹角.
例2 如图,小正方形的边长均为1,则下列选项中的三角形(阴影部分)
与 相似的是( @2@ )
A B C D
A
点拨:找特殊角,
比较该角的两边
A
B
C
1.在 中, ,在 中, ,
,当 ______时, .
2.如图,四边形ABCD,CDEF,EFGH都是正方形.
(1)△ACF与△ACG相似吗?说说你的理由;
(2)求∠1+∠2的度数.
解:相似
解:45°
点拨:找相同角
点拨:将两角转化到一个三角形
相似三角形的判定
定理1,2
注意
要点
1.三边成比例
2.两边成比例且夹角相等
如果两个三角形两边对应成比例,但相等的角不是两条对应边的夹角,那么两个三角形不一定相似,相等的角一定要是两条对应边的夹角
