27.2.3 相似三角形应用举例 课件(共36张PPT) 2024-2025学年数学人教版九年级下册

(共36张PPT)
27.2.3 相似三角形应用举例
2.进一步了解数学建模思想，能够将实际问题转化为相似三角形的数学模型，提高分析问题、解决问题的能力（难点）
1.能够利用相似三角形的知识，求出不能直接测量的物体的高度和宽度（重点）
据传说，古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理，在金字塔影子的顶部立一根木杆，借助太阳光线构成两个相似三角形，来测量金字塔的高度.
又 ∠AOB =∠DFE = 90°，
∴△ABO ∽△DEF.
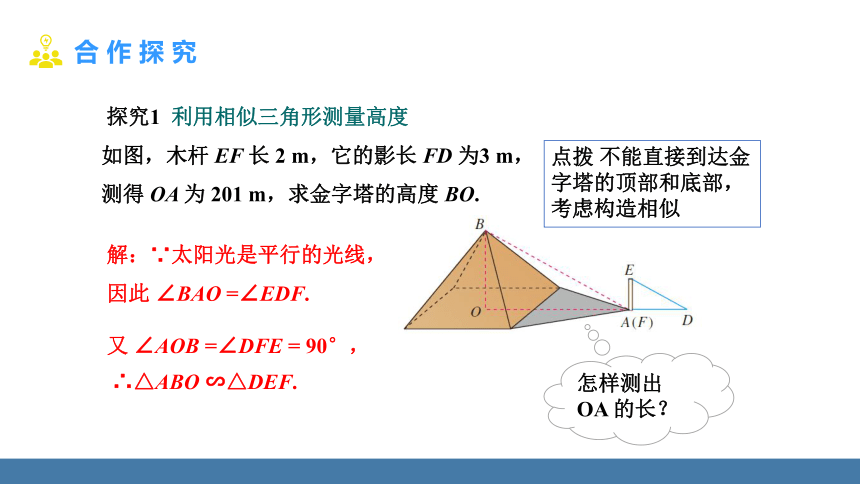
探究1 利用相似三角形测量高度
如图，木杆 EF 长 2 m，它的影长 FD 为3 m，
测得 OA 为 201 m，求金字塔的高度 BO.
解：∵太阳光是平行的光线，
因此 ∠BAO =∠EDF.
点拨 不能直接到达金字塔的顶部和底部，考虑构造相似
怎样测出
OA 的长？
表达式：物1高 ：物2高 = 影1长 ：影2长
归纳 测高方法一：
2.测量不能到达顶部的物体的高度，可以用“在同一时刻物
高与影长成正比例”的原理解决.
1.太阳离我们非常远，因此可以把太阳光近似地看
成平行光线
3.此方法要求被测物体的底部可以到达（或可以间接求出其影长）
例1 如图，要测量旗杆 AB 的高度，可在地面上竖一根竹竿 DE，
测量出 DE 的长以及 DE 和 AB在同一时刻下地面上的影长即可，
则下面能用于直接测量求 AB 长的等式是 ( )
A． B．
C． D．
C
例2 某一时刻,身高 的小明在阳光下的影长是 ,
同一时刻同一地点测得某旗杆的影长是 ,则该旗杆的
高度是________.

A
F
E
B
O
┐
┐
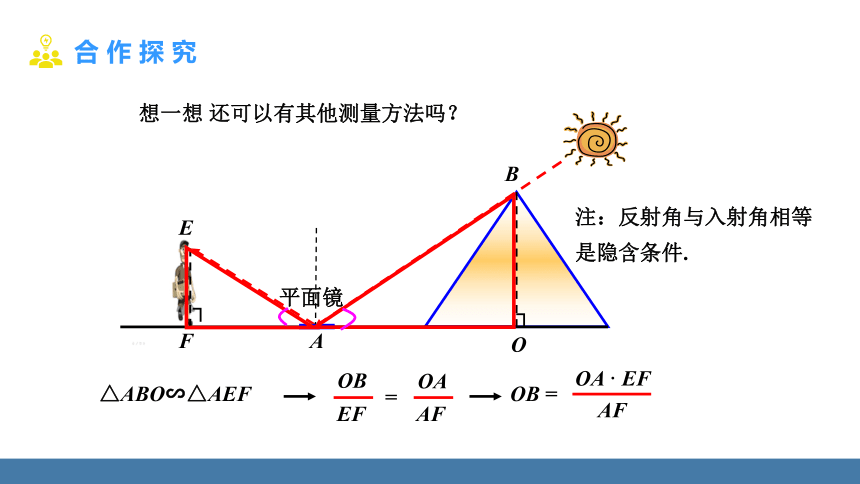
想一想 还可以有其他测量方法吗？
OB
EF
=
OA
AF
△ABO∽△AEF
OB =
OA · EF
AF
平面镜
注：反射角与入射角相等
是隐含条件.
归纳 测高方法二：
测量不能到达顶部的物体的高度，也可以用“利用镜子的反射测量高度”的原理解决.
例3 如图,有点光源 在平面镜上面,若在 点看到点光源的
反射光线,并测得 , , ,且
,则 的长度为_____ .

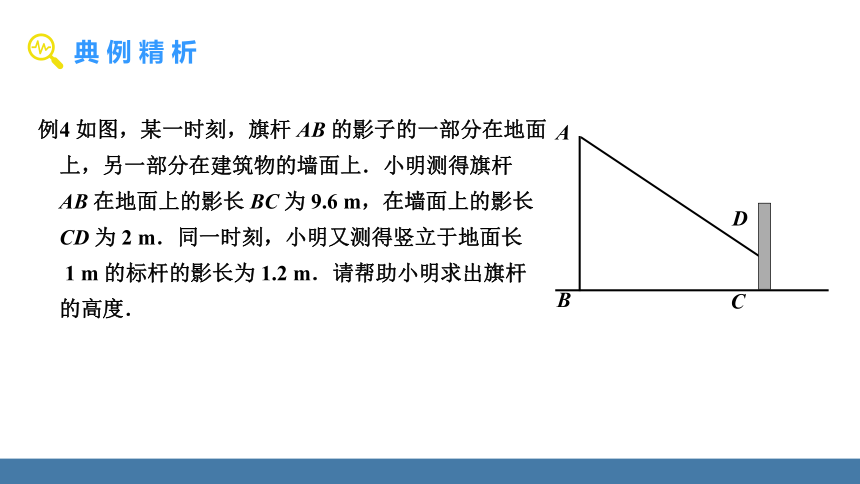
例4 如图，某一时刻，旗杆 AB 的影子的一部分在地面
上，另一部分在建筑物的墙面上．小明测得旗杆
AB 在地面上的影长 BC 为 9.6 m，在墙面上的影长
CD 为 2 m．同一时刻，小明又测得竖立于地面长
1 m 的标杆的影长为 1.2 m．请帮助小明求出旗杆
的高度．
A
B
C
D
E
解：如图，过点 D 作 DE∥BC，交 AB 于点 E，
∴ DE = CB = 9.6 m，BE = CD = 2 m．
∵ 在同一时刻物高与影长成正比例，
∴ EA : ED=1 : 1.2．
∴ AE = 8 m．
∴ AB = AE + EB = 8 + 2 = 10 (m)．
∴ 学校旗杆的高度为 10 m.
A
B
C
D
探究2 利用相似三角形测量宽度
如图，为了估算河的宽度，我们可以在河对岸选定一个目标点 P，在近岸取点 Q 和 S，使点 P，Q，S共线且直线 PS 与河垂直，接着在过点 S 且与 PS 垂直的直线 a 上选择适当的点 T，确定 PT 与过点 Q 且垂直 PS 的直线 b 的交点 R. 已知
测得QS = 45 m，ST = 90 m，QR = 60 m，请根据这些数据，
计算河宽 PQ.
P
R
Q
S
b
T
a
PQ×90 = (PQ+45)×60.
解得 PQ = 90（m）.
因此，河宽大约为 90 m.
解：∵∠PQR =∠PST =90°，∠P=∠P，
∴△PQR∽△PST.
P
R
Q
S
b
T
a
∴ ，
即 ，
还有其他构造相似三角形求河宽的方法吗？
45m
90m
60m
例5 如图, 于 , 于 ,测得 , ,
,则河宽 为______ .

测量如河宽等不易直接测量的物体的宽度，常构造相似三角形求解.
归纳：
”A”型
“X”型
探究3 利用相似解决有遮挡物问题
1.与测量有关的概念：
(1)视点：观察物体时人的眼睛称为视点．
(2)仰角：测量物体的高度时，水平视线与观察物
体的视线间的夹角称为仰角．
(3)盲区：人的视线看不到的区域称为盲区．
2.测量原理：用标杆或直尺作为三角形的边，利用视
点和盲区的知识构造相似三角形．
3.测量方法：如图，观测者的眼睛C必须与标杆的顶
端D和物体的顶端A“三点共线”，标杆与地面要
垂直，测量出标杆的高度DF， 人眼离地面的高度
CE，人与标杆的距离EF，标杆与 物体的距离FG. 利用相似三角形 “对应边的比相等”的性质求物体的高度AG.
如图，左、右并排的两棵大树的高分别是 AB =8 m 和 CD = 12 m，两树
底部的距离 BD = 5 m，一个人估计自己眼睛距离地面 1.6 m，她沿着正对这
两棵树的一条水平直路 l 从左向右前进，当她与左边较低的树的距离小于
多少时，就看不到右边较高的树的顶端C 了
分析：如图，设观察者眼睛的位置 (视点) 为点 F，画出观察者的水平视线 FG，
它交 AB，CD 于点 H，K.视线 FA，FG 的夹角 ∠AFH 是观察点 A 的仰角. 类似地，∠CFK 是观察点 C 时的仰角，由于树的遮挡，区域Ⅰ和Ⅱ都在观察者看不到的区域 (盲区) 之内. 再往前走就根本看不到 C 点了.
解：如图，假设观察者从左向右走到点 E 时，她的眼
睛的位置点 E 与两棵树的顶端点 A，C 恰在一条
直线上． ∵AB⊥l，CD⊥l，∴AB∥CD.
∴△AEH∽△CEK.
∴ ，
即
解得 EH=8.
由此可知，如果观察者继续前进，
当她与左边的树的距离小于 8 m 时，
由于这棵树的遮挡，就看不到右边树
的顶端 C .
提示：利用标杆或直尺测量物体的高度也叫目测，在日常生活中有着广泛的应用，必要时可以用自己的身高和臂长等作为测量工具．
归 纳
测量方法：测量不能到达顶部的物体的高度时，常常利用光线构造相似三角形(如同一时刻，物高与影长)来解决．常见的测量方式有四种，如图所示.
例6 如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上，已知纸板的两条直角边DE＝40 cm，EF＝20 cm，测得边DF离地面的高度AC＝1.5 m，CD＝8 m，则树高AB＝________m．　
5.5
1.要测量古塔的高度,下面方法不可取的是( @1@ )
A.利用同一时刻物体与其影长的比相等来求
B.利用直升机进行实物测量
C.利用镜面反射,借助于三角形相似来求
D.利用标杆,借助三角形相似来求
B
2.小明想利用树影测量树高，他在某一时刻测得长为1 m的竹竿影长0.9 m，但当他马上测量树影时，因树靠近一栋建筑物，影子不全落在地面上，有一部分影子在墙上，如图，他先测得留在墙上的影高l.2 m，又测得地面部分的影长2.7 m，那么树高是________.
4.2 m
3. 如图，为了估算池塘的宽度 ，在池塘边不远处选定一个目标点 ，
在近河边分别选 , .使得 , , 三点共线， , , 三点共线且
. 经测量 , , ,求池塘 的
宽度.
解： ，
，
, ，
，
， ，
.
答：池塘 的宽度为 .
4.某高中学校为高一新生设计的学生板凳从正面看到的平面图形如图所示，
其中 BA =CD，BC = 20 cm，BC 与 EF 平行于 AD，且到 AD 的距离分别为
40 cm，8 cm.为使板凳两腿底端 A，D 之间的距离为 30 cm，那么横梁 EF
应为多长？(材质及其厚度等忽略不计)
解：如图，过点 C 作 CM //AB，分别交 EF，AD 于点 N，M. 作 CP⊥AD，
分别交 EF，AD 于点 Q，P.
∵ BC//AD，EN//AD，
∴四边形 ABCM 和四边形 AENM 均是平行四边形，
∴EN =AM =BC = 20 cm，
∴ MD =AD -AM =30-20=10(cm).
由题意知 CP =40 cm，PQ =8 cm，
∴ CQ =CP - PQ =32 cm.
Q
P
N
M
∵ EF//AD，
∴△CNF∽△CMD.
∴ ，即 ，
解得 NF =8 cm.
∴ EF =EN +NF =20+8=28(cm).
答：横梁 EF 应为 28 cm.
N
M
Q
P
5.小琛周末去检查视力，发现该店老板利用平面镜来解决房间小的问题.已知正常情况下，人与视力表之间的距离应为5米，而测得该店两面墙的距离为3米.如图，根据平面镜成像原理作出光路图，视力表AB的上下边沿 ， 上发出的光线经平面镜 的上下边反射后射入人眼 处.已知视力表 的全长为0.8米，要使墙面上的镜子能呈现完整的视力表，请计算出镜长至少为多少米？
解：如图，作 于点 ，并延长交 于点 ，
， ，
， ，
又 米，
米，
米，
， 米，
答：镜长至少为0.32米.
相似三角形的应用举例
利用相似三角形测量高度
利用相似三角形测量宽度
利用相似解决有遮挡物问题