28.1.3 特殊角的锐角三角函数值 课件(共22张PPT) 2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 28.1.3 特殊角的锐角三角函数值 课件(共22张PPT) 2024-2025学年数学人教版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-12 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
28.1.3 特殊角的锐角三角函数值
1.推导并熟记30°,45°,60°角的三角函数值.
2.能运用30°,45°,60°角的三角函数值进行简单的计算.
3.能由30°,45°,60°角的三角函数值求对应的锐角.
说说锐角三角函数是如何定义的.
若∠A为30°,你能立即说出它对应的三角函数值吗?
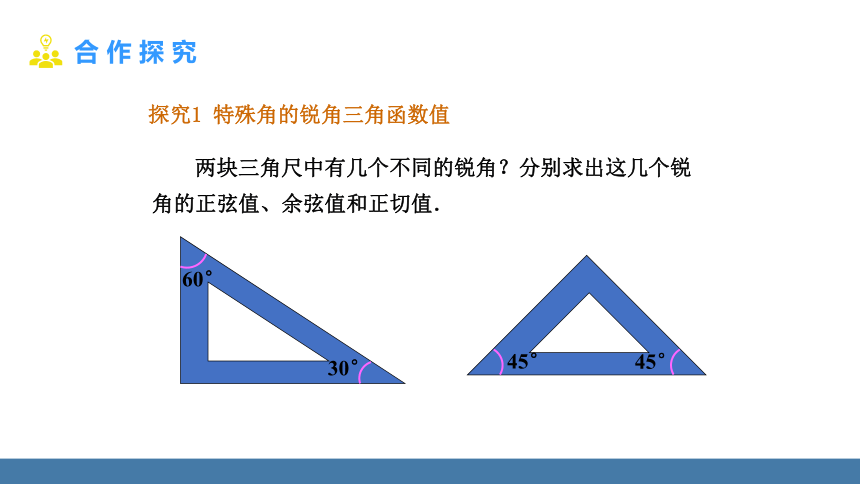
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
30°
60°
45°
45°
探究1 特殊角的锐角三角函数值
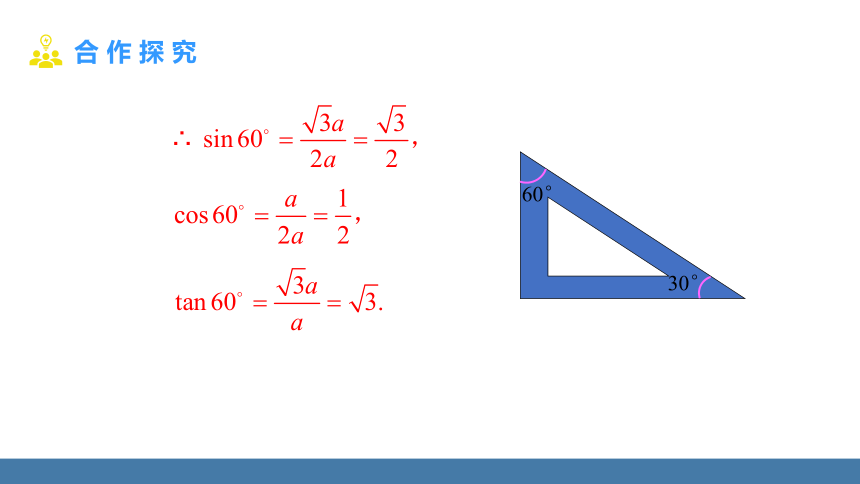
设30°所对的直角边长为a,那么斜边长为2a,
另一条直角边长 =
∴
30°
60°
∴
30°
60°
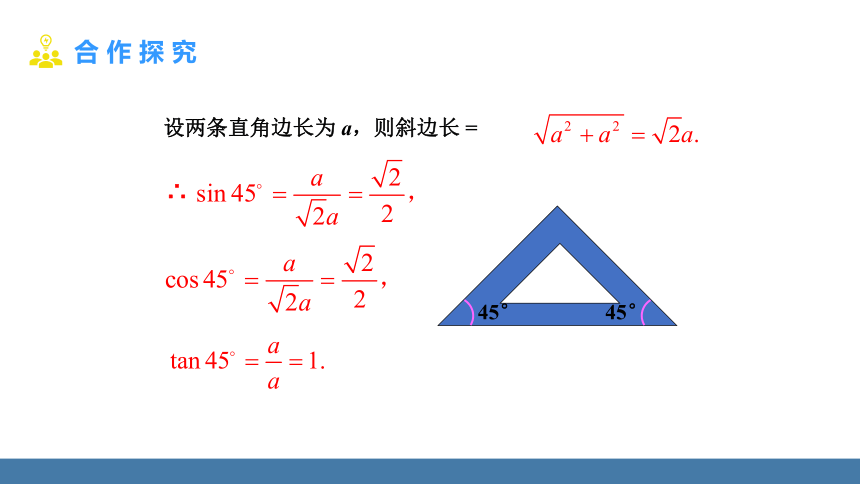
设两条直角边长为 a,则斜边长 =
∴
45°
45°
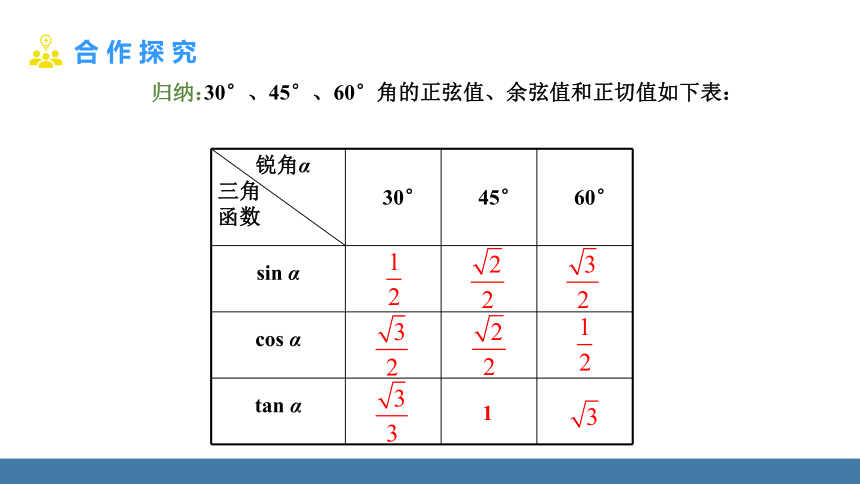
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角α 三角 函数 30° 45° 60°
sin α
cos α
tan α
归纳:
1
例1 求下列各式的值:
提示:cos260°表示(cos60°)2,即
(cos60°)×(cos60°).
解:cos260°+sin260°
(1) cos260°+sin260°;
(2)
解:
解: 在图中,
A
B
C
例2 (1) 如图,在Rt△ABC中,∠C = 90°,AB = ,
BC = ,求 ∠A 的度数;
∴ ∠A = 45°.
∵
解: 在图中,
A
B
O
∴ α = 60°.
∵ tanα = ,
(2) 如图,AO 是圆锥的高,OB 是底面半径,AO =
OB,求 α 的度数.
通过前面的学习,我们知道当锐角 A 是 30°、45°、60° 等特殊角时,
可以求得这些特殊角的三角函数值;如果锐角 A 不是这些特殊角,怎样得到
它的三角函数值呢?
探究2 用计算器求锐角的三角函数值或角的度数
例3 (1) 用计算器求 sin18° 的值;
解:第一步:按计算器上的 键;
sin
第二步:输入角度值 18;
第三步:按 “ = ” 号键,屏幕显示结果
0.309 016 994.
(2) 用计算器求 tan30°36′ 的值;
解:方法①:
第二步:输入角度值 30.6 (因为30°36′ = 30.6°);
第三步:按 “ = ” 号键,屏幕显示结果
0.591 398 351.
第一步:按计算器上的 键;
tan
第三步:按 “ = ” 号键,屏幕显示结果 0.591 398 351.
方法②:
第一步:按计算器上的 键;
tan
第二步:输入角度值 30,分值 36 (使用 键);
° ′ ″
(3) 已知 sinA = 0.501 8,用计算器求 ∠A 的度数.
第二步:然后输入正弦函数值 0. 501 8;
第三步:按 “ = ” 号键,屏幕显示结果
30.119 158 67° (按实际需要进行精确).
解:
第一步:按计算器上的 和 键;
2nd F
sin
还可以利用 和 键,进一步得到
∠A = 30°07′08.97″ (这说明锐角 A 精确到 1′ 的结果为 30°7′,精确到 1″ 的结果为 30°7′9″).
2nd F
° ′ ″
1.计算 的结果是( @2@ )
A. B. C. D.
B
2.随着锐角 的增大, 的值( @7@ )
A.增大 B.减小
C.不变 D.增大还是减小不确定
B
3.在△ABC中,∠A,∠B都是锐角,且 , ,则△ABC的形状是( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.不能确定
B
4.在 △ABC 中,若 ,则∠C = .
120°
5.通过计算 (可用计算器),比较下列各组数的大小,并提出你的猜想:
① sin30°____2sin15°cos15°;
② sin38°____2sin19°cos19°;
③ sin45°____2sin22.5°cos22.5°;
④ sin60°____2sin30°cos30°;
⑤ sin84°____2sin42°cos42°.
猜想:已知0°<α<45°,则sin2α___2sinαcosα.
=
=
=
=
=
=
30°、45°、60°角的三角函数值
通过三角函数值求角度
特殊角的三角函数值
28.1.3 特殊角的锐角三角函数值
1.推导并熟记30°,45°,60°角的三角函数值.
2.能运用30°,45°,60°角的三角函数值进行简单的计算.
3.能由30°,45°,60°角的三角函数值求对应的锐角.
说说锐角三角函数是如何定义的.
若∠A为30°,你能立即说出它对应的三角函数值吗?
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
30°
60°
45°
45°
探究1 特殊角的锐角三角函数值
设30°所对的直角边长为a,那么斜边长为2a,
另一条直角边长 =
∴
30°
60°
∴
30°
60°
设两条直角边长为 a,则斜边长 =
∴
45°
45°
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角α 三角 函数 30° 45° 60°
sin α
cos α
tan α
归纳:
1
例1 求下列各式的值:
提示:cos260°表示(cos60°)2,即
(cos60°)×(cos60°).
解:cos260°+sin260°
(1) cos260°+sin260°;
(2)
解:
解: 在图中,
A
B
C
例2 (1) 如图,在Rt△ABC中,∠C = 90°,AB = ,
BC = ,求 ∠A 的度数;
∴ ∠A = 45°.
∵
解: 在图中,
A
B
O
∴ α = 60°.
∵ tanα = ,
(2) 如图,AO 是圆锥的高,OB 是底面半径,AO =
OB,求 α 的度数.
通过前面的学习,我们知道当锐角 A 是 30°、45°、60° 等特殊角时,
可以求得这些特殊角的三角函数值;如果锐角 A 不是这些特殊角,怎样得到
它的三角函数值呢?
探究2 用计算器求锐角的三角函数值或角的度数
例3 (1) 用计算器求 sin18° 的值;
解:第一步:按计算器上的 键;
sin
第二步:输入角度值 18;
第三步:按 “ = ” 号键,屏幕显示结果
0.309 016 994.
(2) 用计算器求 tan30°36′ 的值;
解:方法①:
第二步:输入角度值 30.6 (因为30°36′ = 30.6°);
第三步:按 “ = ” 号键,屏幕显示结果
0.591 398 351.
第一步:按计算器上的 键;
tan
第三步:按 “ = ” 号键,屏幕显示结果 0.591 398 351.
方法②:
第一步:按计算器上的 键;
tan
第二步:输入角度值 30,分值 36 (使用 键);
° ′ ″
(3) 已知 sinA = 0.501 8,用计算器求 ∠A 的度数.
第二步:然后输入正弦函数值 0. 501 8;
第三步:按 “ = ” 号键,屏幕显示结果
30.119 158 67° (按实际需要进行精确).
解:
第一步:按计算器上的 和 键;
2nd F
sin
还可以利用 和 键,进一步得到
∠A = 30°07′08.97″ (这说明锐角 A 精确到 1′ 的结果为 30°7′,精确到 1″ 的结果为 30°7′9″).
2nd F
° ′ ″
1.计算 的结果是( @2@ )
A. B. C. D.
B
2.随着锐角 的增大, 的值( @7@ )
A.增大 B.减小
C.不变 D.增大还是减小不确定
B
3.在△ABC中,∠A,∠B都是锐角,且 , ,则△ABC的形状是( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.不能确定
B
4.在 △ABC 中,若 ,则∠C = .
120°
5.通过计算 (可用计算器),比较下列各组数的大小,并提出你的猜想:
① sin30°____2sin15°cos15°;
② sin38°____2sin19°cos19°;
③ sin45°____2sin22.5°cos22.5°;
④ sin60°____2sin30°cos30°;
⑤ sin84°____2sin42°cos42°.
猜想:已知0°<α<45°,则sin2α___2sinαcosα.
=
=
=
=
=
=
30°、45°、60°角的三角函数值
通过三角函数值求角度
特殊角的三角函数值
