29.1 投影 课件 2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 29.1 投影 课件 2024-2025学年数学人教版九年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-15 21:56:41 | ||
图片预览











文档简介
(共36张PPT)
29.1 投影
1.知道投影、投影面、平行投影和中心投影的概念.
2.能说出平行投影和中心投影的区别.
3.能利用平行投影和中心投影的相关知识解决实际问题.(重点、难点)
4. 了解正投影的概念.
5. 掌握线段、平面图形的正投影规律.(重点)
6. 能根据正投影的性质画出简单平面图形的正投影,
并进行相关计算.(重点、难点)
观察下列图片你发现了什么共同点?
这些图片里蕴含了一个什么数学原理呢?
这就是我们这节课要研究的问题——投影.
你知道物体与影子有什么关系吗?
一、投影的定义
一般地,用光线照射物体,在某个平面 (地面、墙壁等) 上得到的影子叫做物体的投影.
归 纳
投影面
投影
投影线
照射光线叫做投影线,投影所在的平面叫做投影面.
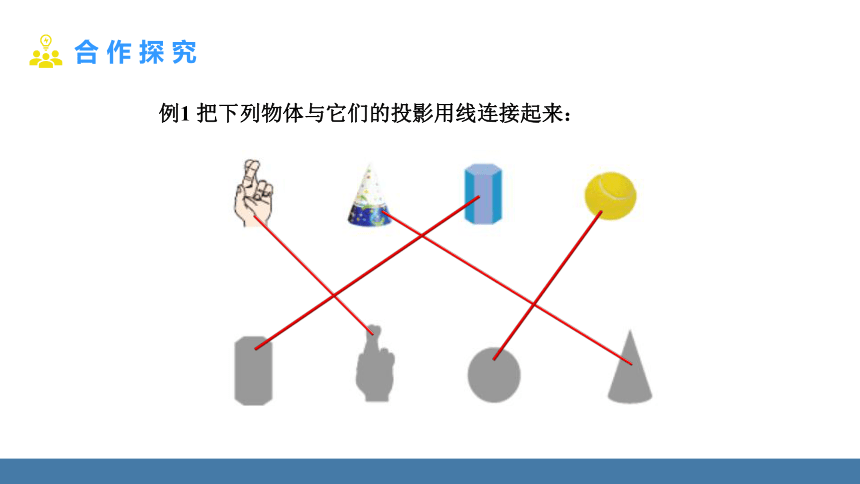
例1 把下列物体与它们的投影用线连接起来:
二、平行投影
观察下列图片,你认为太阳光线有什么特征?
太阳离我们非常遥远,太阳光线可以看成平行光线.
由平行光线形成的投影叫做平行投影.
探照灯发出的光线形成的投影是平行投影.
归 纳:
由同一点(点光源)发出的光线形成的投影叫做中心投影.
例如,物体在灯泡发出的光线照射下形成的影子就是中心投影.
三、中心投影
如何判断是平行投影还是中心投影?
通过光源来判断:
平行投影的光源为平行光线.
中心投影的光源为点光源.
平行投影的光源一般有探照灯、太阳光,其光线是平行的;
中心投影的光源一般有灯泡、 蜡烛,其光线相交于一点 .
平行投影和中心投影有什么区别和联系呢
区别 联系
平行投影
中心投影
投影线互相平行,
形成平行投影
投影线集中于一点,形成中心投影
都是物体在光线的照射下,在某个平面内形成的影子. (即都是投影)
例2 在下列四幅图形中,能表示两棵树在同一时刻阳光下影子的图形的
可能是( @3@ )
D
A. B. C. D.
例3太阳光透过一个矩形玻璃窗户,照射在地面上,影子的形状不可能是( @4@ )
A. 矩形 B. 正方形 C. 平行四边形 D. 一个点
D
(1) (2) (3)
上图表示一块三角尺在光线照射下形成的投影,其中哪个是平行投影?哪个是中心投影 图(2)(3)的投影线与投影面的位置关系有什么区别
思考:
(1) (2) (3)
图(2)(3)中投影线与投影面所成的夹角不同;
中心投影
平行投影
像图(3)中投影线垂直于投影面产生的投影叫做正投影,这节课我们研究正投影.
四、正投影
投影线垂直于投影面产生的投影叫做正投影.
正投影:投影线垂直于投影面
斜投影:投影线倾斜于投影面
正投影与斜投影的特点?
如图,把一根直的细铁丝 (记为线段AB) 放在三个不同位置.
p
A
B
A1
B1
A
B
A
B
A3(B3)
B2
A2
三种情形下铁丝的正投影各是什么形状?
(1) 铁丝平行于投影面;
(2)铁丝倾斜于投影面;
(3) 铁丝垂直于投影面 (铁丝不一定要与投影面有交点).
五、平面图形的正投影
(1) 当线段AB平行于投影面p时,它的正投影是线段A1B1,
线段与它的投影的大小关系为AB_____A1B1;
(2) 当线段AB倾斜于投影面p时,它的正投影是线段A2B2,
线段与它的投影的大小关系为AB______A2B2;
(3) 当线段AB垂直于投影面p时,它的正投影是一个
________.
通过观察,我们可以发现:
=
>
点A3(B3)
通过观察测量可知:
p
A
B
A1
B1
A
B
A
B
A3(B3)
B2
A2
如图,把一块正方形硬纸板P (记为正方形ABCD) 放在三个不同位置:
(1) 纸板平行于投影面; (2) 纸板倾斜于投影面;
(3) 纸板垂直于投影面.
三种情形下纸板的正投影各是什么形状?
A
B
C
D
A
B
C
D
A
B
C
D
q
(3) 当纸板P垂直于投影面q时,P的正投影成为
_______________.
通过观察、测量可知:
(1) 当纸板P平行于投影面q时,P的正投影与P的
_________________;
(2) 当纸板P倾斜于投影面q时,P的正投影与P的
___________________;
形状、大小一样
形状、大小发生变化
一条线段
通过观察、测量可知:
A
B
C
D
A'
B'
C'
D'
A
B
C
D
A'
B'
C'
D'
A
B
C
D
A'( B')
D'(C')
q
归 纳:
当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同.
例4 如图所示的水杯的杯口与投影面平行,投影线的方向如箭头所示,
则它的正投影是( @1@ )
A. B. C. D.
D
例5 画出如图摆放的正方体在投影面上的正投影.
(1)正方体的一个面ABCD平行于投影面;
分析:正方体的一个面ABCD及其相对的另一面与投影面平行,这两个面的正投影是与正方体的一个面的形状、大小完全相同的正方形A'B'C'D'.正方形A'B'C'D'的四条边分别是正方体其余四个面(这些面垂直于投影面)的投影. 因此,正方体的正投影是一个正方形.
六、画几何体的正投影
A
D
A′
B′
C′
D′
B
C
(2)正方体的一个面ABCD倾斜于投影面P,上底面ADEF垂直于投影面P,并且上底面的对角线AE垂直于投影面P).
分析:当正方体在图示的位置时,它的面ABCD和面ABGF倾斜于投影面,它们的投影分别是矩形A'B'C'D'和A'B'G'F';正方体其余两个侧面的投影分别是上述矩形;上、下底面的投影分别是线段D'F'和C'G'.因此,正方体的投影是矩形F'G'C'D',且线段A'B'把矩形一分为二.
C
D
E
F
G
D′
C′
B′
G′
A
H
A'
F'
例6 投影线的方向如箭头所示,画出图中圆柱体的正投影:
(1)
(2)
例7 画出下列立体图形投影线从上方射向下方的正投影.
解:如图所示:
例8 如图①,已知一根长 8 cm 的木棒 AB 平行于投影面
α,投影线垂直于 α. (1) 求影子 A1B1 的长度;
(2) 如图②,若将木棒绕其端点 A 逆时针旋转 30°,求旋转后木棒的影长 A2B2 .
解:(1) A1B1 = 8 cm.
E
(2) A2B2 = cm.
1.“皮影戏”是我国一种历史悠久的民间艺术,下列关于它的说法正确的是( @6@ )
A. 皮影戏的原理是利用平行投影将剪影投射到屏幕上
B. 屏幕上人物的身高与相应人物剪影的身高之比等于对应点到光源的距离之比
C. 屏幕上影像的面积等于相应剪影的面积
D. 表演时,也可以利用阳光把剪影投射到屏幕上
B
2.如图,夜晚路灯下有一排同样高的旗杆,离路灯越近,旗杆的影子( @3@ )
A.越长 B.越短
C.一样长 D.随时间变化而变化
B
3.正方形的正投影不可能 是( @4@ )
A.线段 B.矩形 C.正方形 D.梯形
D
4.如图,棱长为 的正方体的侧棱与平面 H 平行,其上、下底面的对角线 AC,A1C1 与平面 H 垂直.
(1)作出该正方体在平面 H 上的正投影;
解:(1)该正方体在平面 H 上的正投影为如图所示的矩形 MNPQ.
(2)计算投影的面积.
解:(2)∵ 正方体的棱长
为 ,
∴ 由勾股定理得
BD = =2,
∴ 投影 MNPQ 的面积为 2×=2.
投影
投影的概念
平行投影与中心投影
投影作图
正投影
正投影的概念及性质
几何体的正投影
平面图形的正投影
29.1 投影
1.知道投影、投影面、平行投影和中心投影的概念.
2.能说出平行投影和中心投影的区别.
3.能利用平行投影和中心投影的相关知识解决实际问题.(重点、难点)
4. 了解正投影的概念.
5. 掌握线段、平面图形的正投影规律.(重点)
6. 能根据正投影的性质画出简单平面图形的正投影,
并进行相关计算.(重点、难点)
观察下列图片你发现了什么共同点?
这些图片里蕴含了一个什么数学原理呢?
这就是我们这节课要研究的问题——投影.
你知道物体与影子有什么关系吗?
一、投影的定义
一般地,用光线照射物体,在某个平面 (地面、墙壁等) 上得到的影子叫做物体的投影.
归 纳
投影面
投影
投影线
照射光线叫做投影线,投影所在的平面叫做投影面.
例1 把下列物体与它们的投影用线连接起来:
二、平行投影
观察下列图片,你认为太阳光线有什么特征?
太阳离我们非常遥远,太阳光线可以看成平行光线.
由平行光线形成的投影叫做平行投影.
探照灯发出的光线形成的投影是平行投影.
归 纳:
由同一点(点光源)发出的光线形成的投影叫做中心投影.
例如,物体在灯泡发出的光线照射下形成的影子就是中心投影.
三、中心投影
如何判断是平行投影还是中心投影?
通过光源来判断:
平行投影的光源为平行光线.
中心投影的光源为点光源.
平行投影的光源一般有探照灯、太阳光,其光线是平行的;
中心投影的光源一般有灯泡、 蜡烛,其光线相交于一点 .
平行投影和中心投影有什么区别和联系呢
区别 联系
平行投影
中心投影
投影线互相平行,
形成平行投影
投影线集中于一点,形成中心投影
都是物体在光线的照射下,在某个平面内形成的影子. (即都是投影)
例2 在下列四幅图形中,能表示两棵树在同一时刻阳光下影子的图形的
可能是( @3@ )
D
A. B. C. D.
例3太阳光透过一个矩形玻璃窗户,照射在地面上,影子的形状不可能是( @4@ )
A. 矩形 B. 正方形 C. 平行四边形 D. 一个点
D
(1) (2) (3)
上图表示一块三角尺在光线照射下形成的投影,其中哪个是平行投影?哪个是中心投影 图(2)(3)的投影线与投影面的位置关系有什么区别
思考:
(1) (2) (3)
图(2)(3)中投影线与投影面所成的夹角不同;
中心投影
平行投影
像图(3)中投影线垂直于投影面产生的投影叫做正投影,这节课我们研究正投影.
四、正投影
投影线垂直于投影面产生的投影叫做正投影.
正投影:投影线垂直于投影面
斜投影:投影线倾斜于投影面
正投影与斜投影的特点?
如图,把一根直的细铁丝 (记为线段AB) 放在三个不同位置.
p
A
B
A1
B1
A
B
A
B
A3(B3)
B2
A2
三种情形下铁丝的正投影各是什么形状?
(1) 铁丝平行于投影面;
(2)铁丝倾斜于投影面;
(3) 铁丝垂直于投影面 (铁丝不一定要与投影面有交点).
五、平面图形的正投影
(1) 当线段AB平行于投影面p时,它的正投影是线段A1B1,
线段与它的投影的大小关系为AB_____A1B1;
(2) 当线段AB倾斜于投影面p时,它的正投影是线段A2B2,
线段与它的投影的大小关系为AB______A2B2;
(3) 当线段AB垂直于投影面p时,它的正投影是一个
________.
通过观察,我们可以发现:
=
>
点A3(B3)
通过观察测量可知:
p
A
B
A1
B1
A
B
A
B
A3(B3)
B2
A2
如图,把一块正方形硬纸板P (记为正方形ABCD) 放在三个不同位置:
(1) 纸板平行于投影面; (2) 纸板倾斜于投影面;
(3) 纸板垂直于投影面.
三种情形下纸板的正投影各是什么形状?
A
B
C
D
A
B
C
D
A
B
C
D
q
(3) 当纸板P垂直于投影面q时,P的正投影成为
_______________.
通过观察、测量可知:
(1) 当纸板P平行于投影面q时,P的正投影与P的
_________________;
(2) 当纸板P倾斜于投影面q时,P的正投影与P的
___________________;
形状、大小一样
形状、大小发生变化
一条线段
通过观察、测量可知:
A
B
C
D
A'
B'
C'
D'
A
B
C
D
A'
B'
C'
D'
A
B
C
D
A'( B')
D'(C')
q
归 纳:
当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同.
例4 如图所示的水杯的杯口与投影面平行,投影线的方向如箭头所示,
则它的正投影是( @1@ )
A. B. C. D.
D
例5 画出如图摆放的正方体在投影面上的正投影.
(1)正方体的一个面ABCD平行于投影面;
分析:正方体的一个面ABCD及其相对的另一面与投影面平行,这两个面的正投影是与正方体的一个面的形状、大小完全相同的正方形A'B'C'D'.正方形A'B'C'D'的四条边分别是正方体其余四个面(这些面垂直于投影面)的投影. 因此,正方体的正投影是一个正方形.
六、画几何体的正投影
A
D
A′
B′
C′
D′
B
C
(2)正方体的一个面ABCD倾斜于投影面P,上底面ADEF垂直于投影面P,并且上底面的对角线AE垂直于投影面P).
分析:当正方体在图示的位置时,它的面ABCD和面ABGF倾斜于投影面,它们的投影分别是矩形A'B'C'D'和A'B'G'F';正方体其余两个侧面的投影分别是上述矩形;上、下底面的投影分别是线段D'F'和C'G'.因此,正方体的投影是矩形F'G'C'D',且线段A'B'把矩形一分为二.
C
D
E
F
G
D′
C′
B′
G′
A
H
A'
F'
例6 投影线的方向如箭头所示,画出图中圆柱体的正投影:
(1)
(2)
例7 画出下列立体图形投影线从上方射向下方的正投影.
解:如图所示:
例8 如图①,已知一根长 8 cm 的木棒 AB 平行于投影面
α,投影线垂直于 α. (1) 求影子 A1B1 的长度;
(2) 如图②,若将木棒绕其端点 A 逆时针旋转 30°,求旋转后木棒的影长 A2B2 .
解:(1) A1B1 = 8 cm.
E
(2) A2B2 = cm.
1.“皮影戏”是我国一种历史悠久的民间艺术,下列关于它的说法正确的是( @6@ )
A. 皮影戏的原理是利用平行投影将剪影投射到屏幕上
B. 屏幕上人物的身高与相应人物剪影的身高之比等于对应点到光源的距离之比
C. 屏幕上影像的面积等于相应剪影的面积
D. 表演时,也可以利用阳光把剪影投射到屏幕上
B
2.如图,夜晚路灯下有一排同样高的旗杆,离路灯越近,旗杆的影子( @3@ )
A.越长 B.越短
C.一样长 D.随时间变化而变化
B
3.正方形的正投影
A.线段 B.矩形 C.正方形 D.梯形
D
4.如图,棱长为 的正方体的侧棱与平面 H 平行,其上、下底面的对角线 AC,A1C1 与平面 H 垂直.
(1)作出该正方体在平面 H 上的正投影;
解:(1)该正方体在平面 H 上的正投影为如图所示的矩形 MNPQ.
(2)计算投影的面积.
解:(2)∵ 正方体的棱长
为 ,
∴ 由勾股定理得
BD = =2,
∴ 投影 MNPQ 的面积为 2×=2.
投影
投影的概念
平行投影与中心投影
投影作图
正投影
正投影的概念及性质
几何体的正投影
平面图形的正投影
