必修五基本不等式课件
图片预览




文档简介
课件12张PPT。§ 3.4 基本不等式问题情境用你的座号数和同桌的座号数做一个游戏:左边的同学计算两座号数的平方和,右边的同学计算两座号数的积的两倍(单独坐的同学都用自己的座号),比较结果大小。你发现什么规律?能用数学式子表示吗? 新课讲解当且仅当 时,等号成立你能给出证明吗?那么a2+b2≥2 a b(当且仅当a=b时,取“=”号)若a∈R,b∈R若a>0,b>0如果a>0,b>0我们用 、 去替
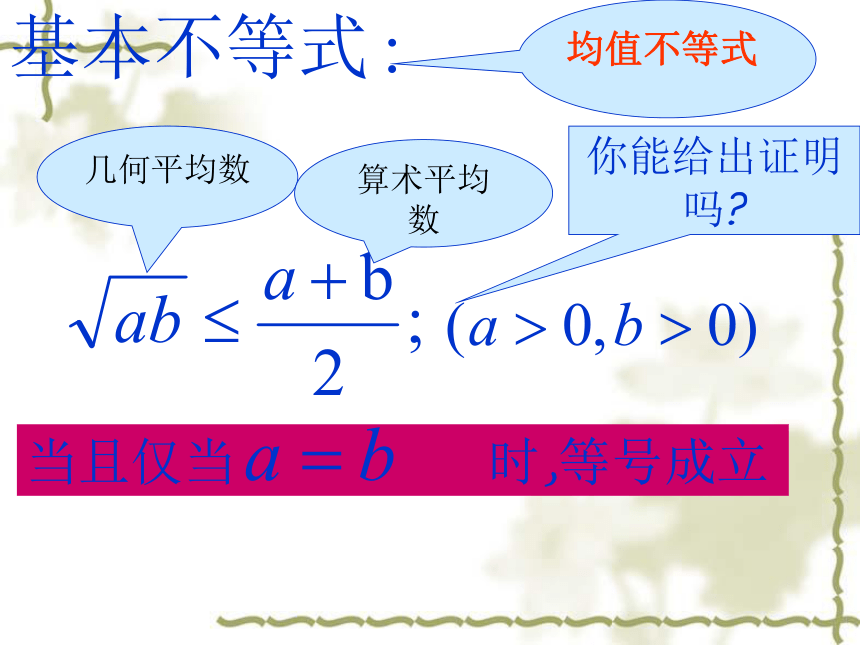
换a、b,能得到什么结论?
那么a + b ≥2 当且仅当 时,等号成立你能给出证明吗?几何平均数算术平均数均值不等式
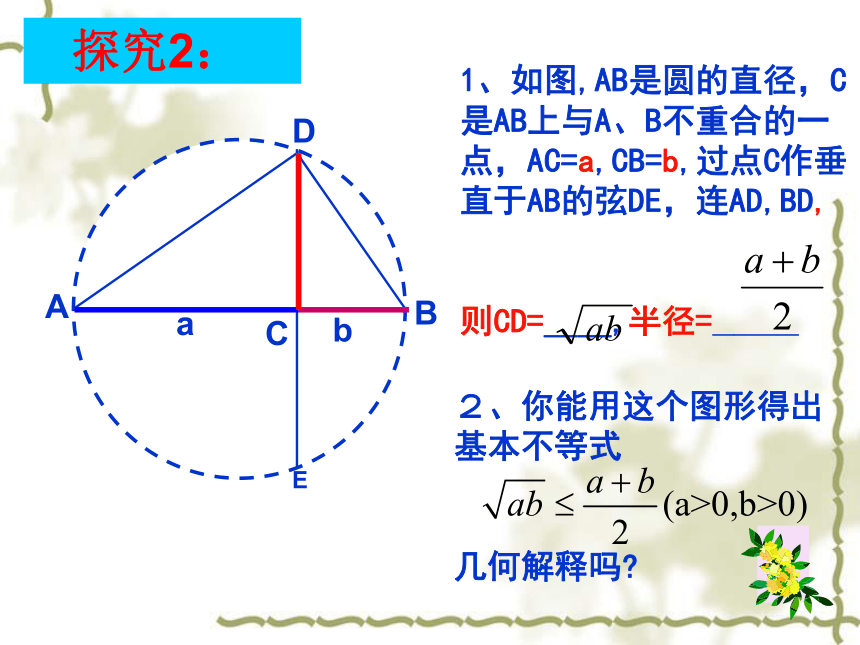
探究2:ABCDE1、如图,AB是圆的直径,C是AB上与A、B不重合的一点,AC=a,CB=b,过点C作垂直于AB的弦DE,连AD,BD,
则CD=__,半径=____2、你能用这个图形得出基本不等式
几何解释吗?ab当且仅当 时,等号成立例1:若a>0,b>0,且a+b=3,则当且仅当_______时,ab有最 __ 值为________.
例2:若a>0,b>0,且ab=3,则当且仅当_______时,a+b有最 ___ 值为________.
两个正数:和定积最大,积定和最小。变式训练1:(1)若X>0,求 的最小值;求最值条件:
一正二定三相等 当且仅当x=1/x时,即x=1时等号成立,y最小值为2.(2)求 的最值;
例题讲解例3:(1)用篱笆围一个面积为100 平方米的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短。最短的篱笆是多少?(2)用一段长为36m的篱笆围成一个矩形菜园,问这个矩形菜园的长和宽各为多少时,菜园的面积最大,最大面积是多少?课堂小结1、本节课主要学习了基本不等式的证明与初步应用。2、注意公式的正向、逆向使用的条件以
及“=”成立的条件。 (1)若a,b∈R,那么a2+b2≥2ab (当且仅当a=b时,取“=”号) (2) (当且仅当a=b时,取“=”号) 3、基本不等式求最值条件:一正二定三相等
作业与思考:1、作业
课本第100页习题3.4A第1﹑2题。
2、思考题:若x>3 ,求 的最小值
换a、b,能得到什么结论?
那么a + b ≥2 当且仅当 时,等号成立你能给出证明吗?几何平均数算术平均数均值不等式
探究2:ABCDE1、如图,AB是圆的直径,C是AB上与A、B不重合的一点,AC=a,CB=b,过点C作垂直于AB的弦DE,连AD,BD,
则CD=__,半径=____2、你能用这个图形得出基本不等式
几何解释吗?ab当且仅当 时,等号成立例1:若a>0,b>0,且a+b=3,则当且仅当_______时,ab有最 __ 值为________.
例2:若a>0,b>0,且ab=3,则当且仅当_______时,a+b有最 ___ 值为________.
两个正数:和定积最大,积定和最小。变式训练1:(1)若X>0,求 的最小值;求最值条件:
一正二定三相等 当且仅当x=1/x时,即x=1时等号成立,y最小值为2.(2)求 的最值;
例题讲解例3:(1)用篱笆围一个面积为100 平方米的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短。最短的篱笆是多少?(2)用一段长为36m的篱笆围成一个矩形菜园,问这个矩形菜园的长和宽各为多少时,菜园的面积最大,最大面积是多少?课堂小结1、本节课主要学习了基本不等式的证明与初步应用。2、注意公式的正向、逆向使用的条件以
及“=”成立的条件。 (1)若a,b∈R,那么a2+b2≥2ab (当且仅当a=b时,取“=”号) (2) (当且仅当a=b时,取“=”号) 3、基本不等式求最值条件:一正二定三相等
作业与思考:1、作业
课本第100页习题3.4A第1﹑2题。
2、思考题:若x>3 ,求 的最小值
