3.1.2 函数的单调性 教学设计
文档属性
| 名称 | 3.1.2 函数的单调性 教学设计 |
|
|
| 格式 | docx | ||
| 文件大小 | 78.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-14 00:00:00 | ||
图片预览


文档简介
《函数的单调性》教学设计
学习目标
1.通过从形与数两方面理解函数单调性的概念的学习,初步掌握利用函数图象和定义判断、证明函数单调性的方法.
2.通过对函数单调性定义的探究学习,培养学生观察能力和分析能力;通过对函数单调性的证明,提高学生的推理论证能力.
教学重点:函数单调性的概念、判断及证明.
教学难点:根据定义证明函数的单调性.
【教学过程】
一、归纳探索,形成概念
1.观察图象,直观感知
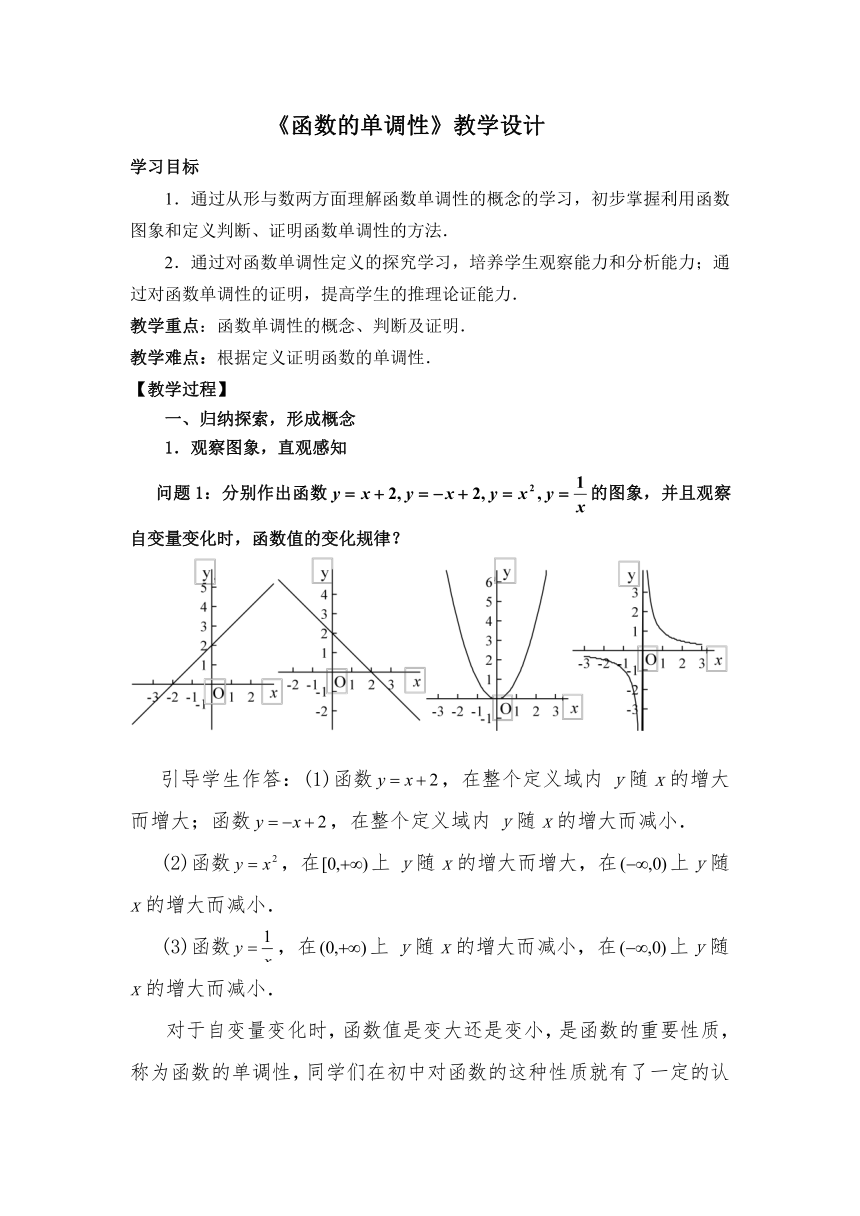
问题1:分别作出函数的图象,并且观察自变量变化时,函数值的变化规律?
引导学生作答:(1)函数,在整个定义域内 y随x的增大而增大;函数,在整个定义域内 y随x的增大而减小.
(2)函数,在上 y随x的增大而增大,在上y随x的增大而减小.
(3)函数,在上 y随x的增大而减小,在上y随x的增大而减小.
对于自变量变化时,函数值是变大还是变小,是函数的重要性质,称为函数的单调性,同学们在初中对函数的这种性质就有了一定的认识,但是没有严格的定义,今天我们就建立了函数单调性的定义.
问题2:能不能根据自己的理解说说什么是增函数、减函数吗
引导学生:如果函数在某个区间上随自变量x的增大,y也越来越大,我们说函数在该区间上为增函数;如果函数在某个区间上随自变量x的增大,y越来越小,我们说函数在该区间上为减函数.
教师指出:这种认识是从图象的角度得到的,是对函数单调性的直观、描述性的认识.
设计意图:从图象直观感知函数单调性,完成对函数单调性的初步认识.
2.思维提升,形成概念
问题1:如图是函数y=f(x)的图像,你能说出这个函数分别在哪些区间为增函数,哪些区间上为减函数?(图略见课本29页,多媒体展示)
学生能很快作答,但困难是有时难以确定分界点的确切位置.
通过讨论展示,使学生感受到用函数图象判断函数单调性虽然比较直观,但有时不够精确,需要结合解析式进一步进行研究.
设计意图:使学生体会到用数量大小关系严格表述函数单调性的必要性.
问题2:如何从解析式的角度说明在上为增函数?
(1) 在给定区间内取两个数,例如2和3,因为22<32,所以在上为增函数.
(2) 仿(1),取多组数值验证均满足,所以在为增函数.
(3) 任取,因为,即,所以在上为增函数.
对于学生错误的回答,引导学生分别用图形语言和文字语言进行辨析,使学生认识到问题的根源在于自变量不可能无限列举,从而引导学生在给定的区间内任意取两个自变量.
设计意图:把对单调性的认识由感性上升到理性认识的高度,完成对概念的第二次认识.事实上也给出了证明单调性的方法,为下阶段的学习做好铺垫.
二、掌握证法,适当延展
例1 证明函数在上是增函数.
1.分析解决问题
针对学生可能出现的问题,组织学生讨论、交流.
证明:任取, 设元
求差
变形
,
∴
∴即
∴函数在上是增函数.
2.归纳解题步骤
引导学生归纳证明函数单调性的步骤:设元、作差、变形、断号、定论.
练习:证明函数在上是增函数.
问题:除了用定义外,如果证得对任意的,且有,能断定函数在区间上是增函数吗
引导学生分析这种叙述与定义的等价性.让学生尝试用这种等价形式证明函数在上是增函数.
设计意图:初步掌握根据定义证明函数单调性的方法和步骤.了解等价形式进一步发展可以得到导数法,为今后用导数方法研究函数单调性埋下伏笔.
三、归纳小结,巩固提高
学生分组交流在本节课学习中的体会、收获,交流学习过程中的体验和感受,完成小结.
1. 直观到抽象、特殊到一般、感性到理性.
2.方法和步骤:设元、作差、变形、断号、定论.
3.数形结合的思想方法.
学习目标
1.通过从形与数两方面理解函数单调性的概念的学习,初步掌握利用函数图象和定义判断、证明函数单调性的方法.
2.通过对函数单调性定义的探究学习,培养学生观察能力和分析能力;通过对函数单调性的证明,提高学生的推理论证能力.
教学重点:函数单调性的概念、判断及证明.
教学难点:根据定义证明函数的单调性.
【教学过程】
一、归纳探索,形成概念
1.观察图象,直观感知
问题1:分别作出函数的图象,并且观察自变量变化时,函数值的变化规律?
引导学生作答:(1)函数,在整个定义域内 y随x的增大而增大;函数,在整个定义域内 y随x的增大而减小.
(2)函数,在上 y随x的增大而增大,在上y随x的增大而减小.
(3)函数,在上 y随x的增大而减小,在上y随x的增大而减小.
对于自变量变化时,函数值是变大还是变小,是函数的重要性质,称为函数的单调性,同学们在初中对函数的这种性质就有了一定的认识,但是没有严格的定义,今天我们就建立了函数单调性的定义.
问题2:能不能根据自己的理解说说什么是增函数、减函数吗
引导学生:如果函数在某个区间上随自变量x的增大,y也越来越大,我们说函数在该区间上为增函数;如果函数在某个区间上随自变量x的增大,y越来越小,我们说函数在该区间上为减函数.
教师指出:这种认识是从图象的角度得到的,是对函数单调性的直观、描述性的认识.
设计意图:从图象直观感知函数单调性,完成对函数单调性的初步认识.
2.思维提升,形成概念
问题1:如图是函数y=f(x)的图像,你能说出这个函数分别在哪些区间为增函数,哪些区间上为减函数?(图略见课本29页,多媒体展示)
学生能很快作答,但困难是有时难以确定分界点的确切位置.
通过讨论展示,使学生感受到用函数图象判断函数单调性虽然比较直观,但有时不够精确,需要结合解析式进一步进行研究.
设计意图:使学生体会到用数量大小关系严格表述函数单调性的必要性.
问题2:如何从解析式的角度说明在上为增函数?
(1) 在给定区间内取两个数,例如2和3,因为22<32,所以在上为增函数.
(2) 仿(1),取多组数值验证均满足,所以在为增函数.
(3) 任取,因为,即,所以在上为增函数.
对于学生错误的回答,引导学生分别用图形语言和文字语言进行辨析,使学生认识到问题的根源在于自变量不可能无限列举,从而引导学生在给定的区间内任意取两个自变量.
设计意图:把对单调性的认识由感性上升到理性认识的高度,完成对概念的第二次认识.事实上也给出了证明单调性的方法,为下阶段的学习做好铺垫.
二、掌握证法,适当延展
例1 证明函数在上是增函数.
1.分析解决问题
针对学生可能出现的问题,组织学生讨论、交流.
证明:任取, 设元
求差
变形
,
∴
∴即
∴函数在上是增函数.
2.归纳解题步骤
引导学生归纳证明函数单调性的步骤:设元、作差、变形、断号、定论.
练习:证明函数在上是增函数.
问题:除了用定义外,如果证得对任意的,且有,能断定函数在区间上是增函数吗
引导学生分析这种叙述与定义的等价性.让学生尝试用这种等价形式证明函数在上是增函数.
设计意图:初步掌握根据定义证明函数单调性的方法和步骤.了解等价形式进一步发展可以得到导数法,为今后用导数方法研究函数单调性埋下伏笔.
三、归纳小结,巩固提高
学生分组交流在本节课学习中的体会、收获,交流学习过程中的体验和感受,完成小结.
1. 直观到抽象、特殊到一般、感性到理性.
2.方法和步骤:设元、作差、变形、断号、定论.
3.数形结合的思想方法.
