北师大版九年级下3.4.2圆周角和圆心角的关系(二)课件(13张ppt)
文档属性
| 名称 | 北师大版九年级下3.4.2圆周角和圆心角的关系(二)课件(13张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-18 00:00:00 | ||
图片预览




文档简介
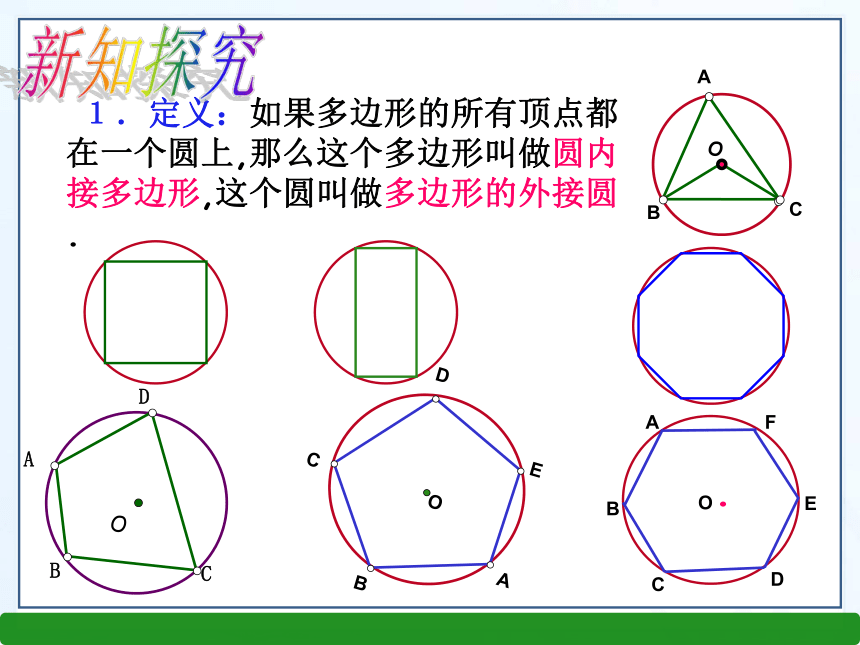
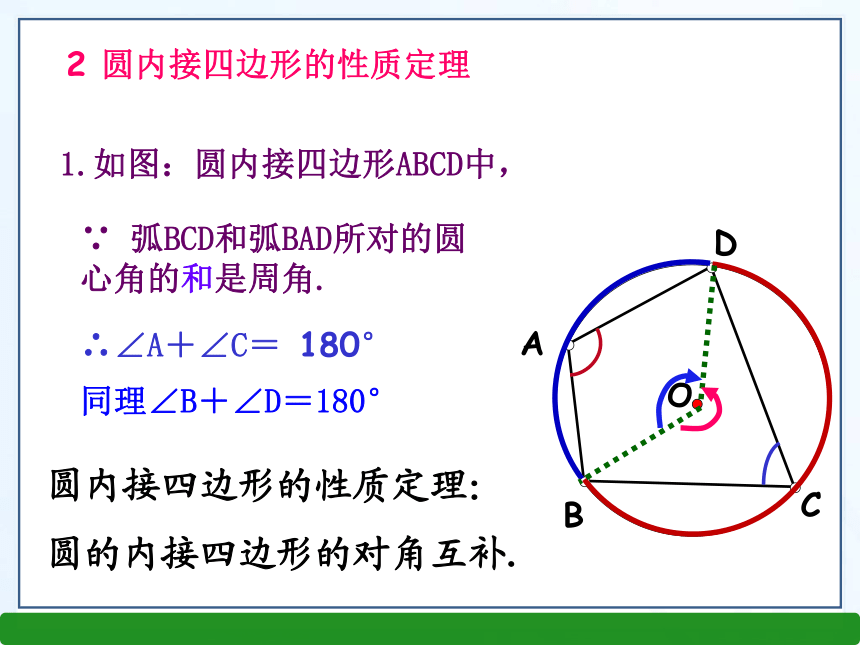
课件13张PPT。圆周角和圆心角的关系(二)第三章 圆什么是圆周角定理?圆心角的度数与它所对弧的度数是什么关系?圆周角定理:圆周角度数等于它所对的圆心角度数的一半。圆心角定理:圆心角的度数等于它所对弧的度数.知识回顾情境引入根据圆周角定理,在圆中,直径所对的圆周角是什么角?90°的圆周角所对的弦是直径吗?试作图观察,回答上面的问题?推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等;反之,相等的圆周角所对的弧也相等.推论2:半圆(或直径)所对的圆周角是直角;反之,90°的圆周角所对的弦是直径.自主预习 1.定义:如果多边形的所有顶点都在一个圆上,那么这个多边形叫做圆内接多边形,这个圆叫做多边形的外接圆.新知探究CODBA1.如图:圆内接四边形ABCD中,∵ 弧BCD和弧BAD所对的圆心角的和是周角.∴∠A+∠C= 180° 同理∠B+∠D=180°2 圆内接四边形的性质定理圆内接四边形的性质定理:
圆的内接四边形的对角互补.圆内接四边形的性质定理:
圆的内接四边形的对角互补.1、如图,四边形ABCD为⊙O的
内接四边形,已知∠BOD=100°,
则∠BAD= ,∠BCD= .2、圆内接四边形ABCD中,∠A:∠B:∠C=2:3:4,
则∠A= ∠B= ∠C= ∠D=50o130o60o90o120o90o3、如图,四边形ABCD内接于⊙O, ∠DCE=75o,则∠BOD=150o设A=2x,则C=4x. ∵A+C=180o, ∴x=30o.随堂练习4.如图9,弦AB,CD相交于E点,若∠BAC =27°,∠BEC =64°,则∠AOD等于( ).
A.37° B.74° C.54 D.64°
5.如图10,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于( ).A.69°B.42°C.48° D.38°看谁解答好又快!
6、如图6, ⊙O的直径 AB 为10 cm,弦 AC 为6 cm,∠ACB 的平分线交⊙O于 D,求BC、AD、BD的长.讲万卷书,行万里路7.已知:如图14,⊙O的直径AE=10cm,∠B=∠EAC.求AC的长.(图14)少壮不努力,老大徒伤悲8.已知:如图,△ABC内接于⊙O,AM平分∠BAC交⊙O于点M,AD⊥BC于D.
求证:∠MAO=∠MAD.
2 圆内接四边形的性质:圆的内接四边形的对角互补.
3、解题时应注意两点:
(1)认准直径所对的圆周角,灵活应用直角来求解。(2)注意观察图形,分清四边形的对角,利用它们的和来解答题目。知识梳理1、直径(或半圆)所对的圆周角是直角
圆的内接四边形的对角互补.圆内接四边形的性质定理:
圆的内接四边形的对角互补.1、如图,四边形ABCD为⊙O的
内接四边形,已知∠BOD=100°,
则∠BAD= ,∠BCD= .2、圆内接四边形ABCD中,∠A:∠B:∠C=2:3:4,
则∠A= ∠B= ∠C= ∠D=50o130o60o90o120o90o3、如图,四边形ABCD内接于⊙O, ∠DCE=75o,则∠BOD=150o设A=2x,则C=4x. ∵A+C=180o, ∴x=30o.随堂练习4.如图9,弦AB,CD相交于E点,若∠BAC =27°,∠BEC =64°,则∠AOD等于( ).
A.37° B.74° C.54 D.64°
5.如图10,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于( ).A.69°B.42°C.48° D.38°看谁解答好又快!
6、如图6, ⊙O的直径 AB 为10 cm,弦 AC 为6 cm,∠ACB 的平分线交⊙O于 D,求BC、AD、BD的长.讲万卷书,行万里路7.已知:如图14,⊙O的直径AE=10cm,∠B=∠EAC.求AC的长.(图14)少壮不努力,老大徒伤悲8.已知:如图,△ABC内接于⊙O,AM平分∠BAC交⊙O于点M,AD⊥BC于D.
求证:∠MAO=∠MAD.
2 圆内接四边形的性质:圆的内接四边形的对角互补.
3、解题时应注意两点:
(1)认准直径所对的圆周角,灵活应用直角来求解。(2)注意观察图形,分清四边形的对角,利用它们的和来解答题目。知识梳理1、直径(或半圆)所对的圆周角是直角
