2024-2025学年北师大版八年级数学上册 2.1认识无理数 课件(共20张PPT)
文档属性
| 名称 | 2024-2025学年北师大版八年级数学上册 2.1认识无理数 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 473.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-16 20:33:12 | ||
图片预览



文档简介
(共20张PPT)
2.1认识无理数
2024-2025学年北师大版八年级数学上册教学课件★★
教学目标
1、理解无理数的概念和其存在的意义,学会无理数的表示;
2、掌握常见的无理数类型,可以判断一个数是否是无理数;
复习提问
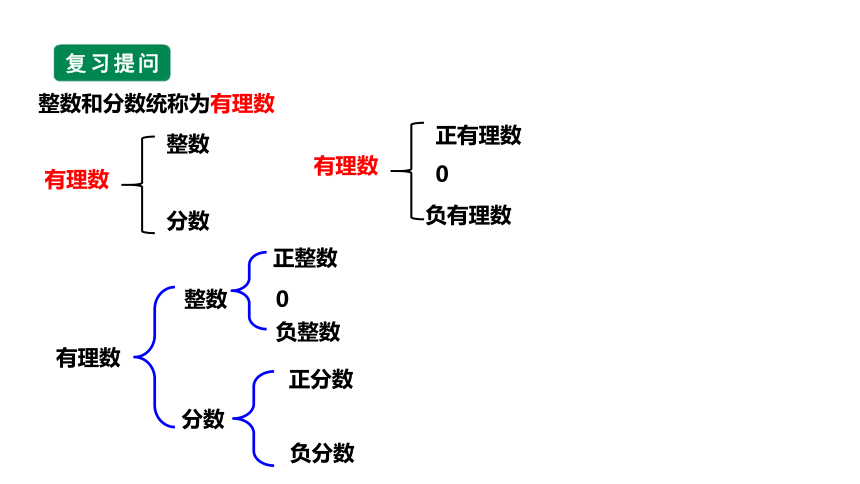
整数和分数统称为有理数
有理数
整数
分数
有理数
正有理数
负有理数
0
有理数
整数
正整数
负整数
分数
正分数
负分数
0
情境导入
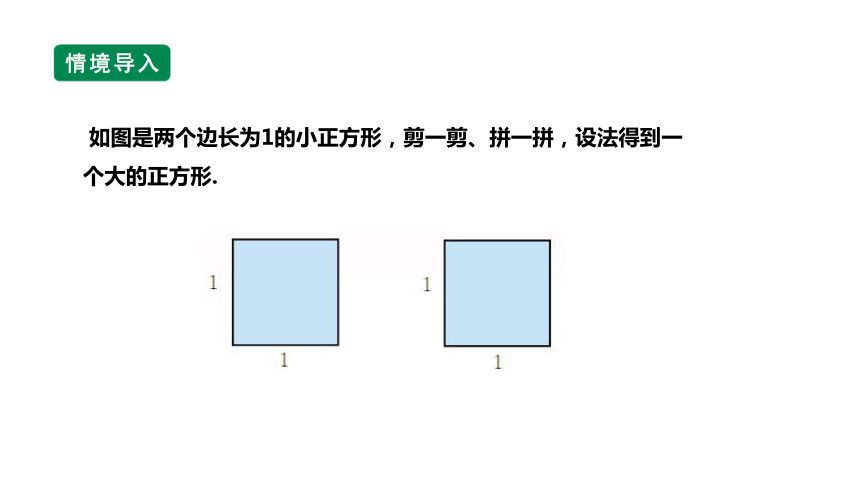
如图是两个边长为1的小正方形,剪一剪、拼一拼,设法得到一个大的正方形.
新知讲解
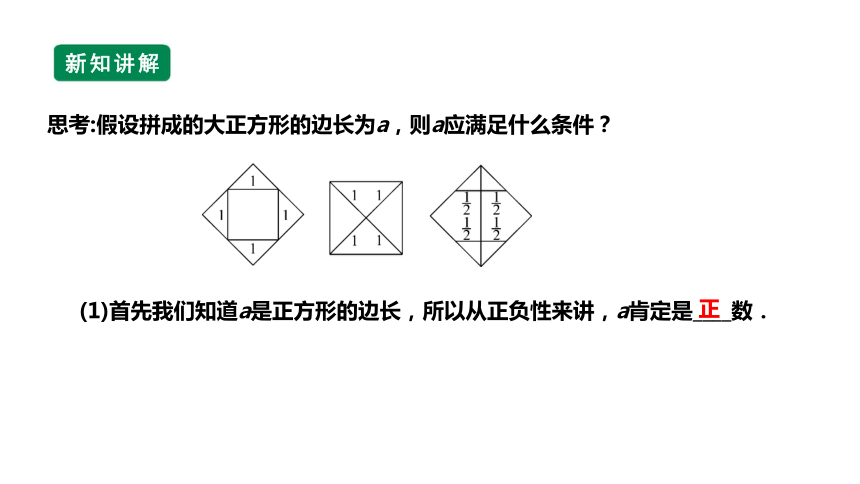
思考:假设拼成的大正方形的边长为a,则a应满足什么条件?
(1)首先我们知道a是正方形的边长,所以从正负性来讲,a肯定是____数.
正
新知讲解
(2)再来看看拼接后的正方形的面积,因为两个小正方形的面积之和等于大正方形的面积,所以可以计算出新拼接后的大正方形的面积为____.
2
∵a2=2,1∵a2=2,∴a不是分数
a既不是整数,也不是分数,那么一定不是有理数
(3)a可能是整数吗?说说你的理由.
(4)a可能是分数吗?说说你的理由,并与同伴进行交流.
做一做
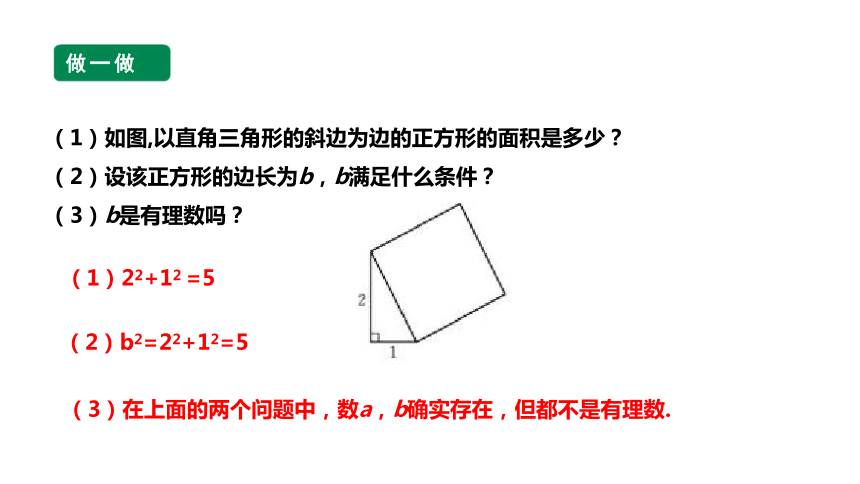
(1)如图,以直角三角形的斜边为边的正方形的面积是多少?
(2)设该正方形的边长为b,b满足什么条件?
(3)b是有理数吗?
(3)在上面的两个问题中,数a,b确实存在,但都不是有理数.
(1)22+12 =5
(2)b2=22+12=5
新知讲解
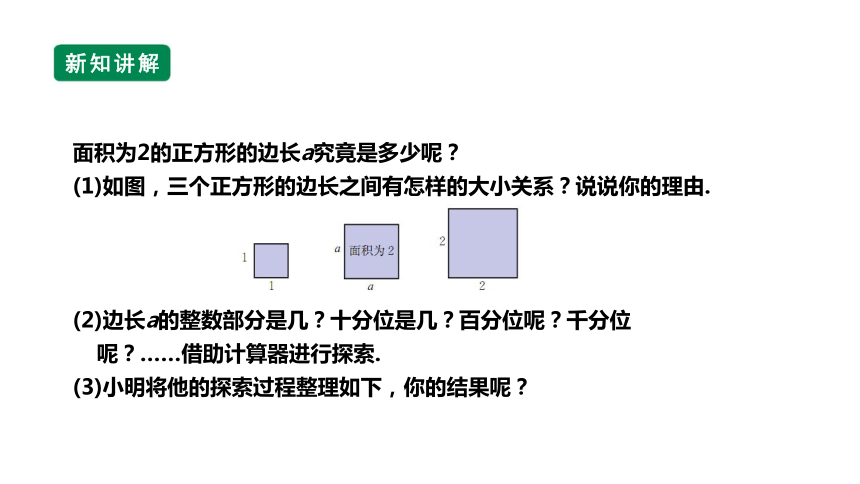
面积为2的正方形的边长a究竟是多少呢?
(1)如图,三个正方形的边长之间有怎样的大小关系?说说你的理由.
(2)边长a的整数部分是几?十分位是几?百分位呢?千分位呢?……借助计算器进行探索.
(3)小明将他的探索过程整理如下,你的结果呢?
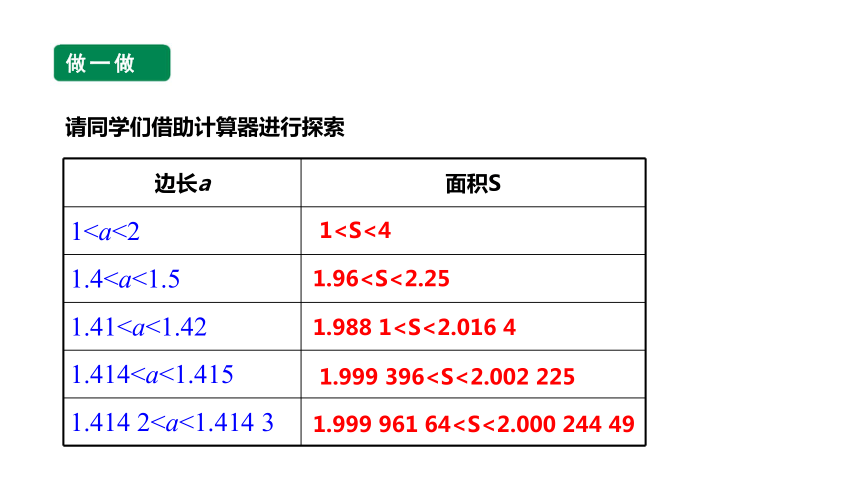
做一做
请同学们借助计算器进行探索
边长a 面积S
11.41.411.4141.414 211.961.988 11.999 3961.999 961 64做一做
①边长a会不会算到某一位时,它的平方恰好等于2呢?
②a可能是有限小数吗?它会是一个怎样的数呢?
a=1.414 213 56…, 它是一个无限不循环小数
会
做一做
(1)估计面积为5的正方形的边长b的值(结果精确到0.1 ),并用计算器验证你的估计.
(2)如果结果精确到0.01呢?
事实上,b=2.236 067 978…它是
一个无限不循环小数.
同样,对于体积为2的正方体,借助计算器,可以得到它的棱长c=1.259 921 05…它也是一个无限不循环小数.
议一议
使用计算器计算,把下列有理数写成小数的形式,你有什么发现?
3,
解:3=3.0,
,
事实上,有理数总可以用有限小数或无限循环小数表示.反过来,任何有限小数或无限循环小数也都是有理数.
要点归纳
无理数
(1)无理数的定义:无限不循环小数称为无理数.
(2)无理数的类型:
①上述中的a,b类型的;
②圆周率π型的;
③如0.585 885 888 588 885…(相邻两个5之间8的个数逐次加1)这种规定型的.
典例精析
例 下列各数中,哪些是有理数?哪些是无理数?
解:有理数有:
无理数有:0.101 000 100 000 1…(相邻
两个1之间0的个数逐次加2).
课堂练习
1.下列各数中,是有理数的是( )
A.面积为3的正方形的边长
B.体积为8的正方体的棱长
C.两直角边分别为1和2的直角三角形的斜边长
D.长为3,宽为2的长方形的对角线长
2.下列一组数:-8,2.5,30,π, 0.161616 … ,0.6,0.080 080 008…(相邻两个8之间依次增加一个0),其中无理数有 ( )
A.0个 B.1个 C.2个 D.3个
B
C
课堂练习
3.如图,在方格纸中,假设每个小正方形的面积为2,则图中的四条线段中长度是有理数的线段是______________.
CD 和EF
课堂练习
4.面积为7的正方形的边长为x.请你回答下列问题:
(1)x的整数部分是多少?
(2)把x的值精确到十分位时是多少?精确到百分位呢?
(3)x是有理数吗?请说明理由.
设正方形的面积为S,则S=x2=7.
当2<x<3时,4<S<9;
当2.6<x<2.7时,6.76<S<7.29;
当2.64<x<2.65时,6.969 6<S<7.022 5;
当2.645<x<2.646时,6.996 025<S<7.001 316.
课堂练习
(1)x的整数部分是2.
(2)把x的值精确到十分位时,x≈2.6;精确到百分位时,x≈2.65.
(3)x不是有理数.理由:由计算可知,
x是无限不循环小数,所以x不是有理数.
课堂总结
本节课你学到了什么?
1.无理数的特征:
(1)无理数的小数部分位数无限.
(2)无理数的小数部分不循环,不能表示成分数的形式.
2.常见的无理数的形式:
(1)无限不循环的小数;
(2)特殊字母,如“π”;
(3)an=b(n为大于1的自然数)中b为有理数,则a可能为无理数.
板书设计
2.1认识无理数
1.无理数是无限不循环小数,有理数是有限小数或无限循环小数.
2.任何一个有理数都可以化成分数形式( p≠0, p,q 为整数且互质)而无理数则不能.
2.1认识无理数
2024-2025学年北师大版八年级数学上册教学课件★★
教学目标
1、理解无理数的概念和其存在的意义,学会无理数的表示;
2、掌握常见的无理数类型,可以判断一个数是否是无理数;
复习提问
整数和分数统称为有理数
有理数
整数
分数
有理数
正有理数
负有理数
0
有理数
整数
正整数
负整数
分数
正分数
负分数
0
情境导入
如图是两个边长为1的小正方形,剪一剪、拼一拼,设法得到一个大的正方形.
新知讲解
思考:假设拼成的大正方形的边长为a,则a应满足什么条件?
(1)首先我们知道a是正方形的边长,所以从正负性来讲,a肯定是____数.
正
新知讲解
(2)再来看看拼接后的正方形的面积,因为两个小正方形的面积之和等于大正方形的面积,所以可以计算出新拼接后的大正方形的面积为____.
2
∵a2=2,1
a既不是整数,也不是分数,那么一定不是有理数
(3)a可能是整数吗?说说你的理由.
(4)a可能是分数吗?说说你的理由,并与同伴进行交流.
做一做
(1)如图,以直角三角形的斜边为边的正方形的面积是多少?
(2)设该正方形的边长为b,b满足什么条件?
(3)b是有理数吗?
(3)在上面的两个问题中,数a,b确实存在,但都不是有理数.
(1)22+12 =5
(2)b2=22+12=5
新知讲解
面积为2的正方形的边长a究竟是多少呢?
(1)如图,三个正方形的边长之间有怎样的大小关系?说说你的理由.
(2)边长a的整数部分是几?十分位是几?百分位呢?千分位呢?……借助计算器进行探索.
(3)小明将他的探索过程整理如下,你的结果呢?
做一做
请同学们借助计算器进行探索
边长a 面积S
1
①边长a会不会算到某一位时,它的平方恰好等于2呢?
②a可能是有限小数吗?它会是一个怎样的数呢?
a=1.414 213 56…, 它是一个无限不循环小数
会
做一做
(1)估计面积为5的正方形的边长b的值(结果精确到0.1 ),并用计算器验证你的估计.
(2)如果结果精确到0.01呢?
事实上,b=2.236 067 978…它是
一个无限不循环小数.
同样,对于体积为2的正方体,借助计算器,可以得到它的棱长c=1.259 921 05…它也是一个无限不循环小数.
议一议
使用计算器计算,把下列有理数写成小数的形式,你有什么发现?
3,
解:3=3.0,
,
事实上,有理数总可以用有限小数或无限循环小数表示.反过来,任何有限小数或无限循环小数也都是有理数.
要点归纳
无理数
(1)无理数的定义:无限不循环小数称为无理数.
(2)无理数的类型:
①上述中的a,b类型的;
②圆周率π型的;
③如0.585 885 888 588 885…(相邻两个5之间8的个数逐次加1)这种规定型的.
典例精析
例 下列各数中,哪些是有理数?哪些是无理数?
解:有理数有:
无理数有:0.101 000 100 000 1…(相邻
两个1之间0的个数逐次加2).
课堂练习
1.下列各数中,是有理数的是( )
A.面积为3的正方形的边长
B.体积为8的正方体的棱长
C.两直角边分别为1和2的直角三角形的斜边长
D.长为3,宽为2的长方形的对角线长
2.下列一组数:-8,2.5,30,π, 0.161616 … ,0.6,0.080 080 008…(相邻两个8之间依次增加一个0),其中无理数有 ( )
A.0个 B.1个 C.2个 D.3个
B
C
课堂练习
3.如图,在方格纸中,假设每个小正方形的面积为2,则图中的四条线段中长度是有理数的线段是______________.
CD 和EF
课堂练习
4.面积为7的正方形的边长为x.请你回答下列问题:
(1)x的整数部分是多少?
(2)把x的值精确到十分位时是多少?精确到百分位呢?
(3)x是有理数吗?请说明理由.
设正方形的面积为S,则S=x2=7.
当2<x<3时,4<S<9;
当2.6<x<2.7时,6.76<S<7.29;
当2.64<x<2.65时,6.969 6<S<7.022 5;
当2.645<x<2.646时,6.996 025<S<7.001 316.
课堂练习
(1)x的整数部分是2.
(2)把x的值精确到十分位时,x≈2.6;精确到百分位时,x≈2.65.
(3)x不是有理数.理由:由计算可知,
x是无限不循环小数,所以x不是有理数.
课堂总结
本节课你学到了什么?
1.无理数的特征:
(1)无理数的小数部分位数无限.
(2)无理数的小数部分不循环,不能表示成分数的形式.
2.常见的无理数的形式:
(1)无限不循环的小数;
(2)特殊字母,如“π”;
(3)an=b(n为大于1的自然数)中b为有理数,则a可能为无理数.
板书设计
2.1认识无理数
1.无理数是无限不循环小数,有理数是有限小数或无限循环小数.
2.任何一个有理数都可以化成分数形式( p≠0, p,q 为整数且互质)而无理数则不能.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
