第二十三章 旋转 单元练习(含答案) 2024-2025学年人教版数学九年级上册
文档属性
| 名称 | 第二十三章 旋转 单元练习(含答案) 2024-2025学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 494.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-17 09:01:39 | ||
图片预览

文档简介
第二十三章旋转 单元测试
一、单选题
1.在下列图案中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.如图,将绕点逆时针旋转到,点恰好落在边上,已知,则的长为( )
A. B. C. D.
3.如图,将绕点逆时针旋转后得到,点,的对应点分别为,,点恰好在边上,且点在的延长线上,连接,若,则下列结论一定正确的是( )
A. B.
C.旋转角是 D.
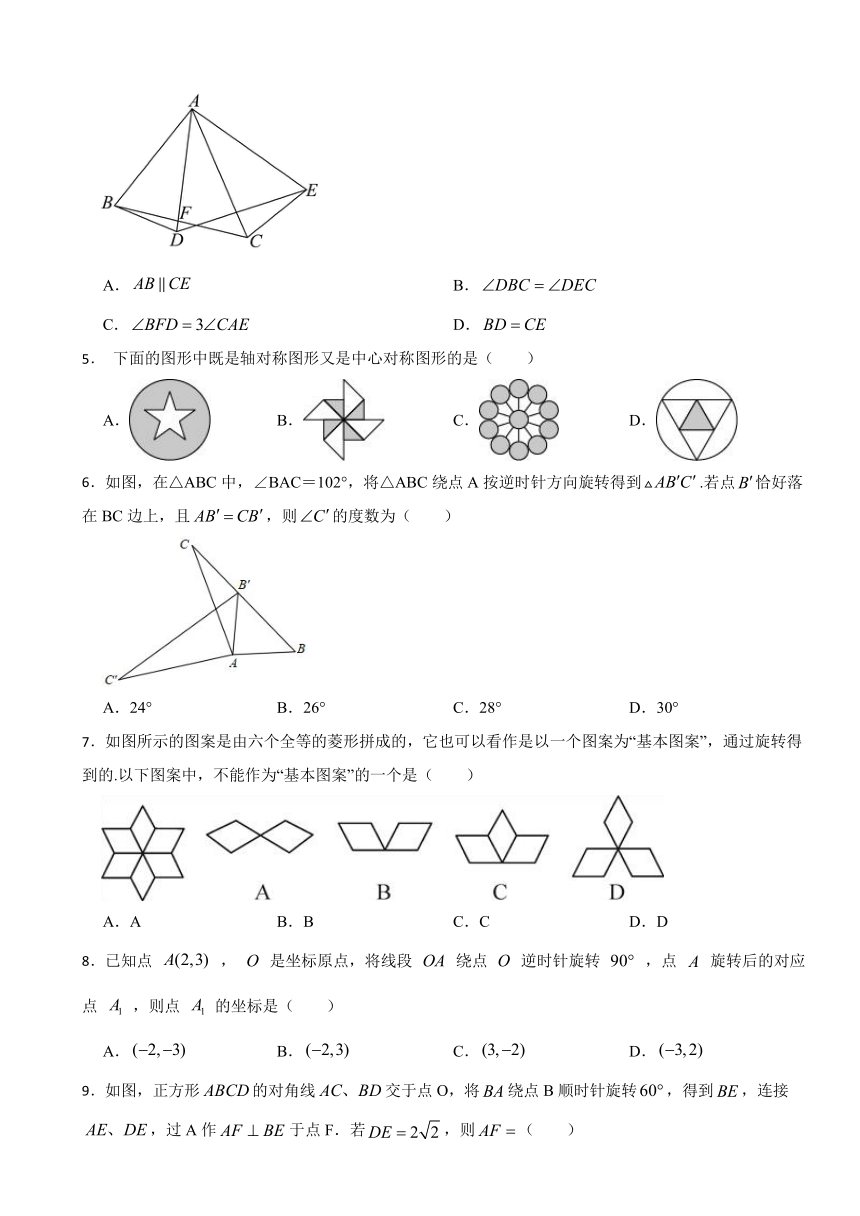
4.如图, 在中, , 以点为中心逆时针旋转得到, 点, 的对应点分别是点, , 且平分, 交于点, 则下列结论一定正确的是( )
A. B.
C. D.
5. 下面的图形中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
6.如图,在△ABC中,∠BAC=102°,将△ABC绕点A按逆时针方向旋转得到.若点恰好落在BC边上,且,则的度数为( )
A.24° B.26° C.28° D.30°
7.如图所示的图案是由六个全等的菱形拼成的,它也可以看作是以一个图案为“基本图案”,通过旋转得到的.以下图案中,不能作为“基本图案”的一个是( )
A.A B.B C.C D.D
8.已知点 , 是坐标原点,将线段 绕点 逆时针旋转 ,点 旋转后的对应点 ,则点 的坐标是( )
A. B. C. D.
9.如图,正方形的对角线交于点O,将绕点B顺时针旋转,得到,连接,过A作于点F.若,则( )
A. B. C. D.
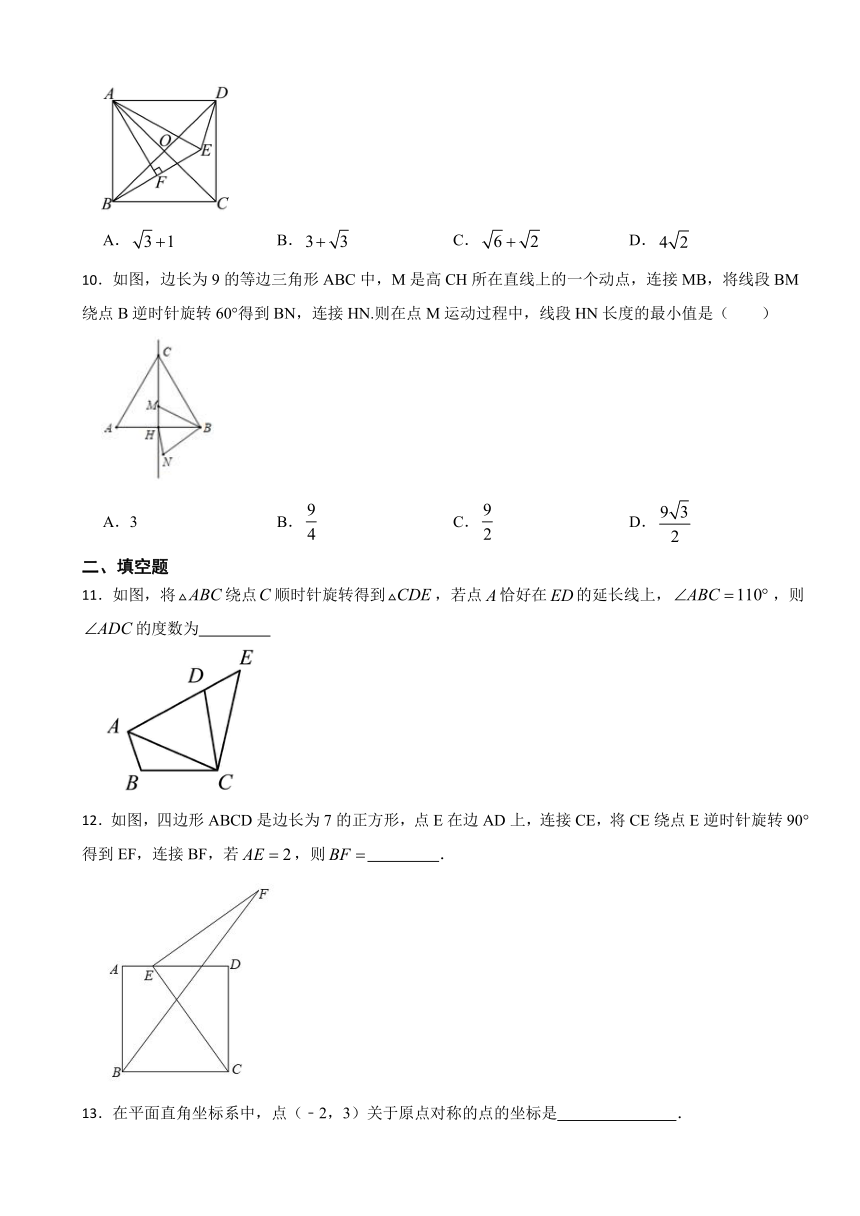
10.如图,边长为9的等边三角形ABC中,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是( )
A.3 B. C. D.
二、填空题
11.如图,将绕点顺时针旋转得到,若点恰好在的延长线上,,则的度数为
12.如图,四边形ABCD是边长为7的正方形,点E在边AD上,连接CE,将CE绕点E逆时针旋转90°得到EF,连接BF,若,则 .
13.在平面直角坐标系中,点(﹣2,3)关于原点对称的点的坐标是 .
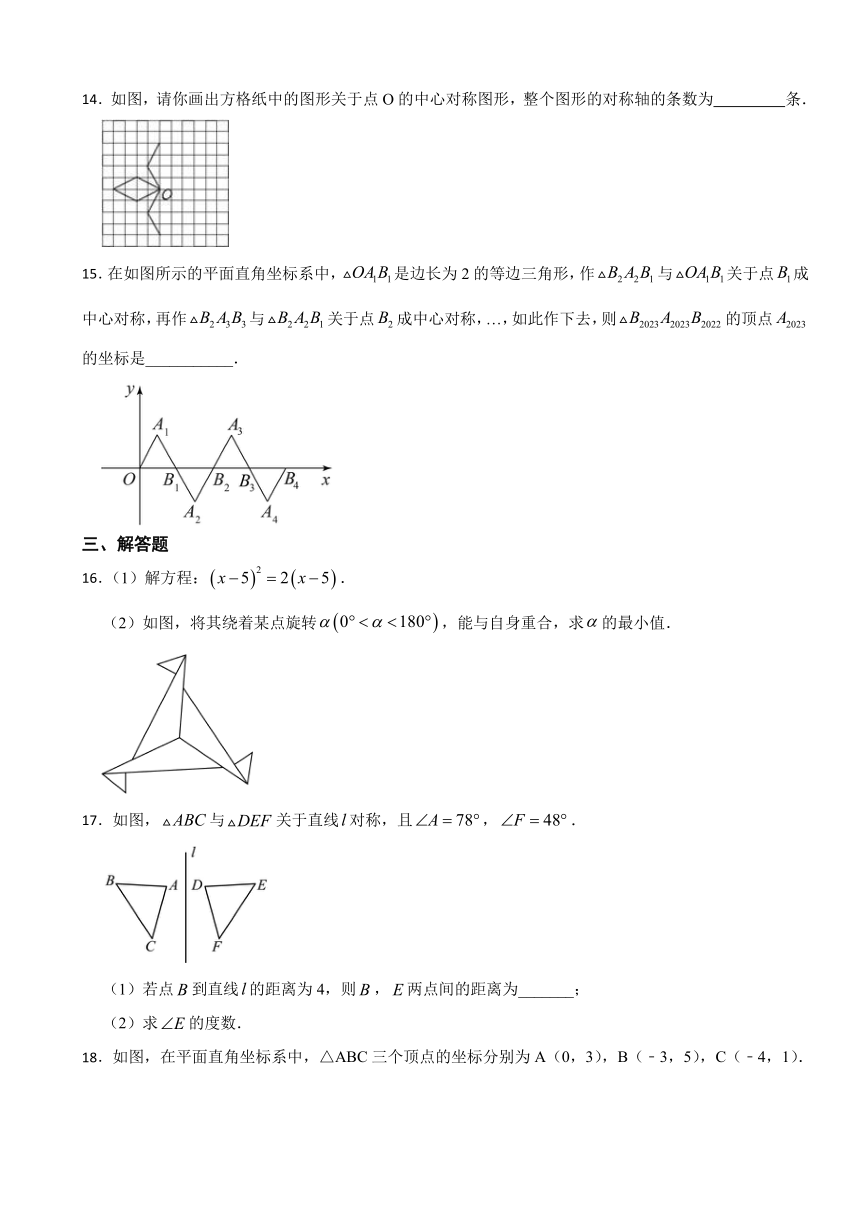
14.如图,请你画出方格纸中的图形关于点O的中心对称图形,整个图形的对称轴的条数为 条.
15.在如图所示的平面直角坐标系中,是边长为2的等边三角形,作与关于点成中心对称,再作与关于点成中心对称,…,如此作下去,则的顶点的坐标是___________.
三、解答题
16.(1)解方程:.
(2)如图,将其绕着某点旋转,能与自身重合,求的最小值.
17.如图,与关于直线对称,且,.
(1)若点到直线的距离为4,则,两点间的距离为_______;
(2)求的度数.
18.如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,3),B(﹣3,5),C(﹣4,1).
①把△ABC向右平移2个单位得△A1B1C1,请画出△A1B1C1,并写出点A1的坐标;
②把△ABC绕原点O旋转180°得到△A2B2C2,请画出△A2B2C2.
19.如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线AB平移至△FEG,DE、FG相交于点H.判断线段DE、FG的位置关系,并说明理由.
20.在平面直角坐标系中,△ABC的三个顶点在格点上(每个方格的边长均为1个单位长度).
⑴请画出△ABC关于原点对称的图形△A1B1C1,并写出B1点的坐标.
⑵将△ABC绕点B逆时针旋转90°,画出旋转后得到的△A2B2C2;
⑶求(2)中点A移动的距离.
21.如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=2.Rt△AB′C′可以看作是由Rt△ABC绕A点逆时针方向旋转60°得到的,求线段 B′C的长.
22.如图所示,把△ABC绕点A旋转至△ADE位置,延长BC交AD于F,交DE于G,若∠CAD=10°,∠D=25°,∠EAB=120°,求∠DFB的度数.
23.如图1,如图,已知直线经过、两点,若.
(1)求的值;
(2)如图2,若是线段上一点,将线段绕点顺时针旋转得到(即),此时点恰好落在直线上.
①求点和点的坐标;
②直线关于轴对称的直线交轴于点,若点在直线上,在直线上,是否存在以、、、为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点的坐标,若不存在,请说明理由.
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】A
4.【答案】C
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】B
10.【答案】B
11.【答案】
12.【答案】
13.【答案】(2,﹣3)
14.【答案】4
15.【答案】
16.【答案】(1),;(2)
17.【答案】(1)
(2)
18.【答案】解:①△A1B1C1如图所示,点A1(2,3);
②△A2B2C2如图所示.
19.【答案】解:DE⊥FG.
理由:由题知:Rt△ABC≌Rt△BDE≌Rt△FEG
∴∠A=∠BDE=∠GFE
∵∠BDE+∠BED=90°
∴∠GFE+∠BED=90°,即DE⊥FG
20.【答案】解:⑴如图,△A1B1C1即为所求,B1点的坐标(-4,-2);
⑵如图,△A2B2C2;即为所求;
⑶∵AB==
∴点A移动的距离==π.
21.【答案】解:如图,作B′E⊥AC交CA的延长线于E,
∵∠ACB=90°,∠BAC=60°,AB=2, ∴∠ABC=30°, ∴AC= AB=1,
∵Rt△AB′C′可以看作是由Rt△ABC绕点A逆时针方向旋转60°得到的,
∴AB=AB′=2,∠B′AB=60°, ∴∠EAB′=180°﹣∠B′AB﹣∠BAC=60°, ∵B′E⊥EC, ∴∠AB′E=30°,
∴AE=1, 在Rt△AB′E中,∵AE=1,AB′=2, ∴B′E= = , ∴EC=AE+AC=2,
在Rt△CEB′中,∵B′E= ,CE=2, ∴B′C= = .
22.【答案】解:由旋转可知:△ABC≌△ADE,
∴∠B=∠D=25°,∠EAD=∠CAB,
∵∠EAB=∠EAD+∠CAD+∠CAB=120°,∠CAD=10°,
∴∠CAB=(120°﹣10°)÷2=55°,
∴∠FAB=∠CAB+∠CAD=55°+10°=65°,
∵∠DFB是△ABF的外角,
∴∠DFB=∠B+∠FAB,
∴∠DFB=25°+65°=90°.
23.【答案】(1)
(2)①点,点;②存在,点坐标为或或
一、单选题
1.在下列图案中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.如图,将绕点逆时针旋转到,点恰好落在边上,已知,则的长为( )
A. B. C. D.
3.如图,将绕点逆时针旋转后得到,点,的对应点分别为,,点恰好在边上,且点在的延长线上,连接,若,则下列结论一定正确的是( )
A. B.
C.旋转角是 D.
4.如图, 在中, , 以点为中心逆时针旋转得到, 点, 的对应点分别是点, , 且平分, 交于点, 则下列结论一定正确的是( )
A. B.
C. D.
5. 下面的图形中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
6.如图,在△ABC中,∠BAC=102°,将△ABC绕点A按逆时针方向旋转得到.若点恰好落在BC边上,且,则的度数为( )
A.24° B.26° C.28° D.30°
7.如图所示的图案是由六个全等的菱形拼成的,它也可以看作是以一个图案为“基本图案”,通过旋转得到的.以下图案中,不能作为“基本图案”的一个是( )
A.A B.B C.C D.D
8.已知点 , 是坐标原点,将线段 绕点 逆时针旋转 ,点 旋转后的对应点 ,则点 的坐标是( )
A. B. C. D.
9.如图,正方形的对角线交于点O,将绕点B顺时针旋转,得到,连接,过A作于点F.若,则( )
A. B. C. D.
10.如图,边长为9的等边三角形ABC中,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是( )
A.3 B. C. D.
二、填空题
11.如图,将绕点顺时针旋转得到,若点恰好在的延长线上,,则的度数为
12.如图,四边形ABCD是边长为7的正方形,点E在边AD上,连接CE,将CE绕点E逆时针旋转90°得到EF,连接BF,若,则 .
13.在平面直角坐标系中,点(﹣2,3)关于原点对称的点的坐标是 .
14.如图,请你画出方格纸中的图形关于点O的中心对称图形,整个图形的对称轴的条数为 条.
15.在如图所示的平面直角坐标系中,是边长为2的等边三角形,作与关于点成中心对称,再作与关于点成中心对称,…,如此作下去,则的顶点的坐标是___________.
三、解答题
16.(1)解方程:.
(2)如图,将其绕着某点旋转,能与自身重合,求的最小值.
17.如图,与关于直线对称,且,.
(1)若点到直线的距离为4,则,两点间的距离为_______;
(2)求的度数.
18.如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,3),B(﹣3,5),C(﹣4,1).
①把△ABC向右平移2个单位得△A1B1C1,请画出△A1B1C1,并写出点A1的坐标;
②把△ABC绕原点O旋转180°得到△A2B2C2,请画出△A2B2C2.
19.如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线AB平移至△FEG,DE、FG相交于点H.判断线段DE、FG的位置关系,并说明理由.
20.在平面直角坐标系中,△ABC的三个顶点在格点上(每个方格的边长均为1个单位长度).
⑴请画出△ABC关于原点对称的图形△A1B1C1,并写出B1点的坐标.
⑵将△ABC绕点B逆时针旋转90°,画出旋转后得到的△A2B2C2;
⑶求(2)中点A移动的距离.
21.如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=2.Rt△AB′C′可以看作是由Rt△ABC绕A点逆时针方向旋转60°得到的,求线段 B′C的长.
22.如图所示,把△ABC绕点A旋转至△ADE位置,延长BC交AD于F,交DE于G,若∠CAD=10°,∠D=25°,∠EAB=120°,求∠DFB的度数.
23.如图1,如图,已知直线经过、两点,若.
(1)求的值;
(2)如图2,若是线段上一点,将线段绕点顺时针旋转得到(即),此时点恰好落在直线上.
①求点和点的坐标;
②直线关于轴对称的直线交轴于点,若点在直线上,在直线上,是否存在以、、、为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点的坐标,若不存在,请说明理由.
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】A
4.【答案】C
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】B
10.【答案】B
11.【答案】
12.【答案】
13.【答案】(2,﹣3)
14.【答案】4
15.【答案】
16.【答案】(1),;(2)
17.【答案】(1)
(2)
18.【答案】解:①△A1B1C1如图所示,点A1(2,3);
②△A2B2C2如图所示.
19.【答案】解:DE⊥FG.
理由:由题知:Rt△ABC≌Rt△BDE≌Rt△FEG
∴∠A=∠BDE=∠GFE
∵∠BDE+∠BED=90°
∴∠GFE+∠BED=90°,即DE⊥FG
20.【答案】解:⑴如图,△A1B1C1即为所求,B1点的坐标(-4,-2);
⑵如图,△A2B2C2;即为所求;
⑶∵AB==
∴点A移动的距离==π.
21.【答案】解:如图,作B′E⊥AC交CA的延长线于E,
∵∠ACB=90°,∠BAC=60°,AB=2, ∴∠ABC=30°, ∴AC= AB=1,
∵Rt△AB′C′可以看作是由Rt△ABC绕点A逆时针方向旋转60°得到的,
∴AB=AB′=2,∠B′AB=60°, ∴∠EAB′=180°﹣∠B′AB﹣∠BAC=60°, ∵B′E⊥EC, ∴∠AB′E=30°,
∴AE=1, 在Rt△AB′E中,∵AE=1,AB′=2, ∴B′E= = , ∴EC=AE+AC=2,
在Rt△CEB′中,∵B′E= ,CE=2, ∴B′C= = .
22.【答案】解:由旋转可知:△ABC≌△ADE,
∴∠B=∠D=25°,∠EAD=∠CAB,
∵∠EAB=∠EAD+∠CAD+∠CAB=120°,∠CAD=10°,
∴∠CAB=(120°﹣10°)÷2=55°,
∴∠FAB=∠CAB+∠CAD=55°+10°=65°,
∵∠DFB是△ABF的外角,
∴∠DFB=∠B+∠FAB,
∴∠DFB=25°+65°=90°.
23.【答案】(1)
(2)①点,点;②存在,点坐标为或或
同课章节目录
