北师大版九年级数学上册 期末综合检测试卷 (含详解)
文档属性
| 名称 | 北师大版九年级数学上册 期末综合检测试卷 (含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 427.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-17 12:20:26 | ||
图片预览




文档简介
北师大版九年级数学上期末综合检测试卷
一、单选题(共10题;共30分)
1. 已知,,且 ,则sinA
与的关系为 ( )
A. B.
C. D. 不确定
2. 如图是有几个相同的小正方体组成的一个几何体.它的左视图是( )
A. B.
C. D.
3. 下列命题中,是真命题的是( )
A. 两条对角线互相平分的四边形是平行四边形
B. 两条对角线相等的四边形是矩形
C. 两条对角线互相垂直四边形是菱形
D. 两条对角线互相垂直且相等的四边形是正方形
4. 用配方法将方程变形,正确的是( )
A. B.
C. D.
5. 如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:①AC=AD;②BD⊥AC;③四边形ACED是菱形.其中正确的个数是( )
A 0 B. 1 C. 2 D. 3
6. 如图所示,设A为反比例函数图象上一点,且的面积为3,则这个反比例函数解析式为
A. B. C. D.
7. 某种商品原价是100元,经两次降价后的价格是90元.设平均每次降价的百分率为x,可列方程为( )
A. 100(1﹣2x)=90 B. 100(1+2x)=90
C. 100(1﹣x)2=90 D. 100(1+x)2=90
8. 方程x2 = 2x的解是( )
A. x=2 B. ,= 0 C. =2,=0 D. x = 0
9. 如图,已知矩形ABCD沿着直线BD折叠,使点C落在C'处,BC'交AD于E,AD=8,AB=4,则DE的长为( )
A. 3 B. 4 C. 5 D. 6
10. 如图,正方形ABCD的边长为4,点E在对角线BD上,且,EF⊥AB,垂足为F,则EF的长为
A 1 B. C. D.
二、填空题(共10题;共30分)
11. 已知关于x的一元二次方程2x2﹣3kx+4=0的一个根是1,则k=_______
12. 一个不透明的袋子中有1个白球、3个黄球和2个红球,这些球除颜色外都相同.将袋子中的球搅拌均匀,从中一次随机摸出两个球都是黄球的概率为________.
13. 一块四周镶有宽度相等的花边的地毯如下图,它的长为8m,宽为5m.地毯中央长方形图案的面积为18m2 , 那么花边有多宽?设花边的宽为x, 则可得方程为________.
14. 如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=4,∠AOD=120°,则对角线AC的长度为________ .
15. 如图,在平面直角坐标系中,二次函数y=ax2+c(a≠0)的图象过正方形ABOC的三个顶点A,B,C,则ac的值是________.
16. 一水塘里有鲤鱼、鲢鱼共10000条,一渔民通过多次捕捞实验后发现,鲤鱼出现的频率为30%,则水塘有鲢鱼 ________ 条.
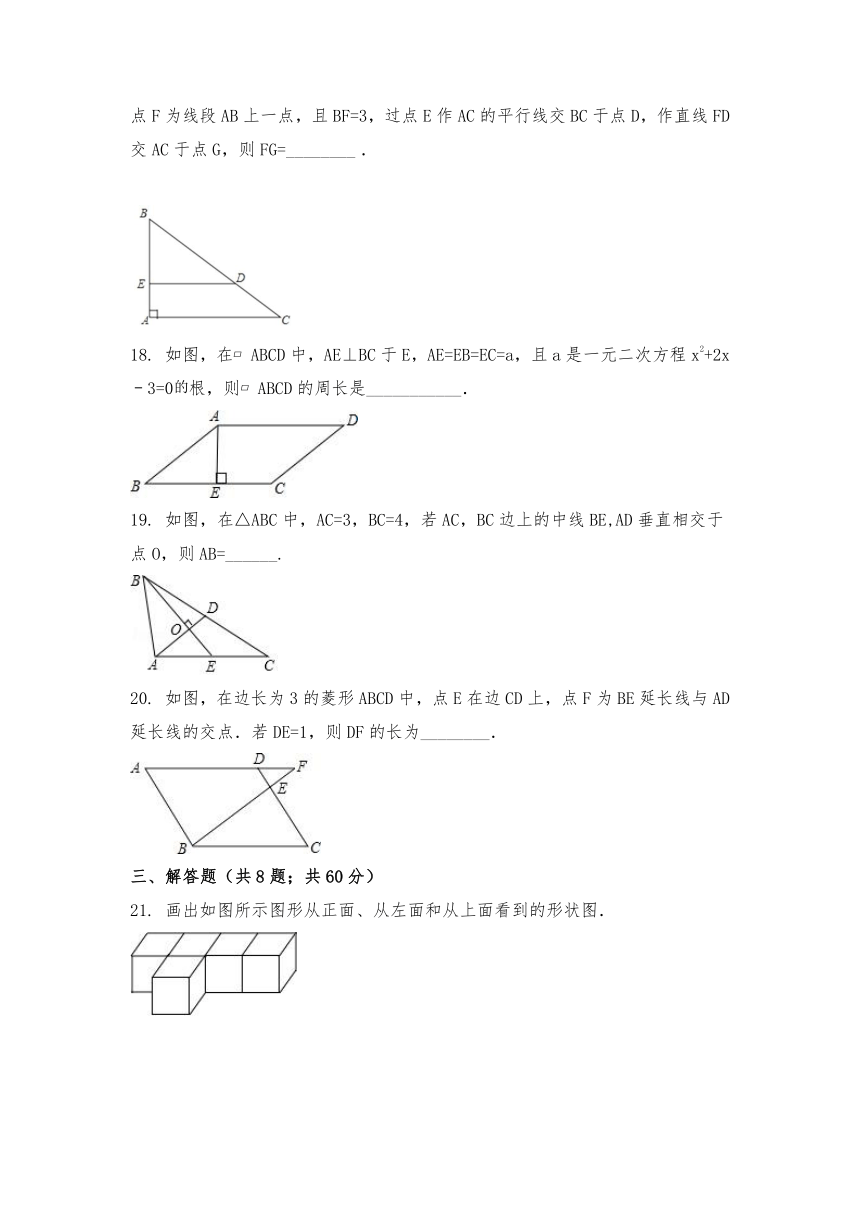
17. 如图,Rt△ABC中,∠A=90°,AB=6,AC=8,点E为边AB上一点,AE=2,点F为线段AB上一点,且BF=3,过点E作AC的平行线交BC于点D,作直线FD交AC于点G,则FG=________ .
18. 如图,在 ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x﹣3=0根,则 ABCD的周长是___________.
19. 如图,在△ABC中,AC=3,BC=4,若AC,BC边上的中线BE,AD垂直相交于点O,则AB=______.
20. 如图,在边长为3的菱形ABCD中,点E在边CD上,点F为BE延长线与AD延长线的交点.若DE=1,则DF的长为________.
三、解答题(共8题;共60分)
21. 画出如图所示图形从正面、从左面和从上面看到的形状图.
22. 有两组牌,每组牌都是4张,牌面数字分别是1,2,3,4,从每组牌中任取一张,求抽取的两张牌的数字之和等于5的概率,并画出树状图.
23. 如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米.某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米,求这个矩形的面积.
24. 如图,邻边不等的矩形花圃ABCD,它的一边AD利用已有的围墙,另外三边所围的栅栏的总长度是6m.若矩形的面积为4m2,求AB的长度.(可利用的围墙长度不超过3m)
25. 在△ABC 中,D 是 BC 边的中点,E、F 分别在 AD 及其延长线上,CE∥BF,连接BE、CF.
(1)求证:△BDF ≌△CDE;
(2)若 DE =BC,试判断四边形 BFCE 是怎样的四边形,并证明你的结论.
26. 一个不透明的袋子里装有红、黄、蓝三种颜色的球(除颜色以外,其余都相同),其中红球2个,黄球2个,从中随机摸出一个球是蓝色球的概率为 .
(1)求袋子里蓝色球的个数;
(2)甲、乙两人分别从袋中摸出一个球(不放回),求摸出两个球中一个是红球一个是黄球的概率.
27. 某工厂拟建一座平面图形为矩形且面积为200平方米的三级污水处理池(平面图如图ABCD所示).由于地形限制,三级污水处理池的长、宽都不能超过16米.如果池的外围墙建造单价为每米400元,中间两条隔墙建造单价为每米300元,池底建造单价为每平方米80元.(池墙的厚度忽略不计)当三级污水处理池的总造价为47200元时,求池长x.
28.在一次课题学习中,老师让同学们合作编题,某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解:
如图,将矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H,使得AE=CG,BF=DH,连接EF,FG,GH,HE.
(1)求证:四边形EFGH为平行四边形;
(2)若矩形ABCD是边长为1的正方形,且∠FEB=45°,tan∠AEH=2,求AE的长.
答案
一、单选题
1. B
【解析】
【分析】根据,可得,再根据三角函数值只与角的大小有关即可求解.
【详解】解:∵,
∴,
∴.
故选:B
2.B
【解析】
【分析】根据左视图是从左面看到的图判定即可.
【详解】解:左面看去得到的正方形第一层是2个正方形,第二层是1个正方形.
故选:B
3.A
【解析】
【分析】根据特殊四边形判定方法进行判断.
【详解】解:对角线互相平分的四边形是平行四边形,故选项A符合题意;
对角线相等的平行四边形是矩形,故选项B不符合题意;
对角线互相垂直的平行四边形是菱形,故选项C不符合题意;
对角线互相垂直且相等的平行四边形是正方形,故选项D不符合题意.
故选:A.
4. D
【解析】
【分析】把常数项-11移项后,应该在左右两边同时加上一次项系数6的一半的平方.
【详解】解:把方程x2+6x-11=0的常数项移到等号的右边,得到x2+6x=11,
方程两边同时加上一次项系数一半的平方,得到x2+6x+9=11+9,
配方得(x+3)2=20.
故选:D.
5. D
【解析】
【详解】试题分析:根据旋转和等边三角形的性质得出∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE,求出△ACD是等边三角形,求出AD=AC,根据菱形的判定得出四边形ABCD和ACED都是菱形,根据菱形的判定推出AC⊥BD. ∵将等边△ABC绕点C顺时针旋转120°得到△EDC, ∴∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE, ∴∠ACD=120°﹣60°=60°, ∴△ACD是等边三角形,
∴AC=AD,AC=AD=DE=CE, ∴四边形ACED是菱形,
∵将等边△ABC绕点C顺时针旋转120°得到△EDC,AC=AD, ∴AB=BC=CD=AD,
∴四边形ABCD是菱形, ∴BD⊥AC,∴①②③都正确
6. D
【解析】
【详解】试题分析:由的面积为3根据反比例函数k的几何意义求解即可.
∵的面积为3,反比例函数的图象有一支在第二象限
∴
故选D.
7. C
【解析】
【详解】试题解析:设该商品平均每次降价的百分率为x,根据降价后的价格=降价前的价格(1-降价的百分率),则第一次降价后的价格是100(1-x),第二次后的价格是100(1-x)2,据此根据题意得:100(1-x)2=90.
故选C.
8. C
【解析】
【分析】先移项得到x2-2x=0,再把方程左边进行因式分解得到x(x-2)=0,方程转化为两个一元一次方程:x=0或x-2=0,即可得到原方程的解为x1=0,x2=2.
【详解】解:∵x2-2x=0,
∴x(x-2)=0,
∴x=0或x-2=0,
∴=2,=0.
故选:C.
9. C
【解析】
【分析】根据折叠前后角相等可知△ABE≌△C'DE,利用勾股定理可求出.
【详解】解:∵四边形ABCD是矩形,
∴AB=CD,∠C=∠A=90°
由折叠的性质可得:C'D=CD=AB;∠C'=∠C=∠A
在△ABE与△C'ED中
∴△ABE≌△C'DE(AAS)
∴DE=BE
设DE=BE=x,则AE=8-x,AB=4,在直角三角形ABE中,由勾股定理得:
解得x=5
故选:C.
10. C
【解析】
【详解】解:在正方形ABCD中,∠ABD=∠ADB=45°,
∵∠BAE=22.5°,∴∠DAE=90°-∠BAE=90°-22.5°=67.5°.
在△ADE中,∠AED=180°-45°-67.5°=67.5°,∴∠DAE=∠ADE.∴AD=DE=4.
∵正方形的边长为4,∴BD=.∴BE=BD-DE=.
∵EF⊥AB,∠ABD=45°,∴△BEF是等腰直角三角形.
∴EF=BE==.
故选:C.
二、填空题
11. k=2.
【解析】
【详解】试题分析:把x=1代入已知方程列出关于k的一元一次方程,通过解方程求得k的值.
试题解析:依题意,得
2×12﹣3k×1+4=0,即2﹣3k+4=0,
解得,k=2.
12.
【解析】
【详解】试题分析:画树形图得:
所以两次都摸到白球的概率==.故答案为.
13. (8-2x)(5-2x)=18
【解析】
【详解】设花边的宽为m,则中央长方形图案的长为m,宽为m,根据题意可得方程:.
14.8
【解析】
【分析】根据矩形的对角线互相平分且相等,可知OA=OB=OC=OD,然后由∠AOD=120°可求得∠AOB=60°,证明△OAB是等边三角形,求出OA=AB=4即可得出答案.
【详解】解:在矩形ABCD中,OA=OB=OC=OD,
∵∠AOD=120°,
∴∠AOB=60°,
∴△OAB是等边三角形,
∴OA=AB=4,
∴AC=2OA=8,
故答案为:8.
15.-2.
【解析】
【分析】设正方形的对角线OA长为2m,根据正方形的性质则可得出B、C坐标,代入二次函数y=ax2+c中,即可求出a和c,从而求积.
【详解】设正方形的对角线OA长为2m,则B(﹣m,m),C(m,m),A(0,2m);
把A,C的坐标代入解析式可得:c=2m①,am2+c=m②,
①代入②得:am2+2m=m,
解得:a=-,
则ac=-2m=-2.
16. 7000
【解析】
【详解】试题分析:∵水塘里有鲤鱼、鲢鱼共10000条,
一渔民通过多次捕捞实验后发现,鲤鱼出现的频率为30%,
∴鲤鱼出现的频率为70%,
∴水塘有鲢鱼有10000×70%=7000条.
故答案是7000.
17.
【解析】
【分析】根据已知条件得到AF=3,EF=1,由DE∥AC,得到△BED~△ABC,根据相似三角形的性质得到,即,求得DE=,通过△DEF~△GAF,得到,于是得到,可得AG=16,根据勾股定理即可得到结论.
【详解】解:如图
AB=6,BF=3,AF=3,
AE=2,EF=1,
DE∥AC
△BED~△ABC,
即:
DE=,
DE∥AC,
ADEF~AGAF,
AG=16,
FG==
故答案为:.
18. 4+2
【解析】
【分析】先解一元二次方程求出a,再使用勾股定理求得AB,从而计算平行四边形的周长.
【详解】解:因为,a是一元二次方程的根,
所以,
即,
解得a=1或a=-3(不符合题意,舍去),
所以AE=EB=EC=a=1,
在Rt△ABE中,AB=,
所以,BC=EB+EC=2,
所以,□ABCD的周长=2(AB+BC)
=2.
【点睛】
【解析】
【分析】利用三角形中线定义得到BD=2,AE=,且可判定点O为△ABC的重心,所以AO=2OD,OB=2OE,利用勾股定理得到BO2+OD2=4,OE2+AO2=,等量代换得到BO2+ AO2=4,BO2+AO2=,把两式相加得到BO2+AO2=5,然后再利用勾股定理可计算出AB的长.
【详解】解:∵AD、BE为AC,BC边上的中线,
∴BD=BC=2,AE=AC=,点O为△ABC的重心,
∴AO=2OD,OB=2OE,
∵BE⊥AD,
∴BO2+OD2=BD2=4,OE2+AO2=AE2=,
∴BO2+AO2=4,BO2+AO2=,
∴BO2+AO2= ,
∴BO2+AO2=5,
∴AB==.
故答案是:.
20. 1.5
【解析】
【分析】求出EC,根据菱形的性质得出AD∥BC,得出相似三角形,根据相似三角形的性质得出比例式,代入求出即可.
【详解】∵DE=1,DC=3,
∴EC=3-1=2,
∵四边形ABCD是菱形,
∴AD∥BC,
∴△DEF∽△CEB,
∴,
∴,
∴DF=1.5,
故答案为1.5.
三、解答题
21.如图所示:
22. 解:如图,
共有16种等可能的情况,和为5的情况有4种,
∴P(和为5)= .
23. 如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米.某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米,求这个矩形的面积.
【答案】2000或1920
【解析】
【分析】利用矩形的性质得出△ADG∽△ABC,然后利用相似三角形对应高的比等于相似比求出矩形的长,然后利用矩形的面积公式计算即可.
【详解】∵矩形DEFG中DG∥EF,∴∠ADG=∠B,∠AGD=∠C,∴△ADG∽△ABC,∴.
①若DE为宽,则,∴DG=50,此时矩形的面积是:50×40=2000平方米;
②若DG为宽,则,∴DE=48,此时矩形的面积是:48×40=1920平方米.
24. 解:设m,则 m . ………1分
根据题意可得, . ………2分
解得 ………4分
答:AB的长为1 m.
【解析】
【详解】试题分析:设垂直墙的篱笆的长为x,那么平行墙的篱笆长为(6-2x),(6-2x)和x就是鸡场的长和宽.然后用面积做等量关系可列方程求解.
试题解析:设AB长为x米,则BC长为(6-2x)米.
依题意,得x(6-2x)=4.
整理,得x2-3x+2=0.
解方程,得x1=1,x2=2.
所以当x=1时,6-2x=4;
当x=2时,6-2x=2(舍去).
答:AB的长为1米.
25. 在△ABC 中,D 是 BC 边的中点,E、F 分别在 AD 及其延长线上,CE∥BF,连接BE、CF.
(1)求证:△BDF ≌△CDE;
(2)解:(1)∵CE∥BF,
∴∠CED=∠BFD.
∵D是BC边的中点,
∴BD=DC,
在△BDF和△CDE中, ,
∴△BDF≌△CDE(AAS).
(2)四边形BFCE是矩形.理由如下:
∵△BDF≌△CDE,
∴DE=DF,
又∵BD=DC,
∴四边形BFCE是平行四边形.
∵DE=BC,DE=EF,
∴BC=EF,
∴平行四边形BFCE是矩形.
26.(1)设袋子里蓝色球个数为x,
根据题意得:,
解得:x=1,
答:袋子里蓝色球的个数为1;
(2)画树状图如下:
由树状图可知:所有可能出现的结果共有20种,符合题意的结果有8种,
∴P(一个是红球一个是黄球)==,
答:摸出的两个球中一个是红球一个是黄球的概率为.
27. 根据题意,得2(x+×400)+2××300+200×80=47200,
整理,得﹣39x+350=0,
解得=25,=14,
∵x=25>16,
∴x=25不合题意,舍去.
∵x=14<16,=<16,
∴x=14符合题意.
所以,池长为14米.
28. 解:(1)证明:∵四边形ABCD是矩形,∴AD=BC,∠BAD=∠BCD=90°,
∵BF=DH,
∴AH=CF,
在Rt△AEH中,EH=,
在Rt△CFG中,FG=,
∵AE=CG,
∴EH=FG,
同理:EF=HG,
∴四边形EFGH为平行四边形;
(2)解:在正方形ABCD中,AB=AD=1,
设AE=x,则BE=x+1,
在Rt△BEF中,∠BEF=45°,
∴BE=BF,
∵BF=DH,
∴DH=BE=x+1,
∴AH=AD+DH=x+2,
在Rtt△AEH中,tan∠AEH=2,
∴AH=2AE,
∴2+x=2x,
解得:x=2,
AE=2.
一、单选题(共10题;共30分)
1. 已知,,且 ,则sinA
与的关系为 ( )
A. B.
C. D. 不确定
2. 如图是有几个相同的小正方体组成的一个几何体.它的左视图是( )
A. B.
C. D.
3. 下列命题中,是真命题的是( )
A. 两条对角线互相平分的四边形是平行四边形
B. 两条对角线相等的四边形是矩形
C. 两条对角线互相垂直四边形是菱形
D. 两条对角线互相垂直且相等的四边形是正方形
4. 用配方法将方程变形,正确的是( )
A. B.
C. D.
5. 如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:①AC=AD;②BD⊥AC;③四边形ACED是菱形.其中正确的个数是( )
A 0 B. 1 C. 2 D. 3
6. 如图所示,设A为反比例函数图象上一点,且的面积为3,则这个反比例函数解析式为
A. B. C. D.
7. 某种商品原价是100元,经两次降价后的价格是90元.设平均每次降价的百分率为x,可列方程为( )
A. 100(1﹣2x)=90 B. 100(1+2x)=90
C. 100(1﹣x)2=90 D. 100(1+x)2=90
8. 方程x2 = 2x的解是( )
A. x=2 B. ,= 0 C. =2,=0 D. x = 0
9. 如图,已知矩形ABCD沿着直线BD折叠,使点C落在C'处,BC'交AD于E,AD=8,AB=4,则DE的长为( )
A. 3 B. 4 C. 5 D. 6
10. 如图,正方形ABCD的边长为4,点E在对角线BD上,且,EF⊥AB,垂足为F,则EF的长为
A 1 B. C. D.
二、填空题(共10题;共30分)
11. 已知关于x的一元二次方程2x2﹣3kx+4=0的一个根是1,则k=_______
12. 一个不透明的袋子中有1个白球、3个黄球和2个红球,这些球除颜色外都相同.将袋子中的球搅拌均匀,从中一次随机摸出两个球都是黄球的概率为________.
13. 一块四周镶有宽度相等的花边的地毯如下图,它的长为8m,宽为5m.地毯中央长方形图案的面积为18m2 , 那么花边有多宽?设花边的宽为x, 则可得方程为________.
14. 如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=4,∠AOD=120°,则对角线AC的长度为________ .
15. 如图,在平面直角坐标系中,二次函数y=ax2+c(a≠0)的图象过正方形ABOC的三个顶点A,B,C,则ac的值是________.
16. 一水塘里有鲤鱼、鲢鱼共10000条,一渔民通过多次捕捞实验后发现,鲤鱼出现的频率为30%,则水塘有鲢鱼 ________ 条.
17. 如图,Rt△ABC中,∠A=90°,AB=6,AC=8,点E为边AB上一点,AE=2,点F为线段AB上一点,且BF=3,过点E作AC的平行线交BC于点D,作直线FD交AC于点G,则FG=________ .
18. 如图,在 ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x﹣3=0根,则 ABCD的周长是___________.
19. 如图,在△ABC中,AC=3,BC=4,若AC,BC边上的中线BE,AD垂直相交于点O,则AB=______.
20. 如图,在边长为3的菱形ABCD中,点E在边CD上,点F为BE延长线与AD延长线的交点.若DE=1,则DF的长为________.
三、解答题(共8题;共60分)
21. 画出如图所示图形从正面、从左面和从上面看到的形状图.
22. 有两组牌,每组牌都是4张,牌面数字分别是1,2,3,4,从每组牌中任取一张,求抽取的两张牌的数字之和等于5的概率,并画出树状图.
23. 如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米.某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米,求这个矩形的面积.
24. 如图,邻边不等的矩形花圃ABCD,它的一边AD利用已有的围墙,另外三边所围的栅栏的总长度是6m.若矩形的面积为4m2,求AB的长度.(可利用的围墙长度不超过3m)
25. 在△ABC 中,D 是 BC 边的中点,E、F 分别在 AD 及其延长线上,CE∥BF,连接BE、CF.
(1)求证:△BDF ≌△CDE;
(2)若 DE =BC,试判断四边形 BFCE 是怎样的四边形,并证明你的结论.
26. 一个不透明的袋子里装有红、黄、蓝三种颜色的球(除颜色以外,其余都相同),其中红球2个,黄球2个,从中随机摸出一个球是蓝色球的概率为 .
(1)求袋子里蓝色球的个数;
(2)甲、乙两人分别从袋中摸出一个球(不放回),求摸出两个球中一个是红球一个是黄球的概率.
27. 某工厂拟建一座平面图形为矩形且面积为200平方米的三级污水处理池(平面图如图ABCD所示).由于地形限制,三级污水处理池的长、宽都不能超过16米.如果池的外围墙建造单价为每米400元,中间两条隔墙建造单价为每米300元,池底建造单价为每平方米80元.(池墙的厚度忽略不计)当三级污水处理池的总造价为47200元时,求池长x.
28.在一次课题学习中,老师让同学们合作编题,某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解:
如图,将矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H,使得AE=CG,BF=DH,连接EF,FG,GH,HE.
(1)求证:四边形EFGH为平行四边形;
(2)若矩形ABCD是边长为1的正方形,且∠FEB=45°,tan∠AEH=2,求AE的长.
答案
一、单选题
1. B
【解析】
【分析】根据,可得,再根据三角函数值只与角的大小有关即可求解.
【详解】解:∵,
∴,
∴.
故选:B
2.B
【解析】
【分析】根据左视图是从左面看到的图判定即可.
【详解】解:左面看去得到的正方形第一层是2个正方形,第二层是1个正方形.
故选:B
3.A
【解析】
【分析】根据特殊四边形判定方法进行判断.
【详解】解:对角线互相平分的四边形是平行四边形,故选项A符合题意;
对角线相等的平行四边形是矩形,故选项B不符合题意;
对角线互相垂直的平行四边形是菱形,故选项C不符合题意;
对角线互相垂直且相等的平行四边形是正方形,故选项D不符合题意.
故选:A.
4. D
【解析】
【分析】把常数项-11移项后,应该在左右两边同时加上一次项系数6的一半的平方.
【详解】解:把方程x2+6x-11=0的常数项移到等号的右边,得到x2+6x=11,
方程两边同时加上一次项系数一半的平方,得到x2+6x+9=11+9,
配方得(x+3)2=20.
故选:D.
5. D
【解析】
【详解】试题分析:根据旋转和等边三角形的性质得出∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE,求出△ACD是等边三角形,求出AD=AC,根据菱形的判定得出四边形ABCD和ACED都是菱形,根据菱形的判定推出AC⊥BD. ∵将等边△ABC绕点C顺时针旋转120°得到△EDC, ∴∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE, ∴∠ACD=120°﹣60°=60°, ∴△ACD是等边三角形,
∴AC=AD,AC=AD=DE=CE, ∴四边形ACED是菱形,
∵将等边△ABC绕点C顺时针旋转120°得到△EDC,AC=AD, ∴AB=BC=CD=AD,
∴四边形ABCD是菱形, ∴BD⊥AC,∴①②③都正确
6. D
【解析】
【详解】试题分析:由的面积为3根据反比例函数k的几何意义求解即可.
∵的面积为3,反比例函数的图象有一支在第二象限
∴
故选D.
7. C
【解析】
【详解】试题解析:设该商品平均每次降价的百分率为x,根据降价后的价格=降价前的价格(1-降价的百分率),则第一次降价后的价格是100(1-x),第二次后的价格是100(1-x)2,据此根据题意得:100(1-x)2=90.
故选C.
8. C
【解析】
【分析】先移项得到x2-2x=0,再把方程左边进行因式分解得到x(x-2)=0,方程转化为两个一元一次方程:x=0或x-2=0,即可得到原方程的解为x1=0,x2=2.
【详解】解:∵x2-2x=0,
∴x(x-2)=0,
∴x=0或x-2=0,
∴=2,=0.
故选:C.
9. C
【解析】
【分析】根据折叠前后角相等可知△ABE≌△C'DE,利用勾股定理可求出.
【详解】解:∵四边形ABCD是矩形,
∴AB=CD,∠C=∠A=90°
由折叠的性质可得:C'D=CD=AB;∠C'=∠C=∠A
在△ABE与△C'ED中
∴△ABE≌△C'DE(AAS)
∴DE=BE
设DE=BE=x,则AE=8-x,AB=4,在直角三角形ABE中,由勾股定理得:
解得x=5
故选:C.
10. C
【解析】
【详解】解:在正方形ABCD中,∠ABD=∠ADB=45°,
∵∠BAE=22.5°,∴∠DAE=90°-∠BAE=90°-22.5°=67.5°.
在△ADE中,∠AED=180°-45°-67.5°=67.5°,∴∠DAE=∠ADE.∴AD=DE=4.
∵正方形的边长为4,∴BD=.∴BE=BD-DE=.
∵EF⊥AB,∠ABD=45°,∴△BEF是等腰直角三角形.
∴EF=BE==.
故选:C.
二、填空题
11. k=2.
【解析】
【详解】试题分析:把x=1代入已知方程列出关于k的一元一次方程,通过解方程求得k的值.
试题解析:依题意,得
2×12﹣3k×1+4=0,即2﹣3k+4=0,
解得,k=2.
12.
【解析】
【详解】试题分析:画树形图得:
所以两次都摸到白球的概率==.故答案为.
13. (8-2x)(5-2x)=18
【解析】
【详解】设花边的宽为m,则中央长方形图案的长为m,宽为m,根据题意可得方程:.
14.8
【解析】
【分析】根据矩形的对角线互相平分且相等,可知OA=OB=OC=OD,然后由∠AOD=120°可求得∠AOB=60°,证明△OAB是等边三角形,求出OA=AB=4即可得出答案.
【详解】解:在矩形ABCD中,OA=OB=OC=OD,
∵∠AOD=120°,
∴∠AOB=60°,
∴△OAB是等边三角形,
∴OA=AB=4,
∴AC=2OA=8,
故答案为:8.
15.-2.
【解析】
【分析】设正方形的对角线OA长为2m,根据正方形的性质则可得出B、C坐标,代入二次函数y=ax2+c中,即可求出a和c,从而求积.
【详解】设正方形的对角线OA长为2m,则B(﹣m,m),C(m,m),A(0,2m);
把A,C的坐标代入解析式可得:c=2m①,am2+c=m②,
①代入②得:am2+2m=m,
解得:a=-,
则ac=-2m=-2.
16. 7000
【解析】
【详解】试题分析:∵水塘里有鲤鱼、鲢鱼共10000条,
一渔民通过多次捕捞实验后发现,鲤鱼出现的频率为30%,
∴鲤鱼出现的频率为70%,
∴水塘有鲢鱼有10000×70%=7000条.
故答案是7000.
17.
【解析】
【分析】根据已知条件得到AF=3,EF=1,由DE∥AC,得到△BED~△ABC,根据相似三角形的性质得到,即,求得DE=,通过△DEF~△GAF,得到,于是得到,可得AG=16,根据勾股定理即可得到结论.
【详解】解:如图
AB=6,BF=3,AF=3,
AE=2,EF=1,
DE∥AC
△BED~△ABC,
即:
DE=,
DE∥AC,
ADEF~AGAF,
AG=16,
FG==
故答案为:.
18. 4+2
【解析】
【分析】先解一元二次方程求出a,再使用勾股定理求得AB,从而计算平行四边形的周长.
【详解】解:因为,a是一元二次方程的根,
所以,
即,
解得a=1或a=-3(不符合题意,舍去),
所以AE=EB=EC=a=1,
在Rt△ABE中,AB=,
所以,BC=EB+EC=2,
所以,□ABCD的周长=2(AB+BC)
=2.
【点睛】
【解析】
【分析】利用三角形中线定义得到BD=2,AE=,且可判定点O为△ABC的重心,所以AO=2OD,OB=2OE,利用勾股定理得到BO2+OD2=4,OE2+AO2=,等量代换得到BO2+ AO2=4,BO2+AO2=,把两式相加得到BO2+AO2=5,然后再利用勾股定理可计算出AB的长.
【详解】解:∵AD、BE为AC,BC边上的中线,
∴BD=BC=2,AE=AC=,点O为△ABC的重心,
∴AO=2OD,OB=2OE,
∵BE⊥AD,
∴BO2+OD2=BD2=4,OE2+AO2=AE2=,
∴BO2+AO2=4,BO2+AO2=,
∴BO2+AO2= ,
∴BO2+AO2=5,
∴AB==.
故答案是:.
20. 1.5
【解析】
【分析】求出EC,根据菱形的性质得出AD∥BC,得出相似三角形,根据相似三角形的性质得出比例式,代入求出即可.
【详解】∵DE=1,DC=3,
∴EC=3-1=2,
∵四边形ABCD是菱形,
∴AD∥BC,
∴△DEF∽△CEB,
∴,
∴,
∴DF=1.5,
故答案为1.5.
三、解答题
21.如图所示:
22. 解:如图,
共有16种等可能的情况,和为5的情况有4种,
∴P(和为5)= .
23. 如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米.某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米,求这个矩形的面积.
【答案】2000或1920
【解析】
【分析】利用矩形的性质得出△ADG∽△ABC,然后利用相似三角形对应高的比等于相似比求出矩形的长,然后利用矩形的面积公式计算即可.
【详解】∵矩形DEFG中DG∥EF,∴∠ADG=∠B,∠AGD=∠C,∴△ADG∽△ABC,∴.
①若DE为宽,则,∴DG=50,此时矩形的面积是:50×40=2000平方米;
②若DG为宽,则,∴DE=48,此时矩形的面积是:48×40=1920平方米.
24. 解:设m,则 m . ………1分
根据题意可得, . ………2分
解得 ………4分
答:AB的长为1 m.
【解析】
【详解】试题分析:设垂直墙的篱笆的长为x,那么平行墙的篱笆长为(6-2x),(6-2x)和x就是鸡场的长和宽.然后用面积做等量关系可列方程求解.
试题解析:设AB长为x米,则BC长为(6-2x)米.
依题意,得x(6-2x)=4.
整理,得x2-3x+2=0.
解方程,得x1=1,x2=2.
所以当x=1时,6-2x=4;
当x=2时,6-2x=2(舍去).
答:AB的长为1米.
25. 在△ABC 中,D 是 BC 边的中点,E、F 分别在 AD 及其延长线上,CE∥BF,连接BE、CF.
(1)求证:△BDF ≌△CDE;
(2)解:(1)∵CE∥BF,
∴∠CED=∠BFD.
∵D是BC边的中点,
∴BD=DC,
在△BDF和△CDE中, ,
∴△BDF≌△CDE(AAS).
(2)四边形BFCE是矩形.理由如下:
∵△BDF≌△CDE,
∴DE=DF,
又∵BD=DC,
∴四边形BFCE是平行四边形.
∵DE=BC,DE=EF,
∴BC=EF,
∴平行四边形BFCE是矩形.
26.(1)设袋子里蓝色球个数为x,
根据题意得:,
解得:x=1,
答:袋子里蓝色球的个数为1;
(2)画树状图如下:
由树状图可知:所有可能出现的结果共有20种,符合题意的结果有8种,
∴P(一个是红球一个是黄球)==,
答:摸出的两个球中一个是红球一个是黄球的概率为.
27. 根据题意,得2(x+×400)+2××300+200×80=47200,
整理,得﹣39x+350=0,
解得=25,=14,
∵x=25>16,
∴x=25不合题意,舍去.
∵x=14<16,=<16,
∴x=14符合题意.
所以,池长为14米.
28. 解:(1)证明:∵四边形ABCD是矩形,∴AD=BC,∠BAD=∠BCD=90°,
∵BF=DH,
∴AH=CF,
在Rt△AEH中,EH=,
在Rt△CFG中,FG=,
∵AE=CG,
∴EH=FG,
同理:EF=HG,
∴四边形EFGH为平行四边形;
(2)解:在正方形ABCD中,AB=AD=1,
设AE=x,则BE=x+1,
在Rt△BEF中,∠BEF=45°,
∴BE=BF,
∵BF=DH,
∴DH=BE=x+1,
∴AH=AD+DH=x+2,
在Rtt△AEH中,tan∠AEH=2,
∴AH=2AE,
∴2+x=2x,
解得:x=2,
AE=2.
同课章节目录
