2025年中考数学高频考点突破--角度问题(二次函数综合)(含简单答案)
文档属性
| 名称 | 2025年中考数学高频考点突破--角度问题(二次函数综合)(含简单答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 698.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-17 13:06:47 | ||
图片预览

文档简介
2025年中考数学高频考点突破--
角度问题(二次函数综合)
1.如图,在平面直角坐标系xOy中,抛物线y=ax2-2x+c与x轴交于点A和点B(1,0),与y轴相交于点C(0,3).
(1)求抛物线的解析式和顶点D的坐标;
(2)找出图中与∠DAB相等的一个角,并证明;
(3)若点P是第二象限内抛物线上的一点,当点P到直线AC的距离最大时,求点P的坐标.
2.如图,抛物线y=x2+bx+c与x轴交于点A和点B,交y轴于点C.已知A(﹣3,0),C(0,﹣3),抛物线的顶点为点D.请解答下列问题:
(1)求抛物线的解析式,直接写出顶点D的坐标.
(2)P是抛物线上的一动点,当∠PBO=∠CAO时,则点P的坐标为 .
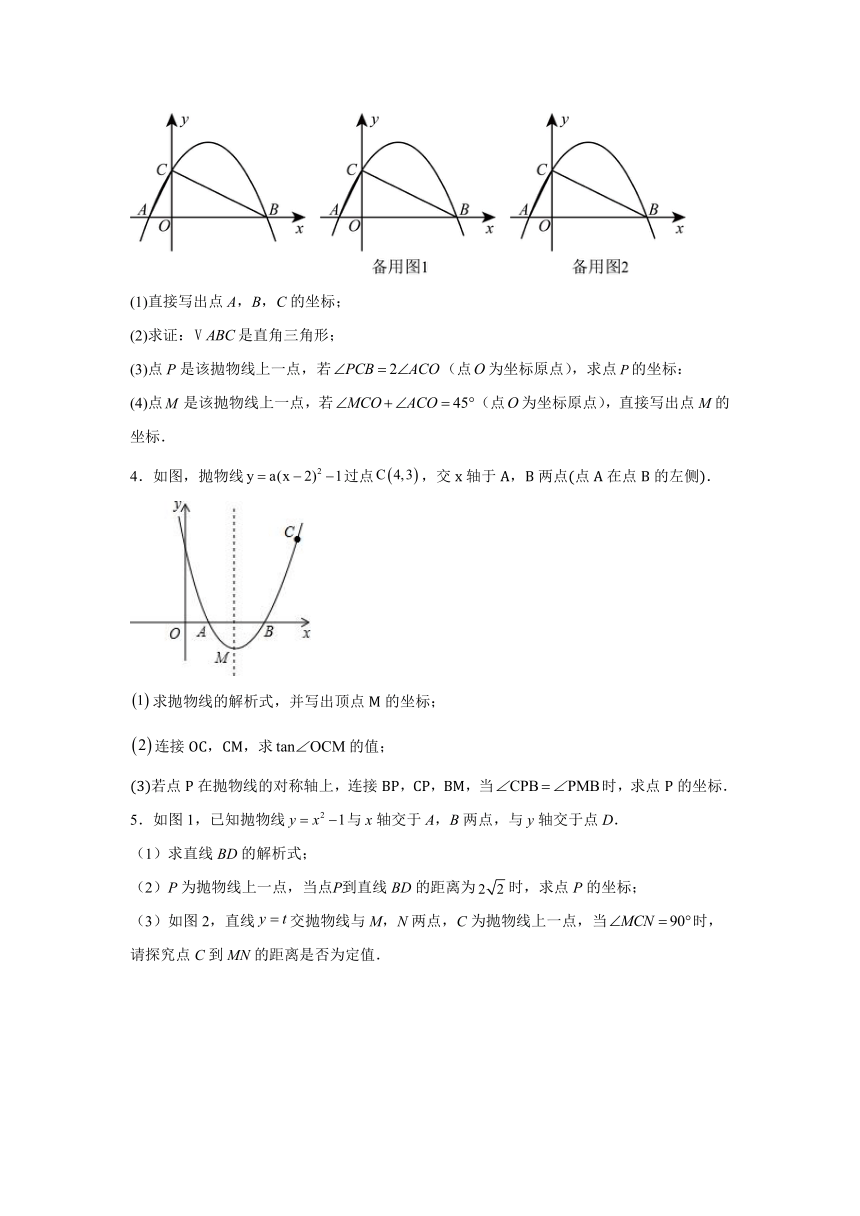
3.如图,二次函数的图像与轴交于点A,B(点A在点的左侧),与轴交于点,连接,.
(1)直接写出点A,B,C的坐标;
(2)求证:是直角三角形;
(3)点P是该拋物线上一点,若(点为坐标原点),求点的坐标:
(4)点是该抛物线上一点,若(点为坐标原点),直接写出点M的坐标.
4.如图,抛物线过点,交x轴于A,B两点点A在点B的左侧.
求抛物线的解析式,并写出顶点M的坐标;
连接OC,CM,求的值;
若点P在抛物线的对称轴上,连接BP,CP,BM,当时,求点P的坐标.
5.如图1,已知抛物线与x轴交于A,B两点,与y轴交于点D.
(1)求直线BD的解析式;
(2)P为抛物线上一点,当点Р到直线BD的距离为时,求点P的坐标;
(3)如图2,直线交抛物线与M,N两点,C为抛物线上一点,当时,请探究点C到MN的距离是否为定值.
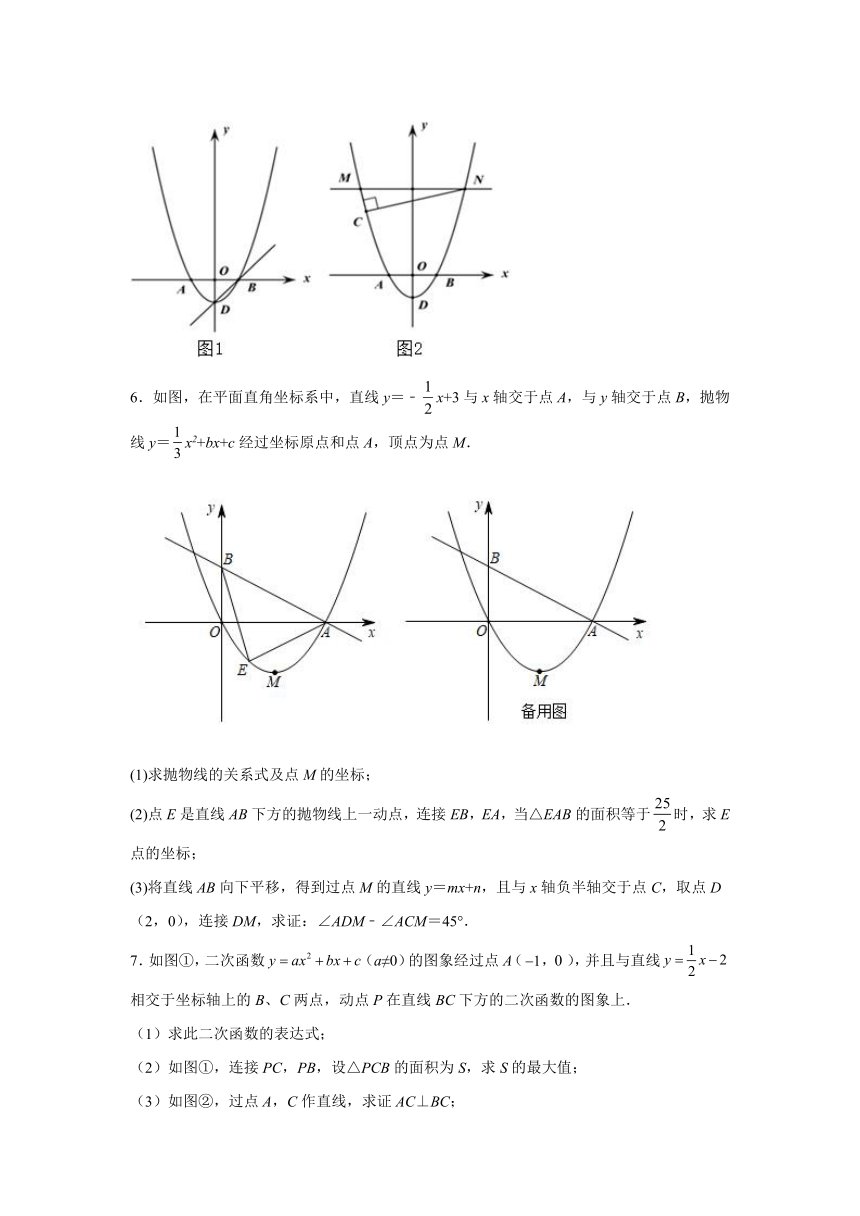
6.如图,在平面直角坐标系中,直线y=﹣x+3与x轴交于点A,与y轴交于点B,抛物线y=x2+bx+c经过坐标原点和点A,顶点为点M.
(1)求抛物线的关系式及点M的坐标;
(2)点E是直线AB下方的抛物线上一动点,连接EB,EA,当△EAB的面积等于时,求E点的坐标;
(3)将直线AB向下平移,得到过点M的直线y=mx+n,且与x轴负半轴交于点C,取点D(2,0),连接DM,求证:∠ADM﹣∠ACM=45°.
7.如图①,二次函数(a≠0)的图象经过点A(,),并且与直线相交于坐标轴上的B、C两点,动点P在直线BC下方的二次函数的图象上.
(1)求此二次函数的表达式;
(2)如图①,连接PC,PB,设△PCB的面积为S,求S的最大值;
(3)如图②,过点A,C作直线,求证AC⊥BC;
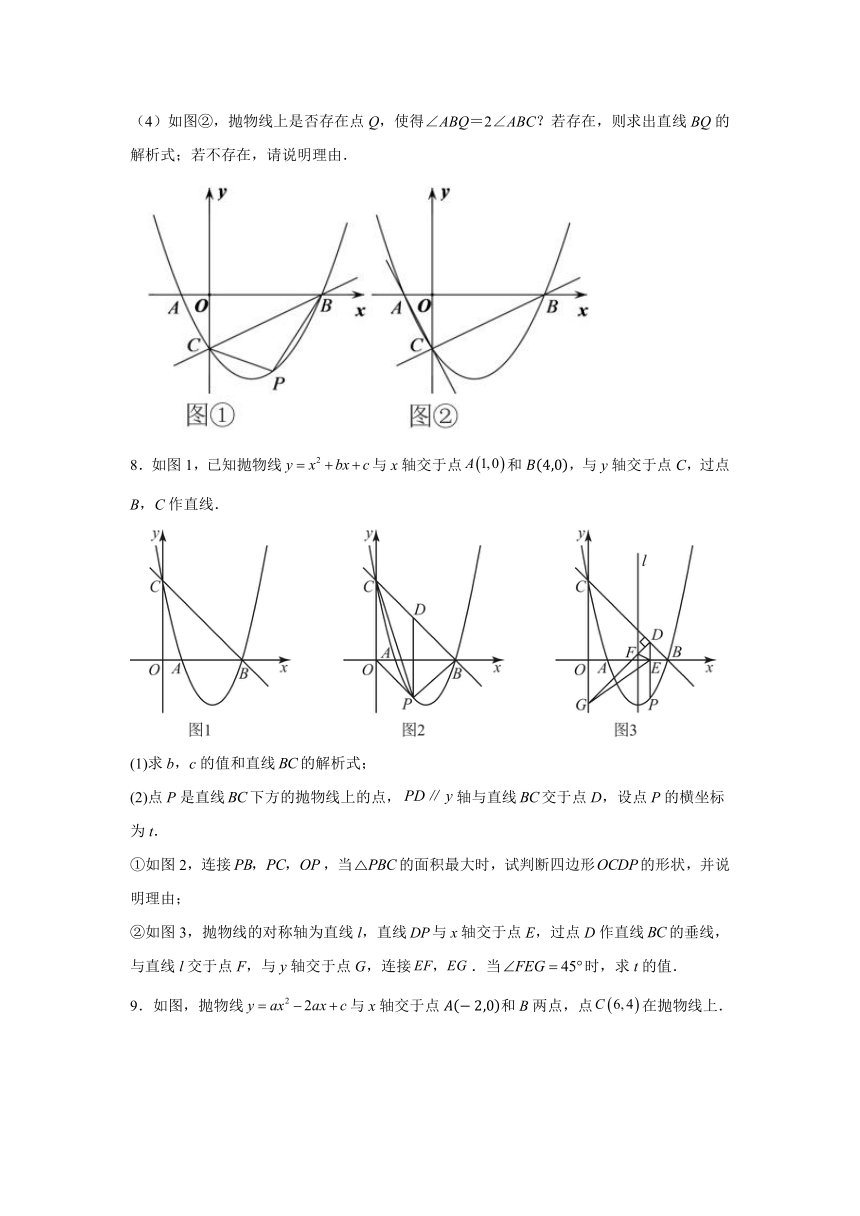
(4)如图②,抛物线上是否存在点Q,使得∠ABQ=2∠ABC?若存在,则求出直线BQ的解析式;若不存在,请说明理由.
8.如图1,已知抛物线与x轴交于点和,与y轴交于点C,过点B,C作直线.
(1)求b,c的值和直线的解析式;
(2)点P是直线下方的抛物线上的点,轴与直线交于点D,设点P的横坐标为t.
①如图2,连接,当的面积最大时,试判断四边形的形状,并说明理由;
②如图3,抛物线的对称轴为直线l,直线与x轴交于点E,过点D作直线的垂线,与直线l交于点F,与y轴交于点G,连接.当时,求t的值.
9.如图,抛物线与x轴交于点和B两点,点在抛物线上.
(1)直接写出B点坐标:_________________,抛物线解析式为_________________(一般式);
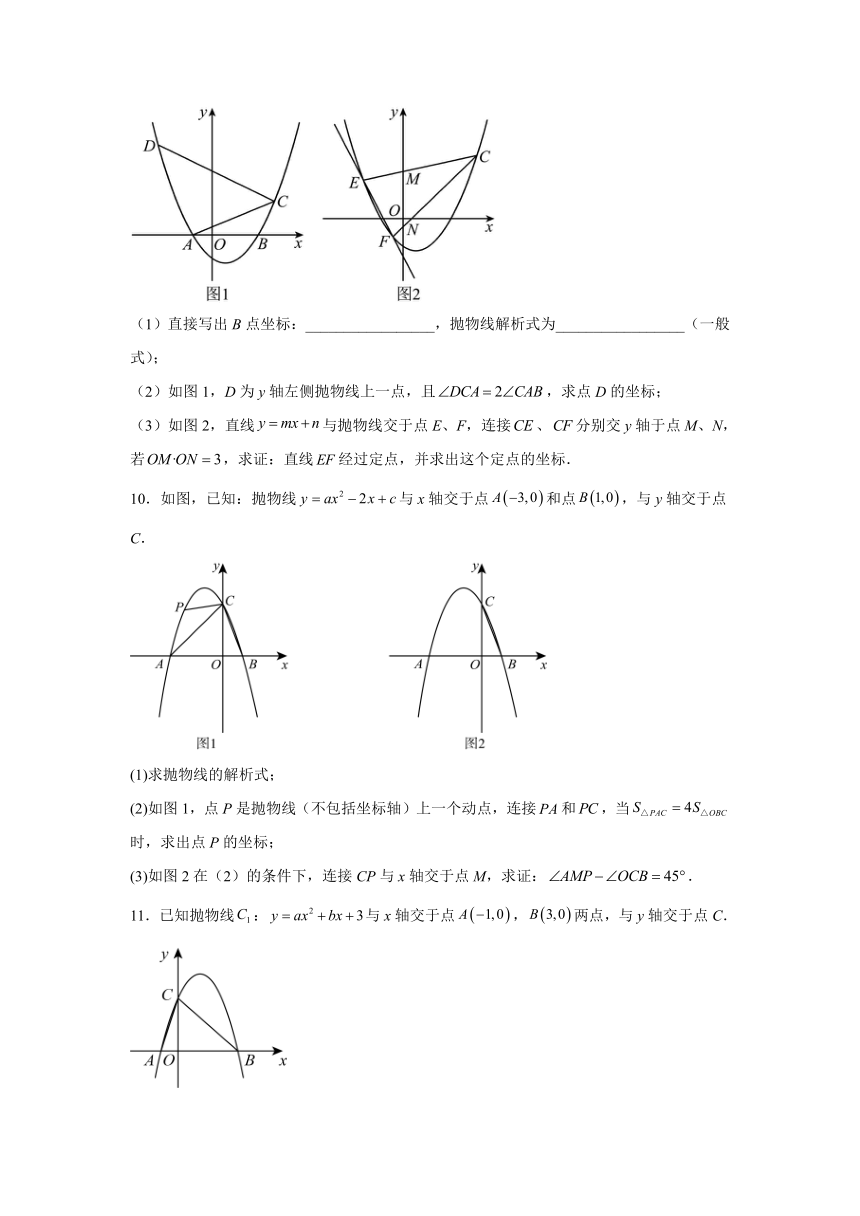
(2)如图1,D为y轴左侧抛物线上一点,且,求点D的坐标;
(3)如图2,直线与抛物线交于点E、F,连接、分别交y轴于点M、N,若,求证:直线经过定点,并求出这个定点的坐标.
10.如图,已知:抛物线与x轴交于点和点,与y轴交于点C.
(1)求抛物线的解析式;
(2)如图1,点P是抛物线(不包括坐标轴)上一个动点,连接和,当时,求出点P的坐标;
(3)如图2在(2)的条件下,连接CP与x轴交于点M,求证:.
11.已知抛物线:与x轴交于点,两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)点M,N是在抛物线的对称轴上两个动点,且,点M在点N的上方,则四边形的周长的最小值为______.
(3)如图,抛物线上是否存在点P,使?若存在,请说明理由;
(4)将抛物线向右平移2个单位长度,再向上平移5个单位长度得到抛物线,若点E为抛物线上的动点,已知点,试证明:以线段为直径的圆截直线所得弦的长为定值,并求出它的值.
12.如图(1),抛物线与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,且,若点D是直线(不与B,C重合)上一动点,过点D作x轴的垂线交抛物线于点E.
(1)求抛物线的解析式.
(2)连接,,当点D的横坐标为时,求证:.
(3)如图(2),若点F是y轴上的动点,是否存在点F,使以点C,D,E,F为顶点的四边形是菱形?若存在,请直接写出点D的坐标;若不存在,请说明理由.
13.抛物线与轴交于、两点,与轴交于点,点在抛物线上.
(1)求抛物线的解析式;
(2)如图1,连接、,点在对称轴左侧的抛物线上,若,求点的坐标;
(3)如图2,点为第四象限抛物线上一点,经过、、三点作,的弦轴,证明:点在直线上.
14.如图,已知直线y=2x+n与抛物线y=ax2+bx+c相交于A,B两点,抛物线的顶点是A(1,﹣4),点B在x轴上.
(1)求抛物线的解析式;
(2)若点M是y轴上一点,点N是坐标平面内一点,当以A、B、M、N为顶点的四边形是矩形时,求点M的坐标.
(3)在抛物线上是否存在点Q,使∠BAQ=45°,若存在,请直接写出点Q的横坐标;若不存在,说明理由.
15.如图,在平面直角坐标系中,二次函数yx2+bx﹣2的图象与x轴交于点A和点B(4,0),与y轴交于点C.
(1)求二次函数的表达式;
(2)若点P是抛物线上一点,满足∠PCB+∠ACB=∠BCO,求点P的坐标;
(3)若点Q在第四象限内,且tan∠AQB,M(﹣2,1),线段MQ是否存在最大值,如果存在,求出最大值;如果不存在,请说明理由.
参考答案:
1.(1)y=﹣x2﹣2x+3,顶点D的坐标为(﹣1,4)
(2)∠ACB
(3)点P坐标为(,)
2.(1),(-1,-4);(2)(-2,-3)或(-4,5)
3.(1),,
(3)点P坐标为或
(4)或
4.抛物线的解析式为,顶点M的坐标为;;P点坐标为或
5.(1);(2)或;(3)C到MN的距离为定值
6.(1)y=x2﹣2x;点M的坐标为(3,﹣3)
(2)点E的坐标为(1,﹣)或(,﹣)
7.(1);(2)4;(4)存在,和.
8.(1),直线的解析式为
(2)①四边形是平行四边形;②或
9.(1),;(2)D坐标为;(3)定点坐标为
10.(1)
(2)
11.(1)
(2)
(3)或
(4)
12.(1)
(3)或或
13.(1).
(2),
14.(1)
(2)点M坐标为:(0,)或(0,)或(0,﹣1)或(0,﹣3)
(3)存在,点Q的横坐标为﹣2或
15.(1)yx2x﹣2
(2)P(,)
(3)
角度问题(二次函数综合)
1.如图,在平面直角坐标系xOy中,抛物线y=ax2-2x+c与x轴交于点A和点B(1,0),与y轴相交于点C(0,3).
(1)求抛物线的解析式和顶点D的坐标;
(2)找出图中与∠DAB相等的一个角,并证明;
(3)若点P是第二象限内抛物线上的一点,当点P到直线AC的距离最大时,求点P的坐标.
2.如图,抛物线y=x2+bx+c与x轴交于点A和点B,交y轴于点C.已知A(﹣3,0),C(0,﹣3),抛物线的顶点为点D.请解答下列问题:
(1)求抛物线的解析式,直接写出顶点D的坐标.
(2)P是抛物线上的一动点,当∠PBO=∠CAO时,则点P的坐标为 .
3.如图,二次函数的图像与轴交于点A,B(点A在点的左侧),与轴交于点,连接,.
(1)直接写出点A,B,C的坐标;
(2)求证:是直角三角形;
(3)点P是该拋物线上一点,若(点为坐标原点),求点的坐标:
(4)点是该抛物线上一点,若(点为坐标原点),直接写出点M的坐标.
4.如图,抛物线过点,交x轴于A,B两点点A在点B的左侧.
求抛物线的解析式,并写出顶点M的坐标;
连接OC,CM,求的值;
若点P在抛物线的对称轴上,连接BP,CP,BM,当时,求点P的坐标.
5.如图1,已知抛物线与x轴交于A,B两点,与y轴交于点D.
(1)求直线BD的解析式;
(2)P为抛物线上一点,当点Р到直线BD的距离为时,求点P的坐标;
(3)如图2,直线交抛物线与M,N两点,C为抛物线上一点,当时,请探究点C到MN的距离是否为定值.
6.如图,在平面直角坐标系中,直线y=﹣x+3与x轴交于点A,与y轴交于点B,抛物线y=x2+bx+c经过坐标原点和点A,顶点为点M.
(1)求抛物线的关系式及点M的坐标;
(2)点E是直线AB下方的抛物线上一动点,连接EB,EA,当△EAB的面积等于时,求E点的坐标;
(3)将直线AB向下平移,得到过点M的直线y=mx+n,且与x轴负半轴交于点C,取点D(2,0),连接DM,求证:∠ADM﹣∠ACM=45°.
7.如图①,二次函数(a≠0)的图象经过点A(,),并且与直线相交于坐标轴上的B、C两点,动点P在直线BC下方的二次函数的图象上.
(1)求此二次函数的表达式;
(2)如图①,连接PC,PB,设△PCB的面积为S,求S的最大值;
(3)如图②,过点A,C作直线,求证AC⊥BC;
(4)如图②,抛物线上是否存在点Q,使得∠ABQ=2∠ABC?若存在,则求出直线BQ的解析式;若不存在,请说明理由.
8.如图1,已知抛物线与x轴交于点和,与y轴交于点C,过点B,C作直线.
(1)求b,c的值和直线的解析式;
(2)点P是直线下方的抛物线上的点,轴与直线交于点D,设点P的横坐标为t.
①如图2,连接,当的面积最大时,试判断四边形的形状,并说明理由;
②如图3,抛物线的对称轴为直线l,直线与x轴交于点E,过点D作直线的垂线,与直线l交于点F,与y轴交于点G,连接.当时,求t的值.
9.如图,抛物线与x轴交于点和B两点,点在抛物线上.
(1)直接写出B点坐标:_________________,抛物线解析式为_________________(一般式);
(2)如图1,D为y轴左侧抛物线上一点,且,求点D的坐标;
(3)如图2,直线与抛物线交于点E、F,连接、分别交y轴于点M、N,若,求证:直线经过定点,并求出这个定点的坐标.
10.如图,已知:抛物线与x轴交于点和点,与y轴交于点C.
(1)求抛物线的解析式;
(2)如图1,点P是抛物线(不包括坐标轴)上一个动点,连接和,当时,求出点P的坐标;
(3)如图2在(2)的条件下,连接CP与x轴交于点M,求证:.
11.已知抛物线:与x轴交于点,两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)点M,N是在抛物线的对称轴上两个动点,且,点M在点N的上方,则四边形的周长的最小值为______.
(3)如图,抛物线上是否存在点P,使?若存在,请说明理由;
(4)将抛物线向右平移2个单位长度,再向上平移5个单位长度得到抛物线,若点E为抛物线上的动点,已知点,试证明:以线段为直径的圆截直线所得弦的长为定值,并求出它的值.
12.如图(1),抛物线与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,且,若点D是直线(不与B,C重合)上一动点,过点D作x轴的垂线交抛物线于点E.
(1)求抛物线的解析式.
(2)连接,,当点D的横坐标为时,求证:.
(3)如图(2),若点F是y轴上的动点,是否存在点F,使以点C,D,E,F为顶点的四边形是菱形?若存在,请直接写出点D的坐标;若不存在,请说明理由.
13.抛物线与轴交于、两点,与轴交于点,点在抛物线上.
(1)求抛物线的解析式;
(2)如图1,连接、,点在对称轴左侧的抛物线上,若,求点的坐标;
(3)如图2,点为第四象限抛物线上一点,经过、、三点作,的弦轴,证明:点在直线上.
14.如图,已知直线y=2x+n与抛物线y=ax2+bx+c相交于A,B两点,抛物线的顶点是A(1,﹣4),点B在x轴上.
(1)求抛物线的解析式;
(2)若点M是y轴上一点,点N是坐标平面内一点,当以A、B、M、N为顶点的四边形是矩形时,求点M的坐标.
(3)在抛物线上是否存在点Q,使∠BAQ=45°,若存在,请直接写出点Q的横坐标;若不存在,说明理由.
15.如图,在平面直角坐标系中,二次函数yx2+bx﹣2的图象与x轴交于点A和点B(4,0),与y轴交于点C.
(1)求二次函数的表达式;
(2)若点P是抛物线上一点,满足∠PCB+∠ACB=∠BCO,求点P的坐标;
(3)若点Q在第四象限内,且tan∠AQB,M(﹣2,1),线段MQ是否存在最大值,如果存在,求出最大值;如果不存在,请说明理由.
参考答案:
1.(1)y=﹣x2﹣2x+3,顶点D的坐标为(﹣1,4)
(2)∠ACB
(3)点P坐标为(,)
2.(1),(-1,-4);(2)(-2,-3)或(-4,5)
3.(1),,
(3)点P坐标为或
(4)或
4.抛物线的解析式为,顶点M的坐标为;;P点坐标为或
5.(1);(2)或;(3)C到MN的距离为定值
6.(1)y=x2﹣2x;点M的坐标为(3,﹣3)
(2)点E的坐标为(1,﹣)或(,﹣)
7.(1);(2)4;(4)存在,和.
8.(1),直线的解析式为
(2)①四边形是平行四边形;②或
9.(1),;(2)D坐标为;(3)定点坐标为
10.(1)
(2)
11.(1)
(2)
(3)或
(4)
12.(1)
(3)或或
13.(1).
(2),
14.(1)
(2)点M坐标为:(0,)或(0,)或(0,﹣1)或(0,﹣3)
(3)存在,点Q的横坐标为﹣2或
15.(1)yx2x﹣2
(2)P(,)
(3)
同课章节目录
