2025年中考数学高频考点突破--特殊三角形问题(二次函数综合)(含简单答案)
文档属性
| 名称 | 2025年中考数学高频考点突破--特殊三角形问题(二次函数综合)(含简单答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 448.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-17 00:00:00 | ||
图片预览




文档简介
2025年中考数学高频考点突破--
特殊三角形问题(二次函数综合)
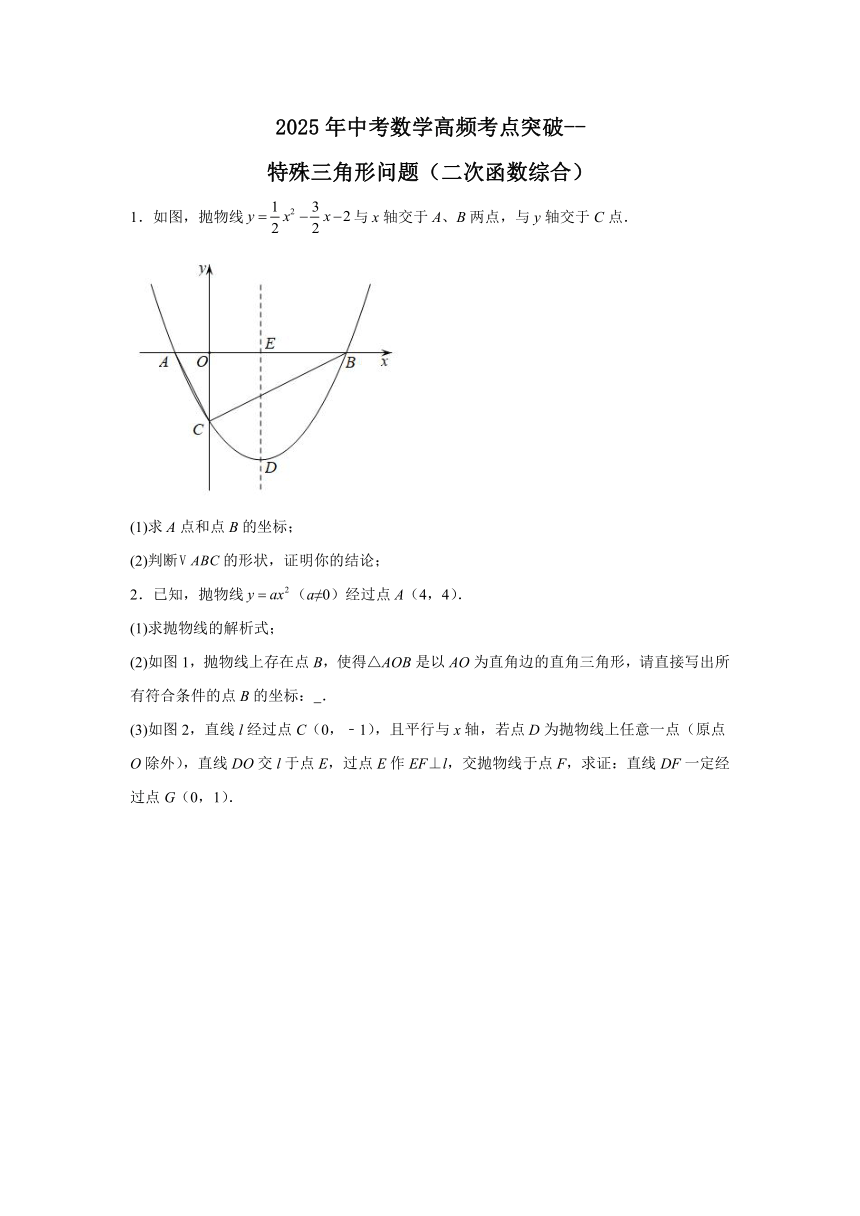
1.如图,抛物线与x轴交于A、B两点,与y轴交于C点.
(1)求A点和点B的坐标;
(2)判断的形状,证明你的结论;
2.已知,抛物线(a≠0)经过点A(4,4).
(1)求抛物线的解析式;
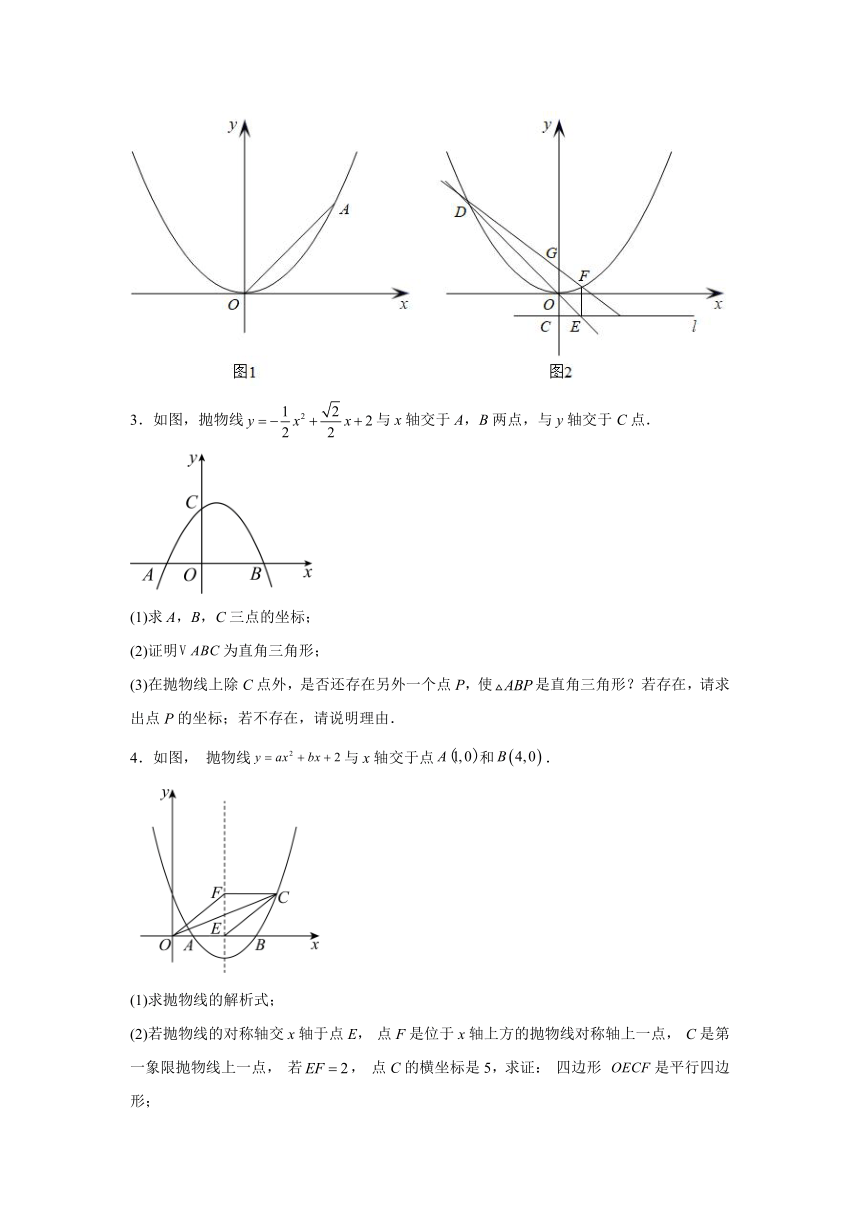
(2)如图1,抛物线上存在点B,使得△AOB是以AO为直角边的直角三角形,请直接写出所有符合条件的点B的坐标: .
(3)如图2,直线l经过点C(0,﹣1),且平行与x轴,若点D为抛物线上任意一点(原点O除外),直线DO交l于点E,过点E作EF⊥l,交抛物线于点F,求证:直线DF一定经过点G(0,1).
3.如图,抛物线与x轴交于A,B两点,与y轴交于C点.
(1)求A,B,C三点的坐标;
(2)证明为直角三角形;
(3)在抛物线上除C点外,是否还存在另外一个点P,使是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
4.如图, 抛物线与x轴交于点和.
(1)求抛物线的解析式;
(2)若抛物线的对称轴交x轴于点E, 点F是位于x轴上方的抛物线对称轴上一点, C是第一象限抛物线上一点, 若, 点C的横坐标是5,求证: 四边形 是平行四边形;
(3)在(2)的条件下,若点P是x轴上的一个动点,当是等腰三角形时,求点 P的坐标.
5.如图1,抛物线与轴交于点、,与轴交于点,点是抛物线上的动点,连接、,与轴交于点.
(1)求该抛物线所对应的函数解析式;
(2)若点的坐标为,请求出此时的面积;
(3)过点作轴的平行线交轴于点,交直线于点,如图2.
①若,求证:;
②能否为等腰三角形?若能,请求出此时点的坐标;若不能,请说明理由.
6.二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(-3,0)、B(1,0)两点,与y轴交于点C(0,-3m)(其中m>0),顶点为D.
(1)用含m的代数式分别表示a、b、c;
(2)如图,当m取何值时,△ADC为直角三角形?
7.如图,在平面直角坐标系中,点A的坐标为(-1,-1),点B的坐标为(3,-3),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.
(1)求抛物线及线段OB所在直线的解析式;
(2)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.
①求△BOD 面积的最大值,并求出此时点D的坐标;
②当△OPC为等腰三角形时,直接写出点P的坐标.
8.如图,在平面直角坐标系中,—抛物线y=﹣a(x+1)(x﹣3)(a>0)与x轴交于A、B两点,与y轴交于点C.抛物线的对称轴与x轴交于点E,过点C作x轴的平行线,与抛物线交于点D,连接DE,延长DE交y轴于点F,连接AD、AF.
(1)点A的坐标为____________,点B的坐标为_________ ;
(2)判断四边形ACDE的形状,并给出证明;
(3)当a为何值时,△ADF是直角三角形
9.如图,二次函数图象的顶点坐标为,且在轴上截得的线段的长为2.
(1)求证:是等腰直角三角形;
(2)求二次函数的解析式;
(3)在的抛物线上是否存在点,使是等腰三角形;若存在,请直接写出点的坐标,若不存在,请说明理由.
10.如图,二次函数的图象与轴交于和两点,与轴交于点,点是直线下方的抛物线上一动点,过点作轴于点,交直线于点.
(1)求点和点的坐标;
(2)求线段的最大值及此时点的坐标;
(3)当最大时,在二次函数的图象上是否存在点,使以点为顶点的三角形是直角三角形?若存在,求点的坐标,若不存在,请说明理由.
11.已知抛物线y=ax2+bx+c(b<0)与x轴只有一个公共点.
(1)若公共点坐标为(2,0),求a、c满足的关系式;
(2)设A为抛物线上的一定点,直线l:y=kx+1-k与抛物线交于点B、C两点,直线BD垂直于直线y=-1,垂足为点D.当k=0时,直线l与抛物线的一个交点在 y轴上,且△ABC为等腰直角三角形.
①求点A的坐标和抛物线的解析式;
②证明:对于每个给定的实数 k,都有A、D、C三点共线.
12.如图,抛物线y=+bx+c的对称轴为x=﹣1,该抛物线与x轴交于A、B两点,且A点坐标为(1,0),交y轴于C(0,3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标.
(2)试判断△BCD的形状,并予证明.
(3)在对称轴上是否存在一点P,使得△ACP为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
13.如图,顶点为()的二次函数图象与轴交于点,点在该图象上,直线交二次函数图象对称轴于点,点、关于点对称,连接、.
(1)求该二次函数的关系式(用含的式子表示).
(2)若点在对称轴右侧的二次函数图象上运动,请解答下列问题:
①连接,当时,请判断的形状,并说明理由.
②求证:.
14.已知抛物线经过、两点,O为坐标原点,抛物线交正方形的边于点E,点M为射线上一动点,连接,交于点F.
(1)求b和c的值及点C的坐标;
(2)求证∶
(3)是否存在点M,使为等腰三角形?若不存在,请说明理由;若存在,求ME的长.
15.如图,二次函数(其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD,过点A作射线AE交二次函数的图象于点E,AB平分∠DAE
(1)用含m的代数式表示a;
(2))求证:为定值;
(3)设该二次函数图象的顶点为F.探索:在x轴的负半轴上是否存在点G,连接CF,以线段GF、AD、AE的长度为三边长的三角形是直角三角形?如果存在,只要找出一个满足要求的点G即可,并用含m的代数式表示该点的横坐标;如果不存在,请说明理由.
参考答案:
1.(1);
(2)是直角三角形
2.(1),
(2)B(﹣4,4)或(﹣8,16);
3.(1)
(3)存在,
4.(1)抛物线的解析式为
(3)点P坐标为或或或
5.(1)
(2)15
(3)②能,,,,,,.
6.(1)a=m,b=2m,c=-3m;(2)m=1或m=.
7.(1)抛物线的解析式为.直线OB的解析式为y=-x.(2)
8.(1)点A(﹣1,0),点B(3,0);(2)四边形ACDE是平行四边形(3)当或时,△ADF为直角三角形.
9.(2)
(3)在的抛物线上存在点,使是等腰三角形,点或或
10.(1)
(2)当时,线段的最大值为4,此时点的坐标为
(3)存在,或或
11.(1) y=a(x-2)2, c=4a;(2) ①顶点A(1,0),y= x2-2x+1
12.(1)y=﹣2x+3,顶点D为(﹣1,4);(2)△DCB为直角三角形;(3) 存在满足条件的点P,其坐标为(﹣1,1)或(﹣1,)或(﹣1,)或(﹣1,0)或(﹣1,6).
13.(1);(2)①等腰直角三角形
14.(1),,
(3)存在,或
15.(1);(3)以线段GF、AD、AE的长度为三边长的三角形是直角三角形,此时点G的横坐标为-3m.
特殊三角形问题(二次函数综合)
1.如图,抛物线与x轴交于A、B两点,与y轴交于C点.
(1)求A点和点B的坐标;
(2)判断的形状,证明你的结论;
2.已知,抛物线(a≠0)经过点A(4,4).
(1)求抛物线的解析式;
(2)如图1,抛物线上存在点B,使得△AOB是以AO为直角边的直角三角形,请直接写出所有符合条件的点B的坐标: .
(3)如图2,直线l经过点C(0,﹣1),且平行与x轴,若点D为抛物线上任意一点(原点O除外),直线DO交l于点E,过点E作EF⊥l,交抛物线于点F,求证:直线DF一定经过点G(0,1).
3.如图,抛物线与x轴交于A,B两点,与y轴交于C点.
(1)求A,B,C三点的坐标;
(2)证明为直角三角形;
(3)在抛物线上除C点外,是否还存在另外一个点P,使是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
4.如图, 抛物线与x轴交于点和.
(1)求抛物线的解析式;
(2)若抛物线的对称轴交x轴于点E, 点F是位于x轴上方的抛物线对称轴上一点, C是第一象限抛物线上一点, 若, 点C的横坐标是5,求证: 四边形 是平行四边形;
(3)在(2)的条件下,若点P是x轴上的一个动点,当是等腰三角形时,求点 P的坐标.
5.如图1,抛物线与轴交于点、,与轴交于点,点是抛物线上的动点,连接、,与轴交于点.
(1)求该抛物线所对应的函数解析式;
(2)若点的坐标为,请求出此时的面积;
(3)过点作轴的平行线交轴于点,交直线于点,如图2.
①若,求证:;
②能否为等腰三角形?若能,请求出此时点的坐标;若不能,请说明理由.
6.二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(-3,0)、B(1,0)两点,与y轴交于点C(0,-3m)(其中m>0),顶点为D.
(1)用含m的代数式分别表示a、b、c;
(2)如图,当m取何值时,△ADC为直角三角形?
7.如图,在平面直角坐标系中,点A的坐标为(-1,-1),点B的坐标为(3,-3),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.
(1)求抛物线及线段OB所在直线的解析式;
(2)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.
①求△BOD 面积的最大值,并求出此时点D的坐标;
②当△OPC为等腰三角形时,直接写出点P的坐标.
8.如图,在平面直角坐标系中,—抛物线y=﹣a(x+1)(x﹣3)(a>0)与x轴交于A、B两点,与y轴交于点C.抛物线的对称轴与x轴交于点E,过点C作x轴的平行线,与抛物线交于点D,连接DE,延长DE交y轴于点F,连接AD、AF.
(1)点A的坐标为____________,点B的坐标为_________ ;
(2)判断四边形ACDE的形状,并给出证明;
(3)当a为何值时,△ADF是直角三角形
9.如图,二次函数图象的顶点坐标为,且在轴上截得的线段的长为2.
(1)求证:是等腰直角三角形;
(2)求二次函数的解析式;
(3)在的抛物线上是否存在点,使是等腰三角形;若存在,请直接写出点的坐标,若不存在,请说明理由.
10.如图,二次函数的图象与轴交于和两点,与轴交于点,点是直线下方的抛物线上一动点,过点作轴于点,交直线于点.
(1)求点和点的坐标;
(2)求线段的最大值及此时点的坐标;
(3)当最大时,在二次函数的图象上是否存在点,使以点为顶点的三角形是直角三角形?若存在,求点的坐标,若不存在,请说明理由.
11.已知抛物线y=ax2+bx+c(b<0)与x轴只有一个公共点.
(1)若公共点坐标为(2,0),求a、c满足的关系式;
(2)设A为抛物线上的一定点,直线l:y=kx+1-k与抛物线交于点B、C两点,直线BD垂直于直线y=-1,垂足为点D.当k=0时,直线l与抛物线的一个交点在 y轴上,且△ABC为等腰直角三角形.
①求点A的坐标和抛物线的解析式;
②证明:对于每个给定的实数 k,都有A、D、C三点共线.
12.如图,抛物线y=+bx+c的对称轴为x=﹣1,该抛物线与x轴交于A、B两点,且A点坐标为(1,0),交y轴于C(0,3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标.
(2)试判断△BCD的形状,并予证明.
(3)在对称轴上是否存在一点P,使得△ACP为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
13.如图,顶点为()的二次函数图象与轴交于点,点在该图象上,直线交二次函数图象对称轴于点,点、关于点对称,连接、.
(1)求该二次函数的关系式(用含的式子表示).
(2)若点在对称轴右侧的二次函数图象上运动,请解答下列问题:
①连接,当时,请判断的形状,并说明理由.
②求证:.
14.已知抛物线经过、两点,O为坐标原点,抛物线交正方形的边于点E,点M为射线上一动点,连接,交于点F.
(1)求b和c的值及点C的坐标;
(2)求证∶
(3)是否存在点M,使为等腰三角形?若不存在,请说明理由;若存在,求ME的长.
15.如图,二次函数(其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD,过点A作射线AE交二次函数的图象于点E,AB平分∠DAE
(1)用含m的代数式表示a;
(2))求证:为定值;
(3)设该二次函数图象的顶点为F.探索:在x轴的负半轴上是否存在点G,连接CF,以线段GF、AD、AE的长度为三边长的三角形是直角三角形?如果存在,只要找出一个满足要求的点G即可,并用含m的代数式表示该点的横坐标;如果不存在,请说明理由.
参考答案:
1.(1);
(2)是直角三角形
2.(1),
(2)B(﹣4,4)或(﹣8,16);
3.(1)
(3)存在,
4.(1)抛物线的解析式为
(3)点P坐标为或或或
5.(1)
(2)15
(3)②能,,,,,,.
6.(1)a=m,b=2m,c=-3m;(2)m=1或m=.
7.(1)抛物线的解析式为.直线OB的解析式为y=-x.(2)
8.(1)点A(﹣1,0),点B(3,0);(2)四边形ACDE是平行四边形(3)当或时,△ADF为直角三角形.
9.(2)
(3)在的抛物线上存在点,使是等腰三角形,点或或
10.(1)
(2)当时,线段的最大值为4,此时点的坐标为
(3)存在,或或
11.(1) y=a(x-2)2, c=4a;(2) ①顶点A(1,0),y= x2-2x+1
12.(1)y=﹣2x+3,顶点D为(﹣1,4);(2)△DCB为直角三角形;(3) 存在满足条件的点P,其坐标为(﹣1,1)或(﹣1,)或(﹣1,)或(﹣1,0)或(﹣1,6).
13.(1);(2)①等腰直角三角形
14.(1),,
(3)存在,或
15.(1);(3)以线段GF、AD、AE的长度为三边长的三角形是直角三角形,此时点G的横坐标为-3m.
同课章节目录
