6.1分类加法计数原理与分步乘法计数原理 同步练习(含解析) 高二数学人教A版(2019)选择性必修三
文档属性
| 名称 | 6.1分类加法计数原理与分步乘法计数原理 同步练习(含解析) 高二数学人教A版(2019)选择性必修三 |
|
|
| 格式 | docx | ||
| 文件大小 | 143.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-15 13:41:37 | ||
图片预览




文档简介
6.1 分类加法计数原理与分步乘法计数原理
教材课后习题
1.一个商店销售某种型号的电视机,其中本地的产品有4种,外地的产品有7种.要买1台这种型号的电视机,有多少种不同的选法?
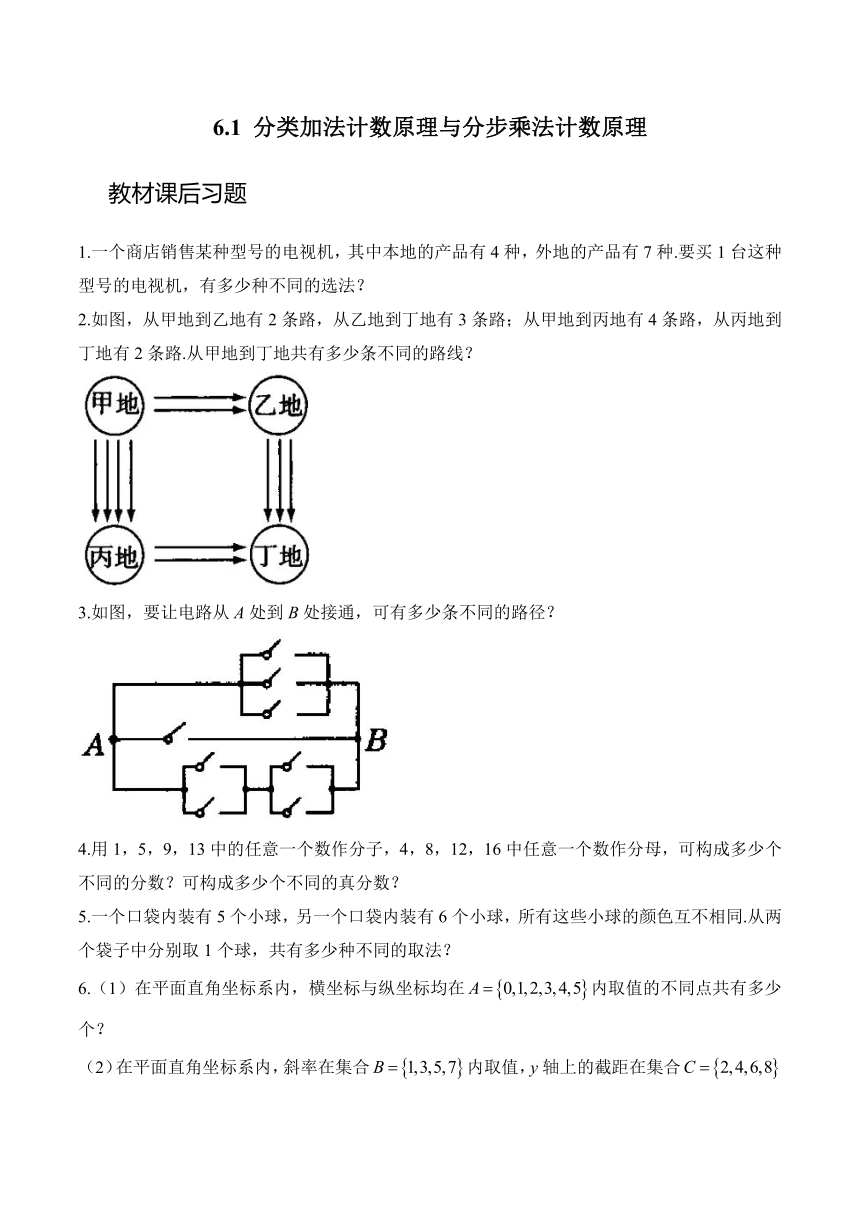
2.如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4条路,从丙地到丁地有2条路.从甲地到丁地共有多少条不同的路线?
3.如图,要让电路从A处到B处接通,可有多少条不同的路径?
4.用1,5,9,13中的任意一个数作分子,4,8,12,16中任意一个数作分母,可构成多少个不同的分数?可构成多少个不同的真分数?
5.一个口袋内装有5个小球,另一个口袋内装有6个小球,所有这些小球的颜色互不相同.从两个袋子中分别取1个球,共有多少种不同的取法?
6.(1)在平面直角坐标系内,横坐标与纵坐标均在内取值的不同点共有多少个?
(2)在平面直角坐标系内,斜率在集合内取值,y轴上的截距在集合内取值的不同直线共有多少条?
7.一种号码锁有4个拨号盘,每个拨号盘上有0~9共10个数字.现最后一个拨号盘出现了故障,只能在0~5这6个数字中拨号,这4个拨号盘可组成多少个四位数字号码?
8.(1)4名同学分别报名参加学校的足球队、篮球队、乒乓球队,每人限报其中的一个运动队,不同报法的种数是还是?
(2)3个班分别从5个景点中选择一处游览,不同选法的种数是还是?
9.(1)从5件不同的礼物中选出4件送给4位同学,每人一件,有多少种不同的送法?
(2)有5个编了号的抽屉,要放进3本不同的书,不同的放法有多少种?(一个抽屉可放多本书)
10.口袋中装有8个白球和10个红球,每个球编有不同的号码,现从中取出2个球.
(1)正好是白球、红球各一个的取法有多少种?
(2)正好是两个白球的取法有多少种?
(3)至少有一个白球的取法有多少种?
(4)两球的颜色相同的取法有多少种?
11.在国庆长假期间,要从7人中选若干人在7天假期值班(每天只需1人值班),不出现同一人连续值班2天,有多少种可能的安排方法?
12.2160有多少个不同的正因数?
定点变式训练
13.甲、乙、丙三人踢毽子,互相传递,每人每次只能踢一下,由甲开始踢,经过4次传递后,毽子又被踢回给甲,则不同的传递方式共有( )
A.4种 B.6种 C.10种 D.16种
14.2022年北京冬奥会的顺利召开引起了大家对冰雪运动的关注.若A,B,C三人在自由式滑雪、花样滑冰、冰壶和跳台滑雪这四项运动中任选一项进行体验,则不同的选法共有( )
A.12种 B.16种 C.64种 D.81种
15.中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)中的一种.现有十二生肖的吉祥物各一个,已知甲同学喜欢牛、马和猴,乙同学喜欢牛、狗和羊,丙同学所有的吉祥物都喜欢.现让甲、乙、丙三位同学依次从中选一个作为礼物珍藏,若各人所选取的礼物都是自己喜欢的,则不同的选法共有( )
A.50种 B.60种 C.80种 D.90种
16.春节期间,某地政府在该地的一个广场布置了一个如图的圆形花坛,花坛分为5个区域.现有5种不同的花卉可供选择,要求相邻区域不能布置相同的花卉,且每个区域只布置一种花卉,则不同的布置方案有( )
A.120种 B.240种 C.420种 D.720种
17.已知某超市为顾客提供四种结账方式:现金、支付平台A、支付平台B、银联卡.顾客甲只会用现金结账,顾客乙只会用现金和银联卡结账,顾客丙与甲、乙结账方式不同,顾客丁用哪种结账方式都可以.若甲、乙、丙、丁购物后依次结账,则他们结账方式的组合种数为__________.
18.现有3名高一学生和5名高二学生,从中选择一人作为国旗下讲话的主持人,则不同的选法种数是__________;若要从高一年级的3名学生和高二年级的5名学生中各选择一人作为国旗下讲话的主持人,则不同的选法种数是__________.
19.设有3名医生、5名护士、2名麻醉师.
(1)从中选派1人外出参加学习,有多少种不同的选法?
(2)从这些人中选出1名医生、1名护士和1名麻醉师组成1个医疗小组,有多少种不同的选法?
答案以及解析
1.答案:11种
解析:一件事情是“买1台某种型号的电视机”,
因此选法有种.
2.答案:14条
解析:一件事情是“从甲地经乙地或经丙地到丁地”,所以是“先分类,后分步”.
不同的路线共有条.
3.答案:8条
解析:一件事情是“接通电路”.根据电路的有关知识,容易得到不同的接通路径有条.
4.答案:可构成的分数的个数为16,可构成的真分数的个数为10
解析:对于第一问,一件事情是“构成一个分数”.
由于1,5,9,13是奇数,4,8,12,16是偶数,
所以以1,5,9,13中任意一个数为分子,以4,8,12,16中的任意一个数为分母可以构成不重复的分数,
因此可以分两步来构成分数:
第一步,选分子,有4种选法;第二步,选分母,也有4种进法.
故可构成的分数的个数为.
对于第二问,一件事情是“构成一个真分数”.分四类:
分子为1时,分母可以从4,8,12,16中任选一个数,有4个;
分子为5时,分母可以从8,12,16中任选一个数,有3个;
分子为9时,分母可以从12,16中任选一个数,有2个;
分子为13时,分母只能选16,有1个.
所以可构成的真分数的个数为.
5.答案:30
解析:一件事情是“从两个袋子中分别取1个球”,
由分步乘法计数原理,不同的取法数为.
6.答案:(1)36个
(2)16条
解析:(1)一件事情是“用坐标确定点”.由于横、纵坐标可以相同,因此可以分两步完成:
第一步,从A中选横坐标,有6种选择;第二步,从A中选取纵坐标,也有6种选择.
所以共有个不同的点.
(2)一件事情是“确定一条直线”.由于斜率不同截距不同、斜率不同截距相同、斜率相同截距不同的直线都是互不相同的,
因此可分两步完成:第一步,取斜率,有4种取法;第二步,取截距,有4种取法.
所以共有不同的直线条.
7.答案:6000
解析:一件事情是“组成一个四位数字号码”.由于数字可以重复,最后一个数字只能在0~5这6个数字中选择,
所以可组成的四位数字号码的个数为.
8.答案:(1)
(2)
解析:(1)一件事情是“4名同学分别参加3个运动队中的一个,每人限报一个,可以报同一个运动队”,应该是人选运动队,
所以不同报法种数是.
(2)一件事情是“3个班分别从5个景点中选择一处游览”,应该是班选景点,
故不同的选法种数是.
9.答案:(1)120种
(2)125种
解析:(1)一件事情是“从5件不同礼物中选4件送给4位同学,每人1件”,应该分4步,每步选一件礼物送给一个同学,
由分步乘法计数原理共有种.
(2)一件事情是“把3本不同的书放进抽屉,每本书都可放进5个不同的抽屉中的任意一个”,是书选抽屉,
所以不同的放法有种.
10.答案:(1)80种
(2)28种
(3)108种
(4)73种
解析:(1)一件事情是“取出一个白球一个红球”.可分2步解决,第1步取一个白球,8种取法;第2步取一个红球,10种取法,
由分步乘法计数原理,共有种不同取法.
(2)一件事情是“取出两个白球”.可分为2步解决,先从8个白球中取一个,8种取法;
再从余下7个白球中取一个,7种取法,
但先取1号球后取2号球与先取2号球后取1号球,结果是相同的,
故共有种不同的取法.
(3)一件事情是“取出一个白球一个红球或者取出两个白球”,可分两类解决,
取出一个白球一个红球有80种不同取法;
取出两个白球有28种不同取法,
由分类加法计数原理,共有种不同取法.
(4)一件事情是“取出两白球或取出两红球”.可分两类解决,取出两白球有28种不同取法:取出两红球有种不同取法,
由分类加法计数原理知,共有种不同取法.
11.答案:326592种
解析:利用分步乘法计数原理,分七步来求解.
第一步,安排第一天的值班人员,有7种方法;
第二步,安排第二天的值班人员,有6种方法;
第三步,安排第三天的值班人员,有6种方法;
同理,第四、五、六、七步均有6种方法.
综上所述,共有种可能的安排方法.
12.答案:40个
解析:,
若没2160的正因数,
则,,,
的正因数共有个.
13.答案:B
解析:分2类:甲第一次踢给乙时,满足条件的有3种方法(如图).同理,甲先踢给丙时,满足条件的也有3种方法.由分类加法计数原理可知,共有(种)传递方式.故选B.
14.答案:C
解析:每个人都可在四项运动中选一项,即每人都有四种选法,可分三步完成,则根据分步乘法计数原理,得不同的选法共有(种).故选C.
15.答案:C
解析:按甲的不同选择分成两种情况讨论:若甲选择牛,此时乙的选择有2种,丙的选择有10种,共有(种)不同的选法;
若甲选择马或猴,此时甲的选择有2种,乙的选择有3种,丙的选择有10种,共有(种)不同的选法.
综上可知,一共有(种)不同的选法.故选C.
16.答案:C
解析:如图,先在区域A中种植,有5种不同的选择,再在区域B中种植,有4种不同的选择,再在区域C中种植,有3种不同的选择.在区域D中种植,若区域D与区域B种植同一种花卉,则区域E有3种不同的选择;若区域D与区域B种植不同的花卉,则区域D有2种不同的选择,区域E有2种不同的选择.所以不同的布置方案有(种).故选C.
17.答案:20
解析:当乙用现金结账时,甲和乙都用现金结账,所以丙有3种结账方式,丁有4种结账方式,故共有(种)结账方式;当乙用银联卡结账时,甲用现金结账,所以丙有2种结账方式,丁有4种结账方式,故共有(种)结账方式.综上可知,共有(种)结账方式.
18.答案:8;15
解析:根据题意,从中选择一人作为国旗下讲话的主持人,若从高一学生中选,则有3种选法;若从高二学生中选,则有5种选法.由分类加法计数原理知,共有(种)不同的选法.若要从高一年级的3名学生和高二年级的5名学生中各选择一人作为国旗下讲话的主持人,从高一学生中选出一人,有3种选法,从高二学生中选出一人,有5种选法,则有(种)不同的选法.
19.答案:(1)10种
(2)30种
解析:(1)分3类;
第1类:从医生中选,有3种选法.
第2类:从护士中选,有5种选法.
第3类:从麻醉师中选,有2种选法.
根据分类加法计数原理,可知共有(种)不同的选法.
(2)分3步:
第1步:选1名医生,有3种选法.
第2步:选1名护士,有5种选法.
第3步:选1名麻醉师,有2种选法.
根据分步乘法计数原理,可知共有(种)不同的选法.
教材课后习题
1.一个商店销售某种型号的电视机,其中本地的产品有4种,外地的产品有7种.要买1台这种型号的电视机,有多少种不同的选法?
2.如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4条路,从丙地到丁地有2条路.从甲地到丁地共有多少条不同的路线?
3.如图,要让电路从A处到B处接通,可有多少条不同的路径?
4.用1,5,9,13中的任意一个数作分子,4,8,12,16中任意一个数作分母,可构成多少个不同的分数?可构成多少个不同的真分数?
5.一个口袋内装有5个小球,另一个口袋内装有6个小球,所有这些小球的颜色互不相同.从两个袋子中分别取1个球,共有多少种不同的取法?
6.(1)在平面直角坐标系内,横坐标与纵坐标均在内取值的不同点共有多少个?
(2)在平面直角坐标系内,斜率在集合内取值,y轴上的截距在集合内取值的不同直线共有多少条?
7.一种号码锁有4个拨号盘,每个拨号盘上有0~9共10个数字.现最后一个拨号盘出现了故障,只能在0~5这6个数字中拨号,这4个拨号盘可组成多少个四位数字号码?
8.(1)4名同学分别报名参加学校的足球队、篮球队、乒乓球队,每人限报其中的一个运动队,不同报法的种数是还是?
(2)3个班分别从5个景点中选择一处游览,不同选法的种数是还是?
9.(1)从5件不同的礼物中选出4件送给4位同学,每人一件,有多少种不同的送法?
(2)有5个编了号的抽屉,要放进3本不同的书,不同的放法有多少种?(一个抽屉可放多本书)
10.口袋中装有8个白球和10个红球,每个球编有不同的号码,现从中取出2个球.
(1)正好是白球、红球各一个的取法有多少种?
(2)正好是两个白球的取法有多少种?
(3)至少有一个白球的取法有多少种?
(4)两球的颜色相同的取法有多少种?
11.在国庆长假期间,要从7人中选若干人在7天假期值班(每天只需1人值班),不出现同一人连续值班2天,有多少种可能的安排方法?
12.2160有多少个不同的正因数?
定点变式训练
13.甲、乙、丙三人踢毽子,互相传递,每人每次只能踢一下,由甲开始踢,经过4次传递后,毽子又被踢回给甲,则不同的传递方式共有( )
A.4种 B.6种 C.10种 D.16种
14.2022年北京冬奥会的顺利召开引起了大家对冰雪运动的关注.若A,B,C三人在自由式滑雪、花样滑冰、冰壶和跳台滑雪这四项运动中任选一项进行体验,则不同的选法共有( )
A.12种 B.16种 C.64种 D.81种
15.中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)中的一种.现有十二生肖的吉祥物各一个,已知甲同学喜欢牛、马和猴,乙同学喜欢牛、狗和羊,丙同学所有的吉祥物都喜欢.现让甲、乙、丙三位同学依次从中选一个作为礼物珍藏,若各人所选取的礼物都是自己喜欢的,则不同的选法共有( )
A.50种 B.60种 C.80种 D.90种
16.春节期间,某地政府在该地的一个广场布置了一个如图的圆形花坛,花坛分为5个区域.现有5种不同的花卉可供选择,要求相邻区域不能布置相同的花卉,且每个区域只布置一种花卉,则不同的布置方案有( )
A.120种 B.240种 C.420种 D.720种
17.已知某超市为顾客提供四种结账方式:现金、支付平台A、支付平台B、银联卡.顾客甲只会用现金结账,顾客乙只会用现金和银联卡结账,顾客丙与甲、乙结账方式不同,顾客丁用哪种结账方式都可以.若甲、乙、丙、丁购物后依次结账,则他们结账方式的组合种数为__________.
18.现有3名高一学生和5名高二学生,从中选择一人作为国旗下讲话的主持人,则不同的选法种数是__________;若要从高一年级的3名学生和高二年级的5名学生中各选择一人作为国旗下讲话的主持人,则不同的选法种数是__________.
19.设有3名医生、5名护士、2名麻醉师.
(1)从中选派1人外出参加学习,有多少种不同的选法?
(2)从这些人中选出1名医生、1名护士和1名麻醉师组成1个医疗小组,有多少种不同的选法?
答案以及解析
1.答案:11种
解析:一件事情是“买1台某种型号的电视机”,
因此选法有种.
2.答案:14条
解析:一件事情是“从甲地经乙地或经丙地到丁地”,所以是“先分类,后分步”.
不同的路线共有条.
3.答案:8条
解析:一件事情是“接通电路”.根据电路的有关知识,容易得到不同的接通路径有条.
4.答案:可构成的分数的个数为16,可构成的真分数的个数为10
解析:对于第一问,一件事情是“构成一个分数”.
由于1,5,9,13是奇数,4,8,12,16是偶数,
所以以1,5,9,13中任意一个数为分子,以4,8,12,16中的任意一个数为分母可以构成不重复的分数,
因此可以分两步来构成分数:
第一步,选分子,有4种选法;第二步,选分母,也有4种进法.
故可构成的分数的个数为.
对于第二问,一件事情是“构成一个真分数”.分四类:
分子为1时,分母可以从4,8,12,16中任选一个数,有4个;
分子为5时,分母可以从8,12,16中任选一个数,有3个;
分子为9时,分母可以从12,16中任选一个数,有2个;
分子为13时,分母只能选16,有1个.
所以可构成的真分数的个数为.
5.答案:30
解析:一件事情是“从两个袋子中分别取1个球”,
由分步乘法计数原理,不同的取法数为.
6.答案:(1)36个
(2)16条
解析:(1)一件事情是“用坐标确定点”.由于横、纵坐标可以相同,因此可以分两步完成:
第一步,从A中选横坐标,有6种选择;第二步,从A中选取纵坐标,也有6种选择.
所以共有个不同的点.
(2)一件事情是“确定一条直线”.由于斜率不同截距不同、斜率不同截距相同、斜率相同截距不同的直线都是互不相同的,
因此可分两步完成:第一步,取斜率,有4种取法;第二步,取截距,有4种取法.
所以共有不同的直线条.
7.答案:6000
解析:一件事情是“组成一个四位数字号码”.由于数字可以重复,最后一个数字只能在0~5这6个数字中选择,
所以可组成的四位数字号码的个数为.
8.答案:(1)
(2)
解析:(1)一件事情是“4名同学分别参加3个运动队中的一个,每人限报一个,可以报同一个运动队”,应该是人选运动队,
所以不同报法种数是.
(2)一件事情是“3个班分别从5个景点中选择一处游览”,应该是班选景点,
故不同的选法种数是.
9.答案:(1)120种
(2)125种
解析:(1)一件事情是“从5件不同礼物中选4件送给4位同学,每人1件”,应该分4步,每步选一件礼物送给一个同学,
由分步乘法计数原理共有种.
(2)一件事情是“把3本不同的书放进抽屉,每本书都可放进5个不同的抽屉中的任意一个”,是书选抽屉,
所以不同的放法有种.
10.答案:(1)80种
(2)28种
(3)108种
(4)73种
解析:(1)一件事情是“取出一个白球一个红球”.可分2步解决,第1步取一个白球,8种取法;第2步取一个红球,10种取法,
由分步乘法计数原理,共有种不同取法.
(2)一件事情是“取出两个白球”.可分为2步解决,先从8个白球中取一个,8种取法;
再从余下7个白球中取一个,7种取法,
但先取1号球后取2号球与先取2号球后取1号球,结果是相同的,
故共有种不同的取法.
(3)一件事情是“取出一个白球一个红球或者取出两个白球”,可分两类解决,
取出一个白球一个红球有80种不同取法;
取出两个白球有28种不同取法,
由分类加法计数原理,共有种不同取法.
(4)一件事情是“取出两白球或取出两红球”.可分两类解决,取出两白球有28种不同取法:取出两红球有种不同取法,
由分类加法计数原理知,共有种不同取法.
11.答案:326592种
解析:利用分步乘法计数原理,分七步来求解.
第一步,安排第一天的值班人员,有7种方法;
第二步,安排第二天的值班人员,有6种方法;
第三步,安排第三天的值班人员,有6种方法;
同理,第四、五、六、七步均有6种方法.
综上所述,共有种可能的安排方法.
12.答案:40个
解析:,
若没2160的正因数,
则,,,
的正因数共有个.
13.答案:B
解析:分2类:甲第一次踢给乙时,满足条件的有3种方法(如图).同理,甲先踢给丙时,满足条件的也有3种方法.由分类加法计数原理可知,共有(种)传递方式.故选B.
14.答案:C
解析:每个人都可在四项运动中选一项,即每人都有四种选法,可分三步完成,则根据分步乘法计数原理,得不同的选法共有(种).故选C.
15.答案:C
解析:按甲的不同选择分成两种情况讨论:若甲选择牛,此时乙的选择有2种,丙的选择有10种,共有(种)不同的选法;
若甲选择马或猴,此时甲的选择有2种,乙的选择有3种,丙的选择有10种,共有(种)不同的选法.
综上可知,一共有(种)不同的选法.故选C.
16.答案:C
解析:如图,先在区域A中种植,有5种不同的选择,再在区域B中种植,有4种不同的选择,再在区域C中种植,有3种不同的选择.在区域D中种植,若区域D与区域B种植同一种花卉,则区域E有3种不同的选择;若区域D与区域B种植不同的花卉,则区域D有2种不同的选择,区域E有2种不同的选择.所以不同的布置方案有(种).故选C.
17.答案:20
解析:当乙用现金结账时,甲和乙都用现金结账,所以丙有3种结账方式,丁有4种结账方式,故共有(种)结账方式;当乙用银联卡结账时,甲用现金结账,所以丙有2种结账方式,丁有4种结账方式,故共有(种)结账方式.综上可知,共有(种)结账方式.
18.答案:8;15
解析:根据题意,从中选择一人作为国旗下讲话的主持人,若从高一学生中选,则有3种选法;若从高二学生中选,则有5种选法.由分类加法计数原理知,共有(种)不同的选法.若要从高一年级的3名学生和高二年级的5名学生中各选择一人作为国旗下讲话的主持人,从高一学生中选出一人,有3种选法,从高二学生中选出一人,有5种选法,则有(种)不同的选法.
19.答案:(1)10种
(2)30种
解析:(1)分3类;
第1类:从医生中选,有3种选法.
第2类:从护士中选,有5种选法.
第3类:从麻醉师中选,有2种选法.
根据分类加法计数原理,可知共有(种)不同的选法.
(2)分3步:
第1步:选1名医生,有3种选法.
第2步:选1名护士,有5种选法.
第3步:选1名麻醉师,有2种选法.
根据分步乘法计数原理,可知共有(种)不同的选法.
