第二十二章复习+测试

第二十二章节复习+测试
复习
1.二次函数的概念
一般地，形如　 　(a，b，c是常数，　 　__)的函数，叫做二次函数．
【注意】
(1)等号右边必须是整式；
(2)自变量的最高次数是2；
(3)当b＝0，c＝0时，y＝ax2是特殊的二次函数．
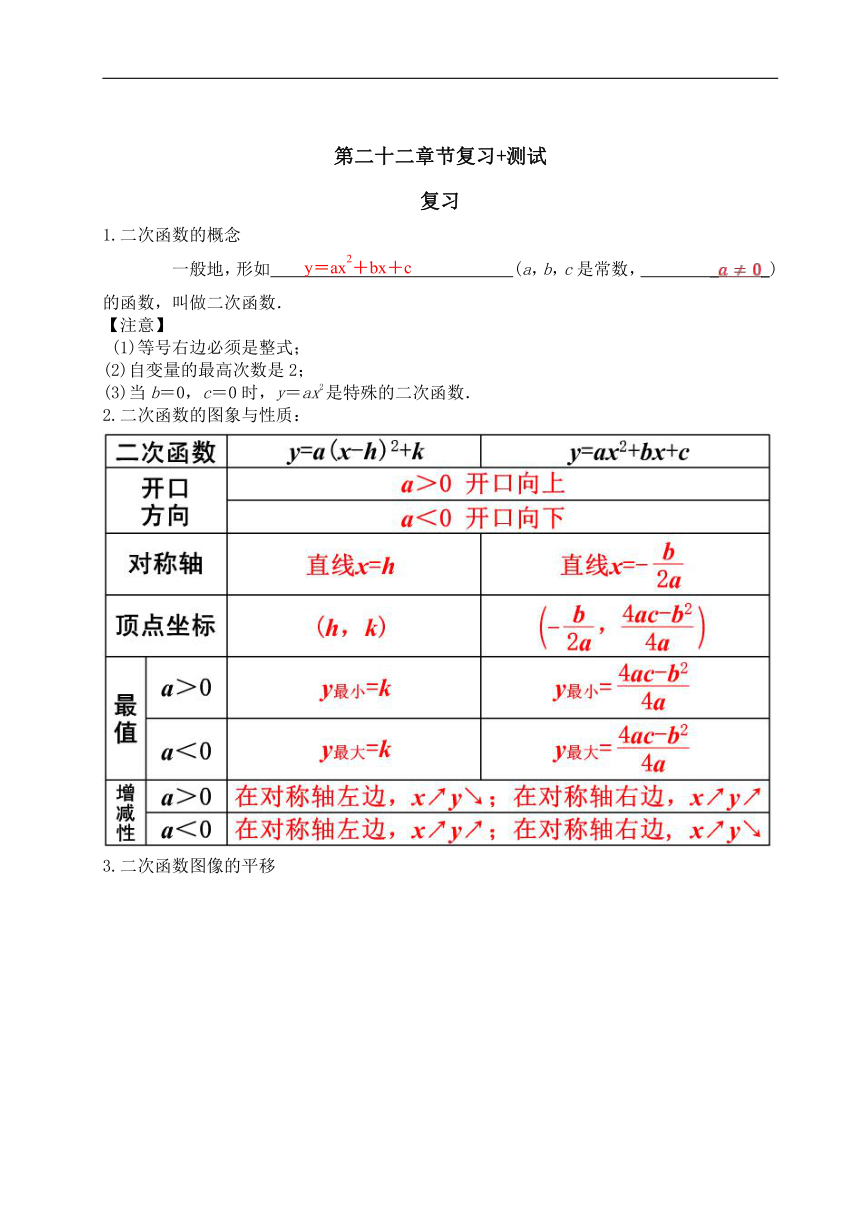
2.二次函数的图象与性质：
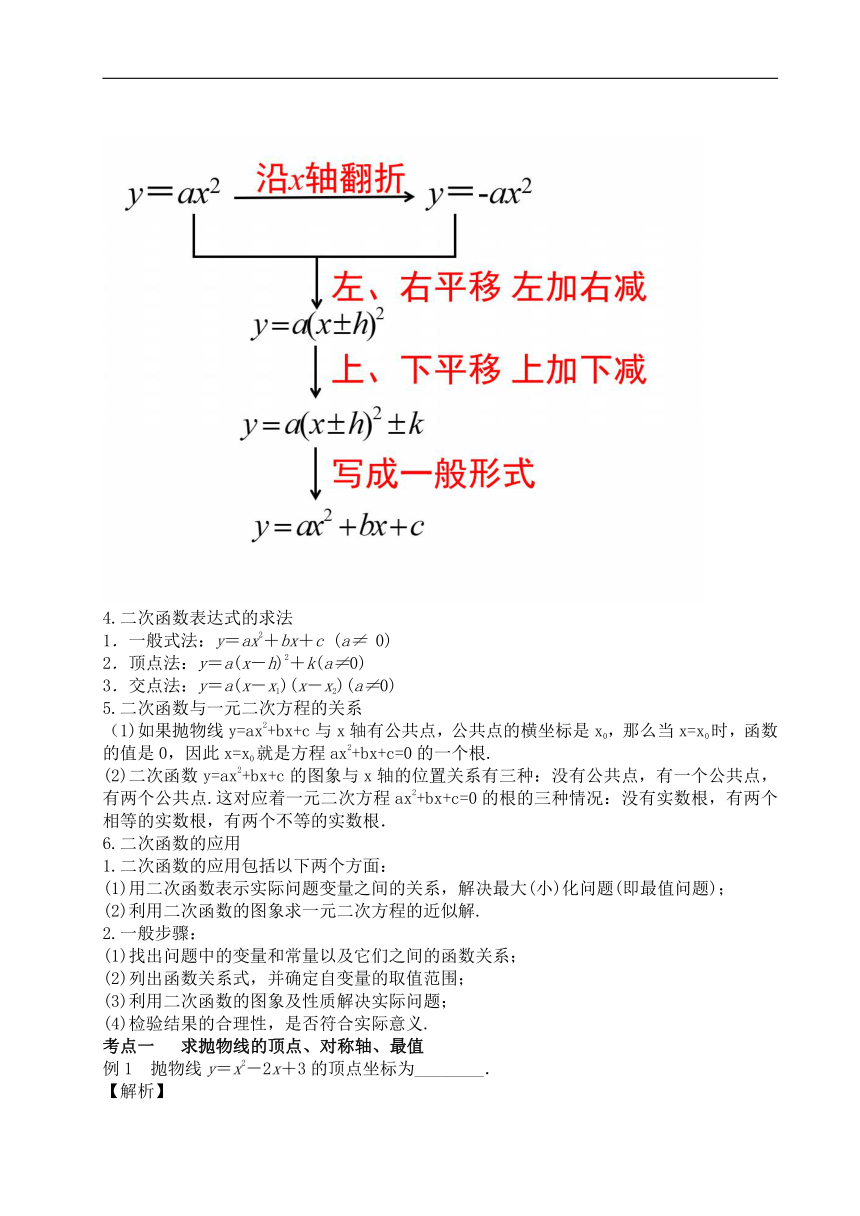
3.二次函数图像的平移
4.二次函数表达式的求法
1．一般式法：y＝ax2＋bx＋c (a≠ 0)
2．顶点法：y＝a(x－h)2＋k(a≠0)
3．交点法：y＝a(x－x1)(x－x2)(a≠0)
5.二次函数与一元二次方程的关系
（1)如果抛物线y=ax2+bx+c与x轴有公共点，公共点的横坐标是x0，那么当x=x0时，函数的值是0，因此x=x0就是方程ax2+bx+c=0的一个根.
(2)二次函数y=ax2+bx+c的图象与x轴的位置关系有三种：没有公共点，有一个公共点，有两个公共点.这对应着一元二次方程ax2+bx+c=0的根的三种情况：没有实数根，有两个相等的实数根，有两个不等的实数根．
6.二次函数的应用
1.二次函数的应用包括以下两个方面：
(1)用二次函数表示实际问题变量之间的关系，解决最大(小)化问题(即最值问题)；
(2)利用二次函数的图象求一元二次方程的近似解.
2.一般步骤：
(1)找出问题中的变量和常量以及它们之间的函数关系；
(2)列出函数关系式，并确定自变量的取值范围；
(3)利用二次函数的图象及性质解决实际问题；
(4)检验结果的合理性，是否符合实际意义.
考点一 求抛物线的顶点、对称轴、最值
例1 抛物线y＝x2－2x＋3的顶点坐标为________．
【解析】
方法一：配方，得y＝x2－2x＋3＝(x－1)2＋2，则顶点坐标为(1,2)．
方法二代入公式 ，，
则顶点坐标为(1,2)．
【方法归纳】:解决此类题目可以先把二次函数y＝ax2＋bx＋c配方为顶点式y＝a(x－h)2＋k的形式，得到：对称轴是直线x＝h，最值为y＝k，顶点坐标为(h，k)；也可以直接利用公式求解.
考点二 二次函数的图像与性质及函数值的大小比较
例2 二次函数y＝－x2＋bx＋c的图像如图所示，若点A(x1，y1)，B(x2，y2)在此函数图像上，且x1A. y1≤y2 B．y1C．y1≥y2 D．y1>y2
【解析】由图像看出，抛物线开口向下，对称轴是x＝1，当x＜1时，y随x的增大而增大．
∵x1考点三 二次函数 y＝ax2＋bx＋c(a≠0)的图像与系数a，b，c的关系
例3 已知二次函数y＝ax2＋bx＋c的图像如图所示，下列结论：①abc＞0；②2a－b＜0；③4a－2b＋c＜0；④(a＋c)2＜b2. 其中正确的个数是(　　)
A．1　　　B．2　　　　　C．3　　　　　D．4
【解析】：由图像开口向下可得a＜0，由对称轴在y轴左侧可得b＜0，由图像与y轴交于正半轴可得 c＞0，则abc＞0，故①正确；
由对称轴x>－1可得2a－b＜0，故②正确；
由图像上横坐标为 x＝－2的点在第三象限可得4a－2b＋c＜0，故③正确；
由图像上横坐标为x＝1的点在第四象限得出a＋b＋c＜0，由图像上横坐标为x＝－1的点在第二象限得出
a－b＋c＞0，则(a＋b＋c)(a－b＋c)＜0，
即(a＋c)2－b2＜0，可得(a＋c)2＜b2，
故④正确．故选D.
【方法总结】
1.可根据对称轴的位置确定b的符号：b＝0 对称轴是y轴；a、b同号 对称轴在y轴左侧；a、b异号 对称轴在y轴右侧.这个规律可简记为“左同右异”.
2.当x＝1时，函数y＝a＋b＋c.当图像上横坐标
x＝1的点在x轴上方时，a＋b＋c＞0；当图像上横坐标x＝1的点在x轴上时，a＋b＋c＝0；当图像上横坐标x＝1的点在x轴下方时，a＋b＋c＜0.同理，可由图像上横坐标x＝－1的点判断a－b＋c的符号.
考点四 抛物线的几何变换
例4 将抛物线y＝x2－6x＋5向上平移 2个单位长度，再向右平移1个单位长度后，得到的抛物线解析式是(　　)
A．y＝(x－4)2－6 B．y＝(x－4)2－2
C．y＝(x－2)2－2 D．y＝(x－1)2－3
【解析】因为y＝x2－6x＋5＝(x－3)2－4，所以向上平移2个单位长度，再向右平移1个单位长度后，得到的解析式为y＝(x－3－1)2－4＋2，即y＝ (x－4)2－2.故选B.
考点五 二次函数表达式的确定
例5.已知抛物线y=ax2+bx+c与抛物线y=－x2－3x+7的形状相同,顶点在直线x=1上,且顶点到x轴的距离为5,请写出满足此条件的抛物线的表达式.
解:抛物线y=ax2+bx+c与抛物线y=－x2－3x+7的形状
相同 a=1或－1
又顶点在直线x=1上,且顶点到x轴的距离为5,
顶点为(1,5)或(1,－5)
所以其表达式为:
(1) y=(x－1)2+5 (2) y=(x－1)2－5
(3) y=－(x－1)2+5 (4) y=－(x－1)2－5
考点六 二次函数与一元二次方程
例6 若二次函数y=x2+mx的对称轴是x=3，则关于x的方程x2+mx=7的解为（　　）
A．x1=0，x2=6 B．x1=1，x2=7
C．x1=1，x2=﹣7 D．x1=﹣1，x2=7
【解析】：∵二次函数y=x2+mx的对称轴是x=3，
∴ =3，解得m=－6，
∴关于x的方程x2+mx=7可化为x2－6x－7=0，
即(x+1)(x－7)=0，解得x1=－1，x2=7．
故选D．
考点七 二次函数的应用
例7 某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于45%，经试销发现，销售量y(件)与销售单价x(元)符合一次函数y＝kx＋b，且x＝65时，y＝55；x＝75时，y＝45.
(1)求一次函数的表达式；
(2)若该商场获得利润为w元，试写出利润w与销售单价x之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？
解：(1)根据题意，得，解得
故所求一次函数的表达式为y=-x+120.
(2)w=(x-60)(-x+120)=-x2+180x-7200，配方得w=-(x-90)2+900
∵ 抛物线的开口向下
∴ 当x＜90时，w随x的增大而增大
∵ 60≤x≤60×(1+45%)，即60≤x≤87
∴ 当x=87时，w有最大值，此时w=-(87-90)2+900=891
故销售单价定为87元时，商场可获得最大利润891元.
例8.一家电脑公司推出一款新型电脑，投放市场以来3个月的利润情况如图所示，该图可以近似看作为抛物线的一部分，请结合图象，解答以下问题：
(1)求该抛物线对应的二次函数解析式；
(2)该公司在经营此款电脑过程中，第几月的利润最大？最大利润是多少？
(3)若照此经营下去，请你结合所学的知识，对公司在此款电脑的经营状况(是否亏损？何时亏损？)作预测分析.
解：(1)因图象过原点，则设函数解析式为y=ax2+bx，
由图象的点的含义，得，解得
故所求一次函数的表达式为y=-x2+14x
(2)y=-x2+14x=-(x-7)2+49
∴ 当x=7时，y最大=49
故第7个月时，利润最大为49万元.
(3)没有利润，即-x2+14x=0解得x1=0(舍去)或x2=14
而这时利润为滑坡状态，所以第15个月，公司亏损.
测试
一、选择题
1.抛物线=2﹣6+5的顶点坐标为
A、（3，﹣4） B、（3，4） C、（﹣3，﹣4） D、（﹣3，4）
【答案】A。
【分析】利用配方法把抛物线的一般式写成顶点式，求顶点坐标，或者用顶点坐标公式求解：
∵=2﹣6+5=2﹣6+9﹣9+5=（﹣3）2﹣4，∴抛物线=2+6+5的顶点坐标是（3，﹣4）．故选A。
【考点】二次函数的性质。
2.在平直角坐标系中，如果抛物线y＝4x2不动，而把x轴、y轴分别向上、向右平移2个单位，那么在新坐标系下抛物线的解析式是（ ）
A. y＝4（x﹣2）2+2 B. y＝4（x+2）2﹣2
C. y＝4（x﹣2）2﹣2 D. y＝4（x+2）2+2
【答案】B
【分析】将x轴向上平移2个单位就相当于将抛物线向下平移2个单位，将y轴向右平移就相当于将抛物线向左平移2个单位，据此根据平面直角坐标系中函数图象的平移规律求解可得．
【解析】将x轴向上平移2个单位就相当于将抛物线向下平移2个单位，
将y轴向右平移就相当于将抛物线向左平移2个单位，根据平移法则：左加右减，上加下减，
∴在新坐标系下抛物线的解析式为y＝4（x+2）2﹣2，故选：B．
【点睛】本题主要考查了二次函数图像的平移，掌握平移规律：左加右减，上加下减是解题的关键．
3、一个二次函数的图象的顶点坐标为（3，-1）与y轴的交点（0，-4）这个二次函数的解析式是（ ）
A． B．
C． D．
【答案】B．
【解析】∵二次函数的图象的顶点坐标是（3，－1），∴设这个二次函数的解析式为，
把（0，﹣4）代入得，∴这个二次函数的解析式为．故选B．
【考点】待定系数法求二次函数解析式．
4．已知函数（a是常数，），下列结论正确的是（ ）
A．当a＝1时，函数图象经过点（－1，0） B．当a＝－2时，函数图象与x轴没有交点
C．若a<0，函数图象的顶点始终在x轴的下方 D．若a>0，则当时，y随x的增大而增大
【答案】D，
【解析】A、当a＝1时，函数解析式为y＝x2－2x－1，当x＝－1时，y＝1＋2－1＝2，
∴当a＝1时，函数图象经过点（－1，2），∴A选项不符合题意；
B、当a＝2时，函数解析式为y＝－2x2＋4x－1，令y＝－2x2＋4x－1＝0，则△＝42－4×（－2）×（－1）＝8＞0，∴当a＝－2时，函数图象与x轴有两个不同的交点，∴B选项不符合题意；
C、∵y＝ax2－2ax－1＝a（x－1）2－1－a，∴二次函数图象的顶点坐标为（1，－1－a），当－1－a＜0时，有a＞－1，∴C选项不符合题意；
D、∵y＝ax2－2ax－1＝a（x－1）2－1－a，∴二次函数图象的对称轴为x＝1．若a＞0，则当x≥1时，y随x的增大而增大，∴D选项符合题意．故选D．
【考点】二次函数的性质。
5、已知二次函数y＝（x﹣a﹣1）（x﹣a+1）﹣3a+7（其中x是自变量）的图象与x轴没有公共点，且当x＜﹣1时，y随x的增大而减小，则实数a的取值范围是（　　）
A．a＜2 B．a＞﹣1 C．﹣1＜a≤2 D．﹣1≤a＜2
【答案】D．
【解析】y＝（x﹣a﹣1）（x﹣a+1）﹣3a+7＝x2﹣2ax+a2﹣3a+6，
∵抛物线与x轴没有公共点，
∴△＝（﹣2a）2﹣4（a2﹣3a+6）＜0，解得a＜2，
∵抛物线的对称轴为直线x＝﹣＝a，抛物线开口向上，
而当x＜﹣1时，y随x的增大而减小，∴a≥﹣1，
∴实数a的取值范围是﹣1≤a＜2．故选：D．
【考点】二次函数对称轴综合问题．
6．如图，将函数＝的图像沿轴向上平移得到一条新函数的图像，其中点A（1，）、B（4，）平移后的对应点分别为点A′、B′．若曲线段AB扫过的面积为9（图中的阴影部分），则新图像的函数表达式是（ ）
A．＝ B．＝
C．＝ D．＝
【答案】D，
【解析】连接AB、A′B′，则S阴影＝S四边形ABB′A′．由平移可知，AA′＝BB′，AA′∥BB′，
所以四边形ABB′A′是平行四边形．分别延长A′A、B′B交轴于点M、N．
因为A（1，）、B（4，），所以MN＝4－1＝3．
因为＝AA′·MN，所以9＝3AA′，解得AA′＝3，
即沿轴向上平移了3个单位，所以新图像的函数表达式＝．故答案选D
【考点】二次函数与几何综合问题．
二、填空题
1.下列说法中正确的序号是
①在函数y=﹣x2中，当x=0时y有最大值0；②在函数y=2x2中，当x＞0时y随x的增大而增大
③抛物线y=2x2，y=﹣x2，y=﹣中，抛物线y=2x2开口最小，抛物线y=﹣x2的开口最大
④不论a是正数还是负数，抛物线y=ax2的顶点都是坐标原点
【答案】①②④
【解析】由函数的解析式y＝－x2，可知a=-1＜0，得到函数的开口向下，有最大值y=0，故①正确；
由函数的解析式y＝2x2，可知其对称轴为y轴，对称轴的左边（x＜0），y随x增大而减小，对称轴的右边（x＞0），y随x增大而增大，故②正确；
根据二次函数的性质，可知系数a决定开口方向和开口大小，且a的值越大开口越小，可知抛物线y＝2x2的开口最小，抛物线y＝－x2的开口第二小，而y开口最大，故③不正确；
不论a是正数还是负数，抛物线y＝ax2的顶点都是坐标原点，④正确.
故选C.
【点睛】：此题主要考查了二次函数的图像与性质，解题关键是明确y=ax2的图像的特点，直接按断即可.
2．把二次函数y=x2﹣2x+3的图象绕原点旋转180°后得到的图象的函数解析式为　 　．
【答案】y=﹣x2﹣2x﹣3．
【分析】求出原抛物线的顶点坐标以及绕原点旋转180°后的抛物线的顶点坐标，再根据旋转后抛物线开口方向向下，利用顶点式解析式写出即可．
【解答】解：∵抛物线y=x2﹣2x+3=（x﹣1）2+2的顶点坐标为（1，2），
∴绕原点旋转180°后的抛物线的顶点坐标为（﹣1，﹣2），
∴所得到的图象的解析式为y=﹣（x+1）2﹣2，即y=﹣x2﹣2x﹣3．
故答案为y=﹣x2﹣2x﹣3．
【点评】本题考查了二次函数图象与几何变换，利用顶点的变化确定函数解析式的变化更简便．
3.已知二次函数（为常数），当取不同的值时，其图象构成一个“抛物线系”．如图分别是当取四个不同数值时此二次函数的图象．发现它们的顶点在同一条直线上，那么这条直线的表达式是_________．
【答案】
【分析】已知抛物线的顶点式，写出顶点坐标，用x、y代表顶点的横坐标、纵坐标，消去a得出x、y的关系式．
【解析】二次函数中，顶点坐标为：，设顶点坐标为（x，y），
∴①，②，
由①2+②，得，∴；
故答案为：.
【点睛】本题考查了二次函数的性质，根据顶点式求顶点坐标的方法是解题的关键，注意运用消元的思想解题．
4.如图，在边长为6cm的正方形ABCD中，点E、F、G、H分别从点A、B、C、D同时出发，均以1cm/s的速度向点B、C、D、A匀速运动，当点E到达点B时，四个点同时停止运动，在运动过程中，当运动时间为______s时，四边形EFGH的面积最小，其最小值是________cm2．
【答案】 (1). 3 (2). 18
【解析】设运动时间为t（0≤t≤6），则AE=t，AH=6﹣t，
根据题意得：S四边形EFGH=S正方形ABCD﹣4S△AEH=6×6﹣4×t（6﹣t）=2t2﹣12t+36=2（t﹣3）2+18，
∴当t=3时，四边形EFGH的面积取最小值，最小值为18．
【考点】二次函数的最值；正方形的性质．
5.二次函数的部分图象如图所示， 图象过点(－1，0)，对称轴为直线＝2，则下列结论中正确的序号是 。①4＋b＝0； ②；③若点A(－3，)，点B(－，)，点C(5，)在该函数图象上，则＜＜；④ 若方程的两根为和，且＜，则＜－1＜5＜
【答案】①③④
【解析】由抛物线的对称轴为x=2可得-=2，即4a+b=0，故①正确；
由抛物线的对称性知x=0和x=4时，y＞0，则x=3时，y=9a+3b+c＞0，故②错误；
∵抛物线的开口向下，且对称轴为x=2，∴抛物线上离对称轴水平距离越小，函数值越大，
∵点A到x=2的水平距离为5，点B到对称轴的水平距离为2.5，点C到对称轴的水平距离为3，
∴y1＜y3＜y2，故③正确；
令y=a（x+1）（x-5），则抛物线y=a（x+1）（x-5）与y=ax2+bx+c形状相同、开口方向相同，且与x轴的交点为（-1，0）、（3，0），函数图象如图所示，
由函数图象可知方程a（x+1）（x-5）=-3的两根即为抛物线y=a（x+1）（x-5）与直线y=-3交点的横坐标，∴x1＜-1＜5＜x2，故④正确；
故答案①③④
三、解答题
1.某商店经销《超级飞侠》 “乐迪”玩具，“乐迪”玩具每个进价60元，每个玩具不得低于80元出售．销售“乐迪”玩具的单价 (元/个)与销售数量 (个)之间的函数关系如图所示．
（1）试解释线段AB所表示的实际优惠销售政策；
（2）写出该店当一次销售 ( ＞10)个时，所获利润 （元）与 （个）之间的函数关系式；
（3）店长经过一段时间的销售发现：卖25个赚的钱反而比卖30个赚的钱多，你能用数学知识解释这一现象吗？为了不出现这种现象，在其他条件不变的情况下，店长应把最低价每个80元至少提高到多少元？
【分析】（1）利用待定系数法求线段AB的函数的解析式，设m=kx+b，把A（10，100）和B（30，80）代入上式得到关于k、b的方程组，解方程组求出解析式；然后根据解析式解释线段AB所表示的实际优惠销售政策即可。
（2）分类讨论：当10（3）先将W=-n2+50n化成顶点式，根据二次函数的性质讨论增减性，可得出答案。
【解析】（1）解：(1)设m=kx+b，
把A(10,100)和B(30,80)代入上式，得
解之：
∴线段AB的函数的解析式为m= n+110(10≤n≤30)；
由解析式可知线段AB所表示的实际优惠销售政策：一次性销售10到30个时，每多销售1个，玩具的单价下降1元.
（2）解：(2)当10当n≤30时,W=(80 60)n=20n.
（3）解：(3)W= n2+50n= (n 25)2+625，
①当10②当25∴卖25个赚的钱反而比卖30个赚的钱多。∴当n=25时，m= n+110=85，
∴当每个玩具不得低于85元时，n的位置范围为102.如图，平面直角坐标系中，抛物线交轴于点A．P为抛物线上一点，且与点A不重合．连结AP，以AO、AP为邻边作平行四边形OAPQ，PQ所在直线与轴交于点B．设点P的横坐标为．（1）点Q落在x轴上时m的值．（2）若点Q在轴下方，则为何值时，线段BQ的长取最大值，并求出这个最大值．
【分析】（1）可以令=0可得点A坐标为（0，3），当Q落在轴上时，PQ=OA=3，即可得出y=3时m的值。
（2）根据当PB取最小值时，QB最大，当=2时，二次函数= 2－2＋3有最小值即可得出答案。
【答案】解：（1）令=0可得点A坐标为（0，3），当Q落在轴上时，PQ=OA=3。
在= 2－2＋3中，令=3可求得点P横坐标m=4。
（2）∵QB=OA-PB=3-PB，∴当PB取最小值时，QB最大。
当=2时，二次函数= 2－2＋3有最小值y=1。
∴当m=2时，QB的最大值为2。
【考点】二次函数综合题，点的坐标与方程的关系，二次函数的性质。
3.受“新冠”疫情的影响，某销售商在网上销售、两种型号的“手写板”，获利颇丰．已知型，型手写板进价、售价和每日销量如表格所示：
进价（元/个） 售价（元/个） 销量（个/日）
型
型
根据市场行情，该销售商对型手写板降价销售，同时对型手写板提高售价，此时发现型手写板每降低元就可多卖个，型手写板每提高元就少卖个，要保持每天销售总量不变，设其中型手写板每天多销售个，每天总获利的利润为元
（1）求与之间的函数关系式并写出的取值范围；
（2）要使每天的利润不低于元，直接写出的取值范围；
（3）该销售商决定每销售一个型手写板，就捐元给因“新冠疫情”影响的困难家庭，当时，每天的最大利润为元，求的值．
【答案】（1）（），且x为整数；（2），且x为整数；（3）
【分析】（1）设型手写板每天多销售个，则B型手写板每天少销售个，根据总获利的利润等于销售A型手写板所获利润加上销售B型手写板所获利润，根据每件销售的利润，每日的销量都为非负数且为非负整数求出x的取值范围；
（2）结合（1）将总利润函数进行配方，求出当时的x值，结合图象得到每天的利润不低于元时的x的取值范围，进而求解；
（3）设捐款后每天的利润为元，则，然后利用二次函数的性质进行求解．
【解析】（1） ，
化简得，，由题意知，，解得，，
故的取值范围为且为整数；
（2）的取值范围为，
理由如下：，
当时，，
∴，，∴或，
要使，由图象知，；
，，且为整数；
（3）设捐款后每天的利润为元，
则，
对称轴为，
，，
抛物线开口向下，当时，随的增大而增大，
当时，最大，，
解得，．
【点睛】本题考查二次函数的应用，正确理解题意，列出二次函数的表达式是解题的关键，第（2）（3）题可结合二次函数的图象进行求解．
4.受“新冠”疫情的影响，某销售商在网上销售、两种型号的“手写板”，获利颇丰．已知型，型手写板进价、售价和每日销量如表格所示：
进价（元/个） 售价（元/个） 销量（个/日）
型
型
根据市场行情，该销售商对型手写板降价销售，同时对型手写板提高售价，此时发现型手写板每降低元就可多卖个，型手写板每提高元就少卖个，要保持每天销售总量不变，设其中型手写板每天多销售个，每天总获利的利润为元
（1）求与之间的函数关系式并写出的取值范围；
（2）要使每天的利润不低于元，直接写出的取值范围；
（3）该销售商决定每销售一个型手写板，就捐元给因“新冠疫情”影响的困难家庭，当时，每天的最大利润为元，求的值．
【答案】（1）（），且x为整数；（2），且x为整数；（3）
【分析】（1）设型手写板每天多销售个，则B型手写板每天少销售个，根据总获利的利润等于销售A型手写板所获利润加上销售B型手写板所获利润，根据每件销售的利润，每日的销量都为非负数且为非负整数求出x的取值范围；
（2）结合（1）将总利润函数进行配方，求出当时的x值，结合图象得到每天的利润不低于元时的x的取值范围，进而求解；
（3）设捐款后每天的利润为元，则，然后利用二次函数的性质进行求解．
【解析】（1） ，
化简得，，由题意知，，解得，，
故的取值范围为且为整数；
（2）的取值范围为，
理由如下：，
当时，，
∴，，∴或，
要使，由图象知，；
，，且为整数；
（3）设捐款后每天的利润为元，
则，
对称轴为，
，，
抛物线开口向下，当时，随的增大而增大，
当时，最大，，
解得，．
【点睛】本题考查二次函数的应用，正确理解题意，列出二次函数的表达式是解题的关键，第（2）（3）题可结合二次函数的图象进行求解．
y＝ax2＋bx＋c