第二十三章复习+测试

第二十三章复习+测试
复习
一、旋转的特征
1．旋转过程中，图形上每一点都绕旋转中心按同一旋转方向旋转同样大小的角度．
2．任意一对对应点与旋转中心的连线所成的角都是
旋转角，对应点到旋转中心的距离都相等．
3．旋转前后对应线段、对应角分别相等，图形的大小、形状不变．
二、中心对称
1．中心对称
把一个图形绕着某一个点旋转180°，如果它能与另一个图形重合，那么就说这两个图形成中心对称，这个点叫做对称中心，这两个图形中的对应点叫做关于中心的对称点．
2．中心对称的特征
中心对称的特征：在成中心对称的两个图形中，对应点所连线段都经过对称中心，并且被对称中心平分．
3.中心对称图形
把一个图形绕某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形，这个点叫做它的对称中心．
考点一 旋转的概念及性质的应用
例1 （1）如图a，将三角形AOB绕点O按逆时针方
向旋转60 °后得到三角形COD，若∠AOB=15 °,
则∠AOD的度数是（ ）
A. 15 ° B. 60 °
C. 45 ° D. 75 °
【解析】关键找出旋转角∠BOD=60 °;
【方法总结】
(1)画旋转后的图形，要善于抓住图形特点，作出特殊点的对应点；
(2)旋转作图时要明确三个方面：旋转中心、旋转角度及旋转方向(顺时针或逆时针)．
考点二 旋转变换
例2 如图，在Rt△ABC中，∠ACB=90°，点D，E分别在AB，AC上，CE=BC，连接CD，将线段CD绕点C按顺时针方向旋转90°后得CF，连接EF．
（1）补充完成图形；
（2）若EF∥CD，求证：∠BDC=90°．
【解析】：（1）根据题意，找准旋转中心，旋转方向及旋转角度，补全图形即可；
（2）由旋转的性质得∠DCF为直角，由EF与CD平行，得到∠EFC为直角，利用SAS得到△BDC与△EFC全等，利用全等三角形对应角相等即可得证．
解：（1）补全图形，如图所示；
（2）由旋转的性质得，DC=FC，∠DCF=90°，
∴∠DCE+∠ECF=90°.
∵∠ACB=90°，
∴∠DCE+∠BCD=90°，
∴∠ECF=∠BCD，
∵EF∥DC，
∴∠EFC+∠DCF=180°，
∴∠EFC=90°，
∴△BDC≌△EFC（SAS），
∴∠BDC=∠EFC=90°．
考点三 中心对称
例3 下列图形中，既不是轴对称图形，也不是中心对称图形的是( )
【方法总结】
中心对称图形和轴对称图形的主要区别在于一个是绕一点旋转，另一个是沿一条直线对折.这是易错点，也是辨别它们不同的关键.
考点四 图形变换的简单应用
例6：如图所示的图案是一个轴对称图形(不考虑颜色)，直线m是它的一条对称轴.已知图中圆的半径为r,求你能借助轴对称的方法求出图中阴影部分的面积吗？说说你的做法.
解：以直线m为对称轴，把m左边绿色部分反射到m的右边，那么它们的像恰好填补了右边的白色部分，所以图中的绿色部分面积等于半个圆的面积，也就是 .
测试
一、选择题
1．下列图形是我国国产品牌汽车的标识，其中是中心对称图形的是
A． B． C． D．
【答案】C
【解析】A、不是中心对称图形，本选项错误；
B、不是中心对称图形，本选项错误；
C、是中心对称图形，本选项正确；
D、不是中心对称图形，本选项错误．故选C．
【点睛】本题考查了中心对称图形的概念．中心对称图形是要寻找对称中心，旋转180°后两部分重合．
2.将如图所示的图形按逆时针方向旋转90 后得到图形是（ ）
A. B. C. D.
【答案】A
【分析】根据旋转的定义，观察图形即可解答.
【解析】根据旋转的定义，图片按逆时针方向旋转90°，箭头竖直向下，从而可确定为A图．
故选A．
【点睛】本题主要考查了旋转的性质，熟知性质是解题的关键.
3.如图，将△ABC绕点A顺时针旋转 60°得到△AED，若AB=4，AC=3，BC=2，则BE的长为（ ）
A. 5 B. 4 C. 3 D. 2
【答案】B
【分析】根据将△ABC绕点A顺时针旋转 60°得到△AED可得△ABE是等边三角形，根据等边三角形的性质即可得.
【解析】∵将△ABC绕点A顺时针旋转 60°得到△AED，
∴AE=AB，∠BAE=60°，∴△ABE是等边三角形，∴BE=AB=4，故选B.
【点睛】本题考查了旋转的性质、等边三角形的判定与性质，得出△ABE是等边三角形是解题的关键.
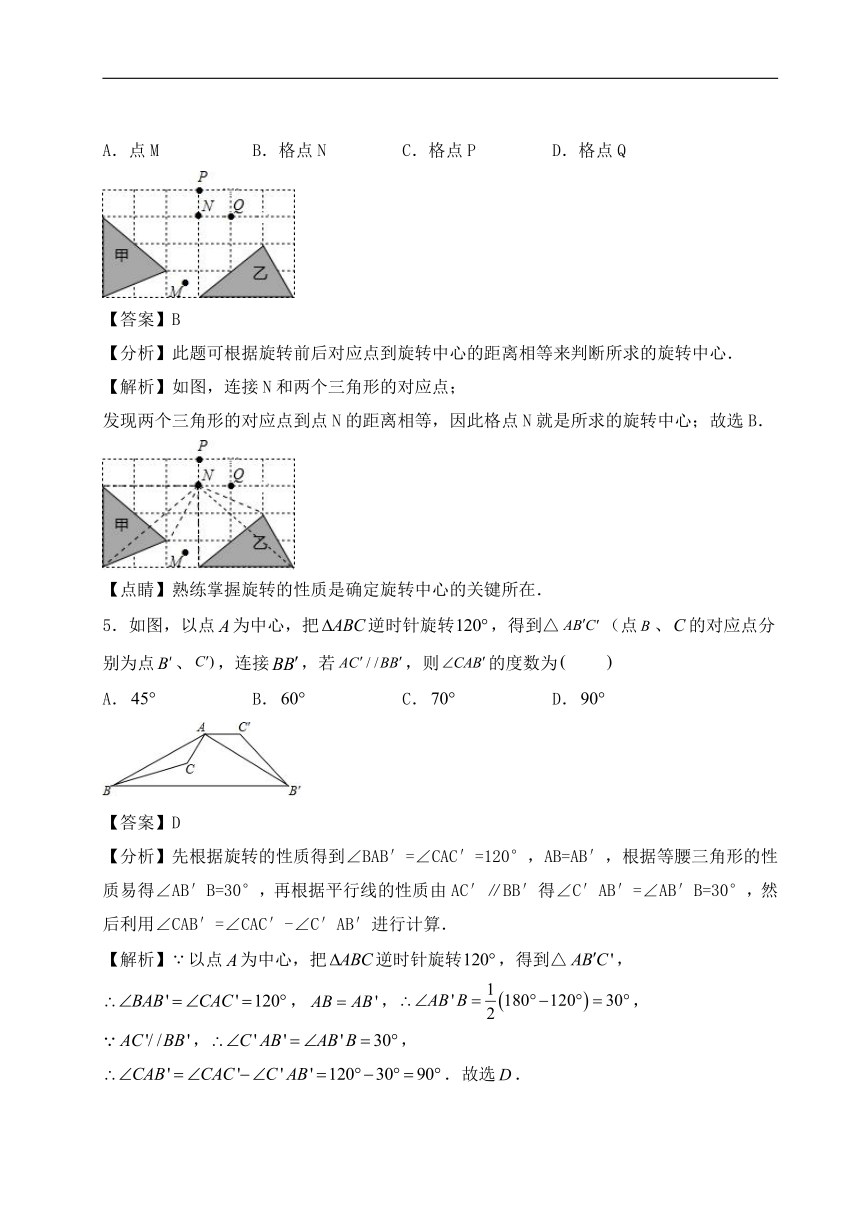
4．如图，在6×4的方格纸中，格点三角形甲经过旋转后得到格点三角形乙，则其旋转中心是（ ）
A．点M B．格点N C．格点P D．格点Q
【答案】B
【分析】此题可根据旋转前后对应点到旋转中心的距离相等来判断所求的旋转中心．
【解析】如图，连接N和两个三角形的对应点；
发现两个三角形的对应点到点N的距离相等，因此格点N就是所求的旋转中心；故选B．
【点睛】熟练掌握旋转的性质是确定旋转中心的关键所在．
5．如图，以点为中心，把逆时针旋转，得到△（点、的对应点分别为点、，连接，若，则的度数为　　
A． B． C． D．
【答案】D
【分析】先根据旋转的性质得到∠BAB′=∠CAC′=120°，AB=AB′，根据等腰三角形的性质易得∠AB′B=30°，再根据平行线的性质由AC′∥BB′得∠C′AB′=∠AB′B=30°，然后利用∠CAB′=∠CAC′-∠C′AB′进行计算．
【解析】以点为中心，把逆时针旋转，得到△，
，，，
，，
．故选．
【点睛】本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线的夹角等于旋转角．也考查了等腰三角形的性质，三角形内角和定理以及平行线的性质．
6．将一副三角板顶点重合，三角板ABC绕点A顺时针转动的过程中，∠EAB度数符合下列条件时，三角尺不存在一组边平行的是（三角板边AB＝AE）（　　）
A．∠EAB＝30° B．∠EAB＝45° C．∠EAB＝60° D．∠EAB＝75°[]
【答案】C
【分析】由旋转的性质和平行线的判定依次判断，可求解．
【解析】当∠EAB=30°时．
∵∠CAB=90°，∴∠CAE=60°=∠E，∴AC∥DE，故A不合题意；
当∠EAB=45°，∴∠BAD=45°=∠B，∴BC∥AD，故B不合题意；
当∠EAB=60°时，三角尺不存在一组边平行．
当∠EAB=75°时，如图，延长AB交DE于点M，∴∠BAD=15°，
∴∠EMA=∠D+∠MAB=45°=∠ABC，∴BC∥DE．故选C．
【点睛】本题考查了旋转的性质，平行线的判定，熟练运用旋转的性质是本题的关键．
二、填空题
1．如图，将Rt△ABC的斜边AB绕点A顺时针旋转α（0°<α<90°）得到AE，直角边AC绕点A逆时针旋转β（0°<β<90°）得到AF，连接EF．若AB=3，AC=2，且α+β=∠B，则EF=__________．
【答案】
【解析】由旋转的性质可得AE=AB=3，AC=AF=2，
∵∠B+∠BAC=90°，且α+β=∠B，∴∠BAC+α+β=90°，
∴∠EAF=90°，∴EF==，
故答案为：．
【点睛】本题考查了旋转的性质，勾股定理，灵活运用旋转的性质是本题的关键．
2.将边长为1的正方形ABCD绕点C按顺时针方向旋转到FECG的位置（如图），使得点D落在对角线CF上，EF与AD相交于点H，则HD＝ 　．（结果保留根号）
【答案】﹣1．[]
【解析】∵四边形ABCD为正方形，∴CD＝1，∠CDA＝90°，
∵边长为1的正方形ABCD绕点C按顺时针方向旋转到FECG的位置，使得点D落在对角线CF上，
∴CF＝，∠CFDE＝45°，∴△DFH为等腰直角三角形，
∴DH＝DF＝CF﹣CD＝﹣1．故答案为﹣1．
【考点】本题主要考查了以正方形旋转为载体的求线段长度.
3．一副三角板如图放置，将三角板ADE绕点A逆时针旋转α（0°＜α＜90°），使得三角板ADE的一边所在的直线与BC垂直，则α的度数为__________．
【答案】15°或45°．
【解析】分情况讨论：
①当DE⊥BC时，∠BAD=75°，∴α=90°﹣∠BAD=15°；
②当AD⊥BC时，∠BAD=45°，即α=45°．
故答案为：15°或45°．
【点睛】本题主要考查了垂直的定义，旋转的定义以及一副三角板的各个角的度数，理清定义是解答本题的关键．
4．如图，在△ABC中，∠BAC=90°，AB=AC=10cm，点D为△ABC内一点，∠BAD=15°，AD=6cm，连接BD，将△ABD绕点A按逆时针方向旋转，使AB与AC重合，点D的对应点为点E，连接DE，DE交AC于点F，则CF的长为__________cm．
【答案】10–2
【解析】如图，过点A作AG⊥DE于点G，由旋转知：AD=AE，∠DAE=90°，∠CAE=∠BAD=15°，∴∠AED=∠ADG=45°，
在△AEF中，∠AFD=∠AED+∠CAE=60°，在Rt△ADG中，AG=DG==3，
在Rt△AFG中，GF==，AF=2FG=2，∴CF=AC–AF=10–2，
故答案为：10–2．
【点睛】本题考查了旋转的性质，等腰直角三角形的性质，解直角三角形等，解题的关键是能够通过作适当的辅助线构造特殊的直角三角形，通过解直角三角形来解决问题．
5.如图，△ABC、△BDE都是等腰直角三角形，BA＝BC，BD＝BE，AC＝4，DE＝2．将△BDE绕点B逆时针方向旋转后得△BD′E′，当点E′恰好落在线段AD′上时，则CE′＝　　 ．
【解析】如图，连接CE′，
∵△ABC、△BDE都是等腰直角三角形，BA＝BC，BD＝BE，AC＝4，DE＝2，
∴AB＝BC＝2，BD＝BE＝2，
∵将△BDE绕点B逆时针方向旋转后得△BD′E′，
∴D′B＝BE′＝BD＝2，∠D′BE′＝90′，∠D′BD＝∠ABE′，
∴∠ABD′＝∠CBE′，∴△ABD′≌△CBE′（SAS），∴∠D′＝∠CE′B＝45°，
过B作BH⊥CE′于H，在Rt△BHE′中，BH＝E′H＝BE′＝，
在Rt△BCH中，CH＝＝，∴CE′＝+，
故答案为：．
三、解答题
1．（6分）如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，△OAB的三个顶点O（0，0）、A（4，1）、B（4，4）均在格点上．
（1）画出△OAB关于y轴对称的△OA1B1，并写出点A1的坐标；
（2）画出△OAB绕原点O顺时针旋转90°后得到的△OA2B2，并写出点A2的坐标；
（3）在（2）的条件下，求线段OA在旋转过程中扫过的面积（结果保留π）．
【解析】（1）如下图所示，点A1的坐标是（–4，1）；
（2）如下图所示，点A2的坐标是（1，–4）；
（3）∵点A（4，1），∴OA=，
∴线段OA在旋转过程中扫过的面积是：=．
【点睛】本题考查简单作图、扇形面积的计算、轴对称、旋转变换，解答本题的关键是明确题意，利用数形结合的思想解答．
2.△ABC在平面直角坐标系xOy中的位置如图所示．
（1）作△ABC绕点O逆时针旋转90°后的△A1B1C1．
（2）将△ABC向右平移3个单位，作出平移后的△A2B2C2．
（3）若点M是平面直角坐标系中直线AB上的一个动点，点N是x轴上的一个动点，且以O、A2、M、N为顶点的四边形是平行四边形，请直接写出点N的坐标．
【答案】（1）、（2）答案见解析；（3）当OA2为平行四边形的边时，N点坐标为（﹣3，0）或（2，0），当OA2为平行四边形的对角线时，N点坐标为（3，0）．
【分析】（1）利用网格特点和旋转的性质画出点A、B、C的对应点A1、B1、C1，从而得到△A1B1C1．
（2）利用网格特点和平移的性质画出点A、B、C的对应点A2、B2、C2，从而得到△A2B2C2．
（3）讨论：当OA2为平行四边形的边时，利用平行四边形的判定和点平移的坐标特征确定N点坐标；当OA2为平行四边形的对角线时，利用平行四边形的性质和点平移的坐标特征确定N点坐标．
【解析】（1）如图，△A1B1C1为所作；
（2）如图，△A2B2C2为所作；
（3）当OA2为平行四边形的边时，N点坐标为（﹣3，0）或（2，0），
当OA2为平行四边形的对角线时，N点坐标为（3，0）．
【点睛】本题考查了作图-旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了平移的性质和平行四边形的判定．
3.（8分）在Rt△ABC中，∠ABC=90°，∠ACB=30°，将△ABC绕点A顺时针旋转一定的角度α得到△DEC，点A、B的对应点分别是D、E．（1）当点E恰好在AC上时，如图1，求∠ADE的大小；（2）若α=60°时，点F是边AC中点，如图2，求证：四边形BEDF是平行四边形．
【解析】（1）如图1，∵△ABC绕点A顺时针旋转α得到△DEC，点E恰好在AC上，
∴CA=CD，∠ECD=∠BCA=30°，∠DEC=∠ABC=90°，
∵CA=CD，∴∠CAD=∠CDA=（180°–30°）=75°，∴∠ADE=90°–75°=15°；
（2）如图2，∵点F是边AC中点，∴BF=AC，
∵∠ACB=30°，∴AB=AC，∴BF=AB，∵△ABC绕点A顺时针旋转60得到△DEC，
∴∠BCE=∠ACD=60°，CB=CE，DE=AB，∴DE=BF，△ACD和△BCE为等边三角形，∴BE=CB，
∵点F为△ACD的边AC的中点，∴DF⊥AC，易证得△CFD≌△ABC，
∴DF=BC，∴DF=BE，而BF=DE，∴四边形BEDF是平行四边形．
【点睛】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了平行四边形的判定．
4．（8分）在平面直角坐标系中，四边形是矩形，点，点，点．以点为中心，顺时针旋转矩形，得到矩形，点的对应点分别为，记旋转角为．(1)如图①，当时，求点的坐标；(2)如图②，当点落在的延长线上时，求点的坐标；(3)当点落在线段上时，求点的坐标（直接写出结果即可）．
【答案】（1）点的坐标为；（2）点的坐标为；（3）点的坐标为．
【分析】(1) 过点作轴于根据已知条件可得出AD=6，再直角三角形ADG中可求出DG，AG的长，即可确定点D的坐标.
(2) 过点作轴于于可得出，根据勾股定理得出AE的长为10，再利用面积公式求出DH，从而求出OG,DG的长，得出答案
(3) 连接，作轴于G，由旋转性质得到，从而可证，继而可得出结论.
【解析】(1)过点作轴于，如图①所示：
点，点．，
以点为中心，顺时针旋转矩形，得到矩形，
，
在中，，
，点的坐标为；
(2)过点作轴于于，如图②所示：则，
，，
，，
，，
点的坐标为；
(3)连接，作轴于G，如图③所示：
由旋转的性质得：，
，，，
，，
在和中，，，
，，点的坐标为．
【点睛】本题考查的知识点是坐标系内矩形的旋转问题，用到的知识点有勾股定理，全等三角形的判定与性质等，做此类题目时往往需要利用数形结合的方法来求解，根据每一个问题做出不同的辅助线是解题的关键.