2024-2025学年北师大版九年级数学上册期中学情练习试卷(含答案)
文档属性
| 名称 | 2024-2025学年北师大版九年级数学上册期中学情练习试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 420.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-17 18:35:09 | ||
图片预览




文档简介
北师大版九年级数学第一学期期中学情练习试卷
一、选择题(共30分)
1. 关于x的一元二次方程 的一个根为0,则a的值为( )
A.2
B. 0
C.2或-2
D. -2
2. 若关于x的一元二次方程为 的解是x=1, 则2016-a-b的值是( )
A. 2018
B. 2011
C.2014
D.2021
3.某学习小组进行“用频率估计概率”的试验时,统计了某一结果出现的频率如下表,则符合这一结果的试验可能是( )
试验次数 100 200 500 800 1000 1200
试验频率 0.343 0.326 0.335 0.330 0.331 0.330
A.先后两次抛掷一枚质地均匀的硬币,两次都是反面朝上
B.先后两次抛掷一枚质地均匀的骰子,两次的点数和不大于6
C.将一个篮球和一个足球随机放入三个不同的篮子中,恰有一个篮子为空
D.从两男两女四人中抽取两人参加朗读比赛,两人性别相同
4.如果顺次连接四边形的各边中点得到的四边形是正方形,那么原来四边形的对角线一定满足的条件是( )
A.互相平分
B.相等
C.互相垂直
D.互相垂直且相等
5. 若关于x的一元二次方程ax ﹣2x+1=0有实数根,则实数a的取值范围是( )
A. a<1
B. a≤1
C. a≥1
D. a≤1且a≠0
6.等腰三角形三边长分别为a、b、4,且a、b是关于x的一元二次方程x -12x+k+2=0的两根,则k的值为( )
A. 30
B. 34或30
C. 36或30
D. 34
7.如图,在菱形ABCD中,∠D=135°,BE⊥CD于点E,交AC于点F,FG⊥BC于点G.若△BFG的周长为4,则菱形ABCD的面积为( )
A. 4
B. 8
C. 16
D. 16
8. 下列命题正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B. 对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形
D. 一组邻边相等的矩形是正方形
9.为了宣传垃圾分类,童威写了一篇倡议书,决定用微博转发的方式传播. 他设计了如下的传播规则:将倡议书发表在自己的微博上,再邀请n个好友转发,每个好友转发之后,又邀请n个互不相同的好友转发,依次类推. 已知经过两轮转发后,共有111个人参与了宣传活动,则n的值为( )
A.9
B.10
C.11
D.12
10. 如图所示, 在菱形ABCD中, 对角线AC与BD相交于点O, 交BC于点E, 则OE的长为( )
A. 6cm
B.4cm
C.3cm
D. 2cm
二、解答题。(共15分)
11. 已知a, b是 的两个根,则 +b= .
12.如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、AC、BC的中点,点P为线段EF上一个动点, 连接BP、GP, 则 的周长的最小值是 .
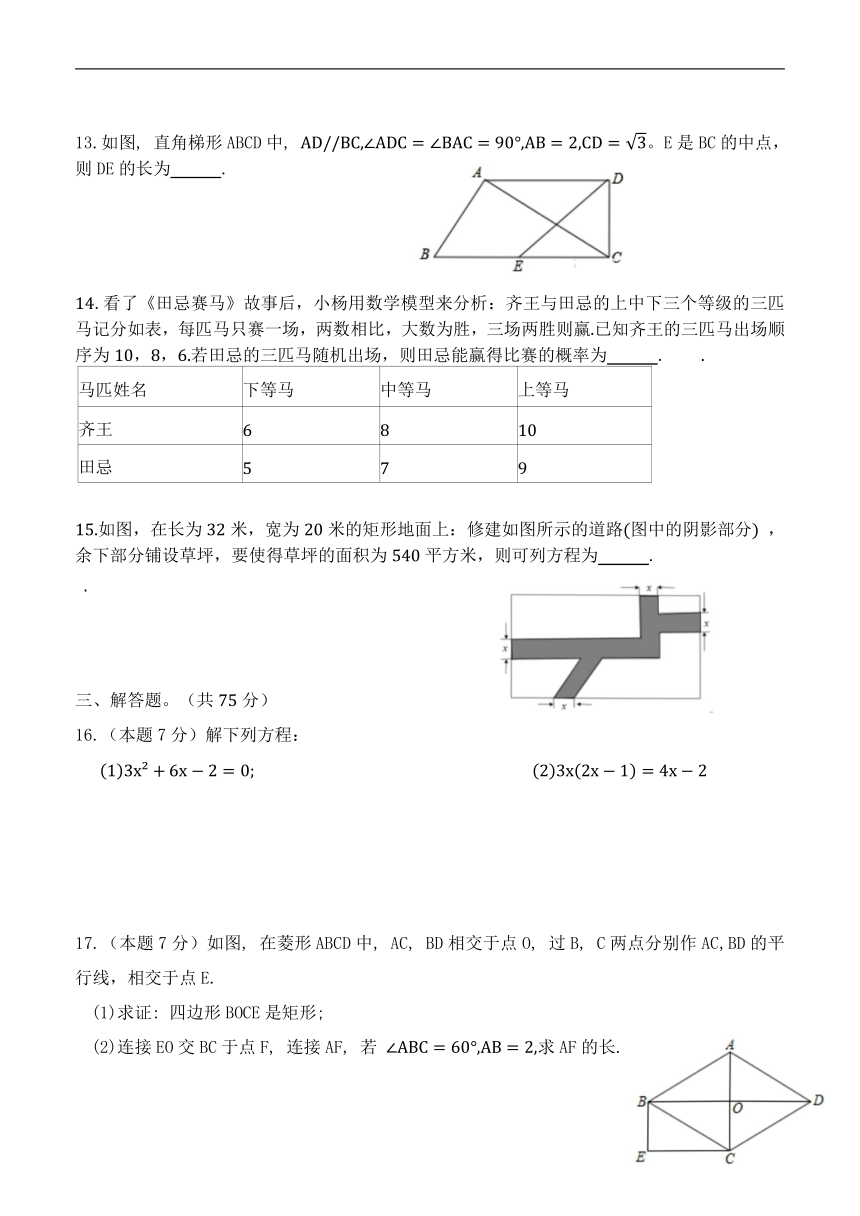
13.如图, 直角梯形ABCD中, E是BC的中点,则DE的长为 .
14.看了《田忌赛马》故事后,小杨用数学模型来分析:齐王与田忌的上中下三个等级的三匹马记分如表,每匹马只赛一场,两数相比,大数为胜,三场两胜则赢.已知齐王的三匹马出场顺序为10,8,6.若田忌的三匹马随机出场,则田忌能赢得比赛的概率为 . .
马匹姓名 下等马 中等马 上等马
齐王 6 8 10
田忌 5 7 9
15.如图,在长为32米,宽为20米的矩形地面上:修建如图所示的道路(图中的阴影部分) ,余下部分铺设草坪,要使得草坪的面积为540平方米,则可列方程为 .
.
三、解答题。(共75分)
16.(本题7分)解下列方程:
17.(本题7分)如图, 在菱形ABCD中, AC, BD相交于点O, 过B, C两点分别作AC,BD的平行线,相交于点E.
(1)求证: 四边形BOCE是矩形;
(2)连接EO交BC于点F, 连接AF, 若 求AF的长.
18.(本题7分)已知关于x的方程x -(k+2)x+2k=0.
(1)求证:无论k取何值,方程总有实数根.
(2)若等腰三角形ABC的一边a=1,另两边长b,c恰好是这个方程的两个根,求△ABC的周长.
19.(本题9分)如图, 中, 于点D, 于点E,( 于点F.
(1) 求证:
(2) 若DE=3, 求CF的长.
20.(本题9分) 为提高学生的综合素养,某校开设了四个兴趣小组,A“健美操”、B“跳绳”、C“剪纸”、D“书法”. 为了了解学生对每个兴趣小组的喜爱情况,随机抽取了部分同学进行调查,并将调查结果绘制出下面不完整的统计图,请结合图中的信息解答下列问题:
(1)本次共调查了 名学生; 并将条形统计图补充完整;
(2)C组所对应的扇形圆心角为 度;
(3)若该校共有学生1400人,则估计该校喜欢跳绳的学生人数约是 ;
(4)现选出了4名跳绳成绩最好的学生,其中有1名男生和3名女生. 要从这4名学生中任意抽取2名学生去参加比赛,请用列表法或画树状图法,求刚好抽到1名男生与1名女生的概率.
21.(本题9分)某商场购进一批台灯,经市场调研:若进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示台灯销售量y(个)与售价x(元)之间的函数关系(
(2)为了让利给顾客,并同时获得840元利润,售价应定为多少
(3)当售价定为多少时,商场获得利润最大,最大利润是多少
22.(本题13分) 【问题发现】我国数学家赵爽在其所著的《勾股圆方图注》中记载了一元二次方程的几何解法.例如x +2x-35=0,可变形为x(x+2)=35.如图1,构造一个长为x+2、宽为x、面积为35的矩形;如图2,将4个矩形构造成一个边长为(x+x+2)的大正方形,中间恰好是一个边长为2的小正方形.大正方形的面积可表示为(x+x+2) ,也可表示为4×35+2 ,由此可得新方程:(x+x+2) =144,易得这个方程的正数解为x=5.
【学以致用】请根据赵爽的方法回答下列问题:
(1)方程x +3x-10=0可变形为x( ______)=10;
(2)能够得出上述方程的解的正确构图是 ______(填序号);
【思维拓展】(3)参照以上方法求出关于x的一元二次方程x +bx=c(b>0,c>0)的正数解(用含b,c的代数式表示).
(本题14分)如图, 在 中, 。动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间t (单位:秒, 。
(1) 当t为何值时,以A,P,M为顶点的三角形与 相似
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值 若存在,求S的最小值; 若不存在,请说明理由.
答案:
一、选择题(共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D D D C D B B D B C
二、解答题。(共15分)
11、1 12、6 13、 14、 15、x -52x+100=0
三、解答题。(共75分)
16、【答案】
则
即
则
∴2x-1=0或3
解得
17、
解: (1) ∵BE∥AC, EC∥BD,
∴四边形BOCE是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD.
∴∠BOC=90°.
∴四边形BOCE是矩形.
∵四边形ABCD是菱形, ∠ABC=60°,
∴△ABC是等边三角形.
∵四边形BOCE是矩形,
∴∠AFB=90°.
∴AF=
18、
解:,
∴不论k何值都有△=(k-2) ≥0,
即方程总有实数根.
当a=1是等腰三角形ABC的底边时, 则有b==c,
方程有相等实数根, 则△=(k-2)=0, 得k=2, 由韦达定理得b+c=k+2=4, 则b=c=2,
∵三边长分别为1,2,2能构成三角形,
∴△ABC的周长是5.
当a=1是等腰三角形ABC的腰时,则方程有一根为x=1, 代入方程得: 1-(k+2)+2k=0, 得k=1,
则解得x =1, x =2,
∵三边长分别为1, 1, 2不能构成三角形,
综上所述, △ABC的周长是5.
19、(1) ∵AB=AC,
∴∠B=∠ACB,
由题意可知: ∠BFC=∠DEC=90°,
∴△BCF∽△CDE;
(2) 设CD=x,
∴BC=2CD=2x,
由 (1) 可知: △BCF∽△CDE,
∴CF=6.
20、(1)40 (2) 72 (3)560人
(4) 画树状图如下:共有12种等可能的结果,其中选出的2名学生恰好为一名男生、一名女生的结果有6种,
∴ 选出的2名学生恰好为一名男生、一名女生的概率为
21、【解答】解:
(1) 设台灯售价为x元时,销售量为y个,
根据题意可知: y=180-10 (x-12) =-10x+300 (12≤x≤30) .
(2) 设获得的利润为W,则
令W=840, 则-10x +400x-3000=840,
解得:
答:为了让利给顾客,并同时获得840元利润,售价应定为16元.
(3) ∵W=-10x +400x-3000=-10 (x-20) +1000,
∵a=-10<0,
∴当x=20时, W取最大值, 最大值为1000.
答:当售价定为20元时,获得利润最大,最大利润是1000元.
22、【解答】解: (1) 方程x +3x-10=0可变形为x (x+3) =10.
故答案为: x+3;
(2) 能够得出上述方程的解的正确构图是②.
故答案为:②;
∴x (x+b) =c,
∴x=
23、解:
∵如图,在Rt△ABC中,∠C =90°,AC=4cm,BC=3cm.
∴根据勾股定理,得
以A, P , M为顶点的三角形与△ABC相似, 分两种情况:
①当△AMP-△ABC时, 即 解得
②当△APM∽△ABC时, 即 解得t=0(不合题意 , 舍去) ;
综上所述,当 时,以A、P、M为顶点的三角形与 相似;
(2)存在某一时刻t,使四边形APNC的面积S有最小值.理由如下:假设存在某一时刻t,使四边形APNC的面积S有最小值.如图,过点P作PH⊥BC于点H.则PH∥AC,
即
∴ S有最小值.
当 时,
答:当 时,四边形APNC的面积. S有最小值,其最小值是
一、选择题(共30分)
1. 关于x的一元二次方程 的一个根为0,则a的值为( )
A.2
B. 0
C.2或-2
D. -2
2. 若关于x的一元二次方程为 的解是x=1, 则2016-a-b的值是( )
A. 2018
B. 2011
C.2014
D.2021
3.某学习小组进行“用频率估计概率”的试验时,统计了某一结果出现的频率如下表,则符合这一结果的试验可能是( )
试验次数 100 200 500 800 1000 1200
试验频率 0.343 0.326 0.335 0.330 0.331 0.330
A.先后两次抛掷一枚质地均匀的硬币,两次都是反面朝上
B.先后两次抛掷一枚质地均匀的骰子,两次的点数和不大于6
C.将一个篮球和一个足球随机放入三个不同的篮子中,恰有一个篮子为空
D.从两男两女四人中抽取两人参加朗读比赛,两人性别相同
4.如果顺次连接四边形的各边中点得到的四边形是正方形,那么原来四边形的对角线一定满足的条件是( )
A.互相平分
B.相等
C.互相垂直
D.互相垂直且相等
5. 若关于x的一元二次方程ax ﹣2x+1=0有实数根,则实数a的取值范围是( )
A. a<1
B. a≤1
C. a≥1
D. a≤1且a≠0
6.等腰三角形三边长分别为a、b、4,且a、b是关于x的一元二次方程x -12x+k+2=0的两根,则k的值为( )
A. 30
B. 34或30
C. 36或30
D. 34
7.如图,在菱形ABCD中,∠D=135°,BE⊥CD于点E,交AC于点F,FG⊥BC于点G.若△BFG的周长为4,则菱形ABCD的面积为( )
A. 4
B. 8
C. 16
D. 16
8. 下列命题正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B. 对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形
D. 一组邻边相等的矩形是正方形
9.为了宣传垃圾分类,童威写了一篇倡议书,决定用微博转发的方式传播. 他设计了如下的传播规则:将倡议书发表在自己的微博上,再邀请n个好友转发,每个好友转发之后,又邀请n个互不相同的好友转发,依次类推. 已知经过两轮转发后,共有111个人参与了宣传活动,则n的值为( )
A.9
B.10
C.11
D.12
10. 如图所示, 在菱形ABCD中, 对角线AC与BD相交于点O, 交BC于点E, 则OE的长为( )
A. 6cm
B.4cm
C.3cm
D. 2cm
二、解答题。(共15分)
11. 已知a, b是 的两个根,则 +b= .
12.如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、AC、BC的中点,点P为线段EF上一个动点, 连接BP、GP, 则 的周长的最小值是 .
13.如图, 直角梯形ABCD中, E是BC的中点,则DE的长为 .
14.看了《田忌赛马》故事后,小杨用数学模型来分析:齐王与田忌的上中下三个等级的三匹马记分如表,每匹马只赛一场,两数相比,大数为胜,三场两胜则赢.已知齐王的三匹马出场顺序为10,8,6.若田忌的三匹马随机出场,则田忌能赢得比赛的概率为 . .
马匹姓名 下等马 中等马 上等马
齐王 6 8 10
田忌 5 7 9
15.如图,在长为32米,宽为20米的矩形地面上:修建如图所示的道路(图中的阴影部分) ,余下部分铺设草坪,要使得草坪的面积为540平方米,则可列方程为 .
.
三、解答题。(共75分)
16.(本题7分)解下列方程:
17.(本题7分)如图, 在菱形ABCD中, AC, BD相交于点O, 过B, C两点分别作AC,BD的平行线,相交于点E.
(1)求证: 四边形BOCE是矩形;
(2)连接EO交BC于点F, 连接AF, 若 求AF的长.
18.(本题7分)已知关于x的方程x -(k+2)x+2k=0.
(1)求证:无论k取何值,方程总有实数根.
(2)若等腰三角形ABC的一边a=1,另两边长b,c恰好是这个方程的两个根,求△ABC的周长.
19.(本题9分)如图, 中, 于点D, 于点E,( 于点F.
(1) 求证:
(2) 若DE=3, 求CF的长.
20.(本题9分) 为提高学生的综合素养,某校开设了四个兴趣小组,A“健美操”、B“跳绳”、C“剪纸”、D“书法”. 为了了解学生对每个兴趣小组的喜爱情况,随机抽取了部分同学进行调查,并将调查结果绘制出下面不完整的统计图,请结合图中的信息解答下列问题:
(1)本次共调查了 名学生; 并将条形统计图补充完整;
(2)C组所对应的扇形圆心角为 度;
(3)若该校共有学生1400人,则估计该校喜欢跳绳的学生人数约是 ;
(4)现选出了4名跳绳成绩最好的学生,其中有1名男生和3名女生. 要从这4名学生中任意抽取2名学生去参加比赛,请用列表法或画树状图法,求刚好抽到1名男生与1名女生的概率.
21.(本题9分)某商场购进一批台灯,经市场调研:若进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示台灯销售量y(个)与售价x(元)之间的函数关系(
(2)为了让利给顾客,并同时获得840元利润,售价应定为多少
(3)当售价定为多少时,商场获得利润最大,最大利润是多少
22.(本题13分) 【问题发现】我国数学家赵爽在其所著的《勾股圆方图注》中记载了一元二次方程的几何解法.例如x +2x-35=0,可变形为x(x+2)=35.如图1,构造一个长为x+2、宽为x、面积为35的矩形;如图2,将4个矩形构造成一个边长为(x+x+2)的大正方形,中间恰好是一个边长为2的小正方形.大正方形的面积可表示为(x+x+2) ,也可表示为4×35+2 ,由此可得新方程:(x+x+2) =144,易得这个方程的正数解为x=5.
【学以致用】请根据赵爽的方法回答下列问题:
(1)方程x +3x-10=0可变形为x( ______)=10;
(2)能够得出上述方程的解的正确构图是 ______(填序号);
【思维拓展】(3)参照以上方法求出关于x的一元二次方程x +bx=c(b>0,c>0)的正数解(用含b,c的代数式表示).
(本题14分)如图, 在 中, 。动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间t (单位:秒, 。
(1) 当t为何值时,以A,P,M为顶点的三角形与 相似
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值 若存在,求S的最小值; 若不存在,请说明理由.
答案:
一、选择题(共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D D D C D B B D B C
二、解答题。(共15分)
11、1 12、6 13、 14、 15、x -52x+100=0
三、解答题。(共75分)
16、【答案】
则
即
则
∴2x-1=0或3
解得
17、
解: (1) ∵BE∥AC, EC∥BD,
∴四边形BOCE是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD.
∴∠BOC=90°.
∴四边形BOCE是矩形.
∵四边形ABCD是菱形, ∠ABC=60°,
∴△ABC是等边三角形.
∵四边形BOCE是矩形,
∴∠AFB=90°.
∴AF=
18、
解:,
∴不论k何值都有△=(k-2) ≥0,
即方程总有实数根.
当a=1是等腰三角形ABC的底边时, 则有b==c,
方程有相等实数根, 则△=(k-2)=0, 得k=2, 由韦达定理得b+c=k+2=4, 则b=c=2,
∵三边长分别为1,2,2能构成三角形,
∴△ABC的周长是5.
当a=1是等腰三角形ABC的腰时,则方程有一根为x=1, 代入方程得: 1-(k+2)+2k=0, 得k=1,
则解得x =1, x =2,
∵三边长分别为1, 1, 2不能构成三角形,
综上所述, △ABC的周长是5.
19、(1) ∵AB=AC,
∴∠B=∠ACB,
由题意可知: ∠BFC=∠DEC=90°,
∴△BCF∽△CDE;
(2) 设CD=x,
∴BC=2CD=2x,
由 (1) 可知: △BCF∽△CDE,
∴CF=6.
20、(1)40 (2) 72 (3)560人
(4) 画树状图如下:共有12种等可能的结果,其中选出的2名学生恰好为一名男生、一名女生的结果有6种,
∴ 选出的2名学生恰好为一名男生、一名女生的概率为
21、【解答】解:
(1) 设台灯售价为x元时,销售量为y个,
根据题意可知: y=180-10 (x-12) =-10x+300 (12≤x≤30) .
(2) 设获得的利润为W,则
令W=840, 则-10x +400x-3000=840,
解得:
答:为了让利给顾客,并同时获得840元利润,售价应定为16元.
(3) ∵W=-10x +400x-3000=-10 (x-20) +1000,
∵a=-10<0,
∴当x=20时, W取最大值, 最大值为1000.
答:当售价定为20元时,获得利润最大,最大利润是1000元.
22、【解答】解: (1) 方程x +3x-10=0可变形为x (x+3) =10.
故答案为: x+3;
(2) 能够得出上述方程的解的正确构图是②.
故答案为:②;
∴x (x+b) =c,
∴x=
23、解:
∵如图,在Rt△ABC中,∠C =90°,AC=4cm,BC=3cm.
∴根据勾股定理,得
以A, P , M为顶点的三角形与△ABC相似, 分两种情况:
①当△AMP-△ABC时, 即 解得
②当△APM∽△ABC时, 即 解得t=0(不合题意 , 舍去) ;
综上所述,当 时,以A、P、M为顶点的三角形与 相似;
(2)存在某一时刻t,使四边形APNC的面积S有最小值.理由如下:假设存在某一时刻t,使四边形APNC的面积S有最小值.如图,过点P作PH⊥BC于点H.则PH∥AC,
即
∴ S有最小值.
当 时,
答:当 时,四边形APNC的面积. S有最小值,其最小值是
同课章节目录
