7.5 正态分布 同步练习(含解析) 高二数学人教A版(2019)选择性必修三
文档属性
| 名称 | 7.5 正态分布 同步练习(含解析) 高二数学人教A版(2019)选择性必修三 |

|
|
| 格式 | docx | ||
| 文件大小 | 225.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-15 18:50:58 | ||
图片预览


文档简介
7.5 正态分布
教材课后习题
1.对某地区数学考试成绩的数据分析,男生成绩X服从正态分布,女生成绩Y服从正态分布.请你从不同角度比较男、女生的考试成绩.
2.某市高二年级男生的身高X(单位:)近似服从正态分布随机选择一名本市高二年级的男生,求下列事件的概率:
(1);
(2);
(3).
3.若,则X位于区域内的概率是多少?
4.袋装食盐标准质量为,规定误差的绝对值不超过就认为合格.假设误差服从正态分布,随机抽取100袋食盐,误差的样本均值为0,样本方差为4.请你估计这批袋装食盐的合格率.
定点变式训练
5.已知随机变量,,则的值为( )
A.0.24 B.0.26 C.0.68 D.0.76
6.设随机变量服从正态分布.若,则a的值为( )
A. B.1 C.2 D.
7.已知随机变量X服从正态分布,且,则( )
A.0.1 B.0.2 C.0.3 D.0.4
8.已知随机变量,则( )
参考数据:若,,,.
A.0.0148 B.0.1355 C.0.1574 D.0.3148
9.(多选)已知随机变量X服从正态分布,则下列说法正确的有( )
A. B. C. D.
10.已知随机变量X服从正态分布,若,则__________.
11.某学校组织1200名学生进行“防疫知识测试”,测试后统计分析如下:学生的平均成绩为,方差为.学校要对成绩不低于90分的学生进行表彰,假设学生的测试成绩X近似服从正态分布(其中近似为平均数,近似为方差),则估计获表彰的学生人数为__________(四舍五入,保留整数).
参考数据:若随机变量X服从正态分布,则,,.
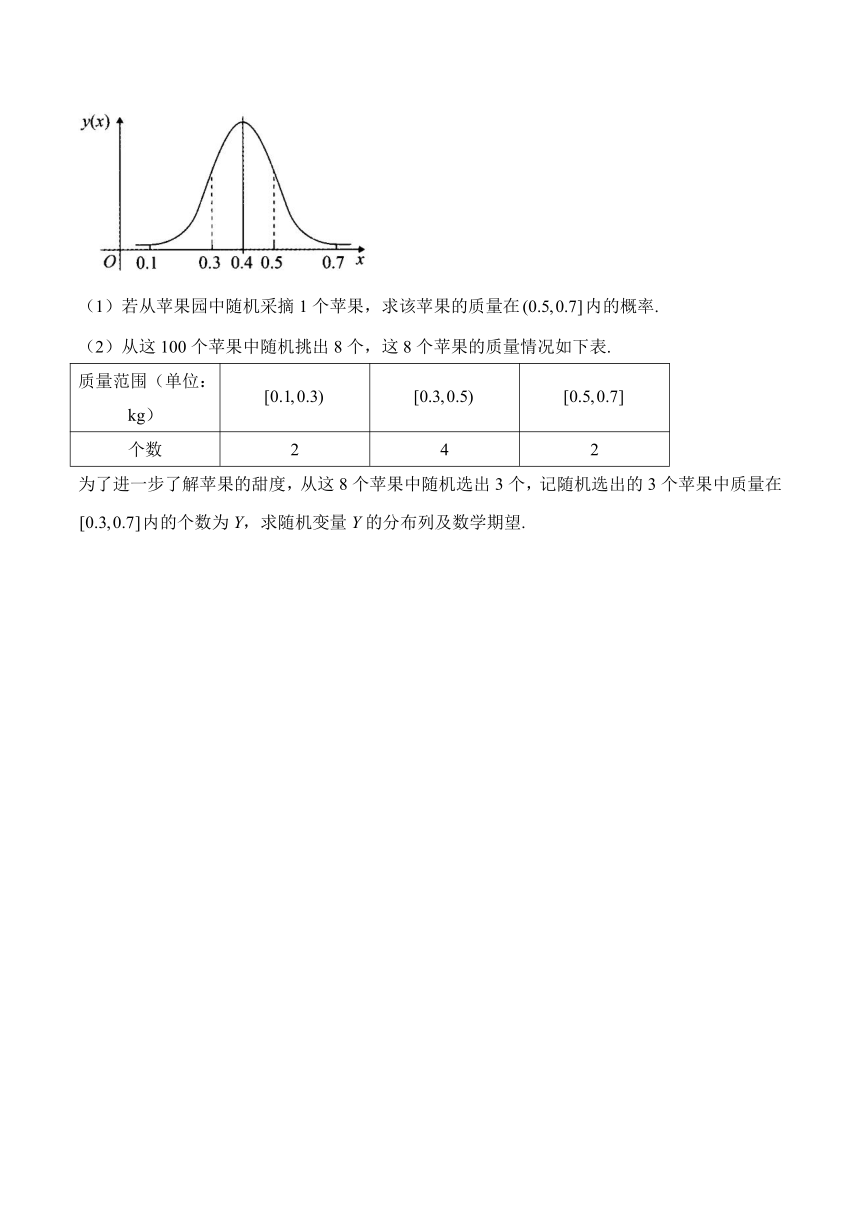
12.为了调查某苹果园中苹果的生长情况,在苹果园中随机采摘了100个苹果.经整理分析后发现,苹果的质量X(单位:kg)近似服从正态分布,其正态分布密度曲线如图,已知,.
(1)若从苹果园中随机采摘1个苹果,求该苹果的质量在内的概率.
(2)从这100个苹果中随机挑出8个,这8个苹果的质量情况如下表.
质量范围(单位:kg)
个数 2 4 2
为了进一步了解苹果的甜度,从这8个苹果中随机选出3个,记随机选出的3个苹果中质量在内的个数为Y,求随机变量Y的分布列及数学期望.
答案以及解析
1.答案:从均值看,说明女生的平均成绩较好;
从方差看,说明女生成绩更稳定
解析:男生成绩X服从正态分布,
,.
女生成绩Y服从正态分布,
,.
从均值看,说明女生的平均成绩较好;
从方差看,说明女生成绩更稳定.
2.答案:(1)
(2)
(3)
解析:,,.
(1).
(2)
.
(3).
3.答案:
解析:,.
4.答案:
解析:设误差为X,由题意,
,,
.
5.答案:A
解析:因为随机变量,,所以.由正态曲线的对称性得,.故选A.
6.答案:B
解析:随机变量服从正态分布,根据正态曲线的对称性,可得,解得.故选B.
7.答案:C
解析:.
8.答案:B
解析:因为,即,,所以,.
又,,且,故选B.
9.答案:BC
解析:随机变量X服从正态分布,则,,,.故选BC.
10.答案:
解析:,,又,,.
11.答案:27
解析:由题意得,,,则,所以,所以.
12.答案:(1)0.2
(2)Y的分布列见解析;数学期望为
解析:(1)已知苹果的质量X(单位:kg)近似服从正态分布,
则由正态曲线的对称性可知,
,
所以从苹果园中随机采摘1个苹果,该苹果的质量在内的概率为0.2.
(2)由题意可知,随机变量Y的所有可能取值为1,2,3,
则,,,
所以随机变量Y的分布列为
Y 1 2 3
P
所以.
教材课后习题
1.对某地区数学考试成绩的数据分析,男生成绩X服从正态分布,女生成绩Y服从正态分布.请你从不同角度比较男、女生的考试成绩.
2.某市高二年级男生的身高X(单位:)近似服从正态分布随机选择一名本市高二年级的男生,求下列事件的概率:
(1);
(2);
(3).
3.若,则X位于区域内的概率是多少?
4.袋装食盐标准质量为,规定误差的绝对值不超过就认为合格.假设误差服从正态分布,随机抽取100袋食盐,误差的样本均值为0,样本方差为4.请你估计这批袋装食盐的合格率.
定点变式训练
5.已知随机变量,,则的值为( )
A.0.24 B.0.26 C.0.68 D.0.76
6.设随机变量服从正态分布.若,则a的值为( )
A. B.1 C.2 D.
7.已知随机变量X服从正态分布,且,则( )
A.0.1 B.0.2 C.0.3 D.0.4
8.已知随机变量,则( )
参考数据:若,,,.
A.0.0148 B.0.1355 C.0.1574 D.0.3148
9.(多选)已知随机变量X服从正态分布,则下列说法正确的有( )
A. B. C. D.
10.已知随机变量X服从正态分布,若,则__________.
11.某学校组织1200名学生进行“防疫知识测试”,测试后统计分析如下:学生的平均成绩为,方差为.学校要对成绩不低于90分的学生进行表彰,假设学生的测试成绩X近似服从正态分布(其中近似为平均数,近似为方差),则估计获表彰的学生人数为__________(四舍五入,保留整数).
参考数据:若随机变量X服从正态分布,则,,.
12.为了调查某苹果园中苹果的生长情况,在苹果园中随机采摘了100个苹果.经整理分析后发现,苹果的质量X(单位:kg)近似服从正态分布,其正态分布密度曲线如图,已知,.
(1)若从苹果园中随机采摘1个苹果,求该苹果的质量在内的概率.
(2)从这100个苹果中随机挑出8个,这8个苹果的质量情况如下表.
质量范围(单位:kg)
个数 2 4 2
为了进一步了解苹果的甜度,从这8个苹果中随机选出3个,记随机选出的3个苹果中质量在内的个数为Y,求随机变量Y的分布列及数学期望.
答案以及解析
1.答案:从均值看,说明女生的平均成绩较好;
从方差看,说明女生成绩更稳定
解析:男生成绩X服从正态分布,
,.
女生成绩Y服从正态分布,
,.
从均值看,说明女生的平均成绩较好;
从方差看,说明女生成绩更稳定.
2.答案:(1)
(2)
(3)
解析:,,.
(1).
(2)
.
(3).
3.答案:
解析:,.
4.答案:
解析:设误差为X,由题意,
,,
.
5.答案:A
解析:因为随机变量,,所以.由正态曲线的对称性得,.故选A.
6.答案:B
解析:随机变量服从正态分布,根据正态曲线的对称性,可得,解得.故选B.
7.答案:C
解析:.
8.答案:B
解析:因为,即,,所以,.
又,,且,故选B.
9.答案:BC
解析:随机变量X服从正态分布,则,,,.故选BC.
10.答案:
解析:,,又,,.
11.答案:27
解析:由题意得,,,则,所以,所以.
12.答案:(1)0.2
(2)Y的分布列见解析;数学期望为
解析:(1)已知苹果的质量X(单位:kg)近似服从正态分布,
则由正态曲线的对称性可知,
,
所以从苹果园中随机采摘1个苹果,该苹果的质量在内的概率为0.2.
(2)由题意可知,随机变量Y的所有可能取值为1,2,3,
则,,,
所以随机变量Y的分布列为
Y 1 2 3
P
所以.
