北京市第五中学2024-2025学年高三(上)期中考试数学试卷(PDF版,含答案)
文档属性
| 名称 | 北京市第五中学2024-2025学年高三(上)期中考试数学试卷(PDF版,含答案) |

|
|
| 格式 | |||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-16 21:40:42 | ||
图片预览




文档简介
2024/2025学年度第一学期期中检测试卷
高三数学
班级______ 姓名_______学号______ 成绩________
一. 选择题(共 10小题,每小题 4分,共 40分.在每小题列出的四个选项中,选出符合题目要求
的
一项)
(1)已知集合 A 1,0,1 ,若 A B 1,0,1,2,3 ,则集合 B可以是
(A) (B) 1,0,1
(C) 2,3,4 (D) 1,2,3
(2)若直线 ax y a 1 0与直线 x ay 3a 3 0平行,则实数的 a值为
(A) 0 (B) 1
(C)1 (D) 1或1
2
(3) y曲线C是双曲线,则“C的方程是 x2 1”是“C的渐近线方程为 y 2x ”的
4
(A)充分不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(4)已知函数 f (x) sin x 3 cos x ,设 a f ( ),b f ( ),c f ( ),则 a, b, c的大小关
7 6 3
系是
(A)a b c (B)b a c
(C)c a b (D)b c a
(5)已知两点 A( 2,0), B(0, 2),点C是圆 x2 y2 4x 4y 6 0上任意一点,则VABC面
积的最小值是
(A)8 (B)6
(C)3 2 (D)4
(6)已知抛物线C: y2=12x的焦点为 F,准线为 l,点 A在C上,过 A点作准线 l的垂线交准线
2π
于B,若 FAB ,则 BF
3
(A) 2 3 (B) 4 3
(C) 4 3 (D) 8 3
3 3
1
(7)中国古代数学的瑰宝《九章算术》中记载了一种称为“曲池”的几何体,该
几何体为上、下底面均为扇环形的柱体(扇环是指圆环被扇形截得的部分).现
有一个如下图所示的“曲池”,其高为3, AA1 底面,底面扇环所对的圆心角
为 , AD长度为 B C长度的 3倍,且线段 AB CD 2,则该“曲池”的体积为2
9
(A) (B)5
2
11
(C) (D)6
2
(8)在直角三角形VABC中, A 90 , AB 2, AC 4,点 P在VABC斜边 BC的中线 AD上,
uur uuur
则 PB PC的取值范围
(A)[ 5,0] (B)[ 3,0]
(C)[0,3] (D)[0,5]
(9)金针菇采摘后会很快失去新鲜度,甚至腐烂,所以超市销售金针菇时需要采取保鲜膜封闭保
存.已知金针菇失去的新鲜度h与其采摘后时间 t(天)满足的函数解析式为 h mln t a a 0 .
若采摘后1天,金针菇失去的新鲜度为 40%;若采摘后3天,金针菇失去的新鲜度为80%.现在
金针菇失去的新鲜度为60%,则采摘后的天数为(结果保留一位小数, 2 1.41)
(A)1.5 (B)1.8
(C) 2.0 (D) 2.1
(10)已知定点 A(3,0), B(0,4),若点C在圆O : x2 y2 4上运动,则2 CA CB 的最小值为
(A)2 10 (B)6
(C) 2 + 2 5 (D)2 + 2 13
二.填空题(共 5小题,每小题 5分,共 25分)
2
(11)复数 z 的共轭复数 z .
1 i
(12)已知 ABCD为正方形,若椭圆M 与双曲线N 都以 A B 为焦点,且图像都过C D点,则椭
圆M 的离心率为 ,双曲线 N的离心率为 .
2
(13)在 ABC 中, AB 4 3 , B ,点 D 在边 BC 上, ADC , CD 2 ,则4 3
AD ; ACD的面积为 .
2
(14)已知函数 f x e x t , g x x e, h x max f x , g x ,其中max a,b 表
示a,b中最大的数.若 t 1,则 h 0 ________;若 h x e对 x R恒成立,则 t的取值范
围是________.
(15)已知函数 f (x) 2x3 3x.给出下列四个结论:
①过点 A(0, 2)存在 1 条直线与曲线 y f (x)相切;
②过点 B(2,10)存在 2 条直线与曲线 y f (x)相切;
③过点C( 1,2)存在 3 条直线与曲线 y f (x)相切;
④过点D(1, t)存在 3条直线与曲线 y f (x)相切时, t的取值范围是 ( 3, 2).
其中,正确结论的序号是________.
三.解答题(共 6小题,共 85分)
(16)(本小题 14分)
如图,在直三棱柱 ABC A1B1C1中,AA1 AC 4,AB 3,
BC 5,点D是线段 BC的中点.
(Ⅰ)求证: AB A1C;
(Ⅱ)试求二面角D CA1 A的余弦值;
(III)求点B1到平面 A1CD的距离.
3
(17) (本小题 13分)
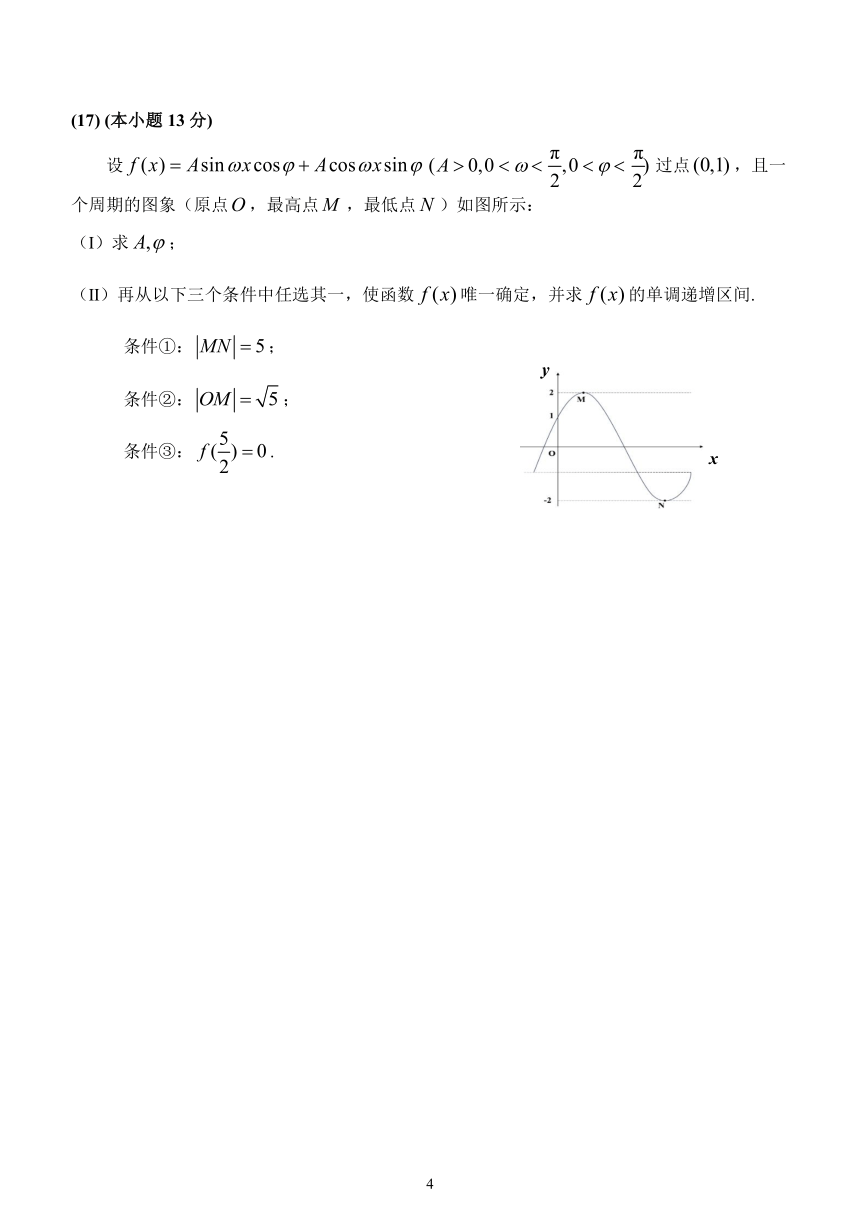
设 f (x) Asin xcos Acos xsin (A 0,0 π ,0 π ) 过点 (0,1),且一
2 2
个周期的图象(原点O,最高点M ,最低点 N )如图所示:
(Ⅰ)求 A, ;
(Ⅱ)再从以下三个条件中任选其一,使函数 f (x)唯一确定,并求 f (x)的单调递增区间.
条件①: MN 5;
y
条件②: OM 5;
5
条件③: f ( ) 0 .
2 x
4
(18) (本小题 13分)
自 2022北京冬奥会以来,花样滑冰项目引起了广泛关注.选手们在冰上起舞,做出步法、
旋转、跳跃等技术动作.“技术动作分”由“基础分”和“执行分”相加得到.不同的技术动作,其“基
础分”也不同,其中四个跳跃动作 4T,4S,4F,4Lz的“基础分”如表 1所示.
跳跃动作 4T 4S 4F 4Lz
基础分 9.5 9.7 11.0 11.5
表 1
选手表演完,得到相应动作的“执行分”.把“执行分”为非负值的跳跃动作记为“成功”,否则
记为“失败”.表 2为某选手在上一赛季各跳跃动作的“技术动作分”.
4T 12.04 11.22 4.75 9.06 9.97 11.63 10.98
4S 10.98 10.57 11.32 4.85 9.51 12.07
4F 13.69 5.50 14.02 12.92
4Lz 13.54 14.23 11.21 8.38 11.87
表 2
假设用频率估计概率,且选手每个跳跃动作是否“成功”相互独立.
(Ⅰ)从该选手上一赛季所有 4T动作中任选一次,估计这次跳跃为“成功”的概率;
(Ⅱ)若该选手在本赛季中,计划完成 4T,4S,4F 这三个动作,且每个动作只完成一次.将这
三个动作中成功的跳跃个数记为 X,求 X的分布列和数学期望 E(X);
(III)在本赛季中,从四个跳跃动作 4T,4S,4F,4Lz中选出三个,使得该选手这三个动作中
“成功”的跳跃个数的期望最大,请直接写出这三个动作的名称.
5
(19) (本小题 15分)
已知函数 ( ) = ,其中 > 0.
(I)当 = 2 时,求曲线 = ( )在点(2, (2))处的切线方程;
(Ⅱ)求 y f ( x )的单调区间;
(III)当 1 < 2且 1 2 > 0时,判断 ( 1) (
1 1
2)与 的大小,并说明理由.1 2
(20) (本小题 15分)
x2 y2 3
设椭圆M : 1(a b 0),且离心率为 ,过点 P(4,0)的直线与椭圆交于 A,B
a2 b2 2
两点,当直线 AB经过椭圆中心O时, AB 4 .
(Ⅰ)求椭圆M 的方程;
(Ⅱ)已知点T (1,1),直线 AT 和直线 BT 分别与 y 轴交于C, D ,与 x 轴交于 E , F ,若
3S CDT S EFT ,求直线 AB的斜率.
(21) (本小题 15分)
an
{a } ,an为偶数,设正整数数列 n 满足 an 1 2 n 1,2,...... .
an+5,an为奇数.
(1)若 a6 1,请写出 a1所有可能的取值;
(2)记集合M a *n | n N ,且 a1不是 5的倍数,求证:1 M ;
*
(3)存在常数T,对于 n N 都有 an T an,求 a1所有可能的取值.
6
答案
一.选择题
1 2 3 4 5 6 7 8 9 10
D B A C D B D A B A
二.填空题
11. 1 i
12. 2 1, 2 1
13. 4 2,2 6
14. e, , 1 .
15. ①②③
三.解答题
16.【答案】解:(1)证明:在△ 中,∵ = 4, = 3, = 5,
∴ 2 + 2 = 2,∴ ⊥ ,
∵ 1 ⊥平面 , 平面 ,
∴ 1 ⊥ ,
又 ∩ 1 = , , 1 平面 1 ,
∴ ⊥平面 1 ,又 1 平面 1 ,
∴ ⊥ 1C. 5分
(2)由(1)可知, 1 ⊥平面 , , 平面 ,所以 1 ⊥ , 1 ⊥ ,
又 ⊥ ,
以 为原点,以 , , 1为坐标轴建立空间直角坐标系 ,如图所示,
则 (0,0,0), (0,3,0), (4,0,0), 1(0,0,4), (2,
3
2 , 0),
∴ ��� �� = (0,3,0), ��� ��1� = ( 4,0,4),� �� �� = ( 2,
3
2 , 0),
7
∵ ⊥平面 1 ,∴ � �� ��是平面 1 的一个法向量,
设平面 1的法向量为� � = ( , , ),
� � ��� ��1� = 0 4 + 4 = 0则 ,即 3 ,解得 =
4
2 + = 0 3 ,� � ��� �� = 0 2 =
令 = 1 4可得� � = (1, 3 , 1),
�����
∴ cos < � �, ��� �� >= � � = 4 2 34
| ��|| ��� ��| 34
=
×3 17
,
3
由图形可知二面角 1 为锐二面角,
∴二面角 1 的余弦值为
2 34. 11分
17
(3)由(2)可知,� ��1� ���1� = ��� �� = (0,3,0),
设 1 1与平面 1 所成角为 ,
则 = |cos < � ��1� ���1�,� � > | =
2 34,
17
∴ 1到平面 1 的距离为|� ��1� ���1�| = 3 ×
2 34 = 6 34. 14分17 17
(17)解:(Ⅰ) f (x) Asin( x )过 (0,1)
结合图象,有:1 2sin
则由0 π π ,有
2 6
π
所以 A 2, 【5分】
6
(Ⅱ)选择条件①
MN 5 xM xN 3
T π
则 3 π
2 3
f (x) π π故 2sin( x )
3 6
π 2kπ π x π π令 2kπ,
2 3 6 2
有 2 6k x 1 6k ,
所以 f (x)单调递增区间为[ 2 6k ,1 6k ], k Z 【13分】
8
选择条件②
OM 5 xM 1 M (1,2)
则 2 2sin( π )
6
π π
由0 ,有
2 3
f (x) π π故 2sin( x )
3 6
以下同①
选择条件③
f (5) 0 sin(5 π) 0 2kπ π (k Z ),
2 2 6 5 15
由0 π π ,有
2 3
故 f (x) 2sin( π x π )
3 6
以下同①
5
(18)(1)
7
179
(2)分布列见解析,数学期望为
84
(3)4T,4S, 4F
【分析】(1)根据题意,结合表格的数据,结合古典概型的概率公式代入计算,即可得到结果;
(2)根据题意,由条件可得 X的所有可能取值为 0,1,2,3,然后分别计算对应的概率,即可得
到分布列,再由期望的计算公式即可得到结果.
(3)根据题意,结合表格中的数据即可得到结果.
【详解】(1)根据题中数据,该选手上一赛季 7个 4T动作中,有 5个跳跃为“成功”,所以从该
5
选手上一赛季所有 4T动作中任选一次,这次跳跃“成功”的概率可以估计为 . 4分
7
(2)同(1),从该选手上一赛季所有 4S,4F动作中分别任选一次,这次跳跃“成功”的概率分
2
别可以估计为 ,
3
,
3 4
X的所有可能取值为 0,1,2,3.
P X 0 1 5 1 2 3 1
1 ,
7 3 4 42
9
P X 1 5 2 3 5 1 1 1 2 1 3 1 5 1 2 3 5
7 3
,
4 7 3 4 7 3 4 28
P X 2 5 2 3 5 2 3 5 2 3 37 5 2 3 5
7 3
1 1 1 , P X 3 .
4 7 3 4 7 3 4 84 7 3 4 14
所以随机变量 X的分布列为:
X 0 1 2 3
1 5 37 5
P
42 28 84 14
所以 E X 0 1 5 37 1 2 3 5 179 . 10分
42 28 84 14 84
5 2
(3)由表格可知,4T动作成功的概率为 ,失败的概率为 ,
7 7
2 1
4S动作成功的概率为 ,失败的概率为 ,
3 3
3
4F 1动作成功的概率为 ,失败的概率为 ,
4 4
3 2
4Lz动作成功的概率为 ,失败的概率为 ,
5 5
3 5 2 3
由 可知,选 4T,4S, 4F. 13分
4 7 3 5
2 2
(19)解:(1)当 = 2 时, ( ) = ; '( ) = (2 1)
2
;
4 4
而 (2) = , '(2) = 3 ;
2 4
4 3 4 3 4
故曲线 = ( )在点(2, (2))处的切线方程为 = ( 2),即 = 4. 4分
2 4 4
' ( 1) (2) ( )的定义域为( ∞,0) ∪ (0, + ∞),且 ( ) = ;令 '2 ( ) = 0,
1
得 = .
当 变化时, '( )与 ( )的变化情况如下表:
( ∞,0) 1 1 1(0, ) ( , + ∞)
'( ) 0 +
( ) 单调递减 单调递减 极小值 单调递增
所以 ( ) ( 1的单调递增区间为 , + ∞);单调递减区间为( ∞,0) 1和(0, ); 9分
(3)当 < 且 > 0 1 1时, 1 2 < ,证明如下: 1 2
10
= 1 , ' = 1
+1
令 则
2
.
设 = 1 + 1,则 ' = .
所以当 x∈(--∞,0)时, ' < 0;当 ∈ 0 +∞ 时, ' > 0.
所以 h(x)在(--∞,0)上单调递减,在( 0 +∞ 上单调递增.
从而 h(x)>h(0)=0,即 ' > 0,
所以 g(x)的单调递增区间为(--∞,0)和( 0 +∞ .
当 0 < < 时, < ,即 1 <
1 12 ; 1 2
当 1 <
1 1
2 < 0 时, < ,即 1 2 < . 1 2
综上,当 1 < 2且 1 2 > 0时, ( 1) ( ) <
1 1
2 . 15分 1 2
2a 4 a 2 x2
(20)解:(Ⅰ ) 1 ,所以M : y2 1; 5分
2a 2b 4 b 1 4 2
(Ⅱ)①当直线 AB的方程为 = 0时,显然 A( 2,0), B(2,0);
直线 AT 的方程为 = + 2, 2所以 C(0, );
3 3 3
直线 BT的方程为 = + 2,所以 D(0,2);
此时点 E与点 A重合,点 F与点 B重合,易知3S CDT S EFT ;
②设直线 AB : x my 4, A(x1, y1),B(x2, y2)
x2 4y2 4
(m2 4)y2 8my 12 0,
x my 4
64m2 48(m2 4) 0 m2,即 12 0,也即m 2 3或m 2 3 3 3,k ( , );
6 6
y 8m 121 y2 2 , y1y ;m 4 2 m2 4
x x 32
2
1 2 2 , x1x
4m 64
2 ;m 4 m2 4
3S CDT S EFT 3CD EF 3 yC yD xE xF
11
直线 AT : y 1 y1 1 y 1 (x 1),直线 BT : y 1 2 (x 1)
x1 1 x2 1
令 x 0,C(0, y 1 1 1),D(0, y 2 1 1)
x1 1 x2 1
y 0 E( x1 1令 , 1,0) x 1, F ( 2 1,0)
y1 1 y2 1
3 y1 1 y则 2 1 x1 1 x 1 2
x1 1 x2 1 y1 1 y2 1
即 x1x2 (x1 x2 ) 1 3 y1y2 (y1 y2 ) 1
也即 4m2 64 32 m2 4 3 12 8m m2 4
3m2 36 3 m2 8m 16
则 24m 84 0 7,m 2 3 3,斜率为 ( , );
2 7 6 6
综上,直线 AB的斜率为 0或 2 . 15分
7
(21)(1)a1 6,a1 11,a1 32 4分
(2)设 t中最小数为ak t, t,k N
*
t
①当 t为偶数时, ak 1 t与 t是最小值矛盾2
t 5
②当 t为奇数时,ak 1 t 5是偶数, ak 2 t2
t 5
t 1或3或5.
1)当 t 5时, ak 1也是5的倍数,以此类推…, a1也是5的倍数,与 a1不是 5的倍数
矛盾.
2)当 t 3时,ak 1 8,ak 2 4,ak 3 2,ak 4 1 t,矛盾,
t 1,即1 M成立. 9分
(3)由第(2)问可知, an 中最小数只能是1或 5.
12
当 t 1时,后面的项为6,3,8,4,2,1……
当 t 5时,后面的项为10,5,10,5……
所以数列 an 为周期数列时,只能是1,2,3,4,5,6,8,10
所以a1 {1,2,3,4,5,6,8,10} 15分
13
14
高三数学
班级______ 姓名_______学号______ 成绩________
一. 选择题(共 10小题,每小题 4分,共 40分.在每小题列出的四个选项中,选出符合题目要求
的
一项)
(1)已知集合 A 1,0,1 ,若 A B 1,0,1,2,3 ,则集合 B可以是
(A) (B) 1,0,1
(C) 2,3,4 (D) 1,2,3
(2)若直线 ax y a 1 0与直线 x ay 3a 3 0平行,则实数的 a值为
(A) 0 (B) 1
(C)1 (D) 1或1
2
(3) y曲线C是双曲线,则“C的方程是 x2 1”是“C的渐近线方程为 y 2x ”的
4
(A)充分不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(4)已知函数 f (x) sin x 3 cos x ,设 a f ( ),b f ( ),c f ( ),则 a, b, c的大小关
7 6 3
系是
(A)a b c (B)b a c
(C)c a b (D)b c a
(5)已知两点 A( 2,0), B(0, 2),点C是圆 x2 y2 4x 4y 6 0上任意一点,则VABC面
积的最小值是
(A)8 (B)6
(C)3 2 (D)4
(6)已知抛物线C: y2=12x的焦点为 F,准线为 l,点 A在C上,过 A点作准线 l的垂线交准线
2π
于B,若 FAB ,则 BF
3
(A) 2 3 (B) 4 3
(C) 4 3 (D) 8 3
3 3
1
(7)中国古代数学的瑰宝《九章算术》中记载了一种称为“曲池”的几何体,该
几何体为上、下底面均为扇环形的柱体(扇环是指圆环被扇形截得的部分).现
有一个如下图所示的“曲池”,其高为3, AA1 底面,底面扇环所对的圆心角
为 , AD长度为 B C长度的 3倍,且线段 AB CD 2,则该“曲池”的体积为2
9
(A) (B)5
2
11
(C) (D)6
2
(8)在直角三角形VABC中, A 90 , AB 2, AC 4,点 P在VABC斜边 BC的中线 AD上,
uur uuur
则 PB PC的取值范围
(A)[ 5,0] (B)[ 3,0]
(C)[0,3] (D)[0,5]
(9)金针菇采摘后会很快失去新鲜度,甚至腐烂,所以超市销售金针菇时需要采取保鲜膜封闭保
存.已知金针菇失去的新鲜度h与其采摘后时间 t(天)满足的函数解析式为 h mln t a a 0 .
若采摘后1天,金针菇失去的新鲜度为 40%;若采摘后3天,金针菇失去的新鲜度为80%.现在
金针菇失去的新鲜度为60%,则采摘后的天数为(结果保留一位小数, 2 1.41)
(A)1.5 (B)1.8
(C) 2.0 (D) 2.1
(10)已知定点 A(3,0), B(0,4),若点C在圆O : x2 y2 4上运动,则2 CA CB 的最小值为
(A)2 10 (B)6
(C) 2 + 2 5 (D)2 + 2 13
二.填空题(共 5小题,每小题 5分,共 25分)
2
(11)复数 z 的共轭复数 z .
1 i
(12)已知 ABCD为正方形,若椭圆M 与双曲线N 都以 A B 为焦点,且图像都过C D点,则椭
圆M 的离心率为 ,双曲线 N的离心率为 .
2
(13)在 ABC 中, AB 4 3 , B ,点 D 在边 BC 上, ADC , CD 2 ,则4 3
AD ; ACD的面积为 .
2
(14)已知函数 f x e x t , g x x e, h x max f x , g x ,其中max a,b 表
示a,b中最大的数.若 t 1,则 h 0 ________;若 h x e对 x R恒成立,则 t的取值范
围是________.
(15)已知函数 f (x) 2x3 3x.给出下列四个结论:
①过点 A(0, 2)存在 1 条直线与曲线 y f (x)相切;
②过点 B(2,10)存在 2 条直线与曲线 y f (x)相切;
③过点C( 1,2)存在 3 条直线与曲线 y f (x)相切;
④过点D(1, t)存在 3条直线与曲线 y f (x)相切时, t的取值范围是 ( 3, 2).
其中,正确结论的序号是________.
三.解答题(共 6小题,共 85分)
(16)(本小题 14分)
如图,在直三棱柱 ABC A1B1C1中,AA1 AC 4,AB 3,
BC 5,点D是线段 BC的中点.
(Ⅰ)求证: AB A1C;
(Ⅱ)试求二面角D CA1 A的余弦值;
(III)求点B1到平面 A1CD的距离.
3
(17) (本小题 13分)
设 f (x) Asin xcos Acos xsin (A 0,0 π ,0 π ) 过点 (0,1),且一
2 2
个周期的图象(原点O,最高点M ,最低点 N )如图所示:
(Ⅰ)求 A, ;
(Ⅱ)再从以下三个条件中任选其一,使函数 f (x)唯一确定,并求 f (x)的单调递增区间.
条件①: MN 5;
y
条件②: OM 5;
5
条件③: f ( ) 0 .
2 x
4
(18) (本小题 13分)
自 2022北京冬奥会以来,花样滑冰项目引起了广泛关注.选手们在冰上起舞,做出步法、
旋转、跳跃等技术动作.“技术动作分”由“基础分”和“执行分”相加得到.不同的技术动作,其“基
础分”也不同,其中四个跳跃动作 4T,4S,4F,4Lz的“基础分”如表 1所示.
跳跃动作 4T 4S 4F 4Lz
基础分 9.5 9.7 11.0 11.5
表 1
选手表演完,得到相应动作的“执行分”.把“执行分”为非负值的跳跃动作记为“成功”,否则
记为“失败”.表 2为某选手在上一赛季各跳跃动作的“技术动作分”.
4T 12.04 11.22 4.75 9.06 9.97 11.63 10.98
4S 10.98 10.57 11.32 4.85 9.51 12.07
4F 13.69 5.50 14.02 12.92
4Lz 13.54 14.23 11.21 8.38 11.87
表 2
假设用频率估计概率,且选手每个跳跃动作是否“成功”相互独立.
(Ⅰ)从该选手上一赛季所有 4T动作中任选一次,估计这次跳跃为“成功”的概率;
(Ⅱ)若该选手在本赛季中,计划完成 4T,4S,4F 这三个动作,且每个动作只完成一次.将这
三个动作中成功的跳跃个数记为 X,求 X的分布列和数学期望 E(X);
(III)在本赛季中,从四个跳跃动作 4T,4S,4F,4Lz中选出三个,使得该选手这三个动作中
“成功”的跳跃个数的期望最大,请直接写出这三个动作的名称.
5
(19) (本小题 15分)
已知函数 ( ) = ,其中 > 0.
(I)当 = 2 时,求曲线 = ( )在点(2, (2))处的切线方程;
(Ⅱ)求 y f ( x )的单调区间;
(III)当 1 < 2且 1 2 > 0时,判断 ( 1) (
1 1
2)与 的大小,并说明理由.1 2
(20) (本小题 15分)
x2 y2 3
设椭圆M : 1(a b 0),且离心率为 ,过点 P(4,0)的直线与椭圆交于 A,B
a2 b2 2
两点,当直线 AB经过椭圆中心O时, AB 4 .
(Ⅰ)求椭圆M 的方程;
(Ⅱ)已知点T (1,1),直线 AT 和直线 BT 分别与 y 轴交于C, D ,与 x 轴交于 E , F ,若
3S CDT S EFT ,求直线 AB的斜率.
(21) (本小题 15分)
an
{a } ,an为偶数,设正整数数列 n 满足 an 1 2 n 1,2,...... .
an+5,an为奇数.
(1)若 a6 1,请写出 a1所有可能的取值;
(2)记集合M a *n | n N ,且 a1不是 5的倍数,求证:1 M ;
*
(3)存在常数T,对于 n N 都有 an T an,求 a1所有可能的取值.
6
答案
一.选择题
1 2 3 4 5 6 7 8 9 10
D B A C D B D A B A
二.填空题
11. 1 i
12. 2 1, 2 1
13. 4 2,2 6
14. e, , 1 .
15. ①②③
三.解答题
16.【答案】解:(1)证明:在△ 中,∵ = 4, = 3, = 5,
∴ 2 + 2 = 2,∴ ⊥ ,
∵ 1 ⊥平面 , 平面 ,
∴ 1 ⊥ ,
又 ∩ 1 = , , 1 平面 1 ,
∴ ⊥平面 1 ,又 1 平面 1 ,
∴ ⊥ 1C. 5分
(2)由(1)可知, 1 ⊥平面 , , 平面 ,所以 1 ⊥ , 1 ⊥ ,
又 ⊥ ,
以 为原点,以 , , 1为坐标轴建立空间直角坐标系 ,如图所示,
则 (0,0,0), (0,3,0), (4,0,0), 1(0,0,4), (2,
3
2 , 0),
∴ ��� �� = (0,3,0), ��� ��1� = ( 4,0,4),� �� �� = ( 2,
3
2 , 0),
7
∵ ⊥平面 1 ,∴ � �� ��是平面 1 的一个法向量,
设平面 1的法向量为� � = ( , , ),
� � ��� ��1� = 0 4 + 4 = 0则 ,即 3 ,解得 =
4
2 + = 0 3 ,� � ��� �� = 0 2 =
令 = 1 4可得� � = (1, 3 , 1),
�����
∴ cos < � �, ��� �� >= � � = 4 2 34
| ��|| ��� ��| 34
=
×3 17
,
3
由图形可知二面角 1 为锐二面角,
∴二面角 1 的余弦值为
2 34. 11分
17
(3)由(2)可知,� ��1� ���1� = ��� �� = (0,3,0),
设 1 1与平面 1 所成角为 ,
则 = |cos < � ��1� ���1�,� � > | =
2 34,
17
∴ 1到平面 1 的距离为|� ��1� ���1�| = 3 ×
2 34 = 6 34. 14分17 17
(17)解:(Ⅰ) f (x) Asin( x )过 (0,1)
结合图象,有:1 2sin
则由0 π π ,有
2 6
π
所以 A 2, 【5分】
6
(Ⅱ)选择条件①
MN 5 xM xN 3
T π
则 3 π
2 3
f (x) π π故 2sin( x )
3 6
π 2kπ π x π π令 2kπ,
2 3 6 2
有 2 6k x 1 6k ,
所以 f (x)单调递增区间为[ 2 6k ,1 6k ], k Z 【13分】
8
选择条件②
OM 5 xM 1 M (1,2)
则 2 2sin( π )
6
π π
由0 ,有
2 3
f (x) π π故 2sin( x )
3 6
以下同①
选择条件③
f (5) 0 sin(5 π) 0 2kπ π (k Z ),
2 2 6 5 15
由0 π π ,有
2 3
故 f (x) 2sin( π x π )
3 6
以下同①
5
(18)(1)
7
179
(2)分布列见解析,数学期望为
84
(3)4T,4S, 4F
【分析】(1)根据题意,结合表格的数据,结合古典概型的概率公式代入计算,即可得到结果;
(2)根据题意,由条件可得 X的所有可能取值为 0,1,2,3,然后分别计算对应的概率,即可得
到分布列,再由期望的计算公式即可得到结果.
(3)根据题意,结合表格中的数据即可得到结果.
【详解】(1)根据题中数据,该选手上一赛季 7个 4T动作中,有 5个跳跃为“成功”,所以从该
5
选手上一赛季所有 4T动作中任选一次,这次跳跃“成功”的概率可以估计为 . 4分
7
(2)同(1),从该选手上一赛季所有 4S,4F动作中分别任选一次,这次跳跃“成功”的概率分
2
别可以估计为 ,
3
,
3 4
X的所有可能取值为 0,1,2,3.
P X 0 1 5 1 2 3 1
1 ,
7 3 4 42
9
P X 1 5 2 3 5 1 1 1 2 1 3 1 5 1 2 3 5
7 3
,
4 7 3 4 7 3 4 28
P X 2 5 2 3 5 2 3 5 2 3 37 5 2 3 5
7 3
1 1 1 , P X 3 .
4 7 3 4 7 3 4 84 7 3 4 14
所以随机变量 X的分布列为:
X 0 1 2 3
1 5 37 5
P
42 28 84 14
所以 E X 0 1 5 37 1 2 3 5 179 . 10分
42 28 84 14 84
5 2
(3)由表格可知,4T动作成功的概率为 ,失败的概率为 ,
7 7
2 1
4S动作成功的概率为 ,失败的概率为 ,
3 3
3
4F 1动作成功的概率为 ,失败的概率为 ,
4 4
3 2
4Lz动作成功的概率为 ,失败的概率为 ,
5 5
3 5 2 3
由 可知,选 4T,4S, 4F. 13分
4 7 3 5
2 2
(19)解:(1)当 = 2 时, ( ) = ; '( ) = (2 1)
2
;
4 4
而 (2) = , '(2) = 3 ;
2 4
4 3 4 3 4
故曲线 = ( )在点(2, (2))处的切线方程为 = ( 2),即 = 4. 4分
2 4 4
' ( 1) (2) ( )的定义域为( ∞,0) ∪ (0, + ∞),且 ( ) = ;令 '2 ( ) = 0,
1
得 = .
当 变化时, '( )与 ( )的变化情况如下表:
( ∞,0) 1 1 1(0, ) ( , + ∞)
'( ) 0 +
( ) 单调递减 单调递减 极小值 单调递增
所以 ( ) ( 1的单调递增区间为 , + ∞);单调递减区间为( ∞,0) 1和(0, ); 9分
(3)当 < 且 > 0 1 1时, 1 2 < ,证明如下: 1 2
10
= 1 , ' = 1
+1
令 则
2
.
设 = 1 + 1,则 ' = .
所以当 x∈(--∞,0)时, ' < 0;当 ∈ 0 +∞ 时, ' > 0.
所以 h(x)在(--∞,0)上单调递减,在( 0 +∞ 上单调递增.
从而 h(x)>h(0)=0,即 ' > 0,
所以 g(x)的单调递增区间为(--∞,0)和( 0 +∞ .
当 0 < < 时, < ,即 1 <
1 12 ; 1 2
当 1 <
1 1
2 < 0 时, < ,即 1 2 < . 1 2
综上,当 1 < 2且 1 2 > 0时, ( 1) ( ) <
1 1
2 . 15分 1 2
2a 4 a 2 x2
(20)解:(Ⅰ ) 1 ,所以M : y2 1; 5分
2a 2b 4 b 1 4 2
(Ⅱ)①当直线 AB的方程为 = 0时,显然 A( 2,0), B(2,0);
直线 AT 的方程为 = + 2, 2所以 C(0, );
3 3 3
直线 BT的方程为 = + 2,所以 D(0,2);
此时点 E与点 A重合,点 F与点 B重合,易知3S CDT S EFT ;
②设直线 AB : x my 4, A(x1, y1),B(x2, y2)
x2 4y2 4
(m2 4)y2 8my 12 0,
x my 4
64m2 48(m2 4) 0 m2,即 12 0,也即m 2 3或m 2 3 3 3,k ( , );
6 6
y 8m 121 y2 2 , y1y ;m 4 2 m2 4
x x 32
2
1 2 2 , x1x
4m 64
2 ;m 4 m2 4
3S CDT S EFT 3CD EF 3 yC yD xE xF
11
直线 AT : y 1 y1 1 y 1 (x 1),直线 BT : y 1 2 (x 1)
x1 1 x2 1
令 x 0,C(0, y 1 1 1),D(0, y 2 1 1)
x1 1 x2 1
y 0 E( x1 1令 , 1,0) x 1, F ( 2 1,0)
y1 1 y2 1
3 y1 1 y则 2 1 x1 1 x 1 2
x1 1 x2 1 y1 1 y2 1
即 x1x2 (x1 x2 ) 1 3 y1y2 (y1 y2 ) 1
也即 4m2 64 32 m2 4 3 12 8m m2 4
3m2 36 3 m2 8m 16
则 24m 84 0 7,m 2 3 3,斜率为 ( , );
2 7 6 6
综上,直线 AB的斜率为 0或 2 . 15分
7
(21)(1)a1 6,a1 11,a1 32 4分
(2)设 t中最小数为ak t, t,k N
*
t
①当 t为偶数时, ak 1 t与 t是最小值矛盾2
t 5
②当 t为奇数时,ak 1 t 5是偶数, ak 2 t2
t 5
t 1或3或5.
1)当 t 5时, ak 1也是5的倍数,以此类推…, a1也是5的倍数,与 a1不是 5的倍数
矛盾.
2)当 t 3时,ak 1 8,ak 2 4,ak 3 2,ak 4 1 t,矛盾,
t 1,即1 M成立. 9分
(3)由第(2)问可知, an 中最小数只能是1或 5.
12
当 t 1时,后面的项为6,3,8,4,2,1……
当 t 5时,后面的项为10,5,10,5……
所以数列 an 为周期数列时,只能是1,2,3,4,5,6,8,10
所以a1 {1,2,3,4,5,6,8,10} 15分
13
14
同课章节目录
