湘教版八年级数学下册:2.5.2矩形的判定(共20张PPT)
文档属性
| 名称 | 湘教版八年级数学下册:2.5.2矩形的判定(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-19 00:00:00 | ||
图片预览





文档简介
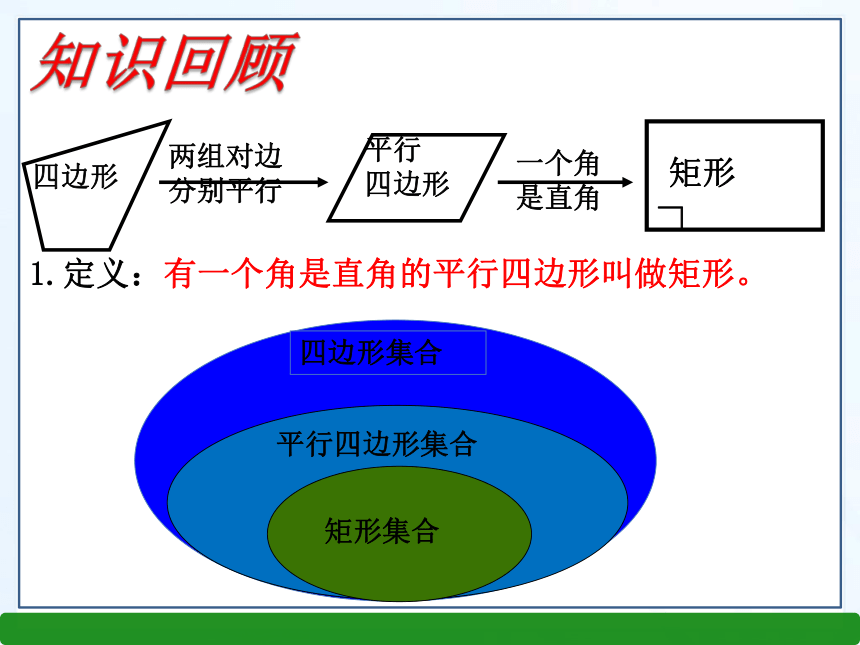
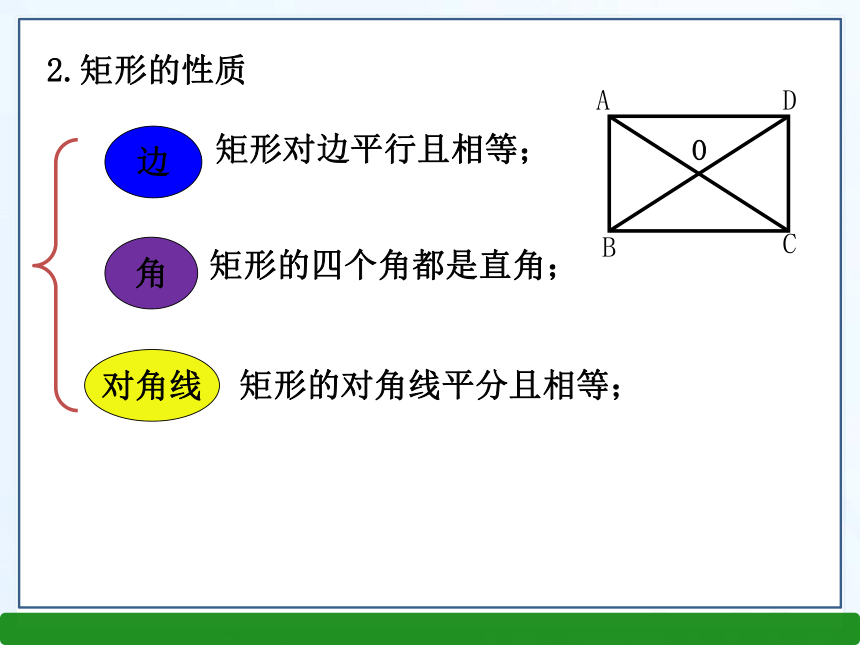
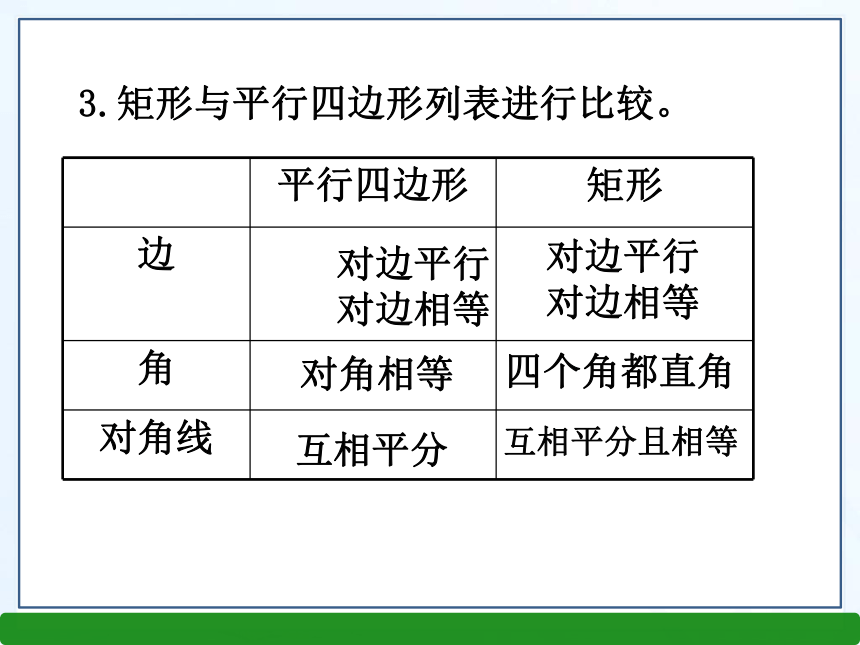
课件20张PPT。2.5.2矩形的判定第2章 四边形1.定义:有一个角是直角的平行四边形叫做矩形。知识回顾边对角线角矩形对边平行且相等;矩形的四个角都是直角;矩形的对角线平分且相等;2.矩形的性质3.矩形与平行四边形列表进行比较。 对边平行
对边相等对边平行
对边相等对角相等四个角都直角互相平分互相平分且相等小明利用周末的时间,为自己做了一个相框. 请你利用直尺和三角板帮他检验一下,相框是矩形吗?
除了矩形的定义外,有没有其他判定矩形的方法呢? 情境引入1.矩形的定义:有一个角是直角的平行四边形是矩形。你还有其它的判定方法吗?∠A=900四边形ABCD是矩形自主预习有一个角是直角
有两个角是直角 的四边形是矩形吗?
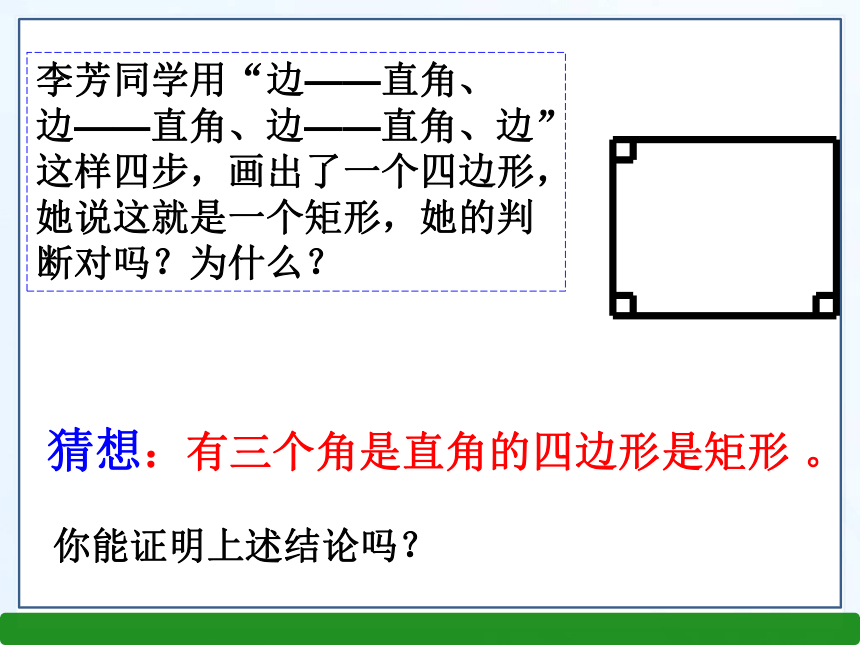
有三个角是直角新知探究李芳同学用“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?猜想:有三个角是直角的四边形是矩形 。你能证明上述结论吗?已知:在四边形ABCD中,∠A=∠B=∠C=90°
求证:四边形ABCD是矩形。证明:∵ ∠A=∠B=90°∴ ∠A+∠B=180°∴AD∥BC同理可证:AB∥CD∴四边形ABCD是平行四边形又∵ ∠A=90°∴四边形ABCD是矩形你还有其它的证明方法吗?判定定理1.有三个角是直角的四边形是矩形 。 ∵ ∠A=∠B=∠C=90°
∴ 四边形ABCD是矩形几何语言:O如果一个平行四边形的对角线变成相等呢?将AC同时向两边拉长,使AC=BD 交流:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?猜想:对角线相等的平行四边形是矩形 。已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。证明: ∵ AB=CD, BC=BC, AC=BD∴ △ABC≌ △DCB(SSS)∵ AB//CD
∴ ∠ABC+∠DCB=180° ∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形∴四边形ABCD是矩形。∴ ∠ABC=∠DCB对角线相等的平行四边形是矩形 。定理2.几何语言:∵四边形ABCD是平行四边形
AC=BD∴四边形ABCD是矩形(对角线相等且互相平分的四边形是矩形。)(或OA=OC=OB=OD)例2 如图,在 ABCD 中,它的两条对角线相交于点O。
(1)如果 ABCD 是矩形,试问: △OBC是什么样的三角形?
(2)如果△OBC是等腰三角形,其中:OB=OC,那么 ABCD是矩形吗?你能归纳矩形的几种判定方法吗?有一个角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形 。(对角线相等且互相平分的四边形是矩形。)有三个角是直角的四边形是矩形 。方法1:方法2:方法3:知识梳理×√×√√一. 现在你能帮小明解决问题了吗?小明判定
矩形的下列方法中哪些正确?为什么?
1.有一个角是直角的四边形是矩形; ( )
2.四个角都相等的四边形是矩形; ( )
3.对角线相等的四边形是矩形; ( )
4.对角线互相平分且相等的四边形是矩形;( )
5.两组对边分别平行,且对角线相等的四边
形是矩形. ( ) 随堂练习C5C1.能够判断一个四边形是矩形的条件是( )
A 对角线相等 B 对角线垂直
C对角线互相平分且相等 D对角线垂直且相等
2.矩形的一组邻边长分别是3cm和4cm,则它的对角线长是 cm
3.如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠ EAC、 ∠ MCA、 ∠ ACN、 ∠ CAF的角平分线,则四边形ABCD是( )
A 菱形 B 平行四边形
C 矩形 D 不能确定1.如图,M为平行四边形ABCD边AD的中点,且MB=MC,
求证:四边形ABCD是矩形。 要判定一个四边形是矩形,通常先判定它是平行四边形,再根据平行四边形构成矩形的条件,判定有一个角是直角或者对角线相等。练习三 观察可能导致发现,观察将揭示某种规则、模式或定律。
——波利亚结束语
对边相等对边平行
对边相等对角相等四个角都直角互相平分互相平分且相等小明利用周末的时间,为自己做了一个相框. 请你利用直尺和三角板帮他检验一下,相框是矩形吗?
除了矩形的定义外,有没有其他判定矩形的方法呢? 情境引入1.矩形的定义:有一个角是直角的平行四边形是矩形。你还有其它的判定方法吗?∠A=900四边形ABCD是矩形自主预习有一个角是直角
有两个角是直角 的四边形是矩形吗?
有三个角是直角新知探究李芳同学用“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?猜想:有三个角是直角的四边形是矩形 。你能证明上述结论吗?已知:在四边形ABCD中,∠A=∠B=∠C=90°
求证:四边形ABCD是矩形。证明:∵ ∠A=∠B=90°∴ ∠A+∠B=180°∴AD∥BC同理可证:AB∥CD∴四边形ABCD是平行四边形又∵ ∠A=90°∴四边形ABCD是矩形你还有其它的证明方法吗?判定定理1.有三个角是直角的四边形是矩形 。 ∵ ∠A=∠B=∠C=90°
∴ 四边形ABCD是矩形几何语言:O如果一个平行四边形的对角线变成相等呢?将AC同时向两边拉长,使AC=BD 交流:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?猜想:对角线相等的平行四边形是矩形 。已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。证明: ∵ AB=CD, BC=BC, AC=BD∴ △ABC≌ △DCB(SSS)∵ AB//CD
∴ ∠ABC+∠DCB=180° ∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形∴四边形ABCD是矩形。∴ ∠ABC=∠DCB对角线相等的平行四边形是矩形 。定理2.几何语言:∵四边形ABCD是平行四边形
AC=BD∴四边形ABCD是矩形(对角线相等且互相平分的四边形是矩形。)(或OA=OC=OB=OD)例2 如图,在 ABCD 中,它的两条对角线相交于点O。
(1)如果 ABCD 是矩形,试问: △OBC是什么样的三角形?
(2)如果△OBC是等腰三角形,其中:OB=OC,那么 ABCD是矩形吗?你能归纳矩形的几种判定方法吗?有一个角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形 。(对角线相等且互相平分的四边形是矩形。)有三个角是直角的四边形是矩形 。方法1:方法2:方法3:知识梳理×√×√√一. 现在你能帮小明解决问题了吗?小明判定
矩形的下列方法中哪些正确?为什么?
1.有一个角是直角的四边形是矩形; ( )
2.四个角都相等的四边形是矩形; ( )
3.对角线相等的四边形是矩形; ( )
4.对角线互相平分且相等的四边形是矩形;( )
5.两组对边分别平行,且对角线相等的四边
形是矩形. ( ) 随堂练习C5C1.能够判断一个四边形是矩形的条件是( )
A 对角线相等 B 对角线垂直
C对角线互相平分且相等 D对角线垂直且相等
2.矩形的一组邻边长分别是3cm和4cm,则它的对角线长是 cm
3.如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠ EAC、 ∠ MCA、 ∠ ACN、 ∠ CAF的角平分线,则四边形ABCD是( )
A 菱形 B 平行四边形
C 矩形 D 不能确定1.如图,M为平行四边形ABCD边AD的中点,且MB=MC,
求证:四边形ABCD是矩形。 要判定一个四边形是矩形,通常先判定它是平行四边形,再根据平行四边形构成矩形的条件,判定有一个角是直角或者对角线相等。练习三 观察可能导致发现,观察将揭示某种规则、模式或定律。
——波利亚结束语
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
