湘教版八年级数学下册:2.6.1菱形的性质(共17张PPT)
文档属性
| 名称 | 湘教版八年级数学下册:2.6.1菱形的性质(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-20 00:00:00 | ||
图片预览





文档简介
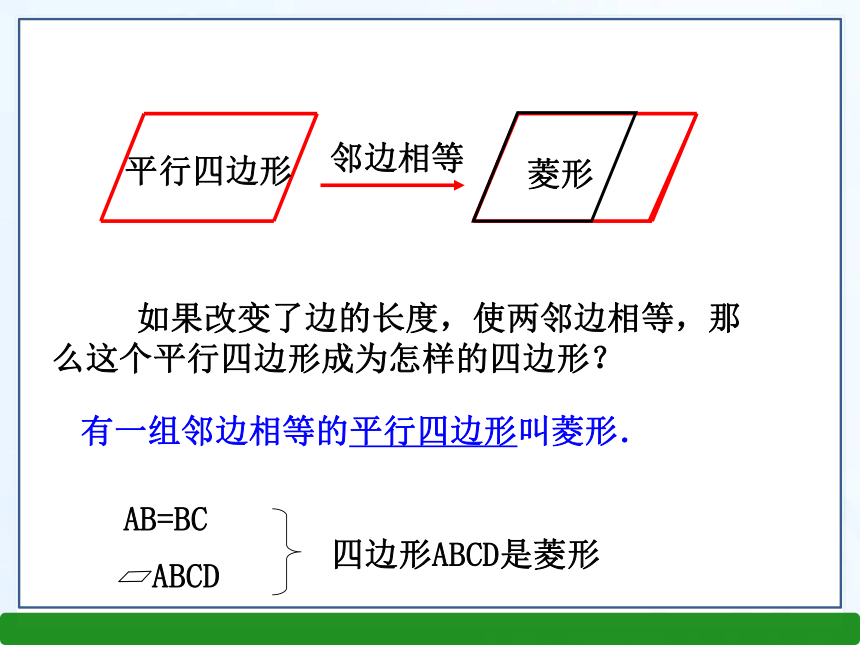
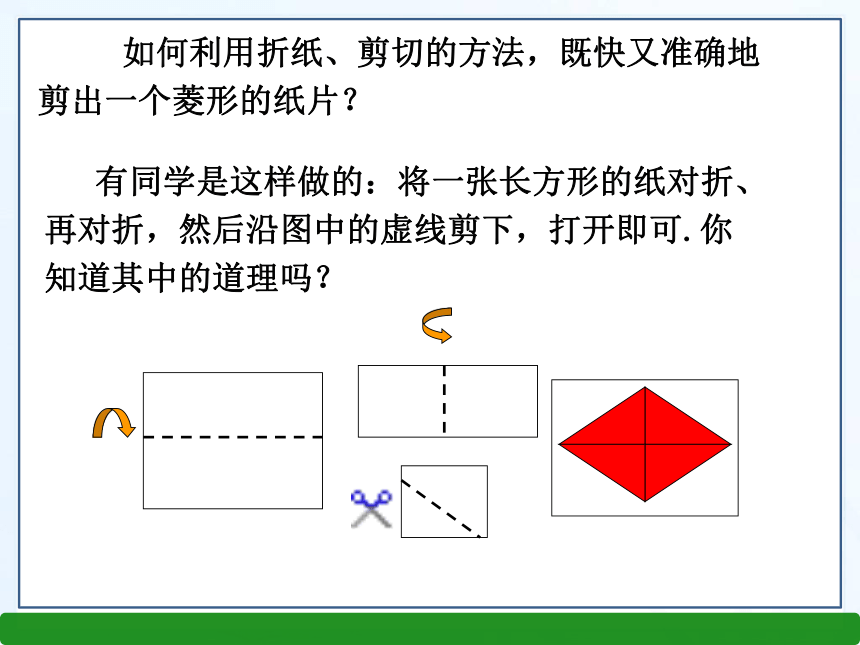
课件17张PPT。2.6.1菱形的性质第2章 前面我们学习了平行四边形和矩形,知道了如果平行四边形有一个角是直角时,成为什么图形?(矩形,由角变化得到) 如果从边的角度,将平行四边形特殊化,又会得到什么特殊的四边形呢?知识回顾 平行四边形 邻边相等 在平行四边形中,如果内角大小保持不变,仅改变边的长度,请仔细观察和思考,在这变化过程中,哪些关系没变?哪些关系变了? 如果改变了边的长度,使两邻边相等,那么这个平行四边形成为怎样的四边形?情境引入有一组邻边相等的平行四边形叫菱形. 平行四边形 邻边相等菱形 如果改变了边的长度,使两邻边相等,那么这个平行四边形成为怎样的四边形?AB=BC四边形ABCD是菱形让我们一同走进生活中的菱形 有同学是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗? 如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?菱形是轴对称图形 观察得到的菱形,它是中心对称图形吗?它是
轴对称图形吗?如果是,有几条对称轴?对称轴
之间有什么位置关系?菱形是中心对称图形自主预习从图中你能得到哪些结论?并说明理由.提示:从边、角、对角线、面积等方面来探讨 观察得到的菱形,它是中心对称图形吗?、它是轴对
称图形吗?如果是,有几条对称轴?对称轴之间有什么
位置关系?新知探究 由于平行四边形的对边相等,而菱形的邻边相等,
故:性质2:
菱形的对角线互相垂直。 菱形是特殊的平行四边形,具有平行四边形的所有性质.性质1:
菱形的四条边都相等。又:已知:菱形ABCD的对角线AC和BD相交于点O,如下图,证明:∵四边形ABCD是菱形在△ABD中,∵BO=DO∴AB=AD(菱形的四条边都相等)∴AC⊥BD,AC平分∠BAD同理: AC平分∠BCD;
BD平分∠ABC和∠ADC求证:AC⊥BD ;
AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC 命题:菱形的对角线互相垂直平分,
并且每一条对角线平分一组对角。例1.已知菱形ABCD的两条对角线AC,BD的长度分别为4cm,3cm,求菱形ABCD的面积和周长。
解:菱形ABCD的面积为
S= ×4 ×3=6(cm2 )在Rt △ ABO中,
OA= AC= ×4=2(cm),OB=
所以,AB=
因此,菱形ABCD的周长为2.5 ×4=10(cm)性质2.
菱形的对角线互相垂直。数学语言性质1.
菱形的四条边都相等。∵四边形ABCD是菱形 ∴ AB=BC=CD=DA∴ AC⊥BD 知识梳理1.如图,在菱形ABCD中,对角线AC、BD相交于点O。(2)有哪些特殊的三角形?(1)图中有哪些线段是相等的?哪些角是相等的?随堂练习2.已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=1。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。3.四边形ABCD是菱形,O是两条对角线的交点,已知AB=5cm,AO=4cm,求对角线BD的长。解:∵四边形ABCD是菱形∴AC⊥BD∴∴OB=3∴ BD=2OB=6 cm543 有关菱形问题可转化为直角三角形或等腰三角形的问题来解决4.已知:如图,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F.
求证:EF⊥AD; 5.如图,E为菱形ABCD边BC上一点,且AB=AE,AE交BD于O,且∠DAE=2∠BAE,
求证:EB=OA。
轴对称图形吗?如果是,有几条对称轴?对称轴
之间有什么位置关系?菱形是中心对称图形自主预习从图中你能得到哪些结论?并说明理由.提示:从边、角、对角线、面积等方面来探讨 观察得到的菱形,它是中心对称图形吗?、它是轴对
称图形吗?如果是,有几条对称轴?对称轴之间有什么
位置关系?新知探究 由于平行四边形的对边相等,而菱形的邻边相等,
故:性质2:
菱形的对角线互相垂直。 菱形是特殊的平行四边形,具有平行四边形的所有性质.性质1:
菱形的四条边都相等。又:已知:菱形ABCD的对角线AC和BD相交于点O,如下图,证明:∵四边形ABCD是菱形在△ABD中,∵BO=DO∴AB=AD(菱形的四条边都相等)∴AC⊥BD,AC平分∠BAD同理: AC平分∠BCD;
BD平分∠ABC和∠ADC求证:AC⊥BD ;
AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC 命题:菱形的对角线互相垂直平分,
并且每一条对角线平分一组对角。例1.已知菱形ABCD的两条对角线AC,BD的长度分别为4cm,3cm,求菱形ABCD的面积和周长。
解:菱形ABCD的面积为
S= ×4 ×3=6(cm2 )在Rt △ ABO中,
OA= AC= ×4=2(cm),OB=
所以,AB=
因此,菱形ABCD的周长为2.5 ×4=10(cm)性质2.
菱形的对角线互相垂直。数学语言性质1.
菱形的四条边都相等。∵四边形ABCD是菱形 ∴ AB=BC=CD=DA∴ AC⊥BD 知识梳理1.如图,在菱形ABCD中,对角线AC、BD相交于点O。(2)有哪些特殊的三角形?(1)图中有哪些线段是相等的?哪些角是相等的?随堂练习2.已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=1。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。3.四边形ABCD是菱形,O是两条对角线的交点,已知AB=5cm,AO=4cm,求对角线BD的长。解:∵四边形ABCD是菱形∴AC⊥BD∴∴OB=3∴ BD=2OB=6 cm543 有关菱形问题可转化为直角三角形或等腰三角形的问题来解决4.已知:如图,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F.
求证:EF⊥AD; 5.如图,E为菱形ABCD边BC上一点,且AB=AE,AE交BD于O,且∠DAE=2∠BAE,
求证:EB=OA。
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
