广东省深圳市福田外国语学校2024-2025学年九年级(上)期中数学试卷(含答案)
文档属性
| 名称 | 广东省深圳市福田外国语学校2024-2025学年九年级(上)期中数学试卷(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 935.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-18 00:00:00 | ||
图片预览



文档简介
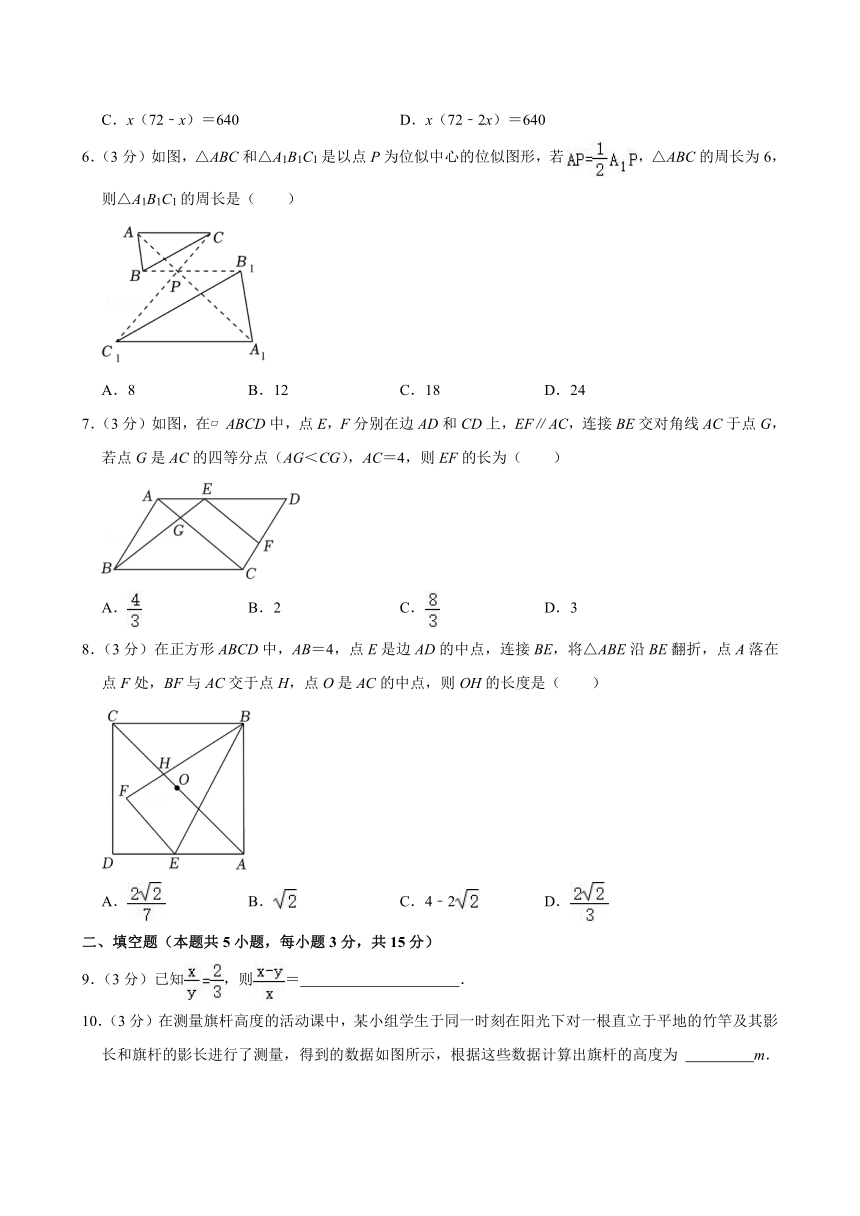
2024-2025学年广东省深圳市福田外国语学校九年级(上)期中数学试卷
一、选择题(本大题共8小题,每小题3分,共24分,每小题有四个选项,其中只有一个是正确的)
1.(3分)如图所示的几何体,其俯视图是( )
A. B.
C. D.
2.(3分)在传统游戏“石头、剪子、布”中,随机出一个手势,出“石头”的概率是( )
A. B. C. D.
3.(3分)不解方程,判断方程x2﹣4x﹣1=0的根的情况是( )
A.没有实数根 B.有两个相等实数根
C.有两个不相等实数根 D.无法确定
4.(3分)如图,在△ABC中,DE∥BC,,DE=4,则BC的长是( )
A.8 B.10 C.11 D.12
5.(3分)如图,张老汉想用长为70米的栅栏,再借助房屋的外墙(外墙足够长)围成一个面积为640平方米的矩形羊圈ABCD,并在边BC上留一个2米宽的门(建在EF处,门用其他材料),设AB的长为x米,则下面所列方程正确的是( )
A.x(70﹣x)=640 B.x(70﹣2x)=640
C.x(72﹣x)=640 D.x(72﹣2x)=640
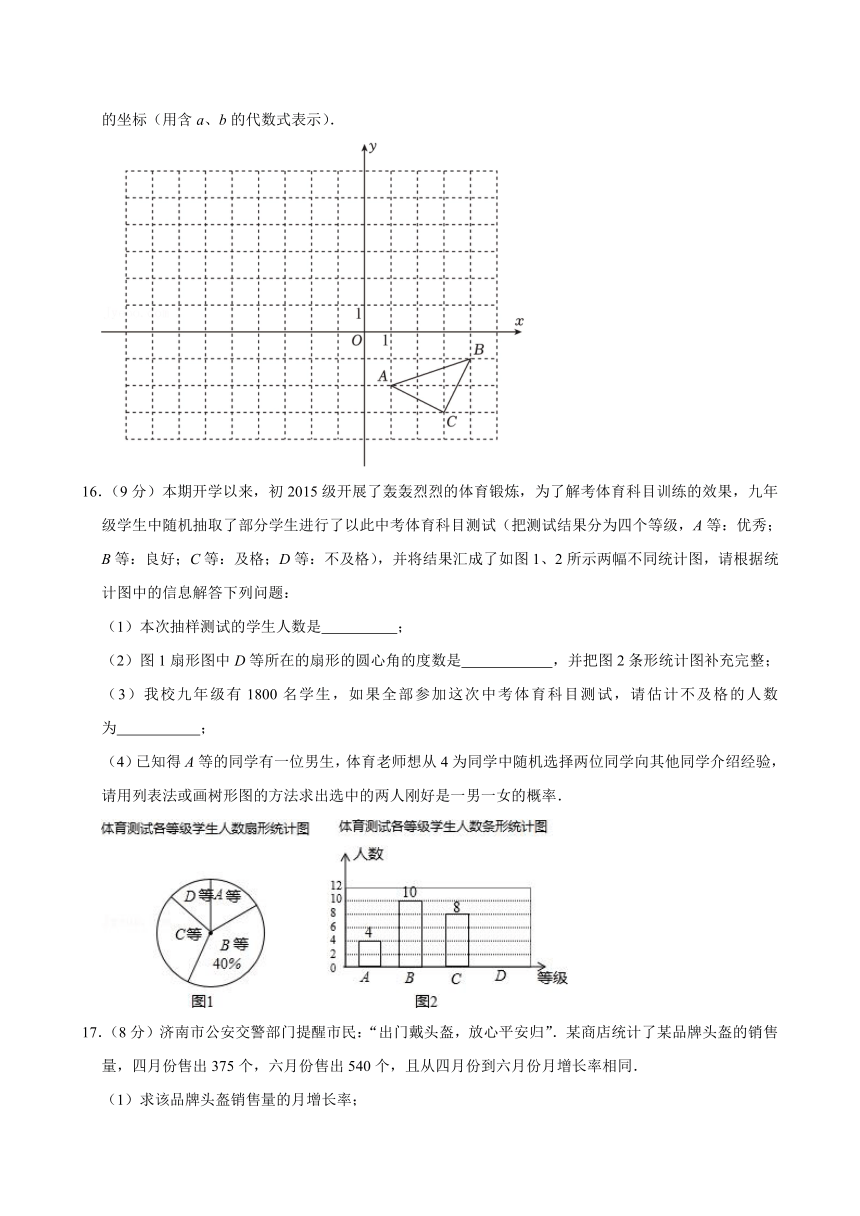
6.(3分)如图,△ABC和△A1B1C1是以点P为位似中心的位似图形,若,△ABC的周长为6,则△A1B1C1的周长是( )
A.8 B.12 C.18 D.24
7.(3分)如图,在 ABCD中,点E,F分别在边AD和CD上,EF∥AC,连接BE交对角线AC于点G,若点G是AC的四等分点(AG<CG),AC=4,则EF的长为( )
A. B.2 C. D.3
8.(3分)在正方形ABCD中,AB=4,点E是边AD的中点,连接BE,将△ABE沿BE翻折,点A落在点F处,BF与AC交于点H,点O是AC的中点,则OH的长度是( )
A. B. C.4﹣2 D.
二、填空题(本题共5小题,每小题3分,共15分)
9.(3分)已知,则= .
10.(3分)在测量旗杆高度的活动课中,某小组学生于同一时刻在阳光下对一根直立于平地的竹竿及其影长和旗杆的影长进行了测量,得到的数据如图所示,根据这些数据计算出旗杆的高度为 m.
11.(3分)一个不透明的箱子里有3个球,其中2个白球,1个红球,它们除了颜色外其他都相同,从中任意摸出一个球,记下颜色后放回,搅匀,再摸出一个球,则摸出的两个球恰好颜色不同的概率为 .
12.(3分)如图,Rt△ABC中,∠ABC=90°,BD⊥AC,垂足为D,AE平分∠BAC,分别交BD,BC于点F,E.若AB:BC=3:4,则= .
13.(3分)在菱形ABCD中,E,F分别是AB,BC边上的中点,G为DE上一点,若AB=6,∠B=∠EGF=60°,则DG的长为 .
三、解答题(本题共7小题,其中第14题6分,第15题6分,第16题9分,第17题8分,第18题8分,第19题12分,第20题12分,共61分)
14.(6分)解一元二次方程:
(1)(x+2)2=3(x+2);
(2)x2﹣3x﹣1=0.
15.(6分)如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(1,﹣2)、B(4,﹣1),C(3,﹣3).
(1)画出将△ABC向左平移5个单位,再向上平移3个单位后的△A1B1C1;
(2)以原点O为位似中心,在位似中心的同侧画出△A1B1C1的一个位似△A2B2C2,使它与△A1B1C1的相似比为2:1;
(3)若△A1B1C1内部任意一点P1的坐标为(a,b),直接写出经过(2)的变化后点P1的对应点P2的坐标(用含a、b的代数式表示).
16.(9分)本期开学以来,初2015级开展了轰轰烈烈的体育锻炼,为了解考体育科目训练的效果,九年级学生中随机抽取了部分学生进行了以此中考体育科目测试(把测试结果分为四个等级,A等:优秀;B等:良好;C等:及格;D等:不及格),并将结果汇成了如图1、2所示两幅不同统计图,请根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 ;
(2)图1扇形图中D等所在的扇形的圆心角的度数是 ,并把图2条形统计图补充完整;
(3)我校九年级有1800名学生,如果全部参加这次中考体育科目测试,请估计不及格的人数为 ;
(4)已知得A等的同学有一位男生,体育老师想从4为同学中随机选择两位同学向其他同学介绍经验,请用列表法或画树形图的方法求出选中的两人刚好是一男一女的概率.
17.(8分)济南市公安交警部门提醒市民:“出门戴头盔,放心平安归”.某商店统计了某品牌头盔的销售量,四月份售出375个,六月份售出540个,且从四月份到六月份月增长率相同.
(1)求该品牌头盔销售量的月增长率;
(2)经市场调研发现,此种品牌头盔如果每个盈利10元,月销售量为500个,若在此基础上每个涨价1元,则月销售量将减少20个,现在既要使月销售利润达到6000元,又要尽可能让顾客得到实惠,那么该品牌头盔每个应涨价多少元?
18.(8分)如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E.
(1)求证:四边形ABCD是菱形;
(2)若,BD=2,求BE的长.
19.(12分)在数学综合与实践活动课上,同学们用两个完全相同的矩形纸片展开探究活动:
【实践探究】:(1)小红将两个矩形纸片摆成图1的形状,连接AG、AC,则∠ACG= °;
【解决问题】:(2)将矩形AQGF绕点A顺时针转动,边AF与边CD交于点M,连接BM,AB=10,AD=6.
①如图2,当BM=AB时,求证:AM平分∠DMB;写出证明过程
②如图3,当点F落在DC上时,连接BQ交AF于点O,则AO= ;
【迁移应用】:(3)如图4,正方形ABCD的边长为,E是BC边上一点(不与点B、C重合),连接AE,将线段AE绕点E顺时针旋转90°至FE,作射线FC交AB的延长线于点G,则BG= ;
(4)如图5,在菱形ABCD中,∠A=120°,E是CD边上一点(不与点C、D重合),连接BE,将线段BE绕点E顺时针旋转120°至FE,作射线FD交BC的延长线于点G,若,则CG= .
20.(12分)在正方形ABCD中,AB=10,AC是对角线,点O是AC的中点,点E在AC上,连接DE,点C关于DE的对称点是C′,连接DC′,EC′.
(1)如图1,若DC′经过点O,求证:;
(2)如图2,连接CC′,BC′,若∠ADC′=2∠CBC′,求CC′的长;
(3)当点B,C′,E三点共线时,直接写出CE的长.
2024-2025学年广东省深圳市福田外国语学校九年级(上)期中数学试卷
参考答案
一、选择题(本大题共8小题,每小题3分,共24分,每小题有四个选项,其中只有一个是正确的)
1.(3分)如图所示的几何体,其俯视图是( )
A. B.
C. D.
选:B.
2.(3分)在传统游戏“石头、剪子、布”中,随机出一个手势,出“石头”的概率是( )
A. B. C. D.
选:C.
3.(3分)不解方程,判断方程x2﹣4x﹣1=0的根的情况是( )
A.没有实数根 B.有两个相等实数根
C.有两个不相等实数根 D.无法确定
选:C.
4.(3分)如图,在△ABC中,DE∥BC,,DE=4,则BC的长是( )
A.8 B.10 C.11 D.12
选:D.
5.(3分)如图,张老汉想用长为70米的栅栏,再借助房屋的外墙(外墙足够长)围成一个面积为640平方米的矩形羊圈ABCD,并在边BC上留一个2米宽的门(建在EF处,门用其他材料),设AB的长为x米,则下面所列方程正确的是( )
A.x(70﹣x)=640 B.x(70﹣2x)=640
C.x(72﹣x)=640 D.x(72﹣2x)=640
选:D.
6.(3分)如图,△ABC和△A1B1C1是以点P为位似中心的位似图形,若,△ABC的周长为6,则△A1B1C1的周长是( )
A.8 B.12 C.18 D.24
选:B.
7.(3分)如图,在 ABCD中,点E,F分别在边AD和CD上,EF∥AC,连接BE交对角线AC于点G,若点G是AC的四等分点(AG<CG),AC=4,则EF的长为( )
A. B.2 C. D.3
选:C.
8.(3分)在正方形ABCD中,AB=4,点E是边AD的中点,连接BE,将△ABE沿BE翻折,点A落在点F处,BF与AC交于点H,点O是AC的中点,则OH的长度是( )
A. B. C.4﹣2 D.
选:A.
二、填空题(本题共5小题,每小题3分,共15分)
9.(3分)已知,则= ﹣ .
10.(3分)在测量旗杆高度的活动课中,某小组学生于同一时刻在阳光下对一根直立于平地的竹竿及其影长和旗杆的影长进行了测量,得到的数据如图所示,根据这些数据计算出旗杆的高度为 12 m.
11.(3分)一个不透明的箱子里有3个球,其中2个白球,1个红球,它们除了颜色外其他都相同,从中任意摸出一个球,记下颜色后放回,搅匀,再摸出一个球,则摸出的两个球恰好颜色不同的概率为 .
12.(3分)如图,Rt△ABC中,∠ABC=90°,BD⊥AC,垂足为D,AE平分∠BAC,分别交BD,BC于点F,E.若AB:BC=3:4,则= .
13.(3分)在菱形ABCD中,E,F分别是AB,BC边上的中点,G为DE上一点,若AB=6,∠B=∠EGF=60°,则DG的长为 .
三、解答题(本题共7小题,其中第14题6分,第15题6分,第16题9分,第17题8分,第18题8分,第19题12分,第20题12分,共61分)
14.(6分)解一元二次方程:
(1)(x+2)2=3(x+2);
(2)x2﹣3x﹣1=0.
【解答】解:(1)(x+2)2=3(x+2),
(x+2)2﹣3(x+2)=0,
(x+2﹣3)(x+2)=0,
x+2﹣3=0或x+2=0,
解得x1=1,x2=﹣2;
(2)x2﹣3x﹣1=0,
x2﹣3x=1,
x2﹣3x+=1+,
=1+,
=,
x﹣=,
解得x1=,x2=.
15.(6分)如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(1,﹣2)、B(4,﹣1),C(3,﹣3).
(1)画出将△ABC向左平移5个单位,再向上平移3个单位后的△A1B1C1;
(2)以原点O为位似中心,在位似中心的同侧画出△A1B1C1的一个位似△A2B2C2,使它与△A1B1C1的相似比为2:1;
(3)若△A1B1C1内部任意一点P1的坐标为(a,b),直接写出经过(2)的变化后点P1的对应点P2的坐标(用含a、b的代数式表示).
【解答】解:(1)如图所示,△A1B1C1为所求三角形.
(2)如图所示,△A2B2C2为所求角形.
(3)由题意可知△A2B2C2∽△A2B2C2,且相似比为2:1,
∴当点P1的坐标为(a,b)时,对应点P2的坐标为:(2a,2b).
16.(9分)本期开学以来,初2015级开展了轰轰烈烈的体育锻炼,为了解考体育科目训练的效果,九年级学生中随机抽取了部分学生进行了以此中考体育科目测试(把测试结果分为四个等级,A等:优秀;B等:良好;C等:及格;D等:不及格),并将结果汇成了如图1、2所示两幅不同统计图,请根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 25人 ;
(2)图1扇形图中D等所在的扇形的圆心角的度数是 43.2° ,并把图2条形统计图补充完整;
(3)我校九年级有1800名学生,如果全部参加这次中考体育科目测试,请估计不及格的人数为 216人 ;
(4)已知得A等的同学有一位男生,体育老师想从4为同学中随机选择两位同学向其他同学介绍经验,请用列表法或画树形图的方法求出选中的两人刚好是一男一女的概率.
【解答】解:(1)本次抽样测试的学生人数为10÷40%=25(人);
(2)D等级的人数为25﹣4﹣10﹣8=3,
所以D等所在的扇形的圆心角的度数=360°×=43.2°,
条形统计图补充为:
(3)1800×=216(人),
所以估计不及格的人数为216人;
故答案为25人,43.2°,216人;
(4)画树状图为:
共有12种等可能的结果数,其中选中的两人刚好是一男一女的结果数为6,
所以选中的两人刚好是一男一女的概率==.
17.(8分)济南市公安交警部门提醒市民:“出门戴头盔,放心平安归”.某商店统计了某品牌头盔的销售量,四月份售出375个,六月份售出540个,且从四月份到六月份月增长率相同.
(1)求该品牌头盔销售量的月增长率;
(2)经市场调研发现,此种品牌头盔如果每个盈利10元,月销售量为500个,若在此基础上每个涨价1元,则月销售量将减少20个,现在既要使月销售利润达到6000元,又要尽可能让顾客得到实惠,那么该品牌头盔每个应涨价多少元?
【解答】解:(1)设该品牌头盔销售量的月增长率x,
由题意得:375(1+x)2=540,
解得x1=0.2=20%,x2=﹣2.2(不合题意,舍去),
答:该品牌头盔销售量的月增长率为20%;
(2)设该品牌头盔每个应涨价m元,
由题意得:(10+m)(500﹣20m)=6000,
整理得:m2﹣15m+50=0,
解得m1=5,m2=10,
∵要尽可能让顾客得到实惠,
∴m=5,
答:该品牌的头盔每个应涨价5元.
18.(8分)如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E.
(1)求证:四边形ABCD是菱形;
(2)若,BD=2,求BE的长.
【解答】(1)证明:∵AB∥DC,
∴∠OAB=∠DCA,
∵AC平分∠DAB,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,则AD=CD,
又∵AB=AD,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AB=AD,
∴四边形ABCD是菱形.
(2)解:∵四边形ABCD是菱形,
∴,BD⊥AC,,,
由勾股定理可得:,
∵CE⊥AB,
在Rt△BCE中,CE2=BC2﹣BE2,
在Rt△ACE中,CE2=AC2﹣AE2=AC2﹣(AB+BE)2,
∴BC2﹣BE2=AC2﹣(AB+BE)2,即:,
解得:.
19.(12分)在数学综合与实践活动课上,同学们用两个完全相同的矩形纸片展开探究活动:
【实践探究】:(1)小红将两个矩形纸片摆成图1的形状,连接AG、AC,则∠ACG= 45 °;
【解决问题】:(2)将矩形AQGF绕点A顺时针转动,边AF与边CD交于点M,连接BM,AB=10,AD=6.
①如图2,当BM=AB时,求证:AM平分∠DMB;写出证明过程
②如图3,当点F落在DC上时,连接BQ交AF于点O,则AO= 4 ;
【迁移应用】:(3)如图4,正方形ABCD的边长为,E是BC边上一点(不与点B、C重合),连接AE,将线段AE绕点E顺时针旋转90°至FE,作射线FC交AB的延长线于点G,则BG= 5 ;
(4)如图5,在菱形ABCD中,∠A=120°,E是CD边上一点(不与点C、D重合),连接BE,将线段BE绕点E顺时针旋转120°至FE,作射线FD交BC的延长线于点G,若,则CG= 2 .
【解答】(1)解:∵长方形纸片ABCD和AFGQ是两个完全相同的长方形,
∴AC=AG,∠BAC=∠GAF,
∴∠BAC+∠CAD=∠GAF+∠CAD,
∴∠GAC=∠BAD=90°,
∴△ACG是等腰直角三角形,
∴∠ACG=45°,
故答案为:45;
(2)①证明:∵BM=AB,
∴∠BMA=∠BAM,
∵四边形ABCD是矩形,
∴AB∥DC,
∴∠DMA=∠MAB;
∴∠BMA=∠DMA,
∴AM平分∠DMB;
②解:过点B作BE⊥AF于点E,
∵AF=AB=10,AD=6,
∴DF==8,
∴CF=DC﹣DF=2,
∵AB=AF,
∴∠AFB=∠ABF,
∵AB∥CD,
∴∠ABF=∠CFB,
∴∠AFB=∠CFB,
∵BF=BF,∠C=∠BEF=90°,
∴△BCF≌△BEF(AAS),
∴CF=EF=2,BC=BE,
∴AE=8,
∵AD=AQ=BC,
∴AQ=BE,
∵∠QAO=∠BEO,∠AOQ=∠BOE,
∴△AOQ≌△EOB(AAS),
∴AO=OE=AE=4,
故答案为:4;
(3)解:如图4,过点F作FH⊥CD交CD于点H,
∵四边形ABCD是正方形,
∴CB=AB,∠ABC=90°,
∴∠H=∠ABC=90°,
由旋转的性质得:∠AEF=90°,EF=AE,
∵∠BEA+∠BAE=∠BEA+∠FEH=90°,
∴∠BAE=∠FEH,
在△AEB和△EFH中,
,
∴△AEB≌△EFH(AAS),
∴FH=BE,AB=EH,
∴EH=CB,
∴CH+CE=CE+BE,
∴CH=BE,
∴FH=CH,
∴∠FCH=45°,
∴∠BCG=45°,
∵∠CBG=90°,
∴△CBG是等腰直角三角形,
∴BG=BC=5;
故答案为:5;
(4)解:过点F作∠EFH=∠BEC,与ED的延长线交于点H,如图5,
∵四边形ABCD是菱形,
∴CB=CD,∠A=∠BCD=120°,
由旋转得∠BEF=120°,EF=BE,
∴∠BEC+∠CBE=∠BEC+∠FEH=60°,
∴∠CBE=∠FEH,
∴△BEC≌△EFH(AAS),
∴∠H=∠BCD=120°,EH=BC,FH=CE,
∴CD=EH,
∴DH=CE,
∴DH=FH,
∴∠FDH=∠DFH=30°,
∴∠CDG=30°,
∵∠DCG=180°﹣∠BCD=60°,
∴∠G=90°,
∴△DCG是直角三角形,
∵∠CDG=30°,
∴CG=CD=BC,
∵BG=6,
∴3CG=6,
∴CG=2.
故答案为:2.
20.(12分)在正方形ABCD中,AB=10,AC是对角线,点O是AC的中点,点E在AC上,连接DE,点C关于DE的对称点是C′,连接DC′,EC′.
(1)如图1,若DC′经过点O,求证:;
(2)如图2,连接CC′,BC′,若∠ADC′=2∠CBC′,求CC′的长;
(3)当点B,C′,E三点共线时,直接写出CE的长.
【解答】(1)证明:∵四边形ABCD是正方形,点O是对角线AC的中点,
∴OC′⊥AC,∠C′=∠ACD=45°,
∴△OEC′是等腰直角三角形.
由对称的性质得:CE=C′E,
∴;
(2)解:如图1,过点B作BN⊥CN交CC′的延长线于点N,延长DE交CC′于点M,
由对称的性质得:∠CDM=∠C′DM,DM⊥CC′,DC=DC′,CM=C′M
∴∠CDM+∠DCM=90°.
∵∠DCM+∠BCN=90°,
∴∠CDM=∠BCN.
∵BC=DC,∠N=∠DMC=90°,
∴△CDM≌△BCN(AAS),
∴BN=CM.
设则∠CBC′=α,∠ADC′=2α,
∴∠CDC′=90°﹣2α,
∴,
∴∠NC′B=∠C′CB+∠CBC′=45°,
∴△NC′B是等腰直角三角形,
∴C′N=BN,
∴BN=C′N=C′M=CM,
∴CN2+BN2=CB2=100,
∴(3BN)2+BN2=CB2=100,
∴,
∴.
(3)解:如图2,连接BD交AC于点H,则∠CDB=45°,,
当点E在CH上时,延长DE交CC′于点G,过点C′作FC′⊥BC于点F,连接AC′,则DG垂直平分CC′,
∴∠CDG+∠DCC′=90°,
∵∠C′CB+∠DCC′=90°,
∴∠C′CB=∠CDG,
在正方形ABCD中,CD=CB,∠BCE=∠DCE,∠ABC=∠BCD=90°,AD=BC,
∵CE=CE,
∴△BCE≌△DCE(SAS),
∴∠CBE=∠CDG,
∴∠C′CB=∠CBE,
∴∠DCC′=∠ABC′,
∴△DCC′≌△ABC′(SAS),
∴DC′=AC′,
由对称的性质得:DC′=DC,∠CDG=∠C′DG,
∴DC′=AC′=DC,
∴△AC′D是等边三角形,
∴∠ADC′=60°,
∴∠CDC′=30°,
∴∠CDG=∠C′DG=15°,
∴∠GDH=30°,
∴DE=2EH,
∵AB=AD=10,
∴,
∴,
∵EH2+DH2=DE2=2EH2,
∴,
∴,
∴CE=CH﹣EH=5﹣;
如图3,当点E在AH上时,
同理CE=5+;
综上所述,CE的长为5﹣或5+;
方法二:
如图4,
∵E在正方形的对角线上,
∴DC=BC,∠DCE=∠BCE,CE=CE,
∴△DEC≌△BEC(SAS),
∴∠1=∠2,
由折叠的性质得:∠1=∠DEC′,
∵∠1+∠2+∠DEC′=360°,
∴∠1=∠2=∠DEC′=120°,
∴∠OEB=60°,
作BO⊥AC交AC于点O,
∵BC=10,
∴BO=CO=5,
∴DE=cot60°×BO=°×5=,
∴CE=5﹣;
如图5,
同理得:∠1=∠2=∠3=60°,
解得:OE=,OC=OB=5,
∴CE=CO+OE=5+.
综上所述,CE的长为5﹣或5+.
一、选择题(本大题共8小题,每小题3分,共24分,每小题有四个选项,其中只有一个是正确的)
1.(3分)如图所示的几何体,其俯视图是( )
A. B.
C. D.
2.(3分)在传统游戏“石头、剪子、布”中,随机出一个手势,出“石头”的概率是( )
A. B. C. D.
3.(3分)不解方程,判断方程x2﹣4x﹣1=0的根的情况是( )
A.没有实数根 B.有两个相等实数根
C.有两个不相等实数根 D.无法确定
4.(3分)如图,在△ABC中,DE∥BC,,DE=4,则BC的长是( )
A.8 B.10 C.11 D.12
5.(3分)如图,张老汉想用长为70米的栅栏,再借助房屋的外墙(外墙足够长)围成一个面积为640平方米的矩形羊圈ABCD,并在边BC上留一个2米宽的门(建在EF处,门用其他材料),设AB的长为x米,则下面所列方程正确的是( )
A.x(70﹣x)=640 B.x(70﹣2x)=640
C.x(72﹣x)=640 D.x(72﹣2x)=640
6.(3分)如图,△ABC和△A1B1C1是以点P为位似中心的位似图形,若,△ABC的周长为6,则△A1B1C1的周长是( )
A.8 B.12 C.18 D.24
7.(3分)如图,在 ABCD中,点E,F分别在边AD和CD上,EF∥AC,连接BE交对角线AC于点G,若点G是AC的四等分点(AG<CG),AC=4,则EF的长为( )
A. B.2 C. D.3
8.(3分)在正方形ABCD中,AB=4,点E是边AD的中点,连接BE,将△ABE沿BE翻折,点A落在点F处,BF与AC交于点H,点O是AC的中点,则OH的长度是( )
A. B. C.4﹣2 D.
二、填空题(本题共5小题,每小题3分,共15分)
9.(3分)已知,则= .
10.(3分)在测量旗杆高度的活动课中,某小组学生于同一时刻在阳光下对一根直立于平地的竹竿及其影长和旗杆的影长进行了测量,得到的数据如图所示,根据这些数据计算出旗杆的高度为 m.
11.(3分)一个不透明的箱子里有3个球,其中2个白球,1个红球,它们除了颜色外其他都相同,从中任意摸出一个球,记下颜色后放回,搅匀,再摸出一个球,则摸出的两个球恰好颜色不同的概率为 .
12.(3分)如图,Rt△ABC中,∠ABC=90°,BD⊥AC,垂足为D,AE平分∠BAC,分别交BD,BC于点F,E.若AB:BC=3:4,则= .
13.(3分)在菱形ABCD中,E,F分别是AB,BC边上的中点,G为DE上一点,若AB=6,∠B=∠EGF=60°,则DG的长为 .
三、解答题(本题共7小题,其中第14题6分,第15题6分,第16题9分,第17题8分,第18题8分,第19题12分,第20题12分,共61分)
14.(6分)解一元二次方程:
(1)(x+2)2=3(x+2);
(2)x2﹣3x﹣1=0.
15.(6分)如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(1,﹣2)、B(4,﹣1),C(3,﹣3).
(1)画出将△ABC向左平移5个单位,再向上平移3个单位后的△A1B1C1;
(2)以原点O为位似中心,在位似中心的同侧画出△A1B1C1的一个位似△A2B2C2,使它与△A1B1C1的相似比为2:1;
(3)若△A1B1C1内部任意一点P1的坐标为(a,b),直接写出经过(2)的变化后点P1的对应点P2的坐标(用含a、b的代数式表示).
16.(9分)本期开学以来,初2015级开展了轰轰烈烈的体育锻炼,为了解考体育科目训练的效果,九年级学生中随机抽取了部分学生进行了以此中考体育科目测试(把测试结果分为四个等级,A等:优秀;B等:良好;C等:及格;D等:不及格),并将结果汇成了如图1、2所示两幅不同统计图,请根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 ;
(2)图1扇形图中D等所在的扇形的圆心角的度数是 ,并把图2条形统计图补充完整;
(3)我校九年级有1800名学生,如果全部参加这次中考体育科目测试,请估计不及格的人数为 ;
(4)已知得A等的同学有一位男生,体育老师想从4为同学中随机选择两位同学向其他同学介绍经验,请用列表法或画树形图的方法求出选中的两人刚好是一男一女的概率.
17.(8分)济南市公安交警部门提醒市民:“出门戴头盔,放心平安归”.某商店统计了某品牌头盔的销售量,四月份售出375个,六月份售出540个,且从四月份到六月份月增长率相同.
(1)求该品牌头盔销售量的月增长率;
(2)经市场调研发现,此种品牌头盔如果每个盈利10元,月销售量为500个,若在此基础上每个涨价1元,则月销售量将减少20个,现在既要使月销售利润达到6000元,又要尽可能让顾客得到实惠,那么该品牌头盔每个应涨价多少元?
18.(8分)如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E.
(1)求证:四边形ABCD是菱形;
(2)若,BD=2,求BE的长.
19.(12分)在数学综合与实践活动课上,同学们用两个完全相同的矩形纸片展开探究活动:
【实践探究】:(1)小红将两个矩形纸片摆成图1的形状,连接AG、AC,则∠ACG= °;
【解决问题】:(2)将矩形AQGF绕点A顺时针转动,边AF与边CD交于点M,连接BM,AB=10,AD=6.
①如图2,当BM=AB时,求证:AM平分∠DMB;写出证明过程
②如图3,当点F落在DC上时,连接BQ交AF于点O,则AO= ;
【迁移应用】:(3)如图4,正方形ABCD的边长为,E是BC边上一点(不与点B、C重合),连接AE,将线段AE绕点E顺时针旋转90°至FE,作射线FC交AB的延长线于点G,则BG= ;
(4)如图5,在菱形ABCD中,∠A=120°,E是CD边上一点(不与点C、D重合),连接BE,将线段BE绕点E顺时针旋转120°至FE,作射线FD交BC的延长线于点G,若,则CG= .
20.(12分)在正方形ABCD中,AB=10,AC是对角线,点O是AC的中点,点E在AC上,连接DE,点C关于DE的对称点是C′,连接DC′,EC′.
(1)如图1,若DC′经过点O,求证:;
(2)如图2,连接CC′,BC′,若∠ADC′=2∠CBC′,求CC′的长;
(3)当点B,C′,E三点共线时,直接写出CE的长.
2024-2025学年广东省深圳市福田外国语学校九年级(上)期中数学试卷
参考答案
一、选择题(本大题共8小题,每小题3分,共24分,每小题有四个选项,其中只有一个是正确的)
1.(3分)如图所示的几何体,其俯视图是( )
A. B.
C. D.
选:B.
2.(3分)在传统游戏“石头、剪子、布”中,随机出一个手势,出“石头”的概率是( )
A. B. C. D.
选:C.
3.(3分)不解方程,判断方程x2﹣4x﹣1=0的根的情况是( )
A.没有实数根 B.有两个相等实数根
C.有两个不相等实数根 D.无法确定
选:C.
4.(3分)如图,在△ABC中,DE∥BC,,DE=4,则BC的长是( )
A.8 B.10 C.11 D.12
选:D.
5.(3分)如图,张老汉想用长为70米的栅栏,再借助房屋的外墙(外墙足够长)围成一个面积为640平方米的矩形羊圈ABCD,并在边BC上留一个2米宽的门(建在EF处,门用其他材料),设AB的长为x米,则下面所列方程正确的是( )
A.x(70﹣x)=640 B.x(70﹣2x)=640
C.x(72﹣x)=640 D.x(72﹣2x)=640
选:D.
6.(3分)如图,△ABC和△A1B1C1是以点P为位似中心的位似图形,若,△ABC的周长为6,则△A1B1C1的周长是( )
A.8 B.12 C.18 D.24
选:B.
7.(3分)如图,在 ABCD中,点E,F分别在边AD和CD上,EF∥AC,连接BE交对角线AC于点G,若点G是AC的四等分点(AG<CG),AC=4,则EF的长为( )
A. B.2 C. D.3
选:C.
8.(3分)在正方形ABCD中,AB=4,点E是边AD的中点,连接BE,将△ABE沿BE翻折,点A落在点F处,BF与AC交于点H,点O是AC的中点,则OH的长度是( )
A. B. C.4﹣2 D.
选:A.
二、填空题(本题共5小题,每小题3分,共15分)
9.(3分)已知,则= ﹣ .
10.(3分)在测量旗杆高度的活动课中,某小组学生于同一时刻在阳光下对一根直立于平地的竹竿及其影长和旗杆的影长进行了测量,得到的数据如图所示,根据这些数据计算出旗杆的高度为 12 m.
11.(3分)一个不透明的箱子里有3个球,其中2个白球,1个红球,它们除了颜色外其他都相同,从中任意摸出一个球,记下颜色后放回,搅匀,再摸出一个球,则摸出的两个球恰好颜色不同的概率为 .
12.(3分)如图,Rt△ABC中,∠ABC=90°,BD⊥AC,垂足为D,AE平分∠BAC,分别交BD,BC于点F,E.若AB:BC=3:4,则= .
13.(3分)在菱形ABCD中,E,F分别是AB,BC边上的中点,G为DE上一点,若AB=6,∠B=∠EGF=60°,则DG的长为 .
三、解答题(本题共7小题,其中第14题6分,第15题6分,第16题9分,第17题8分,第18题8分,第19题12分,第20题12分,共61分)
14.(6分)解一元二次方程:
(1)(x+2)2=3(x+2);
(2)x2﹣3x﹣1=0.
【解答】解:(1)(x+2)2=3(x+2),
(x+2)2﹣3(x+2)=0,
(x+2﹣3)(x+2)=0,
x+2﹣3=0或x+2=0,
解得x1=1,x2=﹣2;
(2)x2﹣3x﹣1=0,
x2﹣3x=1,
x2﹣3x+=1+,
=1+,
=,
x﹣=,
解得x1=,x2=.
15.(6分)如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(1,﹣2)、B(4,﹣1),C(3,﹣3).
(1)画出将△ABC向左平移5个单位,再向上平移3个单位后的△A1B1C1;
(2)以原点O为位似中心,在位似中心的同侧画出△A1B1C1的一个位似△A2B2C2,使它与△A1B1C1的相似比为2:1;
(3)若△A1B1C1内部任意一点P1的坐标为(a,b),直接写出经过(2)的变化后点P1的对应点P2的坐标(用含a、b的代数式表示).
【解答】解:(1)如图所示,△A1B1C1为所求三角形.
(2)如图所示,△A2B2C2为所求角形.
(3)由题意可知△A2B2C2∽△A2B2C2,且相似比为2:1,
∴当点P1的坐标为(a,b)时,对应点P2的坐标为:(2a,2b).
16.(9分)本期开学以来,初2015级开展了轰轰烈烈的体育锻炼,为了解考体育科目训练的效果,九年级学生中随机抽取了部分学生进行了以此中考体育科目测试(把测试结果分为四个等级,A等:优秀;B等:良好;C等:及格;D等:不及格),并将结果汇成了如图1、2所示两幅不同统计图,请根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 25人 ;
(2)图1扇形图中D等所在的扇形的圆心角的度数是 43.2° ,并把图2条形统计图补充完整;
(3)我校九年级有1800名学生,如果全部参加这次中考体育科目测试,请估计不及格的人数为 216人 ;
(4)已知得A等的同学有一位男生,体育老师想从4为同学中随机选择两位同学向其他同学介绍经验,请用列表法或画树形图的方法求出选中的两人刚好是一男一女的概率.
【解答】解:(1)本次抽样测试的学生人数为10÷40%=25(人);
(2)D等级的人数为25﹣4﹣10﹣8=3,
所以D等所在的扇形的圆心角的度数=360°×=43.2°,
条形统计图补充为:
(3)1800×=216(人),
所以估计不及格的人数为216人;
故答案为25人,43.2°,216人;
(4)画树状图为:
共有12种等可能的结果数,其中选中的两人刚好是一男一女的结果数为6,
所以选中的两人刚好是一男一女的概率==.
17.(8分)济南市公安交警部门提醒市民:“出门戴头盔,放心平安归”.某商店统计了某品牌头盔的销售量,四月份售出375个,六月份售出540个,且从四月份到六月份月增长率相同.
(1)求该品牌头盔销售量的月增长率;
(2)经市场调研发现,此种品牌头盔如果每个盈利10元,月销售量为500个,若在此基础上每个涨价1元,则月销售量将减少20个,现在既要使月销售利润达到6000元,又要尽可能让顾客得到实惠,那么该品牌头盔每个应涨价多少元?
【解答】解:(1)设该品牌头盔销售量的月增长率x,
由题意得:375(1+x)2=540,
解得x1=0.2=20%,x2=﹣2.2(不合题意,舍去),
答:该品牌头盔销售量的月增长率为20%;
(2)设该品牌头盔每个应涨价m元,
由题意得:(10+m)(500﹣20m)=6000,
整理得:m2﹣15m+50=0,
解得m1=5,m2=10,
∵要尽可能让顾客得到实惠,
∴m=5,
答:该品牌的头盔每个应涨价5元.
18.(8分)如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E.
(1)求证:四边形ABCD是菱形;
(2)若,BD=2,求BE的长.
【解答】(1)证明:∵AB∥DC,
∴∠OAB=∠DCA,
∵AC平分∠DAB,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,则AD=CD,
又∵AB=AD,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AB=AD,
∴四边形ABCD是菱形.
(2)解:∵四边形ABCD是菱形,
∴,BD⊥AC,,,
由勾股定理可得:,
∵CE⊥AB,
在Rt△BCE中,CE2=BC2﹣BE2,
在Rt△ACE中,CE2=AC2﹣AE2=AC2﹣(AB+BE)2,
∴BC2﹣BE2=AC2﹣(AB+BE)2,即:,
解得:.
19.(12分)在数学综合与实践活动课上,同学们用两个完全相同的矩形纸片展开探究活动:
【实践探究】:(1)小红将两个矩形纸片摆成图1的形状,连接AG、AC,则∠ACG= 45 °;
【解决问题】:(2)将矩形AQGF绕点A顺时针转动,边AF与边CD交于点M,连接BM,AB=10,AD=6.
①如图2,当BM=AB时,求证:AM平分∠DMB;写出证明过程
②如图3,当点F落在DC上时,连接BQ交AF于点O,则AO= 4 ;
【迁移应用】:(3)如图4,正方形ABCD的边长为,E是BC边上一点(不与点B、C重合),连接AE,将线段AE绕点E顺时针旋转90°至FE,作射线FC交AB的延长线于点G,则BG= 5 ;
(4)如图5,在菱形ABCD中,∠A=120°,E是CD边上一点(不与点C、D重合),连接BE,将线段BE绕点E顺时针旋转120°至FE,作射线FD交BC的延长线于点G,若,则CG= 2 .
【解答】(1)解:∵长方形纸片ABCD和AFGQ是两个完全相同的长方形,
∴AC=AG,∠BAC=∠GAF,
∴∠BAC+∠CAD=∠GAF+∠CAD,
∴∠GAC=∠BAD=90°,
∴△ACG是等腰直角三角形,
∴∠ACG=45°,
故答案为:45;
(2)①证明:∵BM=AB,
∴∠BMA=∠BAM,
∵四边形ABCD是矩形,
∴AB∥DC,
∴∠DMA=∠MAB;
∴∠BMA=∠DMA,
∴AM平分∠DMB;
②解:过点B作BE⊥AF于点E,
∵AF=AB=10,AD=6,
∴DF==8,
∴CF=DC﹣DF=2,
∵AB=AF,
∴∠AFB=∠ABF,
∵AB∥CD,
∴∠ABF=∠CFB,
∴∠AFB=∠CFB,
∵BF=BF,∠C=∠BEF=90°,
∴△BCF≌△BEF(AAS),
∴CF=EF=2,BC=BE,
∴AE=8,
∵AD=AQ=BC,
∴AQ=BE,
∵∠QAO=∠BEO,∠AOQ=∠BOE,
∴△AOQ≌△EOB(AAS),
∴AO=OE=AE=4,
故答案为:4;
(3)解:如图4,过点F作FH⊥CD交CD于点H,
∵四边形ABCD是正方形,
∴CB=AB,∠ABC=90°,
∴∠H=∠ABC=90°,
由旋转的性质得:∠AEF=90°,EF=AE,
∵∠BEA+∠BAE=∠BEA+∠FEH=90°,
∴∠BAE=∠FEH,
在△AEB和△EFH中,
,
∴△AEB≌△EFH(AAS),
∴FH=BE,AB=EH,
∴EH=CB,
∴CH+CE=CE+BE,
∴CH=BE,
∴FH=CH,
∴∠FCH=45°,
∴∠BCG=45°,
∵∠CBG=90°,
∴△CBG是等腰直角三角形,
∴BG=BC=5;
故答案为:5;
(4)解:过点F作∠EFH=∠BEC,与ED的延长线交于点H,如图5,
∵四边形ABCD是菱形,
∴CB=CD,∠A=∠BCD=120°,
由旋转得∠BEF=120°,EF=BE,
∴∠BEC+∠CBE=∠BEC+∠FEH=60°,
∴∠CBE=∠FEH,
∴△BEC≌△EFH(AAS),
∴∠H=∠BCD=120°,EH=BC,FH=CE,
∴CD=EH,
∴DH=CE,
∴DH=FH,
∴∠FDH=∠DFH=30°,
∴∠CDG=30°,
∵∠DCG=180°﹣∠BCD=60°,
∴∠G=90°,
∴△DCG是直角三角形,
∵∠CDG=30°,
∴CG=CD=BC,
∵BG=6,
∴3CG=6,
∴CG=2.
故答案为:2.
20.(12分)在正方形ABCD中,AB=10,AC是对角线,点O是AC的中点,点E在AC上,连接DE,点C关于DE的对称点是C′,连接DC′,EC′.
(1)如图1,若DC′经过点O,求证:;
(2)如图2,连接CC′,BC′,若∠ADC′=2∠CBC′,求CC′的长;
(3)当点B,C′,E三点共线时,直接写出CE的长.
【解答】(1)证明:∵四边形ABCD是正方形,点O是对角线AC的中点,
∴OC′⊥AC,∠C′=∠ACD=45°,
∴△OEC′是等腰直角三角形.
由对称的性质得:CE=C′E,
∴;
(2)解:如图1,过点B作BN⊥CN交CC′的延长线于点N,延长DE交CC′于点M,
由对称的性质得:∠CDM=∠C′DM,DM⊥CC′,DC=DC′,CM=C′M
∴∠CDM+∠DCM=90°.
∵∠DCM+∠BCN=90°,
∴∠CDM=∠BCN.
∵BC=DC,∠N=∠DMC=90°,
∴△CDM≌△BCN(AAS),
∴BN=CM.
设则∠CBC′=α,∠ADC′=2α,
∴∠CDC′=90°﹣2α,
∴,
∴∠NC′B=∠C′CB+∠CBC′=45°,
∴△NC′B是等腰直角三角形,
∴C′N=BN,
∴BN=C′N=C′M=CM,
∴CN2+BN2=CB2=100,
∴(3BN)2+BN2=CB2=100,
∴,
∴.
(3)解:如图2,连接BD交AC于点H,则∠CDB=45°,,
当点E在CH上时,延长DE交CC′于点G,过点C′作FC′⊥BC于点F,连接AC′,则DG垂直平分CC′,
∴∠CDG+∠DCC′=90°,
∵∠C′CB+∠DCC′=90°,
∴∠C′CB=∠CDG,
在正方形ABCD中,CD=CB,∠BCE=∠DCE,∠ABC=∠BCD=90°,AD=BC,
∵CE=CE,
∴△BCE≌△DCE(SAS),
∴∠CBE=∠CDG,
∴∠C′CB=∠CBE,
∴∠DCC′=∠ABC′,
∴△DCC′≌△ABC′(SAS),
∴DC′=AC′,
由对称的性质得:DC′=DC,∠CDG=∠C′DG,
∴DC′=AC′=DC,
∴△AC′D是等边三角形,
∴∠ADC′=60°,
∴∠CDC′=30°,
∴∠CDG=∠C′DG=15°,
∴∠GDH=30°,
∴DE=2EH,
∵AB=AD=10,
∴,
∴,
∵EH2+DH2=DE2=2EH2,
∴,
∴,
∴CE=CH﹣EH=5﹣;
如图3,当点E在AH上时,
同理CE=5+;
综上所述,CE的长为5﹣或5+;
方法二:
如图4,
∵E在正方形的对角线上,
∴DC=BC,∠DCE=∠BCE,CE=CE,
∴△DEC≌△BEC(SAS),
∴∠1=∠2,
由折叠的性质得:∠1=∠DEC′,
∵∠1+∠2+∠DEC′=360°,
∴∠1=∠2=∠DEC′=120°,
∴∠OEB=60°,
作BO⊥AC交AC于点O,
∵BC=10,
∴BO=CO=5,
∴DE=cot60°×BO=°×5=,
∴CE=5﹣;
如图5,
同理得:∠1=∠2=∠3=60°,
解得:OE=,OC=OB=5,
∴CE=CO+OE=5+.
综上所述,CE的长为5﹣或5+.
同课章节目录
