广东省深圳市盐田区2024-2025学年九年级(上)期中数学试卷(含答案)
文档属性
| 名称 | 广东省深圳市盐田区2024-2025学年九年级(上)期中数学试卷(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 970.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-18 16:06:20 | ||
图片预览




文档简介
2024-2025学年广东省深圳市盐田区九年级(上)期中数学试卷
一、选择题(本大题有8小题,每小题3分,共24分)
1.(3分)隋朝时期的青瓷高足盘是湖北省博物馆重要馆藏文物之一,具有极高的历史价值、文化价值.如图所示,关于它的三视图,下列说法正确的是( )
A.主视图与左视图相同 B.主视图与俯视图相同
C.左视图与俯视图相同 D.三种视图都相同
2.(3分)关于x的一元二次方程x2+bx﹣10=0的一个根为2,则b的值为( )
A.﹣3 B.2 C.3 D.7
3.(3分)如图,在矩形ABCD中,对角线AC,BD交于点O.若∠AOB=50°,则∠ADB的度数为( )
A.65° B.50° C.25° D.20°
4.(3分)如图,带有刻度的直尺结合数轴作图,已知图中过点B和8的两条线段(两条线段的另一端在刻度尺上分别对应3和5)相互平行.若点A在数轴上表示的数是﹣2且点A与刻度尺上的0刻度重合,则AB的长度是( )
A.3 B.4 C.5 D.6
5.(3分)宽与长的比等于的矩形称为黄金矩形,黄金矩形给我们以协调、匀称的美感.世界上很多著名建筑,为了取得最佳的视觉效果,都采用了黄金矩形的设计,如古希腊的帕提侬庙等.如图,帕提侬神庙平面图的长约为30米,则它的宽约为( )
A.12.36米 B.18.54米 C.21.21米 D.48.54米
6.(3分)七巧板是一种拼图玩具,体现了我国古代劳动人民的智慧.如图,是一个由“七巧板”地砖铺成的地板,一个小球在该地板上自由地滚动,并随机停留在某块地砖上,已知小球停在任意一点的可能性都相同,那么小球停在4号地砖上的概率是( )
A. B. C. D.
7.(3分)如图,△ABC与△DEF是位似图形,点O是位似中心.若OA=2AD,△ABC的周长为4,则△DEF的周长为( )
A.6 B.8 C.9 D.12
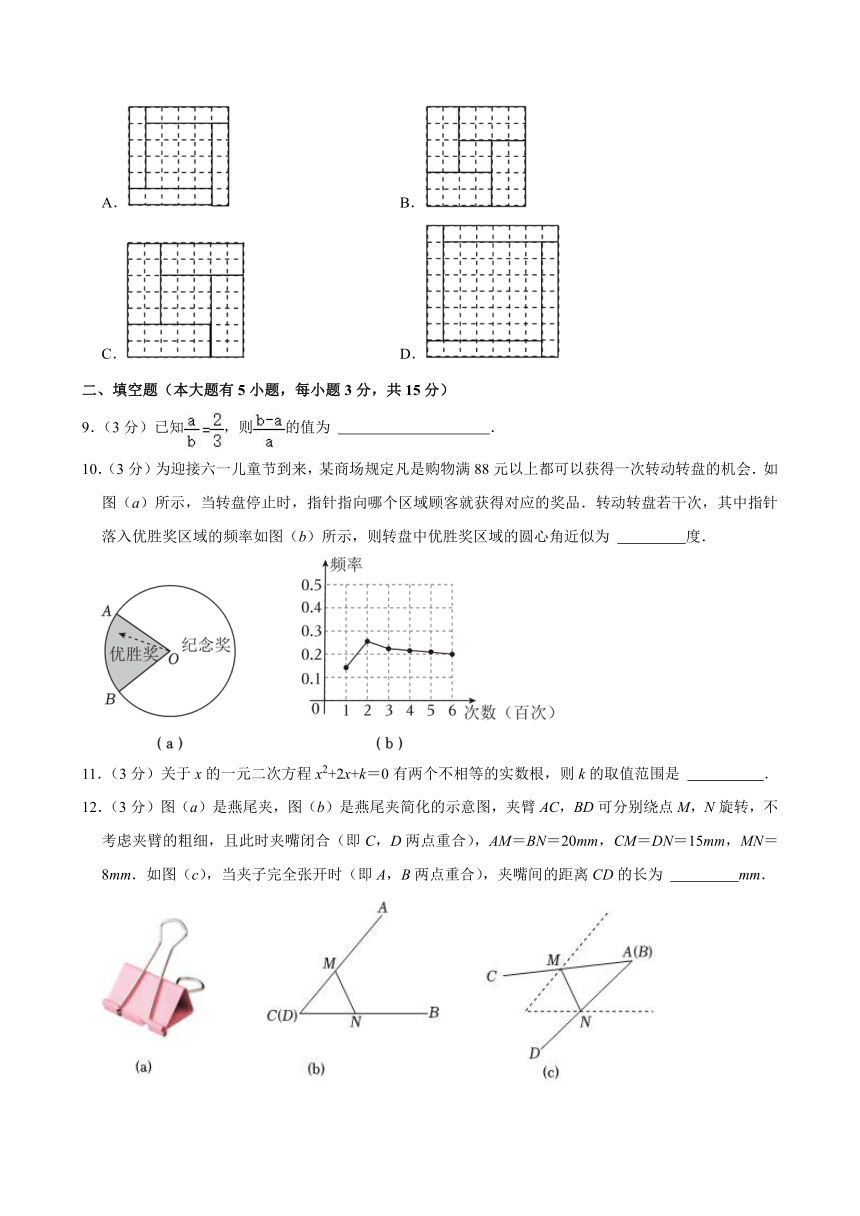
8.(3分)我国古代数学家赵爽(公元3~4世纪)在其所著的《勾股圆方图注》中记载过一元二次方程(正根)的几何解法.以方程x2+5x﹣14=0即x(x+5)=14为例说明,记载的方法是:构造如图面积是(x+x+5)2的大正方形.同时它又等于四个矩形的面积加上中间小正方形的面积,即4×14+52=81,因此x=2.则在下列四个构图中,能正确说明方程x2﹣3x﹣10=0解法的构图是( )
A. B.
C. D.
二、填空题(本大题有5小题,每小题3分,共15分)
9.(3分)已知,则的值为 .
10.(3分)为迎接六一儿童节到来,某商场规定凡是购物满88元以上都可以获得一次转动转盘的机会.如图(a)所示,当转盘停止时,指针指向哪个区域顾客就获得对应的奖品.转动转盘若干次,其中指针落入优胜奖区域的频率如图(b)所示,则转盘中优胜奖区域的圆心角近似为 度.
11.(3分)关于x的一元二次方程x2+2x+k=0有两个不相等的实数根,则k的取值范围是 .
12.(3分)图(a)是燕尾夹,图(b)是燕尾夹简化的示意图,夹臂AC,BD可分别绕点M,N旋转,不考虑夹臂的粗细,且此时夹嘴闭合(即C,D两点重合),AM=BN=20mm,CM=DN=15mm,MN=8mm.如图(c),当夹子完全张开时(即A,B两点重合),夹嘴间的距离CD的长为 mm.
13.(3分)如图,在正方形ABCD中,E是CD边上一点且满足∠CBE=30°,将△BCE沿BE折叠得到△BC′E,C′E与对角线BD交于点F,则的值为 .
三、解答题(本大题有7小题,共61分)
14.(6分)解一元二次方程:
(1)x2+2x=0;
(2)x2﹣6x﹣391=0.
15.(7分)化学实验课上,杨老师带来了Mg(镁)、Al(铝)、Zn(锌)、Cu(铜)四种金属材料及其元素卡片(如图,除正面信息不同外,其余均相同),将四张元素卡片背面朝上洗匀,让学生随机抽取一张,然后用抽取到的金属与盐酸反应来制取氢气.(根据金属活动顺序可知:Mg、Al、Zn可以置换出氢气,而Cu不能置换出氢气)
(1)小云随机从中抽取一张卡片,抽到“Al”的概率为 ;
(2)小云随机从中抽取一张卡片,记下金属后,放回洗匀,小南再从中随机抽取一张,请用列表或画树状图的方法求小云和小南抽到的金属均能置换出氢气的概率.
16.(8分)如图,在平行四边形ABCD中,∠BDC=90°,E是AD边上一点,延长BE与CD的延长线交于点F,连接AF.
(1)请从下列条件中选择一个能证明四边形ABDF是矩形的条件,并写出证明过程;
①AE=DE;②BF=BC;③AE=BE.
(2)若四边形ABDF是矩形,且AB=3,AD=5,求四边形ABCF的面积.
17.(8分)已知甲商品每件的进价为20元,售价为每件40元.
(1)若商场计划对甲商品降价促销,预备从原来售价的每件40元进行两次调价后将售价降为每件32.4元.若甲商品两次调价的降价率相同,求这个降价率;
(2)经调查,甲商品每降价1元时,每月可多销售10件.已知甲商品在原售价为每件40元时的月销售量为100件.若商场希望甲商品该月的获利为2250元,请问甲商品在原售价的基础上应降价多少元?
18.(10分)综合与实践
背景 晚上小明在广场上散步,如图(a)所示,AB,CD是广场上的两根电线杆,小明站在点E处,在两盏路灯B,D的照射下,地面上形成了他的两个影子EH,EG.
素材1 两盏路灯B,D的高均为10m,两盏路灯相距40m,小明的身高EF为1.5m.
素材2 A,C,E,G,H在同一平面内,电线杆和人均垂直于地面.
问题提出 小明在广场中走动时(始终保证影子EG,EH不为0),两个影子端点间的距离GH是否会发生改变?
问题解决
任务1 计算 (1)如图(b),当小明影子EG长为4.5m时,此时小明到电线杆CD的距离EC为多少?
任务2 说理 (2)小明在广场上走动的过程中两个影子端点间的距离GH是否会改变?若GH的长不变,请求出GH的长;若GH的长度发生变化,请说明理由.
任务3 拓展 (3)小明在广场的某个位置向上跳起再落下,在该过程中GH最长达到10m,请直接写出小明从起跳到落下的过程中,头顶距离地面的最大高度.
19.(11分)综合与探究
【定义】我们把关于x的一元二次方程ax2+bx+c=0与cx2+bx+a=0(ac≠0,a≠c)称为一对“友好方程”.
【示例】如2x2+7x﹣3=0的“友好方程”是﹣3x2+7x+2=0.
(1)写出一元二次方程12x2﹣7x+1=0的“友好方程”是 .
【探究】
(2)已知一元二次方程12x2﹣7x+1=0的两根为,,请求出它的“友好方程”的两个根.
【猜想】.
(3)当Δ=b2﹣4ac≥0时,方程ax2+bx+c=0的两根x1,x2与其“友好方程”cx2+bx+a=0的两根x3,x4之间存在的一种特殊关系为 .(ac≠0,a≠c)
【证明】
∵方程ax2+bx+c=0的两根为,;
方程cx2+bx+a=0的两根为,① ;
…
(4)请完成上述填空①,并补全证明过程.(备注:证明一组关系即可)
【拓展】
(5)已知关于x的方程2024x2+bx﹣c=0的两根是x1=﹣1,,请利用上述结论,直接写出关于x的方程c(x﹣1)2﹣bx+b=2024的两根.
20.(11分)综合与探究
如图,在平行四边形ABCD中,E,F分别是边BC,CD上的点,AE与BF交于点P.
(1)【特例感知】
如图(a),若四边形ABCD是正方形,当∠APB=∠D时,则线段AE与BF的数量关系是 ;
(2)【深入探究】
如图(b),若四边形ABCD是菱形,且∠APB=∠D,则线段AE与BF满足怎样的数量关系?请证明你的猜想;关于此问,数学兴趣小组给出如下两种解决思路.请选择其中一种思路解决问题.
思路一 思路二
如图,在BC边上取一点M使AM=AB,… 如图,在CB的延长线上取一点N使AN=AE,…
(3)【类比迁移】
如图(c),若四边形ABCD是菱形,E为BC的中点,∠APB=∠C=60°,请求出的值;
(4)【联系拓广】
如图(d),在平行四边形ABCD中,AD=3,AB=4,∠C=60°,F是CD边的中点,当点E在直线BC上运动,且直线AE与直线BF所夹的锐角为60°时,请直接写BE的长.
2024-2025学年广东省深圳市盐田区九年级(上)期中数学试卷
参考答案
一、选择题(本大题有8小题,每小题3分,共24分)
1.(3分)隋朝时期的青瓷高足盘是湖北省博物馆重要馆藏文物之一,具有极高的历史价值、文化价值.如图所示,关于它的三视图,下列说法正确的是( )
A.主视图与左视图相同 B.主视图与俯视图相同
C.左视图与俯视图相同 D.三种视图都相同
选:A.
2.(3分)关于x的一元二次方程x2+bx﹣10=0的一个根为2,则b的值为( )
A.﹣3 B.2 C.3 D.7
选:C.
3.(3分)如图,在矩形ABCD中,对角线AC,BD交于点O.若∠AOB=50°,则∠ADB的度数为( )
A.65° B.50° C.25° D.20°
选:C.
4.(3分)如图,带有刻度的直尺结合数轴作图,已知图中过点B和8的两条线段(两条线段的另一端在刻度尺上分别对应3和5)相互平行.若点A在数轴上表示的数是﹣2且点A与刻度尺上的0刻度重合,则AB的长度是( )
A.3 B.4 C.5 D.6
选:D.
5.(3分)宽与长的比等于的矩形称为黄金矩形,黄金矩形给我们以协调、匀称的美感.世界上很多著名建筑,为了取得最佳的视觉效果,都采用了黄金矩形的设计,如古希腊的帕提侬庙等.如图,帕提侬神庙平面图的长约为30米,则它的宽约为( )
A.12.36米 B.18.54米 C.21.21米 D.48.54米
选:B.
6.(3分)七巧板是一种拼图玩具,体现了我国古代劳动人民的智慧.如图,是一个由“七巧板”地砖铺成的地板,一个小球在该地板上自由地滚动,并随机停留在某块地砖上,已知小球停在任意一点的可能性都相同,那么小球停在4号地砖上的概率是( )
A. B. C. D.
选:D.
7.(3分)如图,△ABC与△DEF是位似图形,点O是位似中心.若OA=2AD,△ABC的周长为4,则△DEF的周长为( )
A.6 B.8 C.9 D.12
选:A.
8.(3分)我国古代数学家赵爽(公元3~4世纪)在其所著的《勾股圆方图注》中记载过一元二次方程(正根)的几何解法.以方程x2+5x﹣14=0即x(x+5)=14为例说明,记载的方法是:构造如图面积是(x+x+5)2的大正方形.同时它又等于四个矩形的面积加上中间小正方形的面积,即4×14+52=81,因此x=2.则在下列四个构图中,能正确说明方程x2﹣3x﹣10=0解法的构图是( )
A. B.
C. D.
选:C.
二、填空题(本大题有5小题,每小题3分,共15分)
9.(3分)已知,则的值为 .
10.(3分)为迎接六一儿童节到来,某商场规定凡是购物满88元以上都可以获得一次转动转盘的机会.如图(a)所示,当转盘停止时,指针指向哪个区域顾客就获得对应的奖品.转动转盘若干次,其中指针落入优胜奖区域的频率如图(b)所示,则转盘中优胜奖区域的圆心角近似为 72 度.
11.(3分)关于x的一元二次方程x2+2x+k=0有两个不相等的实数根,则k的取值范围是 k<1 .
12.(3分)图(a)是燕尾夹,图(b)是燕尾夹简化的示意图,夹臂AC,BD可分别绕点M,N旋转,不考虑夹臂的粗细,且此时夹嘴闭合(即C,D两点重合),AM=BN=20mm,CM=DN=15mm,MN=8mm.如图(c),当夹子完全张开时(即A,B两点重合),夹嘴间的距离CD的长为 14 mm.
13.(3分)如图,在正方形ABCD中,E是CD边上一点且满足∠CBE=30°,将△BCE沿BE折叠得到△BC′E,C′E与对角线BD交于点F,则的值为 .
三、解答题(本大题有7小题,共61分)
14.(6分)解一元二次方程:
(1)x2+2x=0;
(2)x2﹣6x﹣391=0.
【解答】解:(1)x2+2x=0,
x(x+2)=0,
∴x=0或x+2=0,
∴x1=0,x2=﹣2;
(2)x2﹣6x﹣391=0,
x2﹣6x=391,
x2﹣6x+9=391+9,即(x﹣3)2=400,
∴x﹣3=±20,
∴x1=23,x2=﹣17.
15.(7分)化学实验课上,杨老师带来了Mg(镁)、Al(铝)、Zn(锌)、Cu(铜)四种金属材料及其元素卡片(如图,除正面信息不同外,其余均相同),将四张元素卡片背面朝上洗匀,让学生随机抽取一张,然后用抽取到的金属与盐酸反应来制取氢气.(根据金属活动顺序可知:Mg、Al、Zn可以置换出氢气,而Cu不能置换出氢气)
(1)小云随机从中抽取一张卡片,抽到“Al”的概率为 ;
(2)小云随机从中抽取一张卡片,记下金属后,放回洗匀,小南再从中随机抽取一张,请用列表或画树状图的方法求小云和小南抽到的金属均能置换出氢气的概率.
【解答】解:(1)由题意知,共有4种等可能的结果,其中抽到“Al”的结果有1种,
∴小云随机从中抽取一张卡片,抽到“Al”的概率为.
故答案为:.
(2)列表如下:
Mg Al Zn Cu
Mg (Mg,Mg) (Mg,Al) (Mg,Zn) (Mg,Cu)
Al (Al,Mg) (Al,Al) (Al,Zn) (Al,Cu)
Zn (Zn,Mg) (Zn,Al) (Zn,Zn) (Zn,Cu)
Cu (Cu,Mg) (Cu,Al) (Cu,Zn) (Cu,Cu)
共有16种等可能的结果,其中小云和小南抽到的金属均能置换出氢气的结果有:(Mg,Mg),(Mg,Al),(Mg,Zn),(Al,Mg),(Al,Al),(Al,Zn),(Zn,Mg),(Zn,Al),(Zn,Zn),共9种,
∴小云和小南抽到的金属均能置换出氢气的概率为.
16.(8分)如图,在平行四边形ABCD中,∠BDC=90°,E是AD边上一点,延长BE与CD的延长线交于点F,连接AF.
(1)请从下列条件中选择一个能证明四边形ABDF是矩形的条件,并写出证明过程;
①AE=DE;②BF=BC;③AE=BE.
(2)若四边形ABDF是矩形,且AB=3,AD=5,求四边形ABCF的面积.
【解答】解:(1)选①AE=DE.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABE=∠DFE,
在△ABE和△DFE中,
,
∴△ABE≌△DFE(AAS),
∴AB=DF,
∵AB∥DF,AB=DF,
∴四边形ABDF是平行四边形,
∵∠BDC=90°,
∴∠BDF=90°,
∴四边形ABDF是矩形;
(2)解:∵四边形ABDF是矩形,
∴AB=DF,
∵四边形ABDF是平行四边形,
∴AB=CD,
∴AB=DF=CD=3,
∴CF=DF+CD=3+3=6,
在Rt△BDC中,BC=AD=5,CD=3,
∴BD===4,
∵AB∥CF,
∴S=BD(AB+CF)=×4×(3+6)=18,
∴四边形ABCF的面积S等于18.
17.(8分)已知甲商品每件的进价为20元,售价为每件40元.
(1)若商场计划对甲商品降价促销,预备从原来售价的每件40元进行两次调价后将售价降为每件32.4元.若甲商品两次调价的降价率相同,求这个降价率;
(2)经调查,甲商品每降价1元时,每月可多销售10件.已知甲商品在原售价为每件40元时的月销售量为100件.若商场希望甲商品该月的获利为2250元,请问甲商品在原售价的基础上应降价多少元?
【解答】解:(1)设这个降价率为x,
依题意得:40(1﹣x)2=32.4,
解得:x1=0.1=10%,x2=1.9(不符合题意,舍去),
答:这个降价率为10%;
(2)设甲商品在原售价的基础上应降价y元,则每月销售量为(100+10x)件,
依题意得:(40﹣20﹣y)(100+10y)=2250,
整理得:y2﹣10y+25=0,
解得:y1=y2=5,
答:甲商品在原售价的基础上应降价5元.
18.(10分)综合与实践
背景 晚上小明在广场上散步,如图(a)所示,AB,CD是广场上的两根电线杆,小明站在点E处,在两盏路灯B,D的照射下,地面上形成了他的两个影子EH,EG.
素材1 两盏路灯B,D的高均为10m,两盏路灯相距40m,小明的身高EF为1.5m.
素材2 A,C,E,G,H在同一平面内,电线杆和人均垂直于地面.
问题提出 小明在广场中走动时(始终保证影子EG,EH不为0),两个影子端点间的距离GH是否会发生改变?
问题解决
任务1 计算 (1)如图(b),当小明影子EG长为4.5m时,此时小明到电线杆CD的距离EC为多少?
任务2 说理 (2)小明在广场上走动的过程中两个影子端点间的距离GH是否会改变?若GH的长不变,请求出GH的长;若GH的长度发生变化,请说明理由.
任务3 拓展 (3)小明在广场的某个位置向上跳起再落下,在该过程中GH最长达到10m,请直接写出小明从起跳到落下的过程中,头顶距离地面的最大高度.
【解答】解:(1)根据题意,EF∥AB∥CD,AB=CD.
∴=,
∴===.
当EG=4.5m时,CE==25.5m.
故小明到电线杆CD的距离EC为25.5m.
(2)由(1)得==.
又∵∠HEG=∠AEC,
∴△HEG∽△AEC,
∴.
又∵AC=40m,
∴GH=AC =m.
故GH的长度不会改变,GH=m.
(3)由(2)可知.
∴GH==.
当小明跳起时,EF变大,(﹣1)变小,GH变大,当小明跳到最高点时,GH最大长度为10m.
∴10=.
解得EF=2m.
故从起跳到落下的过程中,头顶距离地面的最大高度为2m.
19.(11分)综合与探究
【定义】我们把关于x的一元二次方程ax2+bx+c=0与cx2+bx+a=0(ac≠0,a≠c)称为一对“友好方程”.
【示例】如2x2+7x﹣3=0的“友好方程”是﹣3x2+7x+2=0.
(1)写出一元二次方程12x2﹣7x+1=0的“友好方程”是 x2﹣7x+12=0 .
【探究】
(2)已知一元二次方程12x2﹣7x+1=0的两根为,,请求出它的“友好方程”的两个根.
【猜想】.
(3)当Δ=b2﹣4ac≥0时,方程ax2+bx+c=0的两根x1,x2与其“友好方程”cx2+bx+a=0的两根x3,x4之间存在的一种特殊关系为 互为倒数 .(ac≠0,a≠c)
【证明】
∵方程ax2+bx+c=0的两根为,;
方程cx2+bx+a=0的两根为,① x4= ;
…
(4)请完成上述填空①,并补全证明过程.(备注:证明一组关系即可)
【拓展】
(5)已知关于x的方程2024x2+bx﹣c=0的两根是x1=﹣1,,请利用上述结论,直接写出关于x的方程c(x﹣1)2﹣bx+b=2024的两根.
【解答】解:(1)一元二次方程12x2﹣7x+1=0的“友好方程”为:x2﹣7x+12=0,
故答案为:x2﹣7x+12=0;
(2)x2﹣7x+12=0,
(x﹣3)(x﹣4)=0,
解得x1=3,x2=4;
(3)根据(2)的结论,猜想当Δ=b2﹣4ac≥0时,ax2+bx+c=0的两根x1、x2与其“友好方程”cx2+bx+a=0的两根x3、x4之间存在的一种特殊关系为互为倒数,(ac≠0,a≠c),
故答案为:互为倒数;
(4)证明如下:
∵方程ax2+bx+c=0的两根为,;
“友好方程”cx2+bx+a=0的两根为,x4=,
∴x1 x4= ===1,x2 x3= ===1,
即原方程的两根与“友好方程”的两根互为倒数,
故答案为:x4=;
(5)关于x的方程2024x2+bx﹣c=0的两根是x1=﹣1,,
∴该方程的“友好方程”﹣cx2+bx+2024=0,即cx2﹣bx﹣2024=0的两根为x1=﹣1,x2=2024,
则c(x﹣1)2﹣bx+b=2024,即c(x﹣1)2﹣b(x﹣1)﹣2024=0中x﹣1=﹣1或x﹣1=2024,
∴该方程的解为x1=0,x2=2025.
20.(11分)综合与探究
如图,在平行四边形ABCD中,E,F分别是边BC,CD上的点,AE与BF交于点P.
(1)【特例感知】
如图(a),若四边形ABCD是正方形,当∠APB=∠D时,则线段AE与BF的数量关系是 AE=BF ;
(2)【深入探究】
如图(b),若四边形ABCD是菱形,且∠APB=∠D,则线段AE与BF满足怎样的数量关系?请证明你的猜想;关于此问,数学兴趣小组给出如下两种解决思路.请选择其中一种思路解决问题.
思路一 思路二
如图,在BC边上取一点M使AM=AB,… 如图,在CB的延长线上取一点N使AN=AE,…
(3)【类比迁移】
如图(c),若四边形ABCD是菱形,E为BC的中点,∠APB=∠C=60°,请求出的值;
(4)【联系拓广】
如图(d),在平行四边形ABCD中,AD=3,AB=4,∠C=60°,F是CD边的中点,当点E在直线BC上运动,且直线AE与直线BF所夹的锐角为60°时,请直接写BE的长.
【解答】解:(1)当四边形ABCD是正方形,∠APB=∠D=90°.
∴∠BAP+∠ABP=∠BAP+∠EBP=90°.
∴∠ABP=∠EBP.
又∵AB=BC,∠ABC=∠C.
∴△ABE≌△BCF(ASA).
∴AE=BF.
故答案为:AE=BF.
(2)猜想AE=BF.
证明:
思路一:如图,在BC上取一点M,使AB=AM,则∠ABM=∠AMB.
∵四边形ABCD是菱形.
∴AB∥CD,AB=BC=AM,∠ABM+∠C=180°,∠D=∠ABE.
∵∠AME+∠AMB=180°,∠ABM+∠C=180°,
∴∠AME=∠C.
∵∠APB=∠D=∠ABM=∠AMB=60°,
∴∠FBC=∠APB﹣∠AEM=∠AMB﹣∠AEM=∠EAM.
在△AEM和△BFC中,∠FBC=∠EAM,AM=BC,∠AME=∠C,
∴△AEM≌△BFC(ASA).
∴AE=BF.
思路二:如图,在CB延长线上取点N,使AN=AE,则∠ANB=∠AEB.
根据菱形的性质∠ABC+∠C=180°,
∴∠ABN=∠C.
又∵∠BAN=∠ABC﹣∠ANB,∠APB﹣∠AEB=∠CBF,
∴∠BAN=∠CBF.
在△ABN和△BCF中,∠BAN=∠CBF,AB=BC,∠ABN=∠C,
∴△ABN≌△BCF(AAS).
∴AN=BF,
∴AE=BF.
(3)如图,延长AB,使BG=BE.
∵AB∥CD,
∴∠BGC=∠C=60°,
∴△BGE是等边三角形.
∴∠G=60°,BG=BE=BC=AB.
∵∠BAE+∠BEA=∠BGC,∠PBE+∠BEP=∠APB,∠APB=∠C=60°,
∴∠BAE=∠PBE.
在△EAG和△FBC中,∠GAE=∠CBF,∠G=∠C,
∴△EAG∽△FBC.
∴===.
(4)如图,AE、AE′分别与直线BF相交于G、I,∠AIB=∠AGB=60°.
∴△AGI为等边三角形.
过点F作FJ⊥BC,垂足为J,则JC=FC cosC=,FJ=FC sinC=FC.
又∵FC==2,
∴JC=1,FJ=,BJ=BC﹣JC=2,BF==.
∵AB∥CD,
∴∠ABI=∠BFC,
又∵∠AIB=∠C=60°
∴△ABI∽△BFC.
∴.即,
∴AI=,BI=
∴AG=GI=AI=,GB=GI﹣BI=.
在△BAE和△GAB中,∠BAE=∠GAB,∠AGB=∠ABE=60°,
∴△BAE∽△GAB.
∴=,
∴BE=,AE=.
在△GAB和△AE′E中,∠GAB=60°﹣∠E′AB=∠AE′E,∠E′AE=∠AGB=60°,
∴△GAB∽△AE′E.
∴,则E′E=,
∴BE′=E′E﹣BE=8.
故BE的长度为或8.
一、选择题(本大题有8小题,每小题3分,共24分)
1.(3分)隋朝时期的青瓷高足盘是湖北省博物馆重要馆藏文物之一,具有极高的历史价值、文化价值.如图所示,关于它的三视图,下列说法正确的是( )
A.主视图与左视图相同 B.主视图与俯视图相同
C.左视图与俯视图相同 D.三种视图都相同
2.(3分)关于x的一元二次方程x2+bx﹣10=0的一个根为2,则b的值为( )
A.﹣3 B.2 C.3 D.7
3.(3分)如图,在矩形ABCD中,对角线AC,BD交于点O.若∠AOB=50°,则∠ADB的度数为( )
A.65° B.50° C.25° D.20°
4.(3分)如图,带有刻度的直尺结合数轴作图,已知图中过点B和8的两条线段(两条线段的另一端在刻度尺上分别对应3和5)相互平行.若点A在数轴上表示的数是﹣2且点A与刻度尺上的0刻度重合,则AB的长度是( )
A.3 B.4 C.5 D.6
5.(3分)宽与长的比等于的矩形称为黄金矩形,黄金矩形给我们以协调、匀称的美感.世界上很多著名建筑,为了取得最佳的视觉效果,都采用了黄金矩形的设计,如古希腊的帕提侬庙等.如图,帕提侬神庙平面图的长约为30米,则它的宽约为( )
A.12.36米 B.18.54米 C.21.21米 D.48.54米
6.(3分)七巧板是一种拼图玩具,体现了我国古代劳动人民的智慧.如图,是一个由“七巧板”地砖铺成的地板,一个小球在该地板上自由地滚动,并随机停留在某块地砖上,已知小球停在任意一点的可能性都相同,那么小球停在4号地砖上的概率是( )
A. B. C. D.
7.(3分)如图,△ABC与△DEF是位似图形,点O是位似中心.若OA=2AD,△ABC的周长为4,则△DEF的周长为( )
A.6 B.8 C.9 D.12
8.(3分)我国古代数学家赵爽(公元3~4世纪)在其所著的《勾股圆方图注》中记载过一元二次方程(正根)的几何解法.以方程x2+5x﹣14=0即x(x+5)=14为例说明,记载的方法是:构造如图面积是(x+x+5)2的大正方形.同时它又等于四个矩形的面积加上中间小正方形的面积,即4×14+52=81,因此x=2.则在下列四个构图中,能正确说明方程x2﹣3x﹣10=0解法的构图是( )
A. B.
C. D.
二、填空题(本大题有5小题,每小题3分,共15分)
9.(3分)已知,则的值为 .
10.(3分)为迎接六一儿童节到来,某商场规定凡是购物满88元以上都可以获得一次转动转盘的机会.如图(a)所示,当转盘停止时,指针指向哪个区域顾客就获得对应的奖品.转动转盘若干次,其中指针落入优胜奖区域的频率如图(b)所示,则转盘中优胜奖区域的圆心角近似为 度.
11.(3分)关于x的一元二次方程x2+2x+k=0有两个不相等的实数根,则k的取值范围是 .
12.(3分)图(a)是燕尾夹,图(b)是燕尾夹简化的示意图,夹臂AC,BD可分别绕点M,N旋转,不考虑夹臂的粗细,且此时夹嘴闭合(即C,D两点重合),AM=BN=20mm,CM=DN=15mm,MN=8mm.如图(c),当夹子完全张开时(即A,B两点重合),夹嘴间的距离CD的长为 mm.
13.(3分)如图,在正方形ABCD中,E是CD边上一点且满足∠CBE=30°,将△BCE沿BE折叠得到△BC′E,C′E与对角线BD交于点F,则的值为 .
三、解答题(本大题有7小题,共61分)
14.(6分)解一元二次方程:
(1)x2+2x=0;
(2)x2﹣6x﹣391=0.
15.(7分)化学实验课上,杨老师带来了Mg(镁)、Al(铝)、Zn(锌)、Cu(铜)四种金属材料及其元素卡片(如图,除正面信息不同外,其余均相同),将四张元素卡片背面朝上洗匀,让学生随机抽取一张,然后用抽取到的金属与盐酸反应来制取氢气.(根据金属活动顺序可知:Mg、Al、Zn可以置换出氢气,而Cu不能置换出氢气)
(1)小云随机从中抽取一张卡片,抽到“Al”的概率为 ;
(2)小云随机从中抽取一张卡片,记下金属后,放回洗匀,小南再从中随机抽取一张,请用列表或画树状图的方法求小云和小南抽到的金属均能置换出氢气的概率.
16.(8分)如图,在平行四边形ABCD中,∠BDC=90°,E是AD边上一点,延长BE与CD的延长线交于点F,连接AF.
(1)请从下列条件中选择一个能证明四边形ABDF是矩形的条件,并写出证明过程;
①AE=DE;②BF=BC;③AE=BE.
(2)若四边形ABDF是矩形,且AB=3,AD=5,求四边形ABCF的面积.
17.(8分)已知甲商品每件的进价为20元,售价为每件40元.
(1)若商场计划对甲商品降价促销,预备从原来售价的每件40元进行两次调价后将售价降为每件32.4元.若甲商品两次调价的降价率相同,求这个降价率;
(2)经调查,甲商品每降价1元时,每月可多销售10件.已知甲商品在原售价为每件40元时的月销售量为100件.若商场希望甲商品该月的获利为2250元,请问甲商品在原售价的基础上应降价多少元?
18.(10分)综合与实践
背景 晚上小明在广场上散步,如图(a)所示,AB,CD是广场上的两根电线杆,小明站在点E处,在两盏路灯B,D的照射下,地面上形成了他的两个影子EH,EG.
素材1 两盏路灯B,D的高均为10m,两盏路灯相距40m,小明的身高EF为1.5m.
素材2 A,C,E,G,H在同一平面内,电线杆和人均垂直于地面.
问题提出 小明在广场中走动时(始终保证影子EG,EH不为0),两个影子端点间的距离GH是否会发生改变?
问题解决
任务1 计算 (1)如图(b),当小明影子EG长为4.5m时,此时小明到电线杆CD的距离EC为多少?
任务2 说理 (2)小明在广场上走动的过程中两个影子端点间的距离GH是否会改变?若GH的长不变,请求出GH的长;若GH的长度发生变化,请说明理由.
任务3 拓展 (3)小明在广场的某个位置向上跳起再落下,在该过程中GH最长达到10m,请直接写出小明从起跳到落下的过程中,头顶距离地面的最大高度.
19.(11分)综合与探究
【定义】我们把关于x的一元二次方程ax2+bx+c=0与cx2+bx+a=0(ac≠0,a≠c)称为一对“友好方程”.
【示例】如2x2+7x﹣3=0的“友好方程”是﹣3x2+7x+2=0.
(1)写出一元二次方程12x2﹣7x+1=0的“友好方程”是 .
【探究】
(2)已知一元二次方程12x2﹣7x+1=0的两根为,,请求出它的“友好方程”的两个根.
【猜想】.
(3)当Δ=b2﹣4ac≥0时,方程ax2+bx+c=0的两根x1,x2与其“友好方程”cx2+bx+a=0的两根x3,x4之间存在的一种特殊关系为 .(ac≠0,a≠c)
【证明】
∵方程ax2+bx+c=0的两根为,;
方程cx2+bx+a=0的两根为,① ;
…
(4)请完成上述填空①,并补全证明过程.(备注:证明一组关系即可)
【拓展】
(5)已知关于x的方程2024x2+bx﹣c=0的两根是x1=﹣1,,请利用上述结论,直接写出关于x的方程c(x﹣1)2﹣bx+b=2024的两根.
20.(11分)综合与探究
如图,在平行四边形ABCD中,E,F分别是边BC,CD上的点,AE与BF交于点P.
(1)【特例感知】
如图(a),若四边形ABCD是正方形,当∠APB=∠D时,则线段AE与BF的数量关系是 ;
(2)【深入探究】
如图(b),若四边形ABCD是菱形,且∠APB=∠D,则线段AE与BF满足怎样的数量关系?请证明你的猜想;关于此问,数学兴趣小组给出如下两种解决思路.请选择其中一种思路解决问题.
思路一 思路二
如图,在BC边上取一点M使AM=AB,… 如图,在CB的延长线上取一点N使AN=AE,…
(3)【类比迁移】
如图(c),若四边形ABCD是菱形,E为BC的中点,∠APB=∠C=60°,请求出的值;
(4)【联系拓广】
如图(d),在平行四边形ABCD中,AD=3,AB=4,∠C=60°,F是CD边的中点,当点E在直线BC上运动,且直线AE与直线BF所夹的锐角为60°时,请直接写BE的长.
2024-2025学年广东省深圳市盐田区九年级(上)期中数学试卷
参考答案
一、选择题(本大题有8小题,每小题3分,共24分)
1.(3分)隋朝时期的青瓷高足盘是湖北省博物馆重要馆藏文物之一,具有极高的历史价值、文化价值.如图所示,关于它的三视图,下列说法正确的是( )
A.主视图与左视图相同 B.主视图与俯视图相同
C.左视图与俯视图相同 D.三种视图都相同
选:A.
2.(3分)关于x的一元二次方程x2+bx﹣10=0的一个根为2,则b的值为( )
A.﹣3 B.2 C.3 D.7
选:C.
3.(3分)如图,在矩形ABCD中,对角线AC,BD交于点O.若∠AOB=50°,则∠ADB的度数为( )
A.65° B.50° C.25° D.20°
选:C.
4.(3分)如图,带有刻度的直尺结合数轴作图,已知图中过点B和8的两条线段(两条线段的另一端在刻度尺上分别对应3和5)相互平行.若点A在数轴上表示的数是﹣2且点A与刻度尺上的0刻度重合,则AB的长度是( )
A.3 B.4 C.5 D.6
选:D.
5.(3分)宽与长的比等于的矩形称为黄金矩形,黄金矩形给我们以协调、匀称的美感.世界上很多著名建筑,为了取得最佳的视觉效果,都采用了黄金矩形的设计,如古希腊的帕提侬庙等.如图,帕提侬神庙平面图的长约为30米,则它的宽约为( )
A.12.36米 B.18.54米 C.21.21米 D.48.54米
选:B.
6.(3分)七巧板是一种拼图玩具,体现了我国古代劳动人民的智慧.如图,是一个由“七巧板”地砖铺成的地板,一个小球在该地板上自由地滚动,并随机停留在某块地砖上,已知小球停在任意一点的可能性都相同,那么小球停在4号地砖上的概率是( )
A. B. C. D.
选:D.
7.(3分)如图,△ABC与△DEF是位似图形,点O是位似中心.若OA=2AD,△ABC的周长为4,则△DEF的周长为( )
A.6 B.8 C.9 D.12
选:A.
8.(3分)我国古代数学家赵爽(公元3~4世纪)在其所著的《勾股圆方图注》中记载过一元二次方程(正根)的几何解法.以方程x2+5x﹣14=0即x(x+5)=14为例说明,记载的方法是:构造如图面积是(x+x+5)2的大正方形.同时它又等于四个矩形的面积加上中间小正方形的面积,即4×14+52=81,因此x=2.则在下列四个构图中,能正确说明方程x2﹣3x﹣10=0解法的构图是( )
A. B.
C. D.
选:C.
二、填空题(本大题有5小题,每小题3分,共15分)
9.(3分)已知,则的值为 .
10.(3分)为迎接六一儿童节到来,某商场规定凡是购物满88元以上都可以获得一次转动转盘的机会.如图(a)所示,当转盘停止时,指针指向哪个区域顾客就获得对应的奖品.转动转盘若干次,其中指针落入优胜奖区域的频率如图(b)所示,则转盘中优胜奖区域的圆心角近似为 72 度.
11.(3分)关于x的一元二次方程x2+2x+k=0有两个不相等的实数根,则k的取值范围是 k<1 .
12.(3分)图(a)是燕尾夹,图(b)是燕尾夹简化的示意图,夹臂AC,BD可分别绕点M,N旋转,不考虑夹臂的粗细,且此时夹嘴闭合(即C,D两点重合),AM=BN=20mm,CM=DN=15mm,MN=8mm.如图(c),当夹子完全张开时(即A,B两点重合),夹嘴间的距离CD的长为 14 mm.
13.(3分)如图,在正方形ABCD中,E是CD边上一点且满足∠CBE=30°,将△BCE沿BE折叠得到△BC′E,C′E与对角线BD交于点F,则的值为 .
三、解答题(本大题有7小题,共61分)
14.(6分)解一元二次方程:
(1)x2+2x=0;
(2)x2﹣6x﹣391=0.
【解答】解:(1)x2+2x=0,
x(x+2)=0,
∴x=0或x+2=0,
∴x1=0,x2=﹣2;
(2)x2﹣6x﹣391=0,
x2﹣6x=391,
x2﹣6x+9=391+9,即(x﹣3)2=400,
∴x﹣3=±20,
∴x1=23,x2=﹣17.
15.(7分)化学实验课上,杨老师带来了Mg(镁)、Al(铝)、Zn(锌)、Cu(铜)四种金属材料及其元素卡片(如图,除正面信息不同外,其余均相同),将四张元素卡片背面朝上洗匀,让学生随机抽取一张,然后用抽取到的金属与盐酸反应来制取氢气.(根据金属活动顺序可知:Mg、Al、Zn可以置换出氢气,而Cu不能置换出氢气)
(1)小云随机从中抽取一张卡片,抽到“Al”的概率为 ;
(2)小云随机从中抽取一张卡片,记下金属后,放回洗匀,小南再从中随机抽取一张,请用列表或画树状图的方法求小云和小南抽到的金属均能置换出氢气的概率.
【解答】解:(1)由题意知,共有4种等可能的结果,其中抽到“Al”的结果有1种,
∴小云随机从中抽取一张卡片,抽到“Al”的概率为.
故答案为:.
(2)列表如下:
Mg Al Zn Cu
Mg (Mg,Mg) (Mg,Al) (Mg,Zn) (Mg,Cu)
Al (Al,Mg) (Al,Al) (Al,Zn) (Al,Cu)
Zn (Zn,Mg) (Zn,Al) (Zn,Zn) (Zn,Cu)
Cu (Cu,Mg) (Cu,Al) (Cu,Zn) (Cu,Cu)
共有16种等可能的结果,其中小云和小南抽到的金属均能置换出氢气的结果有:(Mg,Mg),(Mg,Al),(Mg,Zn),(Al,Mg),(Al,Al),(Al,Zn),(Zn,Mg),(Zn,Al),(Zn,Zn),共9种,
∴小云和小南抽到的金属均能置换出氢气的概率为.
16.(8分)如图,在平行四边形ABCD中,∠BDC=90°,E是AD边上一点,延长BE与CD的延长线交于点F,连接AF.
(1)请从下列条件中选择一个能证明四边形ABDF是矩形的条件,并写出证明过程;
①AE=DE;②BF=BC;③AE=BE.
(2)若四边形ABDF是矩形,且AB=3,AD=5,求四边形ABCF的面积.
【解答】解:(1)选①AE=DE.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABE=∠DFE,
在△ABE和△DFE中,
,
∴△ABE≌△DFE(AAS),
∴AB=DF,
∵AB∥DF,AB=DF,
∴四边形ABDF是平行四边形,
∵∠BDC=90°,
∴∠BDF=90°,
∴四边形ABDF是矩形;
(2)解:∵四边形ABDF是矩形,
∴AB=DF,
∵四边形ABDF是平行四边形,
∴AB=CD,
∴AB=DF=CD=3,
∴CF=DF+CD=3+3=6,
在Rt△BDC中,BC=AD=5,CD=3,
∴BD===4,
∵AB∥CF,
∴S=BD(AB+CF)=×4×(3+6)=18,
∴四边形ABCF的面积S等于18.
17.(8分)已知甲商品每件的进价为20元,售价为每件40元.
(1)若商场计划对甲商品降价促销,预备从原来售价的每件40元进行两次调价后将售价降为每件32.4元.若甲商品两次调价的降价率相同,求这个降价率;
(2)经调查,甲商品每降价1元时,每月可多销售10件.已知甲商品在原售价为每件40元时的月销售量为100件.若商场希望甲商品该月的获利为2250元,请问甲商品在原售价的基础上应降价多少元?
【解答】解:(1)设这个降价率为x,
依题意得:40(1﹣x)2=32.4,
解得:x1=0.1=10%,x2=1.9(不符合题意,舍去),
答:这个降价率为10%;
(2)设甲商品在原售价的基础上应降价y元,则每月销售量为(100+10x)件,
依题意得:(40﹣20﹣y)(100+10y)=2250,
整理得:y2﹣10y+25=0,
解得:y1=y2=5,
答:甲商品在原售价的基础上应降价5元.
18.(10分)综合与实践
背景 晚上小明在广场上散步,如图(a)所示,AB,CD是广场上的两根电线杆,小明站在点E处,在两盏路灯B,D的照射下,地面上形成了他的两个影子EH,EG.
素材1 两盏路灯B,D的高均为10m,两盏路灯相距40m,小明的身高EF为1.5m.
素材2 A,C,E,G,H在同一平面内,电线杆和人均垂直于地面.
问题提出 小明在广场中走动时(始终保证影子EG,EH不为0),两个影子端点间的距离GH是否会发生改变?
问题解决
任务1 计算 (1)如图(b),当小明影子EG长为4.5m时,此时小明到电线杆CD的距离EC为多少?
任务2 说理 (2)小明在广场上走动的过程中两个影子端点间的距离GH是否会改变?若GH的长不变,请求出GH的长;若GH的长度发生变化,请说明理由.
任务3 拓展 (3)小明在广场的某个位置向上跳起再落下,在该过程中GH最长达到10m,请直接写出小明从起跳到落下的过程中,头顶距离地面的最大高度.
【解答】解:(1)根据题意,EF∥AB∥CD,AB=CD.
∴=,
∴===.
当EG=4.5m时,CE==25.5m.
故小明到电线杆CD的距离EC为25.5m.
(2)由(1)得==.
又∵∠HEG=∠AEC,
∴△HEG∽△AEC,
∴.
又∵AC=40m,
∴GH=AC =m.
故GH的长度不会改变,GH=m.
(3)由(2)可知.
∴GH==.
当小明跳起时,EF变大,(﹣1)变小,GH变大,当小明跳到最高点时,GH最大长度为10m.
∴10=.
解得EF=2m.
故从起跳到落下的过程中,头顶距离地面的最大高度为2m.
19.(11分)综合与探究
【定义】我们把关于x的一元二次方程ax2+bx+c=0与cx2+bx+a=0(ac≠0,a≠c)称为一对“友好方程”.
【示例】如2x2+7x﹣3=0的“友好方程”是﹣3x2+7x+2=0.
(1)写出一元二次方程12x2﹣7x+1=0的“友好方程”是 x2﹣7x+12=0 .
【探究】
(2)已知一元二次方程12x2﹣7x+1=0的两根为,,请求出它的“友好方程”的两个根.
【猜想】.
(3)当Δ=b2﹣4ac≥0时,方程ax2+bx+c=0的两根x1,x2与其“友好方程”cx2+bx+a=0的两根x3,x4之间存在的一种特殊关系为 互为倒数 .(ac≠0,a≠c)
【证明】
∵方程ax2+bx+c=0的两根为,;
方程cx2+bx+a=0的两根为,① x4= ;
…
(4)请完成上述填空①,并补全证明过程.(备注:证明一组关系即可)
【拓展】
(5)已知关于x的方程2024x2+bx﹣c=0的两根是x1=﹣1,,请利用上述结论,直接写出关于x的方程c(x﹣1)2﹣bx+b=2024的两根.
【解答】解:(1)一元二次方程12x2﹣7x+1=0的“友好方程”为:x2﹣7x+12=0,
故答案为:x2﹣7x+12=0;
(2)x2﹣7x+12=0,
(x﹣3)(x﹣4)=0,
解得x1=3,x2=4;
(3)根据(2)的结论,猜想当Δ=b2﹣4ac≥0时,ax2+bx+c=0的两根x1、x2与其“友好方程”cx2+bx+a=0的两根x3、x4之间存在的一种特殊关系为互为倒数,(ac≠0,a≠c),
故答案为:互为倒数;
(4)证明如下:
∵方程ax2+bx+c=0的两根为,;
“友好方程”cx2+bx+a=0的两根为,x4=,
∴x1 x4= ===1,x2 x3= ===1,
即原方程的两根与“友好方程”的两根互为倒数,
故答案为:x4=;
(5)关于x的方程2024x2+bx﹣c=0的两根是x1=﹣1,,
∴该方程的“友好方程”﹣cx2+bx+2024=0,即cx2﹣bx﹣2024=0的两根为x1=﹣1,x2=2024,
则c(x﹣1)2﹣bx+b=2024,即c(x﹣1)2﹣b(x﹣1)﹣2024=0中x﹣1=﹣1或x﹣1=2024,
∴该方程的解为x1=0,x2=2025.
20.(11分)综合与探究
如图,在平行四边形ABCD中,E,F分别是边BC,CD上的点,AE与BF交于点P.
(1)【特例感知】
如图(a),若四边形ABCD是正方形,当∠APB=∠D时,则线段AE与BF的数量关系是 AE=BF ;
(2)【深入探究】
如图(b),若四边形ABCD是菱形,且∠APB=∠D,则线段AE与BF满足怎样的数量关系?请证明你的猜想;关于此问,数学兴趣小组给出如下两种解决思路.请选择其中一种思路解决问题.
思路一 思路二
如图,在BC边上取一点M使AM=AB,… 如图,在CB的延长线上取一点N使AN=AE,…
(3)【类比迁移】
如图(c),若四边形ABCD是菱形,E为BC的中点,∠APB=∠C=60°,请求出的值;
(4)【联系拓广】
如图(d),在平行四边形ABCD中,AD=3,AB=4,∠C=60°,F是CD边的中点,当点E在直线BC上运动,且直线AE与直线BF所夹的锐角为60°时,请直接写BE的长.
【解答】解:(1)当四边形ABCD是正方形,∠APB=∠D=90°.
∴∠BAP+∠ABP=∠BAP+∠EBP=90°.
∴∠ABP=∠EBP.
又∵AB=BC,∠ABC=∠C.
∴△ABE≌△BCF(ASA).
∴AE=BF.
故答案为:AE=BF.
(2)猜想AE=BF.
证明:
思路一:如图,在BC上取一点M,使AB=AM,则∠ABM=∠AMB.
∵四边形ABCD是菱形.
∴AB∥CD,AB=BC=AM,∠ABM+∠C=180°,∠D=∠ABE.
∵∠AME+∠AMB=180°,∠ABM+∠C=180°,
∴∠AME=∠C.
∵∠APB=∠D=∠ABM=∠AMB=60°,
∴∠FBC=∠APB﹣∠AEM=∠AMB﹣∠AEM=∠EAM.
在△AEM和△BFC中,∠FBC=∠EAM,AM=BC,∠AME=∠C,
∴△AEM≌△BFC(ASA).
∴AE=BF.
思路二:如图,在CB延长线上取点N,使AN=AE,则∠ANB=∠AEB.
根据菱形的性质∠ABC+∠C=180°,
∴∠ABN=∠C.
又∵∠BAN=∠ABC﹣∠ANB,∠APB﹣∠AEB=∠CBF,
∴∠BAN=∠CBF.
在△ABN和△BCF中,∠BAN=∠CBF,AB=BC,∠ABN=∠C,
∴△ABN≌△BCF(AAS).
∴AN=BF,
∴AE=BF.
(3)如图,延长AB,使BG=BE.
∵AB∥CD,
∴∠BGC=∠C=60°,
∴△BGE是等边三角形.
∴∠G=60°,BG=BE=BC=AB.
∵∠BAE+∠BEA=∠BGC,∠PBE+∠BEP=∠APB,∠APB=∠C=60°,
∴∠BAE=∠PBE.
在△EAG和△FBC中,∠GAE=∠CBF,∠G=∠C,
∴△EAG∽△FBC.
∴===.
(4)如图,AE、AE′分别与直线BF相交于G、I,∠AIB=∠AGB=60°.
∴△AGI为等边三角形.
过点F作FJ⊥BC,垂足为J,则JC=FC cosC=,FJ=FC sinC=FC.
又∵FC==2,
∴JC=1,FJ=,BJ=BC﹣JC=2,BF==.
∵AB∥CD,
∴∠ABI=∠BFC,
又∵∠AIB=∠C=60°
∴△ABI∽△BFC.
∴.即,
∴AI=,BI=
∴AG=GI=AI=,GB=GI﹣BI=.
在△BAE和△GAB中,∠BAE=∠GAB,∠AGB=∠ABE=60°,
∴△BAE∽△GAB.
∴=,
∴BE=,AE=.
在△GAB和△AE′E中,∠GAB=60°﹣∠E′AB=∠AE′E,∠E′AE=∠AGB=60°,
∴△GAB∽△AE′E.
∴,则E′E=,
∴BE′=E′E﹣BE=8.
故BE的长度为或8.
同课章节目录
