浙江省杭州市西湖区公益中学2024-2025学年九年级(上)期中数学试卷(含答案)
文档属性
| 名称 | 浙江省杭州市西湖区公益中学2024-2025学年九年级(上)期中数学试卷(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 540.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-18 16:10:10 | ||
图片预览




文档简介
2024-2025学年浙江省杭州市西湖区公益中学九年级(上)期中数学试卷
一.选择题(共10小题,每小题3分,共30分)
1.(3分)下列属于二次函数的是( )
A.y=ax2+bx+c B.y=
C.y=ab D.y=x2
2.(3分)如果a和b都不为零,且3a=4b,那么下列比例中正确的是( )
A. B. C. D.
3.(3分)将抛物线y=﹣5x2+1向左平移1个单位,再向下平移2个单位,所得的抛物线为( )
A.y=﹣5(x﹣1)2﹣1 B.y=﹣5(x﹣1)2﹣2
C.y=﹣5(x+1)2﹣1 D.y=﹣5(x+1)2+3
4.(3分)如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为E.若OD=10,BE=4,则CD的长为( )
A.6 B.16 C.8 D.12
5.(3分)如图,两条直线AC和DF被三条平行线所截,交点分别为A、B、C和D、E、F,若AB:BC=2:3,DE=3,则EF的长为( )
A.4.5 B.5 C.6 D.8
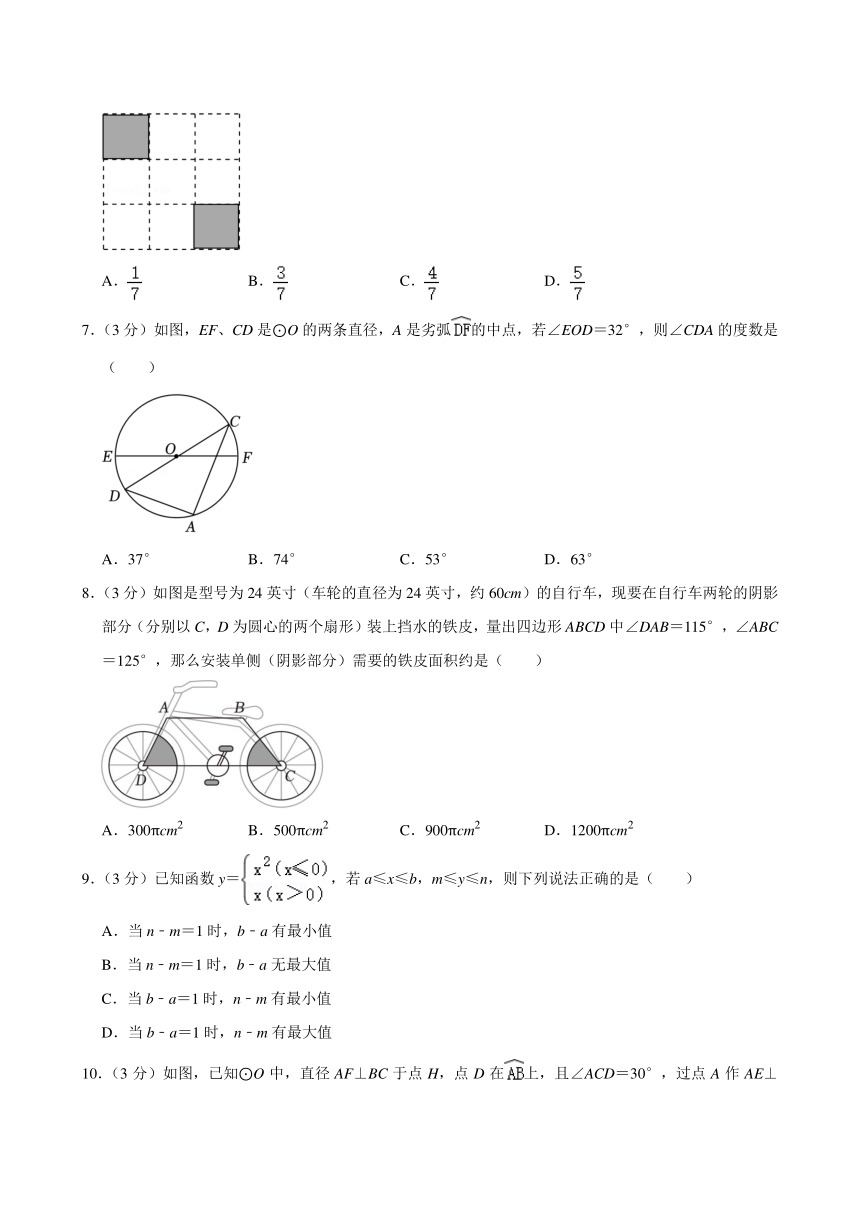
6.(3分)如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中剩余的小正方形中任意一个涂黑,则三个被涂黑的小正方形能构成轴对称图形的概率是( )
A. B. C. D.
7.(3分)如图,EF、CD是⊙O的两条直径,A是劣弧的中点,若∠EOD=32°,则∠CDA的度数是( )
A.37° B.74° C.53° D.63°
8.(3分)如图是型号为24英寸(车轮的直径为24英寸,约60cm)的自行车,现要在自行车两轮的阴影部分(分别以C,D为圆心的两个扇形)装上挡水的铁皮,量出四边形ABCD中∠DAB=115°,∠ABC=125°,那么安装单侧(阴影部分)需要的铁皮面积约是( )
A.300πcm2 B.500πcm2 C.900πcm2 D.1200πcm2
9.(3分)已知函数y=,若a≤x≤b,m≤y≤n,则下列说法正确的是( )
A.当n﹣m=1时,b﹣a有最小值
B.当n﹣m=1时,b﹣a无最大值
C.当b﹣a=1时,n﹣m有最小值
D.当b﹣a=1时,n﹣m有最大值
10.(3分)如图,已知⊙O中,直径AF⊥BC于点H,点D在上,且∠ACD=30°,过点A作AE⊥CD于点E,已知△BCD的周长为,且BH=2,则⊙O的半径长为( )
A. B. C. D.
二.填空题(共6小题,每小题3分,共18分)
11.(3分)已知二次函数y=x2+bx+c(a≠0)的图象经过点A(﹣1,﹣1)、B(5,﹣1),那么该二次函数图象的对称轴为直线 .
12.(3分)AB=10,P是AB的黄金分割点,(BP>AP),BP= .
13.(3分)在一个不透明的袋子中装有6个白球,m个黑球,这些球除颜色外都相同.若从袋子中随机摸出1个球,摸到白球的概率为,则m的值为 .
14.(3分)如图,已知△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕A点逆时针旋转50°得到△AB'C',则∠BB'C′= .
15.(3分)已知⊙O的直径AB=10cm,CD是⊙O的弦,AE⊥CD,垂足为点E,BF⊥CD,垂足为点F,且CD=8cm,则BF﹣AE的长为 cm.
16.(3分)在平面直角坐标系xOy中,A(x1,y1),B(x2,y2),C(x3,y3)是二次函数y=﹣x2+4x﹣1图象上三点.若0<x1<1,x2>4,则y1 y2(填“>”或“<”);若对于m<x1<m+1,m+1<x2<m+2,m+2<x3<m+3,存在y1<y3<y2,则m的取值范围是 .
三.解答题(共8小题,共72分)
17.(9分)如果,且3a﹣2b+c=12,求a﹣b+c的值.
18.(9分)在学习概率的课堂上,老师提出问题:只有一张电影票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小明和小刚都公平的方案.
甲同学的方案:将红桃2、3、4、5四张牌背面向上,小明先抽一张,小刚从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小明看电影,否则小刚看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃2、3、4三张牌,抽取方式及规则不变,乙的方案公平吗?(只回答,不说明理由)
19.(9分)如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.
(1)求此抛物线的解析式;
(2)求△BCD的面积.
20.(9分)如图,已知△ABC,以AB为直径的⊙O分别交AC,BC于点D,E.连接DE,且ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2.求CD的长.
21.(9分)如图,在△ABC中,AB=AC,点D、B、C、E在同一条直线上,且∠D=∠CAE.
(1)求证:△ABD∽△ECA;
(2)若AC=6,CE=4,求BD的长度.
22.(9分)大学毕业生小李自主创业,开了一家小商品超市.已知超市中某商品的进价为每件20元,售价为每件30元,每个月可卖出180件;如果每件商品的售价每上涨1元,则每个月就会少卖出10件,但每件售价必须低于34元,设每件商品的售价上涨x元(x为非负整数),每个月的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)利用函数关系式求出每件商品的售价为多少元时,每个月可获得最大利润?最大利润是多少?
(3)利用函数关系式求出每件商品的售价为多少元时,每个月的利润恰好是1920元?
23.(9分)已知二次函数y=mx2﹣2mx+3,其中m≠0.
(1)若二次函数经过(﹣1,6),求二次函数解析式.
(2)若该抛物线开口向上,当﹣1≤x≤2时,抛物线的最高点为M,最低点为N,点M的纵坐标为6,求点M和点N的坐标.
(3)在二次函数图象上任取两点(x1,y1),(x2,y2),当a≤x1<x2≤a+2时,总有y1>y2,求a的取值范围.
24.(9分)如图,△ABC内接于⊙O,BC是⊙O的直径,E是上一点,弦BE交AC于点F,弦AD⊥BE于点G,连接CD、CG,且∠CBE=∠ACG.
(1)求证:∠CAG=∠ABE;
(2)求证:CG=CD;
(3)若AB=4,BC=2,求GF的长.
2024-2025学年浙江省杭州市西湖区公益中学九年级(上)期中数学试卷
参考答案
一.选择题(共10小题,每小题3分,共30分)
1.(3分)下列属于二次函数的是( )
A.y=ax2+bx+c B.y=
C.y=ab D.y=x2
选:D.
2.(3分)如果a和b都不为零,且3a=4b,那么下列比例中正确的是( )
A. B. C. D.
选:B.
3.(3分)将抛物线y=﹣5x2+1向左平移1个单位,再向下平移2个单位,所得的抛物线为( )
A.y=﹣5(x﹣1)2﹣1 B.y=﹣5(x﹣1)2﹣2
C.y=﹣5(x+1)2﹣1 D.y=﹣5(x+1)2+3
选:C.
4.(3分)如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为E.若OD=10,BE=4,则CD的长为( )
A.6 B.16 C.8 D.12
选:B.
5.(3分)如图,两条直线AC和DF被三条平行线所截,交点分别为A、B、C和D、E、F,若AB:BC=2:3,DE=3,则EF的长为( )
A.4.5 B.5 C.6 D.8
选:A.
6.(3分)如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中剩余的小正方形中任意一个涂黑,则三个被涂黑的小正方形能构成轴对称图形的概率是( )
A. B. C. D.
选:B.
7.(3分)如图,EF、CD是⊙O的两条直径,A是劣弧的中点,若∠EOD=32°,则∠CDA的度数是( )
A.37° B.74° C.53° D.63°
选:C.
8.(3分)如图是型号为24英寸(车轮的直径为24英寸,约60cm)的自行车,现要在自行车两轮的阴影部分(分别以C,D为圆心的两个扇形)装上挡水的铁皮,量出四边形ABCD中∠DAB=115°,∠ABC=125°,那么安装单侧(阴影部分)需要的铁皮面积约是( )
A.300πcm2 B.500πcm2 C.900πcm2 D.1200πcm2
选:A.
9.(3分)已知函数y=,若a≤x≤b,m≤y≤n,则下列说法正确的是( )
A.当n﹣m=1时,b﹣a有最小值
B.当n﹣m=1时,b﹣a无最大值
C.当b﹣a=1时,n﹣m有最小值
D.当b﹣a=1时,n﹣m有最大值
选:C.
10.(3分)如图,已知⊙O中,直径AF⊥BC于点H,点D在上,且∠ACD=30°,过点A作AE⊥CD于点E,已知△BCD的周长为,且BH=2,则⊙O的半径长为( )
A. B. C. D.
选:D.
二.填空题(共6小题,每小题3分,共18分)
11.(3分)已知二次函数y=x2+bx+c(a≠0)的图象经过点A(﹣1,﹣1)、B(5,﹣1),那么该二次函数图象的对称轴为直线 x=2 .
12.(3分)AB=10,P是AB的黄金分割点,(BP>AP),BP= .
13.(3分)在一个不透明的袋子中装有6个白球,m个黑球,这些球除颜色外都相同.若从袋子中随机摸出1个球,摸到白球的概率为,则m的值为 12 .
14.(3分)如图,已知△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕A点逆时针旋转50°得到△AB'C',则∠BB'C′= 95° .
15.(3分)已知⊙O的直径AB=10cm,CD是⊙O的弦,AE⊥CD,垂足为点E,BF⊥CD,垂足为点F,且CD=8cm,则BF﹣AE的长为 6 cm.
16.(3分)在平面直角坐标系xOy中,A(x1,y1),B(x2,y2),C(x3,y3)是二次函数y=﹣x2+4x﹣1图象上三点.若0<x1<1,x2>4,则y1 > y2(填“>”或“<”);若对于m<x1<m+1,m+1<x2<m+2,m+2<x3<m+3,存在y1<y3<y2,则m的取值范围是 ﹣<m<1 .
三.解答题(共8小题,共72分)
17.(9分)如果,且3a﹣2b+c=12,求a﹣b+c的值.
【解答】解:令===k,
∴a=3k,b=4k,c=5k,
∵3a﹣2b+c=12,
∴9k﹣8k+5k=12,
∴k=2,
∴a=3k=6,b=4k=8,c=5k=10,
∴a﹣b+c=6﹣8+10=8.
18.(9分)在学习概率的课堂上,老师提出问题:只有一张电影票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小明和小刚都公平的方案.
甲同学的方案:将红桃2、3、4、5四张牌背面向上,小明先抽一张,小刚从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小明看电影,否则小刚看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃2、3、4三张牌,抽取方式及规则不变,乙的方案公平吗?(只回答,不说明理由)
【解答】解:(1)甲同学的方案不公平.理由如下:
列表法,
小明小刚 2 3 4 5
2 (2,3) (2,4) (2,5)
3 (3,2) (3,4) (3,5)
4 (4,2) (4,3) (4,5)
5 (5,2) (5,3) (5,4)
所有可能出现的结果共有12种,其中抽出的牌面上的数字之和为奇数的有:8种,故小明获胜的概率为:=,则小刚获胜的概率为:,
故此游戏两人获胜的概率不相同,即他们的游戏规则不公平;
(2)不公平.理由如下:
小明小刚 2 3 4
2 (2,3) (2,4)
3 (3,2) (3,4)
4 (4,2) (4,3)
所有可能出现的结果共有6种,其中抽出的牌面上的数字之和为奇数的有:4种,故小明获胜的概率为:=,则小刚获胜的概率为:,
故此游戏两人获胜的概率不相同,即他们的游戏规则不公平.
19.(9分)如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.
(1)求此抛物线的解析式;
(2)求△BCD的面积.
【解答】解:(1)∵抛物线的顶点为A(1,4),
∴设抛物线的解析式y=a(x﹣1)2+4,
把点B(0,3)代入得:a+4=3,
解得:a=﹣1,
∴抛物线的解析式为y=﹣(x﹣1)2+4;
(2)由(1)知,抛物线的解析式为y=﹣(x﹣1)2+4;
令y=0,则0=﹣(x﹣1)2+4,
∴x=﹣1或x=3,
∴C(﹣1,0),D(3,0);
∴CD=4,
∴S△BCD=CD×|yB|=×4×3=6.
20.(9分)如图,已知△ABC,以AB为直径的⊙O分别交AC,BC于点D,E.连接DE,且ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2.求CD的长.
【解答】(1)证明:∵ED=EC,
∴∠EDC=∠C,
∵∠EDC=∠B,(∵∠EDC+∠ADE=180°,∠B+∠ADE=180°,∴∠EDC=∠B)
∴∠B=∠C,
∴AB=AC;
(2)方法一:
解:连接AE,
∵AB为直径,
∴AE⊥BC,
由(1)知AB=AC,
∴BE=CE=BC=,
∵△CDE∽△CBA,
∴,
∴CE CB=CD CA,AC=AB=4,
∴ 2=4CD,
∴CD=.
方法二:
解:连接BD,
∵AB为直径,
∴BD⊥AC,
设CD=a,
由(1)知AC=AB=4,
则AD=4﹣a,
在Rt△ABD中,由勾股定理可得:
BD2=AB2﹣AD2=42﹣(4﹣a)2
在Rt△CBD中,由勾股定理可得:
BD2=BC2﹣CD2=(2)2﹣a2
∴42﹣(4﹣a)2=(2)2﹣a2
整理得:a=,
即:CD=.
21.(9分)如图,在△ABC中,AB=AC,点D、B、C、E在同一条直线上,且∠D=∠CAE.
(1)求证:△ABD∽△ECA;
(2)若AC=6,CE=4,求BD的长度.
【解答】(1)证明:∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABD=∠ACE,
∵∠D=∠CAE.
∴△ABD∽△ECA;
(2)解:∵AB=AC,AC=6,
∴AB=AC=6,
∵△ABD∽△ECA,
∴,
∴,
∴BD=9.
22.(9分)大学毕业生小李自主创业,开了一家小商品超市.已知超市中某商品的进价为每件20元,售价为每件30元,每个月可卖出180件;如果每件商品的售价每上涨1元,则每个月就会少卖出10件,但每件售价必须低于34元,设每件商品的售价上涨x元(x为非负整数),每个月的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)利用函数关系式求出每件商品的售价为多少元时,每个月可获得最大利润?最大利润是多少?
(3)利用函数关系式求出每件商品的售价为多少元时,每个月的利润恰好是1920元?
【解答】解:(1)由题意得:y=(30﹣20﹣x)(180﹣10x),
整理得:y=﹣10x2+80x+1800,
答:y=﹣10x2+80x+1800,自变量x的取值范围为0≤x<4,且x为整数;
(2)y=﹣10x2+80x+1800=﹣10(x﹣4)2+1960,
∵﹣10<0,
∴当x<4时,y随x的增大而增大,
∵当0≤x<4,且x为整数时,
∴当x=3时,最大值y=﹣10(3﹣4)2+1960=1950(元),
此时售价为30+3=33(元);
答:每件商品售价为33元时,每个月可获得最大利润,最大利润为1950元;
(3)由题意得:﹣10x2+80x+1800=1920,
解得:x1=2,x2=6;
∵0≤x<4,且x为整数,
∴x=2,
此时售价为30+2=32(元);
答:每件商品售价为32元时,每个月可获得的利润恰好为1920元.
23.(9分)已知二次函数y=mx2﹣2mx+3,其中m≠0.
(1)若二次函数经过(﹣1,6),求二次函数解析式.
(2)若该抛物线开口向上,当﹣1≤x≤2时,抛物线的最高点为M,最低点为N,点M的纵坐标为6,求点M和点N的坐标.
(3)在二次函数图象上任取两点(x1,y1),(x2,y2),当a≤x1<x2≤a+2时,总有y1>y2,求a的取值范围.
【解答】解:(1)把(﹣1,6)代入函数解析式得,
m+2m+3=6,
∴m=1,
∴函数解析式为:y=x2﹣2x+3;
(2)∵抛物线开口方向向上,
∴m>0,
∵y=mx2﹣2mx+3=m(x﹣1)2+3﹣m,
∴抛物线的顶点为(1,3﹣m),
∴当x<1时y随x增大而减小,
当x≥1时,y随x增大而增大,
∴最低点N(1,3﹣m),
∵当x=﹣1时,y=3m+3,
当x=2时,y=3,
且m>0,
∴3m+3>3,
∴最高点M(﹣1,3m+3),
∴3m+3=6,
∴m=1,
代入M点和N点坐标得:M(﹣1,6),N(1,2);
(3)①当m>0时,
则有当x≤1时y随x增大而减小,
当x≥1时,y随x增大而增大,
又∵当a≤x1<x2≤a+2时,总有y1>y2,
此时a+2≤1,
∴a≤﹣1,
②当m<0时,
则有当x≤1时y随x增大而增大,
当x≥1时,y随x增大而减小,
又∵当a≤x1<x2≤a+2时,总有y1>y2,
此时a≥1,
综上,当m>0时a≤﹣1;当m<0时,a≥1.
24.(9分)如图,△ABC内接于⊙O,BC是⊙O的直径,E是上一点,弦BE交AC于点F,弦AD⊥BE于点G,连接CD、CG,且∠CBE=∠ACG.
(1)求证:∠CAG=∠ABE;
(2)求证:CG=CD;
(3)若AB=4,BC=2,求GF的长.
【解答】(1)证明:∵BC是⊙O的直径,
∴∠CAB=90°,
∴∠CAG+∠BAG=90°,
∵AD⊥BE,
∴∠AGB=90°,
∴∠BAG+∠ABE=90°,
∴∠CAG=∠ABE;
(2)证明:∵∠CGD=∠CAG+∠ACG,∠ABC=∠ABE+∠CBE,
由(1)知,∠CAG=∠ABE,
∵∠CBE=∠ACG,
∴∠CGD=∠ABC,
∵∠ABC=∠D,
∴∠DGC=∠D,
∴CG=CD;
(3)解:连接AE、CE,
∵BC是直径,
∴∠BEC=90°,
∴∠AGE=∠BEC,
∴AD∥CE,
∵∠CAE=∠EBC,
∠ACG=∠EBC,
∴∠CAE=∠ACG,
∴AE∥CG,
∴四边形AGCE是平行四边形,
∴AF=AC,
∵AC2=BC2﹣AB2,
∴AC2=﹣42,
∴AC=6,
∴AF=×6=3,
∵BF2=AF2+AB2,
∴BF2=32+42,
∴BF=5,
∵∠ABG=∠ABF,∠AGB=∠BAF,
∴△BAG∽△BFA,
∴BA:BF=BG:BA,
∴4:5=BG:4,
∴BG=,
∵FG=BF﹣BG,
∴FG=5﹣=.
一.选择题(共10小题,每小题3分,共30分)
1.(3分)下列属于二次函数的是( )
A.y=ax2+bx+c B.y=
C.y=ab D.y=x2
2.(3分)如果a和b都不为零,且3a=4b,那么下列比例中正确的是( )
A. B. C. D.
3.(3分)将抛物线y=﹣5x2+1向左平移1个单位,再向下平移2个单位,所得的抛物线为( )
A.y=﹣5(x﹣1)2﹣1 B.y=﹣5(x﹣1)2﹣2
C.y=﹣5(x+1)2﹣1 D.y=﹣5(x+1)2+3
4.(3分)如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为E.若OD=10,BE=4,则CD的长为( )
A.6 B.16 C.8 D.12
5.(3分)如图,两条直线AC和DF被三条平行线所截,交点分别为A、B、C和D、E、F,若AB:BC=2:3,DE=3,则EF的长为( )
A.4.5 B.5 C.6 D.8
6.(3分)如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中剩余的小正方形中任意一个涂黑,则三个被涂黑的小正方形能构成轴对称图形的概率是( )
A. B. C. D.
7.(3分)如图,EF、CD是⊙O的两条直径,A是劣弧的中点,若∠EOD=32°,则∠CDA的度数是( )
A.37° B.74° C.53° D.63°
8.(3分)如图是型号为24英寸(车轮的直径为24英寸,约60cm)的自行车,现要在自行车两轮的阴影部分(分别以C,D为圆心的两个扇形)装上挡水的铁皮,量出四边形ABCD中∠DAB=115°,∠ABC=125°,那么安装单侧(阴影部分)需要的铁皮面积约是( )
A.300πcm2 B.500πcm2 C.900πcm2 D.1200πcm2
9.(3分)已知函数y=,若a≤x≤b,m≤y≤n,则下列说法正确的是( )
A.当n﹣m=1时,b﹣a有最小值
B.当n﹣m=1时,b﹣a无最大值
C.当b﹣a=1时,n﹣m有最小值
D.当b﹣a=1时,n﹣m有最大值
10.(3分)如图,已知⊙O中,直径AF⊥BC于点H,点D在上,且∠ACD=30°,过点A作AE⊥CD于点E,已知△BCD的周长为,且BH=2,则⊙O的半径长为( )
A. B. C. D.
二.填空题(共6小题,每小题3分,共18分)
11.(3分)已知二次函数y=x2+bx+c(a≠0)的图象经过点A(﹣1,﹣1)、B(5,﹣1),那么该二次函数图象的对称轴为直线 .
12.(3分)AB=10,P是AB的黄金分割点,(BP>AP),BP= .
13.(3分)在一个不透明的袋子中装有6个白球,m个黑球,这些球除颜色外都相同.若从袋子中随机摸出1个球,摸到白球的概率为,则m的值为 .
14.(3分)如图,已知△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕A点逆时针旋转50°得到△AB'C',则∠BB'C′= .
15.(3分)已知⊙O的直径AB=10cm,CD是⊙O的弦,AE⊥CD,垂足为点E,BF⊥CD,垂足为点F,且CD=8cm,则BF﹣AE的长为 cm.
16.(3分)在平面直角坐标系xOy中,A(x1,y1),B(x2,y2),C(x3,y3)是二次函数y=﹣x2+4x﹣1图象上三点.若0<x1<1,x2>4,则y1 y2(填“>”或“<”);若对于m<x1<m+1,m+1<x2<m+2,m+2<x3<m+3,存在y1<y3<y2,则m的取值范围是 .
三.解答题(共8小题,共72分)
17.(9分)如果,且3a﹣2b+c=12,求a﹣b+c的值.
18.(9分)在学习概率的课堂上,老师提出问题:只有一张电影票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小明和小刚都公平的方案.
甲同学的方案:将红桃2、3、4、5四张牌背面向上,小明先抽一张,小刚从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小明看电影,否则小刚看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃2、3、4三张牌,抽取方式及规则不变,乙的方案公平吗?(只回答,不说明理由)
19.(9分)如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.
(1)求此抛物线的解析式;
(2)求△BCD的面积.
20.(9分)如图,已知△ABC,以AB为直径的⊙O分别交AC,BC于点D,E.连接DE,且ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2.求CD的长.
21.(9分)如图,在△ABC中,AB=AC,点D、B、C、E在同一条直线上,且∠D=∠CAE.
(1)求证:△ABD∽△ECA;
(2)若AC=6,CE=4,求BD的长度.
22.(9分)大学毕业生小李自主创业,开了一家小商品超市.已知超市中某商品的进价为每件20元,售价为每件30元,每个月可卖出180件;如果每件商品的售价每上涨1元,则每个月就会少卖出10件,但每件售价必须低于34元,设每件商品的售价上涨x元(x为非负整数),每个月的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)利用函数关系式求出每件商品的售价为多少元时,每个月可获得最大利润?最大利润是多少?
(3)利用函数关系式求出每件商品的售价为多少元时,每个月的利润恰好是1920元?
23.(9分)已知二次函数y=mx2﹣2mx+3,其中m≠0.
(1)若二次函数经过(﹣1,6),求二次函数解析式.
(2)若该抛物线开口向上,当﹣1≤x≤2时,抛物线的最高点为M,最低点为N,点M的纵坐标为6,求点M和点N的坐标.
(3)在二次函数图象上任取两点(x1,y1),(x2,y2),当a≤x1<x2≤a+2时,总有y1>y2,求a的取值范围.
24.(9分)如图,△ABC内接于⊙O,BC是⊙O的直径,E是上一点,弦BE交AC于点F,弦AD⊥BE于点G,连接CD、CG,且∠CBE=∠ACG.
(1)求证:∠CAG=∠ABE;
(2)求证:CG=CD;
(3)若AB=4,BC=2,求GF的长.
2024-2025学年浙江省杭州市西湖区公益中学九年级(上)期中数学试卷
参考答案
一.选择题(共10小题,每小题3分,共30分)
1.(3分)下列属于二次函数的是( )
A.y=ax2+bx+c B.y=
C.y=ab D.y=x2
选:D.
2.(3分)如果a和b都不为零,且3a=4b,那么下列比例中正确的是( )
A. B. C. D.
选:B.
3.(3分)将抛物线y=﹣5x2+1向左平移1个单位,再向下平移2个单位,所得的抛物线为( )
A.y=﹣5(x﹣1)2﹣1 B.y=﹣5(x﹣1)2﹣2
C.y=﹣5(x+1)2﹣1 D.y=﹣5(x+1)2+3
选:C.
4.(3分)如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为E.若OD=10,BE=4,则CD的长为( )
A.6 B.16 C.8 D.12
选:B.
5.(3分)如图,两条直线AC和DF被三条平行线所截,交点分别为A、B、C和D、E、F,若AB:BC=2:3,DE=3,则EF的长为( )
A.4.5 B.5 C.6 D.8
选:A.
6.(3分)如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中剩余的小正方形中任意一个涂黑,则三个被涂黑的小正方形能构成轴对称图形的概率是( )
A. B. C. D.
选:B.
7.(3分)如图,EF、CD是⊙O的两条直径,A是劣弧的中点,若∠EOD=32°,则∠CDA的度数是( )
A.37° B.74° C.53° D.63°
选:C.
8.(3分)如图是型号为24英寸(车轮的直径为24英寸,约60cm)的自行车,现要在自行车两轮的阴影部分(分别以C,D为圆心的两个扇形)装上挡水的铁皮,量出四边形ABCD中∠DAB=115°,∠ABC=125°,那么安装单侧(阴影部分)需要的铁皮面积约是( )
A.300πcm2 B.500πcm2 C.900πcm2 D.1200πcm2
选:A.
9.(3分)已知函数y=,若a≤x≤b,m≤y≤n,则下列说法正确的是( )
A.当n﹣m=1时,b﹣a有最小值
B.当n﹣m=1时,b﹣a无最大值
C.当b﹣a=1时,n﹣m有最小值
D.当b﹣a=1时,n﹣m有最大值
选:C.
10.(3分)如图,已知⊙O中,直径AF⊥BC于点H,点D在上,且∠ACD=30°,过点A作AE⊥CD于点E,已知△BCD的周长为,且BH=2,则⊙O的半径长为( )
A. B. C. D.
选:D.
二.填空题(共6小题,每小题3分,共18分)
11.(3分)已知二次函数y=x2+bx+c(a≠0)的图象经过点A(﹣1,﹣1)、B(5,﹣1),那么该二次函数图象的对称轴为直线 x=2 .
12.(3分)AB=10,P是AB的黄金分割点,(BP>AP),BP= .
13.(3分)在一个不透明的袋子中装有6个白球,m个黑球,这些球除颜色外都相同.若从袋子中随机摸出1个球,摸到白球的概率为,则m的值为 12 .
14.(3分)如图,已知△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕A点逆时针旋转50°得到△AB'C',则∠BB'C′= 95° .
15.(3分)已知⊙O的直径AB=10cm,CD是⊙O的弦,AE⊥CD,垂足为点E,BF⊥CD,垂足为点F,且CD=8cm,则BF﹣AE的长为 6 cm.
16.(3分)在平面直角坐标系xOy中,A(x1,y1),B(x2,y2),C(x3,y3)是二次函数y=﹣x2+4x﹣1图象上三点.若0<x1<1,x2>4,则y1 > y2(填“>”或“<”);若对于m<x1<m+1,m+1<x2<m+2,m+2<x3<m+3,存在y1<y3<y2,则m的取值范围是 ﹣<m<1 .
三.解答题(共8小题,共72分)
17.(9分)如果,且3a﹣2b+c=12,求a﹣b+c的值.
【解答】解:令===k,
∴a=3k,b=4k,c=5k,
∵3a﹣2b+c=12,
∴9k﹣8k+5k=12,
∴k=2,
∴a=3k=6,b=4k=8,c=5k=10,
∴a﹣b+c=6﹣8+10=8.
18.(9分)在学习概率的课堂上,老师提出问题:只有一张电影票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小明和小刚都公平的方案.
甲同学的方案:将红桃2、3、4、5四张牌背面向上,小明先抽一张,小刚从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小明看电影,否则小刚看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃2、3、4三张牌,抽取方式及规则不变,乙的方案公平吗?(只回答,不说明理由)
【解答】解:(1)甲同学的方案不公平.理由如下:
列表法,
小明小刚 2 3 4 5
2 (2,3) (2,4) (2,5)
3 (3,2) (3,4) (3,5)
4 (4,2) (4,3) (4,5)
5 (5,2) (5,3) (5,4)
所有可能出现的结果共有12种,其中抽出的牌面上的数字之和为奇数的有:8种,故小明获胜的概率为:=,则小刚获胜的概率为:,
故此游戏两人获胜的概率不相同,即他们的游戏规则不公平;
(2)不公平.理由如下:
小明小刚 2 3 4
2 (2,3) (2,4)
3 (3,2) (3,4)
4 (4,2) (4,3)
所有可能出现的结果共有6种,其中抽出的牌面上的数字之和为奇数的有:4种,故小明获胜的概率为:=,则小刚获胜的概率为:,
故此游戏两人获胜的概率不相同,即他们的游戏规则不公平.
19.(9分)如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.
(1)求此抛物线的解析式;
(2)求△BCD的面积.
【解答】解:(1)∵抛物线的顶点为A(1,4),
∴设抛物线的解析式y=a(x﹣1)2+4,
把点B(0,3)代入得:a+4=3,
解得:a=﹣1,
∴抛物线的解析式为y=﹣(x﹣1)2+4;
(2)由(1)知,抛物线的解析式为y=﹣(x﹣1)2+4;
令y=0,则0=﹣(x﹣1)2+4,
∴x=﹣1或x=3,
∴C(﹣1,0),D(3,0);
∴CD=4,
∴S△BCD=CD×|yB|=×4×3=6.
20.(9分)如图,已知△ABC,以AB为直径的⊙O分别交AC,BC于点D,E.连接DE,且ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2.求CD的长.
【解答】(1)证明:∵ED=EC,
∴∠EDC=∠C,
∵∠EDC=∠B,(∵∠EDC+∠ADE=180°,∠B+∠ADE=180°,∴∠EDC=∠B)
∴∠B=∠C,
∴AB=AC;
(2)方法一:
解:连接AE,
∵AB为直径,
∴AE⊥BC,
由(1)知AB=AC,
∴BE=CE=BC=,
∵△CDE∽△CBA,
∴,
∴CE CB=CD CA,AC=AB=4,
∴ 2=4CD,
∴CD=.
方法二:
解:连接BD,
∵AB为直径,
∴BD⊥AC,
设CD=a,
由(1)知AC=AB=4,
则AD=4﹣a,
在Rt△ABD中,由勾股定理可得:
BD2=AB2﹣AD2=42﹣(4﹣a)2
在Rt△CBD中,由勾股定理可得:
BD2=BC2﹣CD2=(2)2﹣a2
∴42﹣(4﹣a)2=(2)2﹣a2
整理得:a=,
即:CD=.
21.(9分)如图,在△ABC中,AB=AC,点D、B、C、E在同一条直线上,且∠D=∠CAE.
(1)求证:△ABD∽△ECA;
(2)若AC=6,CE=4,求BD的长度.
【解答】(1)证明:∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABD=∠ACE,
∵∠D=∠CAE.
∴△ABD∽△ECA;
(2)解:∵AB=AC,AC=6,
∴AB=AC=6,
∵△ABD∽△ECA,
∴,
∴,
∴BD=9.
22.(9分)大学毕业生小李自主创业,开了一家小商品超市.已知超市中某商品的进价为每件20元,售价为每件30元,每个月可卖出180件;如果每件商品的售价每上涨1元,则每个月就会少卖出10件,但每件售价必须低于34元,设每件商品的售价上涨x元(x为非负整数),每个月的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)利用函数关系式求出每件商品的售价为多少元时,每个月可获得最大利润?最大利润是多少?
(3)利用函数关系式求出每件商品的售价为多少元时,每个月的利润恰好是1920元?
【解答】解:(1)由题意得:y=(30﹣20﹣x)(180﹣10x),
整理得:y=﹣10x2+80x+1800,
答:y=﹣10x2+80x+1800,自变量x的取值范围为0≤x<4,且x为整数;
(2)y=﹣10x2+80x+1800=﹣10(x﹣4)2+1960,
∵﹣10<0,
∴当x<4时,y随x的增大而增大,
∵当0≤x<4,且x为整数时,
∴当x=3时,最大值y=﹣10(3﹣4)2+1960=1950(元),
此时售价为30+3=33(元);
答:每件商品售价为33元时,每个月可获得最大利润,最大利润为1950元;
(3)由题意得:﹣10x2+80x+1800=1920,
解得:x1=2,x2=6;
∵0≤x<4,且x为整数,
∴x=2,
此时售价为30+2=32(元);
答:每件商品售价为32元时,每个月可获得的利润恰好为1920元.
23.(9分)已知二次函数y=mx2﹣2mx+3,其中m≠0.
(1)若二次函数经过(﹣1,6),求二次函数解析式.
(2)若该抛物线开口向上,当﹣1≤x≤2时,抛物线的最高点为M,最低点为N,点M的纵坐标为6,求点M和点N的坐标.
(3)在二次函数图象上任取两点(x1,y1),(x2,y2),当a≤x1<x2≤a+2时,总有y1>y2,求a的取值范围.
【解答】解:(1)把(﹣1,6)代入函数解析式得,
m+2m+3=6,
∴m=1,
∴函数解析式为:y=x2﹣2x+3;
(2)∵抛物线开口方向向上,
∴m>0,
∵y=mx2﹣2mx+3=m(x﹣1)2+3﹣m,
∴抛物线的顶点为(1,3﹣m),
∴当x<1时y随x增大而减小,
当x≥1时,y随x增大而增大,
∴最低点N(1,3﹣m),
∵当x=﹣1时,y=3m+3,
当x=2时,y=3,
且m>0,
∴3m+3>3,
∴最高点M(﹣1,3m+3),
∴3m+3=6,
∴m=1,
代入M点和N点坐标得:M(﹣1,6),N(1,2);
(3)①当m>0时,
则有当x≤1时y随x增大而减小,
当x≥1时,y随x增大而增大,
又∵当a≤x1<x2≤a+2时,总有y1>y2,
此时a+2≤1,
∴a≤﹣1,
②当m<0时,
则有当x≤1时y随x增大而增大,
当x≥1时,y随x增大而减小,
又∵当a≤x1<x2≤a+2时,总有y1>y2,
此时a≥1,
综上,当m>0时a≤﹣1;当m<0时,a≥1.
24.(9分)如图,△ABC内接于⊙O,BC是⊙O的直径,E是上一点,弦BE交AC于点F,弦AD⊥BE于点G,连接CD、CG,且∠CBE=∠ACG.
(1)求证:∠CAG=∠ABE;
(2)求证:CG=CD;
(3)若AB=4,BC=2,求GF的长.
【解答】(1)证明:∵BC是⊙O的直径,
∴∠CAB=90°,
∴∠CAG+∠BAG=90°,
∵AD⊥BE,
∴∠AGB=90°,
∴∠BAG+∠ABE=90°,
∴∠CAG=∠ABE;
(2)证明:∵∠CGD=∠CAG+∠ACG,∠ABC=∠ABE+∠CBE,
由(1)知,∠CAG=∠ABE,
∵∠CBE=∠ACG,
∴∠CGD=∠ABC,
∵∠ABC=∠D,
∴∠DGC=∠D,
∴CG=CD;
(3)解:连接AE、CE,
∵BC是直径,
∴∠BEC=90°,
∴∠AGE=∠BEC,
∴AD∥CE,
∵∠CAE=∠EBC,
∠ACG=∠EBC,
∴∠CAE=∠ACG,
∴AE∥CG,
∴四边形AGCE是平行四边形,
∴AF=AC,
∵AC2=BC2﹣AB2,
∴AC2=﹣42,
∴AC=6,
∴AF=×6=3,
∵BF2=AF2+AB2,
∴BF2=32+42,
∴BF=5,
∵∠ABG=∠ABF,∠AGB=∠BAF,
∴△BAG∽△BFA,
∴BA:BF=BG:BA,
∴4:5=BG:4,
∴BG=,
∵FG=BF﹣BG,
∴FG=5﹣=.
同课章节目录
