北师大八年级数学(上)第一章 勾股定理 单元检测卷(含答案)
文档属性
| 名称 | 北师大八年级数学(上)第一章 勾股定理 单元检测卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 999.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-18 18:11:30 | ||
图片预览


文档简介
八年级数学(上)第一章勾股定理单元检测卷
(时间:120分钟 满分:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列四组数,是勾股数的是 ( )
A.0.3,0.4,0.5 B.3,4,5 C.6,7,8 D.32,42,52
2.在 Rt△ABC中,∠C=90°,已知a:b=3:4,c=100,其中a,b,c分别为∠A,∠B,∠C的对边,则b的长为 ( )
A.30 B.60 C.80 D.120
3.下列说法中,正确的是 ( )
A.若(c+a)(c-a)=b2,则△ABC是直角三角形
B.若三角形是直角三角形,三角形的三边为a,b,c,则有
C.以三个连续自然数为三边长一定能构成直角三角形
D.在△ABC中,若∠A:∠B:∠C=3:4:5,则△ABC是直角三角形
4.如图,在△ABC中,AB=AC,AB=5,BC=8,AD 是∠BAC的平分线,则AD的长为 ( )
A.6 B.5 C.4 D.3
5.如图,一块边长24米的正方形绿地四周被小路环绕,点B在正方形的边上,BC=7米,则居民从A→C→B 比从A沿直线AB直接到B处要多走 ( )
A.5米 B.25 米 C.12米 D.6米
6.在单位长度为1的正方形网格中,下面的三角形是直角三角形的是 ( )
7.如图,在中,AD平分交BC于点D, ,则点D到AB的距离是 ( )
A.3 B.4 C.5 D.6
8.某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动.如图,当张角为∠BAF时,顶部边缘B 处离桌面的高度BC为7cm,此时底部边缘A处与C处间的距离AC为24 cm,小组成员调整张角的大小继续探究,最后发现当张角为∠DAF时(点D是点B的对应点),顶部边缘D处到桌面的距离 DE 为20cm,则底部边缘A处与 E之间的距离AE为( )
A.15 cm B.18 cm C.21 cm D.24 cm
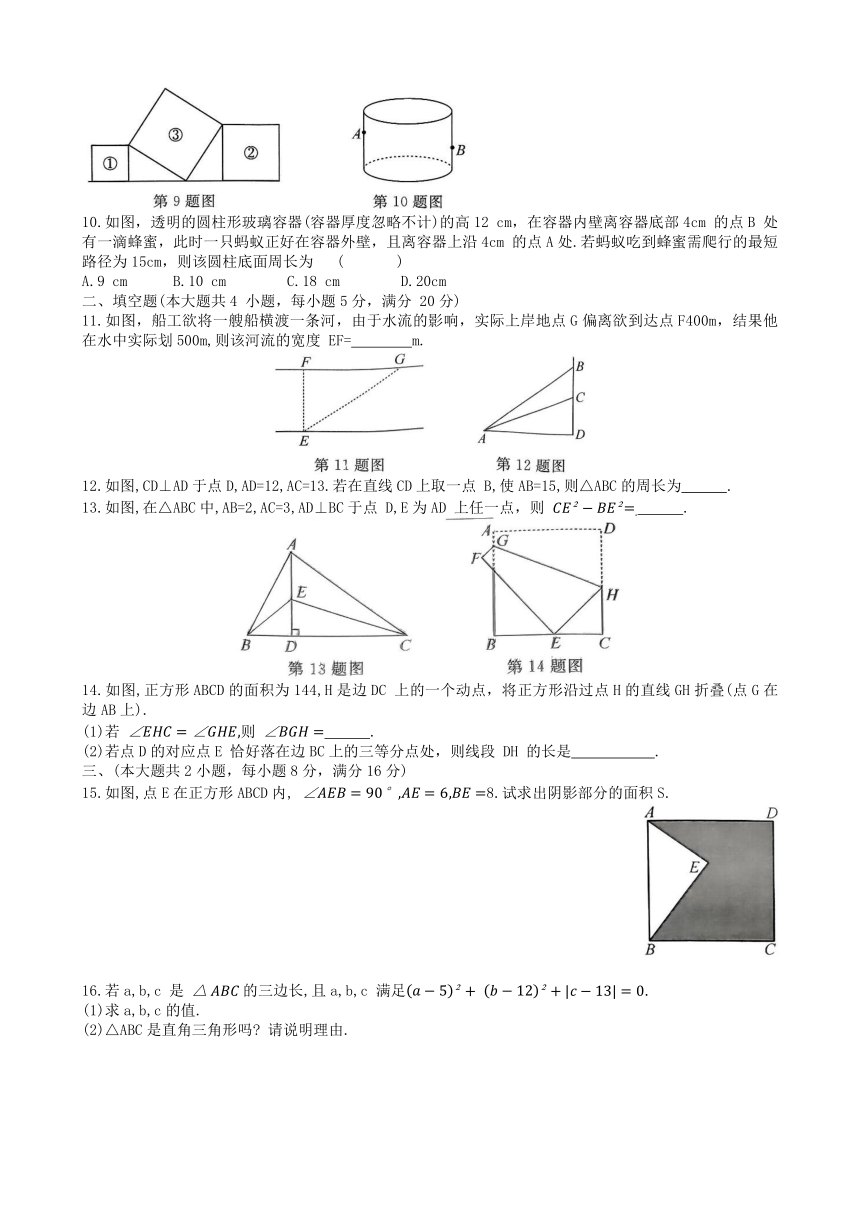
9.将正方形①②③按如图所示的方式放置,若正方形①②的面积分别是81和144,则正方形③的边长为 ( )
A.225 B.63 C.50 D.15
10.如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高12 cm,在容器内壁离容器底部4cm 的点B 处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,且离容器上沿4cm 的点A处.若蚂蚁吃到蜂蜜需爬行的最短路径为15cm,则该圆柱底面周长为 ( )
A.9 cm B.10 cm C.18 cm D.20cm
二、填空题(本大题共4 小题,每小题5分,满分 20分)
11.如图,船工欲将一艘船横渡一条河,由于水流的影响,实际上岸地点G偏离欲到达点F400m,结果他在水中实际划500m,则该河流的宽度 EF= m.
12.如图,CD⊥AD于点D,AD=12,AC=13.若在直线CD上取一点 B,使AB=15,则△ABC的周长为 .
13.如图,在△ABC中,AB=2,AC=3,AD⊥BC于点 D,E为AD 上任一点,则 .
14.如图,正方形ABCD的面积为144,H是边DC 上的一个动点,将正方形沿过点H的直线GH折叠(点G在边AB上).
(1)若 则 .
(2)若点D的对应点E 恰好落在边BC上的三等分点处,则线段 DH 的长是 .
三、(本大题共2小题,每小题8分,满分16分)
15.如图,点E在正方形ABCD内, 8.试求出阴影部分的面积S.
16.若a,b,c 是 的三边长,且a,b,c 满足
(1)求a,b,c的值.
(2)△ABC是直角三角形吗 请说明理由.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,四边形ABCD的周长为42, 是等边三角形, ,求 BC的长.
18.如图,在边长为1的小正方形组成的网格中,点A,B,C都在格点上,请按要求完成下列各题.
.
(2)若△ABC是直角三角形,且边BC的长为5,请在图中确定点C的位置,并补全△ABC.
五、(本大题共2小题,每小题 10分,满分20分)
19.如图,将任意的 Rt△BAC 绕其锐角顶点 A 逆时针旋转90°得到△EAD,则∠BAE=90°,连接BE,延长 BC,DE交于点 F,则四边形ACFD是一个正方形,且它的面积与四边形ABFE的面积相等.四边形 ABFE的面积等于Rt△BAE与Rt△BFE的面积之和.根据图形写出一种验证勾股定理的方法.
20.在一次“探究性学习”课中,老师设计如下数表:
n 2 3 4 5 6
a 22—1 32—1 42—1 52—1
b 4 6 8 10
C 22+1 32+1 42+1 52+1
(1)观察表格,根据规律在表中填空。
(2)用含自然数:n(的代数式表示a,b,c,则 .
(3)猜想:以a,b,c为边的三角形是否为直角三角形 请说明理由.
六、(本题满分12分)
21.在学校组织的研学活动中,辰星小组合作搭建帐篷.如图,这是他们搭建帐篷的支架示意图.在△ABC中,两根支架从帐箋顶点 A 支撑在水平的支架上,一根支架AD⊥BC于点D,另一根支架AE的端点E 在线段BD上,且AE=BE.经测量,知BD=1.6m,AD=1.2m,AC=1.5m .根据测量结果,解答下列问题:
(1)求AE的长.
(2)按照要求,当帐篷支架AB与AC 所夹的角度为直角时,帐篷最为稳定.请通过计算说明辰星小组搭建的帐篷是否符合要求.
七、(本题满分12分)
22.在△ABC中,BC=a,CA=b,AB=c.若∠C为直角,则 若∠C为锐角或钝角,则 与 之间有怎样的大小关系呢 我们一起进行探究吧.
(1)阅读并填空:如图1,若∠C为锐角,则
解:过点A作AD⊥BC于点D,则 BD=BC-CD=a-CD.
在Rt△ABD中, 在Rt△ACD中, ∴ .
即
(2)解答问题:如图2,若 为钝角,试推导与 的大小关系.
八、(本题满分14分)
23.如图,在中, 若点P从点A 出发以的速度沿折线 运动,设运动时间为
(1)若点P在AC上,且满足. 时,求出此时t的值.
(2)若点P恰好在的平分线上(但不与点A重合),求t的值.
第一章:勾股定理单元检测卷答案
一、选择题
1.C 2.B 3.B 4.7 5.16cm2 6.C 7.D 8.A 9.D 10.C
二、填空题
11.300 12.32 13.5 14.或
15.解:在Rt△ABE中,AB2+BE2=62+82=100,∴S=S正方形ABCD-S△ABE=AB2-AE×BE=100-×6×8=76
16.∵ (a-5) +(b-12) +(c-13) =0. 则,a-5=0,b-12=0,c-13=0 ∴a=5,b=12,c=13
2.△ABC是直角三角形 ∵a2+b2=52+122=169=c2 所以△ABC是∠C为直角的直角三角形
17.如图: 连接BD, ∵AB=AD,∠A=60°, ∴△ABD是等边三角形, ∴∠CDB=150°-60°=90°, △BCD是直角三角形, 于是BC+CD=42-12-12=18,从而CD=18-x, 利用勾股定理列方程得(18-BC)2+122=BC2, 解得BC=13.
解答:解:(1)如图所示: (2)S四边形ABCD=6×4=24.
解:(1)△ABE是等腰直角三角形, 证明:∵Rt△ABC绕其锐角顶点A旋转90°得到在Rt△ADE, ∴∠BAC=∠DAE, ∴∠BAE=∠BAC+∠CAE=∠CAE+∠DAE=90°, 又∵AB=AE, ∴△ABE是等腰直角三角形; (2)∵四边形ABFE的面积等于正方形ACFD面积, ∴四边形ABFE的面积等于:b 2. (3)∵S正方形ACFD=S△BAE+S△BFE 即:b2=c2+(b+a)(b﹣a), 整理:2b2=c2+(b+a)(b﹣a) ∴a2+b2=c2.
解:(1)由图表可以得出: ∵n=2时,a=22-1,b=4,c=22+1, n=3时,a=32-1,b=2×3,c=32+1, n=4时,a=42-1,b=2×4,c=42+1, … ∴a=n2-1,b=2n,c=n2+1. (2)a、b、c为边的三角形时: ∵a2+b2=(n2-1)2+4n2=n4+2n2+1, c2=(n2+1)2=n4+2n2+1, ∴a2+b2=c2, ∴以a、b、c为边的三角形是直角三角形. (3)由分析得出:第7组的式子为:112+602=612.
解:在Rt△ABD中,BD=1.6m,AD=1.2m,所以AB==√(1.6 +1.2 )=2m。在Rt△ADC中,AD=1.2m,AC=1.5m,所以CD==0.9m。因此,BC=BD+CD=2.5m。由于AB +AC =2 +1.5 =6.25,BC =2.5 =6.25,所以AB +AC =BC 。因此,△ABC是直角三角形,∠BAC=90°。所以帐篷符合稳定要求.
22.解:(1) AB2= AD2-BD2 , 在△ACD中:AD2=AC2-CD2 AB2-BD2= AC2-CD2 .
(2)证明:过B作BD⊥AC,交AC的延长线于D.设CD为y,则有BD2=a2-y2, 根据勾股定理,得(b+y)2+a2-y2=c2. 即a2+b2+2by=c2.∵b>0,y>0,∴2by>0,∴a2+b2<c2.
23.(1)当t=3时,AP=2×3=6(cm),△ABP的面积=AP×BC=×6×15=45(cm2); 故答案为:45cm2;(2)作PD⊥AB于D,如图所示:∵在△ABC中,∠C=90°,AC=20cm,BC=15cm,∴AB=(cm), ∵AP平分∠CAB, ∴PD=PC=2t-20(cm),AD=AC=20cm, ∴BD=AB-AD=5cm, ∴PB=BC-PC=15-(2t-20)=35-2t(cm), 在Rt△PBD中,由勾股定理得:BD2+PD2=PB2, 即52+(2t-20)2=(35-2t)2, 解得:t=, ∴当t为时,AP平分∠CAB.
(时间:120分钟 满分:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列四组数,是勾股数的是 ( )
A.0.3,0.4,0.5 B.3,4,5 C.6,7,8 D.32,42,52
2.在 Rt△ABC中,∠C=90°,已知a:b=3:4,c=100,其中a,b,c分别为∠A,∠B,∠C的对边,则b的长为 ( )
A.30 B.60 C.80 D.120
3.下列说法中,正确的是 ( )
A.若(c+a)(c-a)=b2,则△ABC是直角三角形
B.若三角形是直角三角形,三角形的三边为a,b,c,则有
C.以三个连续自然数为三边长一定能构成直角三角形
D.在△ABC中,若∠A:∠B:∠C=3:4:5,则△ABC是直角三角形
4.如图,在△ABC中,AB=AC,AB=5,BC=8,AD 是∠BAC的平分线,则AD的长为 ( )
A.6 B.5 C.4 D.3
5.如图,一块边长24米的正方形绿地四周被小路环绕,点B在正方形的边上,BC=7米,则居民从A→C→B 比从A沿直线AB直接到B处要多走 ( )
A.5米 B.25 米 C.12米 D.6米
6.在单位长度为1的正方形网格中,下面的三角形是直角三角形的是 ( )
7.如图,在中,AD平分交BC于点D, ,则点D到AB的距离是 ( )
A.3 B.4 C.5 D.6
8.某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动.如图,当张角为∠BAF时,顶部边缘B 处离桌面的高度BC为7cm,此时底部边缘A处与C处间的距离AC为24 cm,小组成员调整张角的大小继续探究,最后发现当张角为∠DAF时(点D是点B的对应点),顶部边缘D处到桌面的距离 DE 为20cm,则底部边缘A处与 E之间的距离AE为( )
A.15 cm B.18 cm C.21 cm D.24 cm
9.将正方形①②③按如图所示的方式放置,若正方形①②的面积分别是81和144,则正方形③的边长为 ( )
A.225 B.63 C.50 D.15
10.如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高12 cm,在容器内壁离容器底部4cm 的点B 处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,且离容器上沿4cm 的点A处.若蚂蚁吃到蜂蜜需爬行的最短路径为15cm,则该圆柱底面周长为 ( )
A.9 cm B.10 cm C.18 cm D.20cm
二、填空题(本大题共4 小题,每小题5分,满分 20分)
11.如图,船工欲将一艘船横渡一条河,由于水流的影响,实际上岸地点G偏离欲到达点F400m,结果他在水中实际划500m,则该河流的宽度 EF= m.
12.如图,CD⊥AD于点D,AD=12,AC=13.若在直线CD上取一点 B,使AB=15,则△ABC的周长为 .
13.如图,在△ABC中,AB=2,AC=3,AD⊥BC于点 D,E为AD 上任一点,则 .
14.如图,正方形ABCD的面积为144,H是边DC 上的一个动点,将正方形沿过点H的直线GH折叠(点G在边AB上).
(1)若 则 .
(2)若点D的对应点E 恰好落在边BC上的三等分点处,则线段 DH 的长是 .
三、(本大题共2小题,每小题8分,满分16分)
15.如图,点E在正方形ABCD内, 8.试求出阴影部分的面积S.
16.若a,b,c 是 的三边长,且a,b,c 满足
(1)求a,b,c的值.
(2)△ABC是直角三角形吗 请说明理由.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,四边形ABCD的周长为42, 是等边三角形, ,求 BC的长.
18.如图,在边长为1的小正方形组成的网格中,点A,B,C都在格点上,请按要求完成下列各题.
.
(2)若△ABC是直角三角形,且边BC的长为5,请在图中确定点C的位置,并补全△ABC.
五、(本大题共2小题,每小题 10分,满分20分)
19.如图,将任意的 Rt△BAC 绕其锐角顶点 A 逆时针旋转90°得到△EAD,则∠BAE=90°,连接BE,延长 BC,DE交于点 F,则四边形ACFD是一个正方形,且它的面积与四边形ABFE的面积相等.四边形 ABFE的面积等于Rt△BAE与Rt△BFE的面积之和.根据图形写出一种验证勾股定理的方法.
20.在一次“探究性学习”课中,老师设计如下数表:
n 2 3 4 5 6
a 22—1 32—1 42—1 52—1
b 4 6 8 10
C 22+1 32+1 42+1 52+1
(1)观察表格,根据规律在表中填空。
(2)用含自然数:n(的代数式表示a,b,c,则 .
(3)猜想:以a,b,c为边的三角形是否为直角三角形 请说明理由.
六、(本题满分12分)
21.在学校组织的研学活动中,辰星小组合作搭建帐篷.如图,这是他们搭建帐篷的支架示意图.在△ABC中,两根支架从帐箋顶点 A 支撑在水平的支架上,一根支架AD⊥BC于点D,另一根支架AE的端点E 在线段BD上,且AE=BE.经测量,知BD=1.6m,AD=1.2m,AC=1.5m .根据测量结果,解答下列问题:
(1)求AE的长.
(2)按照要求,当帐篷支架AB与AC 所夹的角度为直角时,帐篷最为稳定.请通过计算说明辰星小组搭建的帐篷是否符合要求.
七、(本题满分12分)
22.在△ABC中,BC=a,CA=b,AB=c.若∠C为直角,则 若∠C为锐角或钝角,则 与 之间有怎样的大小关系呢 我们一起进行探究吧.
(1)阅读并填空:如图1,若∠C为锐角,则
解:过点A作AD⊥BC于点D,则 BD=BC-CD=a-CD.
在Rt△ABD中, 在Rt△ACD中, ∴ .
即
(2)解答问题:如图2,若 为钝角,试推导与 的大小关系.
八、(本题满分14分)
23.如图,在中, 若点P从点A 出发以的速度沿折线 运动,设运动时间为
(1)若点P在AC上,且满足. 时,求出此时t的值.
(2)若点P恰好在的平分线上(但不与点A重合),求t的值.
第一章:勾股定理单元检测卷答案
一、选择题
1.C 2.B 3.B 4.7 5.16cm2 6.C 7.D 8.A 9.D 10.C
二、填空题
11.300 12.32 13.5 14.或
15.解:在Rt△ABE中,AB2+BE2=62+82=100,∴S=S正方形ABCD-S△ABE=AB2-AE×BE=100-×6×8=76
16.∵ (a-5) +(b-12) +(c-13) =0. 则,a-5=0,b-12=0,c-13=0 ∴a=5,b=12,c=13
2.△ABC是直角三角形 ∵a2+b2=52+122=169=c2 所以△ABC是∠C为直角的直角三角形
17.如图: 连接BD, ∵AB=AD,∠A=60°, ∴△ABD是等边三角形, ∴∠CDB=150°-60°=90°, △BCD是直角三角形, 于是BC+CD=42-12-12=18,从而CD=18-x, 利用勾股定理列方程得(18-BC)2+122=BC2, 解得BC=13.
解答:解:(1)如图所示: (2)S四边形ABCD=6×4=24.
解:(1)△ABE是等腰直角三角形, 证明:∵Rt△ABC绕其锐角顶点A旋转90°得到在Rt△ADE, ∴∠BAC=∠DAE, ∴∠BAE=∠BAC+∠CAE=∠CAE+∠DAE=90°, 又∵AB=AE, ∴△ABE是等腰直角三角形; (2)∵四边形ABFE的面积等于正方形ACFD面积, ∴四边形ABFE的面积等于:b 2. (3)∵S正方形ACFD=S△BAE+S△BFE 即:b2=c2+(b+a)(b﹣a), 整理:2b2=c2+(b+a)(b﹣a) ∴a2+b2=c2.
解:(1)由图表可以得出: ∵n=2时,a=22-1,b=4,c=22+1, n=3时,a=32-1,b=2×3,c=32+1, n=4时,a=42-1,b=2×4,c=42+1, … ∴a=n2-1,b=2n,c=n2+1. (2)a、b、c为边的三角形时: ∵a2+b2=(n2-1)2+4n2=n4+2n2+1, c2=(n2+1)2=n4+2n2+1, ∴a2+b2=c2, ∴以a、b、c为边的三角形是直角三角形. (3)由分析得出:第7组的式子为:112+602=612.
解:在Rt△ABD中,BD=1.6m,AD=1.2m,所以AB==√(1.6 +1.2 )=2m。在Rt△ADC中,AD=1.2m,AC=1.5m,所以CD==0.9m。因此,BC=BD+CD=2.5m。由于AB +AC =2 +1.5 =6.25,BC =2.5 =6.25,所以AB +AC =BC 。因此,△ABC是直角三角形,∠BAC=90°。所以帐篷符合稳定要求.
22.解:(1) AB2= AD2-BD2 , 在△ACD中:AD2=AC2-CD2 AB2-BD2= AC2-CD2 .
(2)证明:过B作BD⊥AC,交AC的延长线于D.设CD为y,则有BD2=a2-y2, 根据勾股定理,得(b+y)2+a2-y2=c2. 即a2+b2+2by=c2.∵b>0,y>0,∴2by>0,∴a2+b2<c2.
23.(1)当t=3时,AP=2×3=6(cm),△ABP的面积=AP×BC=×6×15=45(cm2); 故答案为:45cm2;(2)作PD⊥AB于D,如图所示:∵在△ABC中,∠C=90°,AC=20cm,BC=15cm,∴AB=(cm), ∵AP平分∠CAB, ∴PD=PC=2t-20(cm),AD=AC=20cm, ∴BD=AB-AD=5cm, ∴PB=BC-PC=15-(2t-20)=35-2t(cm), 在Rt△PBD中,由勾股定理得:BD2+PD2=PB2, 即52+(2t-20)2=(35-2t)2, 解得:t=, ∴当t为时,AP平分∠CAB.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
