2024-2025学年上海师大附中闵行分校、宝山分校联考高三(上)期中数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年上海师大附中闵行分校、宝山分校联考高三(上)期中数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 52.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-18 00:00:00 | ||
图片预览



文档简介
2024-2025学年上海师大附中闵行分校、宝山分校联考高三(上)期中数学试卷
一、单选题:本题共4小题,共18分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知等差数列的公差为,前项和为,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
2.重复次成功概率为的伯努利试验,其成功次数的分布为( )
A. 伯努利分布 B. 二项分布 C. 超几何分布 D. 正态分布
3.以抛物线的焦点为右焦点,且长轴为的椭圆的标准方程为( )
A. B. C. D.
4.已知定义在集合上的函数满足,记的最小值为,最大值为,,,则下列命题正确的是注:表示集合中元素的个数.
A. 若,则 B. 若,则
C. 若,则 D. 若,则
二、填空题:本题共12小题,共54分。
5.已知集合,集合,则 ______.
6.向量在向量方向上的投影为______.
7.二项式的二项展开式中第项的二项式系数为______.
8.复数的共轭复数为______.
9.函数的圆频率是______.
10.已知是定义在上的偶函数,且它在上单调递增,那么使得成立的实数的取值范围是______.
11.四名男生和两名女生排成一排,男生有且只有两位相邻,则不同排法的种数是______结果用数字作答
12.已知,若,,则______.
13.已知,,且,,,则_______
14.设函数在区间恰有三个极值点、两个零点,则的取值范围是 .
15.若直线是曲线的切线,且,则实数的最小值是______.
16.勒洛四面体是一个非常神奇的“四面体”,它能在两个平行平面间自由转动,并且始终保持与两平面都接触,因此它能像球一样来回滚动勒洛四面体是以正四面体的四个顶点为球心,以正四面体的棱长为半径的四个球的公共部分,如图所示,若正四面体的棱长为,则勒洛四面体的体积的取值范围是______.
三、解答题:本题共4小题,共64分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
如图,在长方体中,,,点在上,.
求证:;
求二面角的余弦值.
18.本小题分
十三届全国人大四次会议表决通过了关于“十四五”规划和年远景目标纲要的决议,纲要指出:“加强原创性引领性科技攻关”某企业集中科研骨干,攻克系列“卡脖子”技术,该企业使用新技术对某款芯片进行试生产,该款芯片的性能以某项指标值为衡量标准,性能指标的等级划分如表:
性能指标值
等级
为了解该款芯片的生产效益,该企业从试生产的产品中随机抽样并测量了每件产品的指标值,以组距为画频率分布直方图设,当时为正整数,满足:.
试确定的所有取值,并求;
从样本性能指标值不小于的产品中采用分层随机抽样的方法抽取件产品,然后从这件产品中一次性随机抽取件产品,并求出件都是等级的概率.
19.本小题分
设有椭圆方程,直线:,下端点为,左、右焦点分别为、、,在上.
若中点在轴上,求点的坐标;
直线与轴交于,直线经过右焦点,且,求;
在椭圆上存在一点到距离为,使,当变化时,求的最小值.
20.本小题分
已知函数,若其定义域为,且满足对一切恒成立,则称为一个“逆构造函数”.
设,判断是否为“逆构造函数”,并说明理由;
若函数是“逆构造函数”,求的取值范围;
已知“逆构造函数”满足对任意的,,都有,且求证:对任意,关于的方程无解.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.或
11.
12.
13.
14.
15.
16.
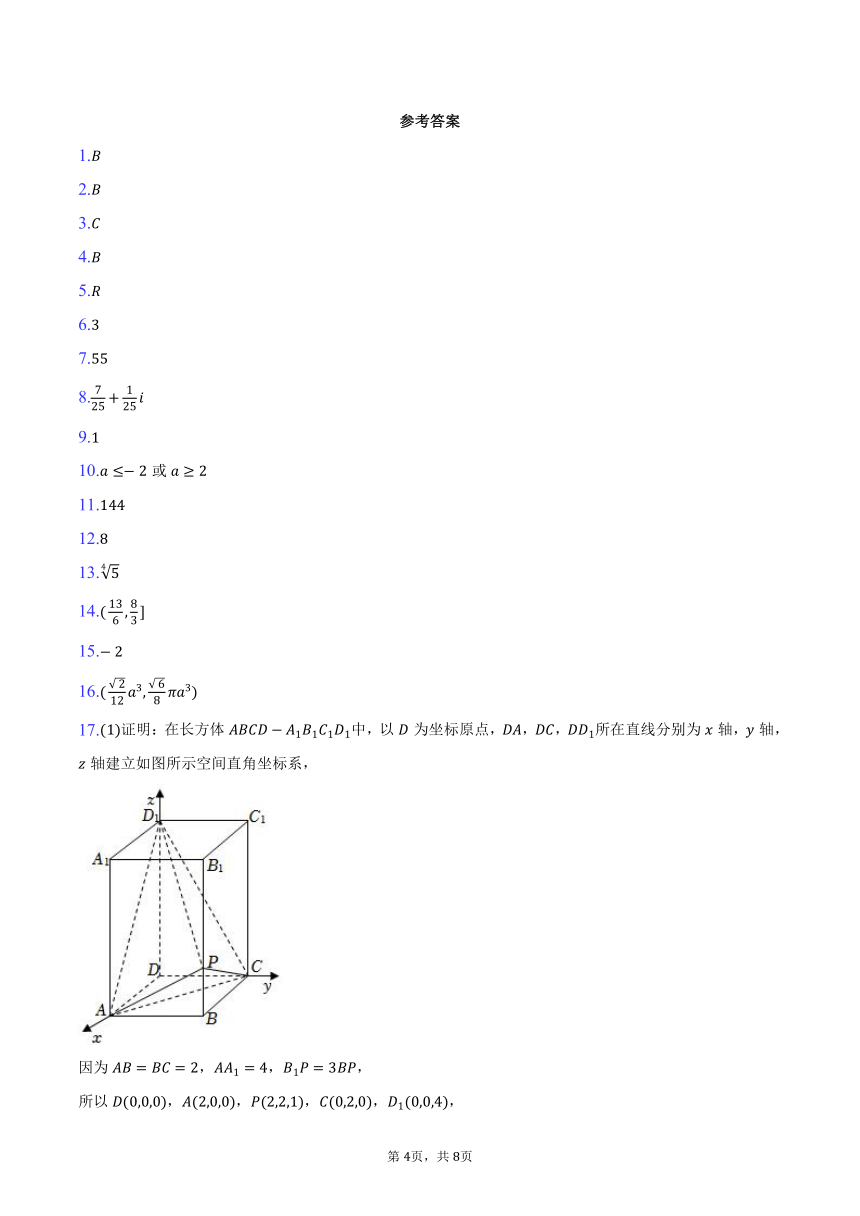
17.证明:在长方体中,以为坐标原点,,,所在直线分别为轴,轴,轴建立如图所示空间直角坐标系,
因为,,,
所以,,,,,
则,
所以有,则
由知,
设平面的一个法向量为,
则,令,则,,
则,
设平面一个法向量为,
,令,则,,
则,
所以,
由图知二面角为锐二面角,
所以二面角的余弦值为.
18.解:根据题意,,按组距为可分成个区间,
分别是,,,,,
,由,,
得的取值集合为,
每个小区间对应的频率值为,
的取值集合为,
,
解得;
等级产品的频率为,等级产品的频率为,
等级产品与等级产品的频率炎比为:,
从样本性能指标值不小于的产品中采用分层抽样的方法抽取件产品,
等级产品的件数为,等级产品的件数为,
从样本性能指标值不小于的产品中采用分层随机抽样的方法抽取件产品,
等级产品的件数为,分别记为,,,,
等级产品的件数为,记为.
从这件产品中任意抽取件产品,所有的可能情况有:
,,,,,
,,,,,共种.
事件“抽取的件产品都是等级”包含的可能情况有:
,,,,,,共种,
故所求概率为.
19.解:由题意可得,,则,
:,,
的中点在轴上,的纵坐标为,
代入,得;
由直线方程可知,
,,
,,
,得,则.
即,,即;
设,由点到直线距离公式可得,
由题意可得椭圆在直线的左下方,则,
即,,
,可得,
由,整理可得,即,
从而.
即的最小值为.
20.解:由于,故对有,
所以是否为“逆构造函数”.
由于,
故,
一方面,若函数是“逆构造函数”,
则,即,
所以对任意成立,
特别地,取,得,
从而,故,
再取,得,
从而,
此即,故,解得;
另一方面,若,则,
设,则,
所以对,有,对有,
从而在上递减,在上递增,
故,
所以对,有,
从而此时函数是“逆构造函数”,
综上,的取值范围是.
证明:设,
则,
所以在上单调递增,
一方面,对,有,
所以对任意,有;
另一方面,对,假设,则根据及零点存在定理,存在使得,
再由条件,知,矛盾,
所以对任意,有.
假设存在,使得,
则根据及零点存在定理,存在使得,从而对任意,有,
但由,知,矛盾,
所以对任意,都有,
综合两方面可知,对任意的,都有,
所以对任意,关于的方程一定无解.
第1页,共1页
一、单选题:本题共4小题,共18分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知等差数列的公差为,前项和为,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
2.重复次成功概率为的伯努利试验,其成功次数的分布为( )
A. 伯努利分布 B. 二项分布 C. 超几何分布 D. 正态分布
3.以抛物线的焦点为右焦点,且长轴为的椭圆的标准方程为( )
A. B. C. D.
4.已知定义在集合上的函数满足,记的最小值为,最大值为,,,则下列命题正确的是注:表示集合中元素的个数.
A. 若,则 B. 若,则
C. 若,则 D. 若,则
二、填空题:本题共12小题,共54分。
5.已知集合,集合,则 ______.
6.向量在向量方向上的投影为______.
7.二项式的二项展开式中第项的二项式系数为______.
8.复数的共轭复数为______.
9.函数的圆频率是______.
10.已知是定义在上的偶函数,且它在上单调递增,那么使得成立的实数的取值范围是______.
11.四名男生和两名女生排成一排,男生有且只有两位相邻,则不同排法的种数是______结果用数字作答
12.已知,若,,则______.
13.已知,,且,,,则_______
14.设函数在区间恰有三个极值点、两个零点,则的取值范围是 .
15.若直线是曲线的切线,且,则实数的最小值是______.
16.勒洛四面体是一个非常神奇的“四面体”,它能在两个平行平面间自由转动,并且始终保持与两平面都接触,因此它能像球一样来回滚动勒洛四面体是以正四面体的四个顶点为球心,以正四面体的棱长为半径的四个球的公共部分,如图所示,若正四面体的棱长为,则勒洛四面体的体积的取值范围是______.
三、解答题:本题共4小题,共64分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
如图,在长方体中,,,点在上,.
求证:;
求二面角的余弦值.
18.本小题分
十三届全国人大四次会议表决通过了关于“十四五”规划和年远景目标纲要的决议,纲要指出:“加强原创性引领性科技攻关”某企业集中科研骨干,攻克系列“卡脖子”技术,该企业使用新技术对某款芯片进行试生产,该款芯片的性能以某项指标值为衡量标准,性能指标的等级划分如表:
性能指标值
等级
为了解该款芯片的生产效益,该企业从试生产的产品中随机抽样并测量了每件产品的指标值,以组距为画频率分布直方图设,当时为正整数,满足:.
试确定的所有取值,并求;
从样本性能指标值不小于的产品中采用分层随机抽样的方法抽取件产品,然后从这件产品中一次性随机抽取件产品,并求出件都是等级的概率.
19.本小题分
设有椭圆方程,直线:,下端点为,左、右焦点分别为、、,在上.
若中点在轴上,求点的坐标;
直线与轴交于,直线经过右焦点,且,求;
在椭圆上存在一点到距离为,使,当变化时,求的最小值.
20.本小题分
已知函数,若其定义域为,且满足对一切恒成立,则称为一个“逆构造函数”.
设,判断是否为“逆构造函数”,并说明理由;
若函数是“逆构造函数”,求的取值范围;
已知“逆构造函数”满足对任意的,,都有,且求证:对任意,关于的方程无解.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.或
11.
12.
13.
14.
15.
16.
17.证明:在长方体中,以为坐标原点,,,所在直线分别为轴,轴,轴建立如图所示空间直角坐标系,
因为,,,
所以,,,,,
则,
所以有,则
由知,
设平面的一个法向量为,
则,令,则,,
则,
设平面一个法向量为,
,令,则,,
则,
所以,
由图知二面角为锐二面角,
所以二面角的余弦值为.
18.解:根据题意,,按组距为可分成个区间,
分别是,,,,,
,由,,
得的取值集合为,
每个小区间对应的频率值为,
的取值集合为,
,
解得;
等级产品的频率为,等级产品的频率为,
等级产品与等级产品的频率炎比为:,
从样本性能指标值不小于的产品中采用分层抽样的方法抽取件产品,
等级产品的件数为,等级产品的件数为,
从样本性能指标值不小于的产品中采用分层随机抽样的方法抽取件产品,
等级产品的件数为,分别记为,,,,
等级产品的件数为,记为.
从这件产品中任意抽取件产品,所有的可能情况有:
,,,,,
,,,,,共种.
事件“抽取的件产品都是等级”包含的可能情况有:
,,,,,,共种,
故所求概率为.
19.解:由题意可得,,则,
:,,
的中点在轴上,的纵坐标为,
代入,得;
由直线方程可知,
,,
,,
,得,则.
即,,即;
设,由点到直线距离公式可得,
由题意可得椭圆在直线的左下方,则,
即,,
,可得,
由,整理可得,即,
从而.
即的最小值为.
20.解:由于,故对有,
所以是否为“逆构造函数”.
由于,
故,
一方面,若函数是“逆构造函数”,
则,即,
所以对任意成立,
特别地,取,得,
从而,故,
再取,得,
从而,
此即,故,解得;
另一方面,若,则,
设,则,
所以对,有,对有,
从而在上递减,在上递增,
故,
所以对,有,
从而此时函数是“逆构造函数”,
综上,的取值范围是.
证明:设,
则,
所以在上单调递增,
一方面,对,有,
所以对任意,有;
另一方面,对,假设,则根据及零点存在定理,存在使得,
再由条件,知,矛盾,
所以对任意,有.
假设存在,使得,
则根据及零点存在定理,存在使得,从而对任意,有,
但由,知,矛盾,
所以对任意,都有,
综合两方面可知,对任意的,都有,
所以对任意,关于的方程一定无解.
第1页,共1页
同课章节目录
