2016春八年级下册数学(沪科版)同步教学课件:19.3.3正方形(共22张PPT)
文档属性
| 名称 | 2016春八年级下册数学(沪科版)同步教学课件:19.3.3正方形(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-20 11:50:58 | ||
图片预览




文档简介
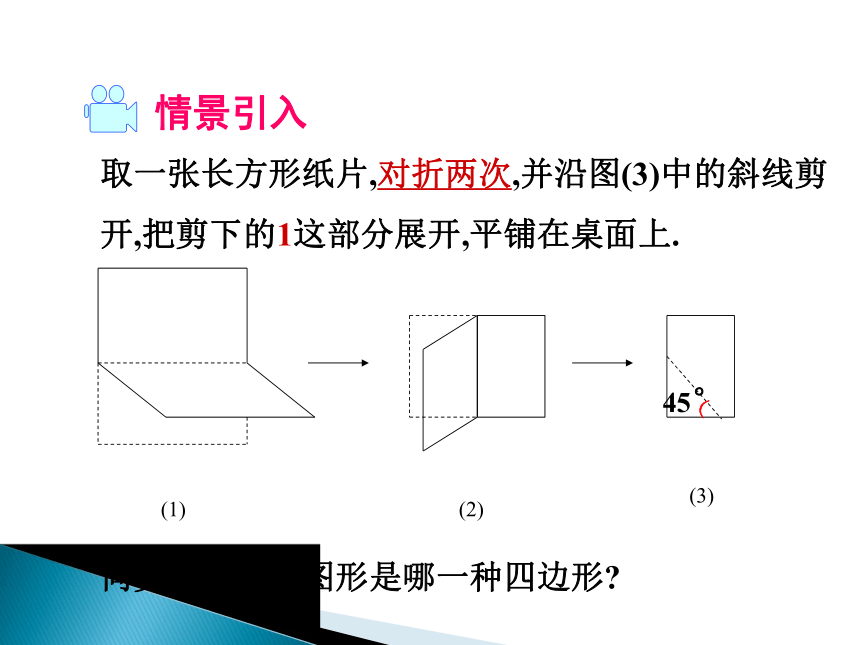
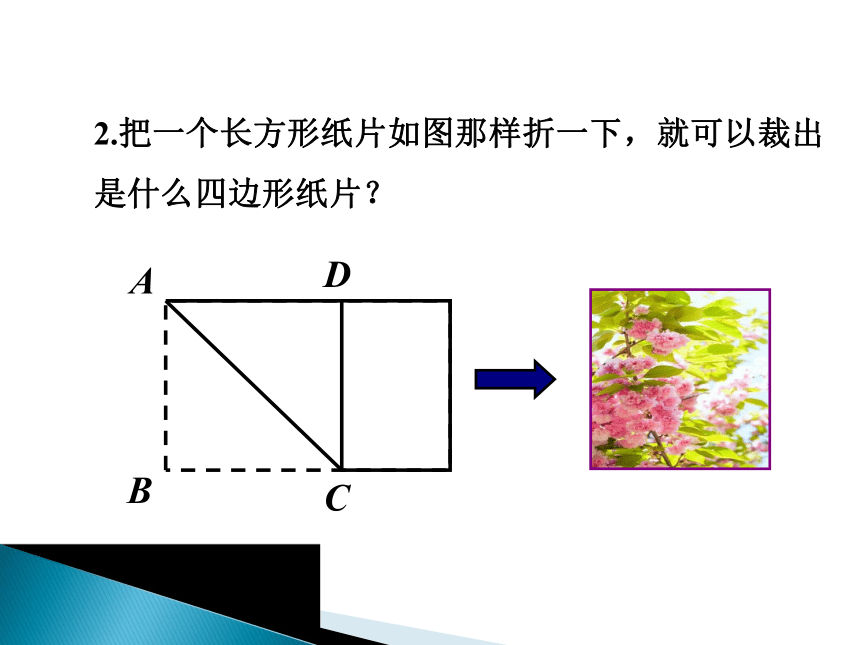
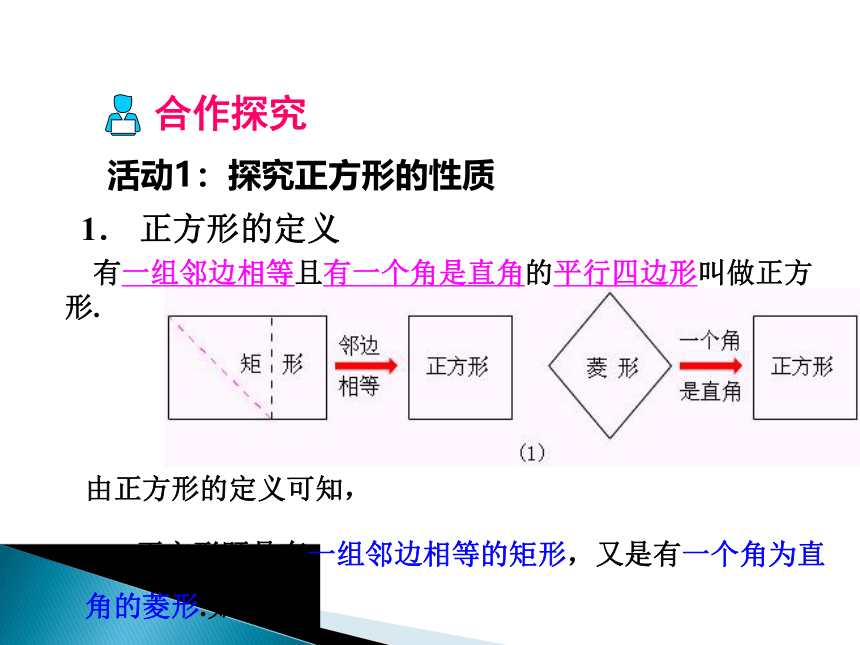
课件22张PPT。19.3 矩形、菱形、正方形3.正方形取一张长方形纸片,对折两次,并沿图(3)中的斜线剪开,把剪下的1这部分展开,平铺在桌面上.(1)(2)(3)问剪出的这个图形是哪一种四边形?情景引入2.把一个长方形纸片如图那样折一下,就可以裁出是什么四边形纸片?正方形就在身边勾股定理1. 正方形的定义由正方形的定义可知,
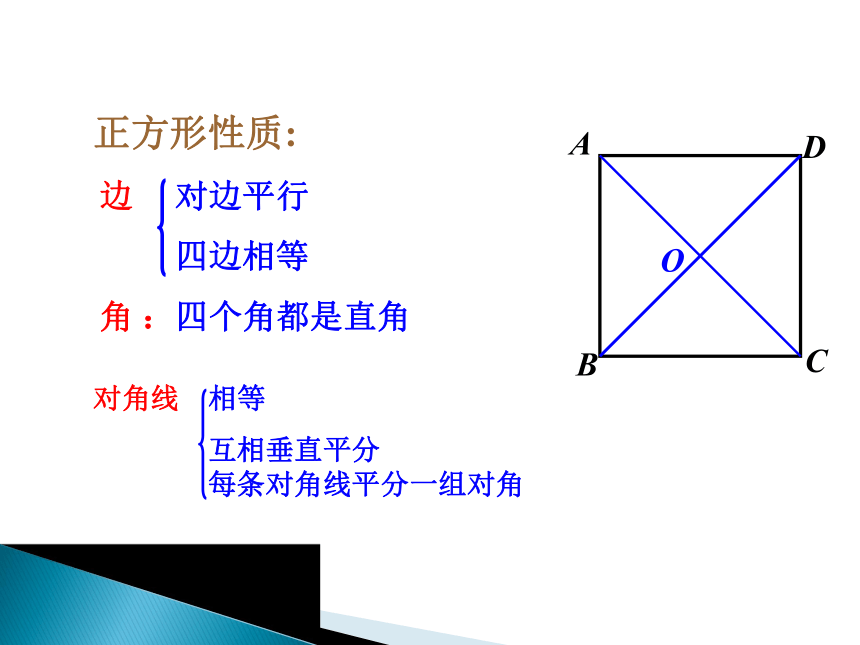
正方形既是有一组邻边相等的矩形,又是有一个角为直角的菱形.如图(1). 有一组邻边相等且有一个角是直角的平行四边形叫做正方形.活动1:探究正方形的性质合作探究 正方形性质:
边 对边平行
四边相等
角 :四个角都是直角对角线 相等
互相垂直平分
每条对角线平分一组对角
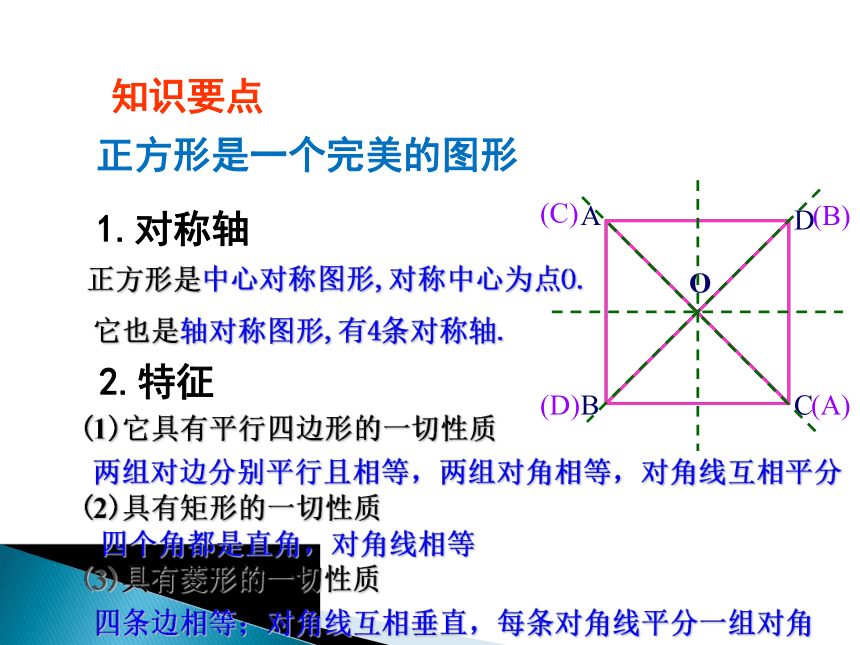
ABDCO 正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.正方形的性质=正方形是中心对称图形,对称中心为点O.它也是轴对称图形,有4条对称轴.(1)它具有平行四边形的一切性质两组对边分别平行且相等,两组对角相等,对角线互相平分(2)具有矩形的一切性质四个角都是直角,对角线相等(3)具有菱形的一切性质四条边相等;对角线互相垂直,每条对角线平分一组对角(A)(B)(C)(D)知识要点2.特征1.对称轴正方形是一个完美的图形从图中可看出,
⑴在正方形中产生了哪些特殊图形?
⑵产生了哪些特殊角?4个全等的小等腰直角三角形和4个全等的大等腰直角三角形.900和450 正方形图形“庐山真面目”例1(1)已知:正方形ABCD对角线AC、BD相交于点O,且AB=2cm,如右图.则AC=_______cm,面积S=________cm2.4(2)正方形ABCD的面积是9cm2.则AB=_______,AC=___________.3cmABDCO例2 如图在正方形ABCD中,E在BC上,BE=2,CE=1,P在BD上,则PE和PC的长度之和最小可达到_____________ .提示由于正方形是轴对称图形,对角线BD是它的对称轴,点A与点C是对称点,因此AE的长就是PE和PC长度和的最小值. 怎样判定一个矩形是正方形?怎样判定一个菱形是正方形?
怎样判定一个平行四边形是正方形? 活动2:探究正方形的判定 1 .定义法:2.矩形法:4.对角线法:你能总结出正方形有哪些判定方法吗?一邻边相等一个直角++平行四边形=正方形3.菱形法:一邻边相等+矩形=正方形一个直角+菱形=正方形互相平分+互相垂直相等+=正方形例3 满足下列条件的四边形是不是正方形?为什么?(1)对角线互相垂直且相等的平行四边形;
(2)对角线互相垂直的矩形;
(3)对角线相等的菱形;
(4)对角线互相垂直平分且相等的四边形.解:(1) 是正方形,根据平行四边形判定法;(2) 是正方形,根据矩形判定法. (3) 是正方形,根据菱形判定法.(4) 是正方形,根据上述其中一个判定方法皆可.例4 下列三个图形都是正方形,你相信吗? 有一组邻边相等并且有一个角是直角的平行四边形是正方形. 既是菱形又是矩形的四边形是正方形. 两条对角线互相垂直平分且相等的四边形是正方形.例5 已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.
求证:四边形CFDE是正方形.提示即用矩形法.即先证四边形CFDE是矩形;
再证DF=DE .例5 已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.
求证:四边形CFDE是正方形.证明:∵∠C=90°,DE⊥BC于E,
DF⊥AC于F
∴四边形CEDF有三个直角,
它是矩形
又∵CD平分∠ACB
根据角平分线上的点都两边的距离相等,可知DE=DF,所以矩形CEDF有一组邻边相等
根据正方形的判定方法,知四边形CEDF是正方形想一想:你能用另外一种方法完成证明吗?思考:正方形与平行四边形、矩形、菱形之间的关系有怎样的包含关系?请填入下图中.菱形正方形矩形一个角是直角 1.正方形的概念: 有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.一组邻边相等 一组邻边相等 一个角是直角 有一组邻边相等有一个角是直角图示:课堂小结 正方形具有_____的性质,同时又具有______的性质.边:对边________,四边_________;
角:四个角都是________;
线:对角线相等,互相________,每条对角线平分一组________.
形:是_______________对称图形.菱形矩形直角都相等相等轴对称和中心平分对角2.正方形的性质:5种识
别方法三个角是直角四条边相等一个角是直角或对角线相等一组邻边相等或对角线垂直一组邻边相等或对角线垂直一个角是直角或对角线相等一个角是直角且一组邻边相等3.平行四边形、矩形、菱形、正方形的判定小结
正方形既是有一组邻边相等的矩形,又是有一个角为直角的菱形.如图(1). 有一组邻边相等且有一个角是直角的平行四边形叫做正方形.活动1:探究正方形的性质合作探究 正方形性质:
边 对边平行
四边相等
角 :四个角都是直角对角线 相等
互相垂直平分
每条对角线平分一组对角
ABDCO 正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.正方形的性质=正方形是中心对称图形,对称中心为点O.它也是轴对称图形,有4条对称轴.(1)它具有平行四边形的一切性质两组对边分别平行且相等,两组对角相等,对角线互相平分(2)具有矩形的一切性质四个角都是直角,对角线相等(3)具有菱形的一切性质四条边相等;对角线互相垂直,每条对角线平分一组对角(A)(B)(C)(D)知识要点2.特征1.对称轴正方形是一个完美的图形从图中可看出,
⑴在正方形中产生了哪些特殊图形?
⑵产生了哪些特殊角?4个全等的小等腰直角三角形和4个全等的大等腰直角三角形.900和450 正方形图形“庐山真面目”例1(1)已知:正方形ABCD对角线AC、BD相交于点O,且AB=2cm,如右图.则AC=_______cm,面积S=________cm2.4(2)正方形ABCD的面积是9cm2.则AB=_______,AC=___________.3cmABDCO例2 如图在正方形ABCD中,E在BC上,BE=2,CE=1,P在BD上,则PE和PC的长度之和最小可达到_____________ .提示由于正方形是轴对称图形,对角线BD是它的对称轴,点A与点C是对称点,因此AE的长就是PE和PC长度和的最小值. 怎样判定一个矩形是正方形?怎样判定一个菱形是正方形?
怎样判定一个平行四边形是正方形? 活动2:探究正方形的判定 1 .定义法:2.矩形法:4.对角线法:你能总结出正方形有哪些判定方法吗?一邻边相等一个直角++平行四边形=正方形3.菱形法:一邻边相等+矩形=正方形一个直角+菱形=正方形互相平分+互相垂直相等+=正方形例3 满足下列条件的四边形是不是正方形?为什么?(1)对角线互相垂直且相等的平行四边形;
(2)对角线互相垂直的矩形;
(3)对角线相等的菱形;
(4)对角线互相垂直平分且相等的四边形.解:(1) 是正方形,根据平行四边形判定法;(2) 是正方形,根据矩形判定法. (3) 是正方形,根据菱形判定法.(4) 是正方形,根据上述其中一个判定方法皆可.例4 下列三个图形都是正方形,你相信吗? 有一组邻边相等并且有一个角是直角的平行四边形是正方形. 既是菱形又是矩形的四边形是正方形. 两条对角线互相垂直平分且相等的四边形是正方形.例5 已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.
求证:四边形CFDE是正方形.提示即用矩形法.即先证四边形CFDE是矩形;
再证DF=DE .例5 已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.
求证:四边形CFDE是正方形.证明:∵∠C=90°,DE⊥BC于E,
DF⊥AC于F
∴四边形CEDF有三个直角,
它是矩形
又∵CD平分∠ACB
根据角平分线上的点都两边的距离相等,可知DE=DF,所以矩形CEDF有一组邻边相等
根据正方形的判定方法,知四边形CEDF是正方形想一想:你能用另外一种方法完成证明吗?思考:正方形与平行四边形、矩形、菱形之间的关系有怎样的包含关系?请填入下图中.菱形正方形矩形一个角是直角 1.正方形的概念: 有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.一组邻边相等 一组邻边相等 一个角是直角 有一组邻边相等有一个角是直角图示:课堂小结 正方形具有_____的性质,同时又具有______的性质.边:对边________,四边_________;
角:四个角都是________;
线:对角线相等,互相________,每条对角线平分一组________.
形:是_______________对称图形.菱形矩形直角都相等相等轴对称和中心平分对角2.正方形的性质:5种识
别方法三个角是直角四条边相等一个角是直角或对角线相等一组邻边相等或对角线垂直一组邻边相等或对角线垂直一个角是直角或对角线相等一个角是直角且一组邻边相等3.平行四边形、矩形、菱形、正方形的判定小结
