2016春八年级下册数学(沪科版)同步教学课件:第20数据的初步分析复习(共22张PPT)
文档属性
| 名称 | 2016春八年级下册数学(沪科版)同步教学课件:第20数据的初步分析复习(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-20 08:02:01 | ||
图片预览







文档简介
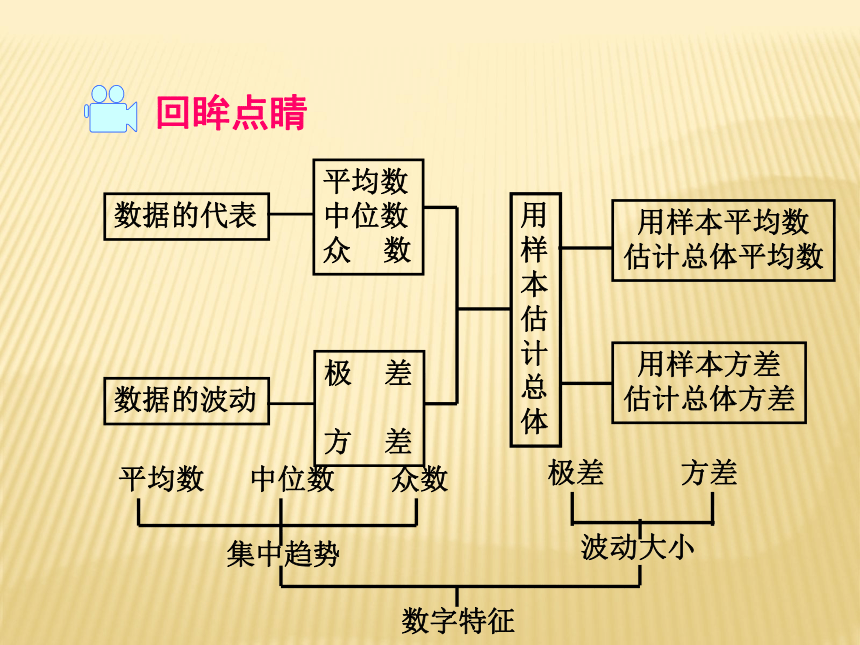
课件22张PPT。小结和复习第20章 数据的初步分析数据的代表平均数
中位数
众 数数据的波动极 差
方 差用
样
本
估
计
总
体用样本平均数
估计总体平均数用样本方差
估计总体方差集中趋势波动大小数字特征回眸点睛中间位置的数 两个数据的平均数 最多 最大数据 最小数据 平均数 大 1.统计的基本思想:样本特征估计总体的特征.
2.统计的决策依据:利用数据进行决策时,要全面、多角
度地去分析已有数据,从数据的变化中发现它们的规律
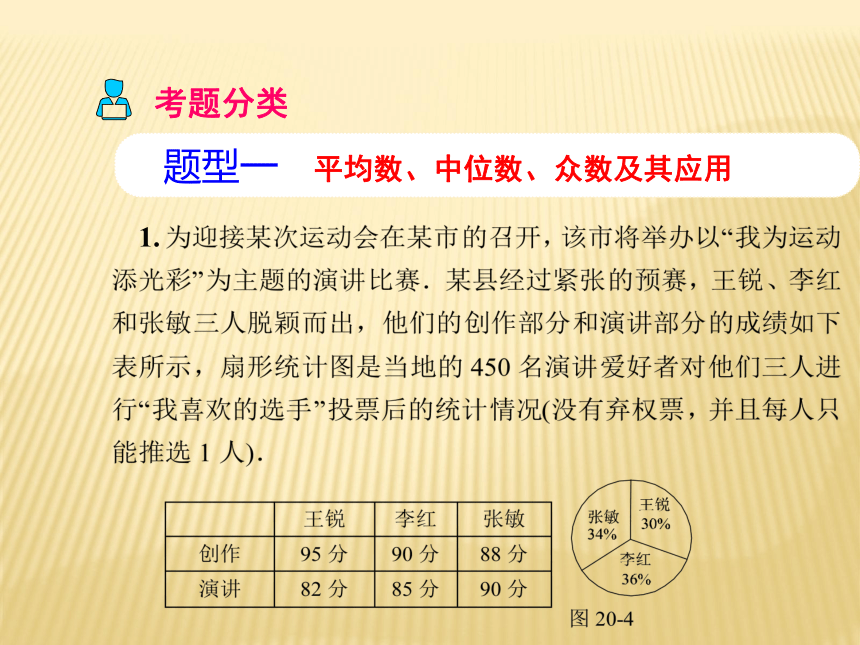
和变化趋势,减少人为因素的影响.用样本估计总体 题型一 平均数、中位数、众数及其应用1.考题分类(1)请计算三位参赛选手的得票数各是多少? (2)现要从王锐、李红和张敏三人中推选一人代表该地区参加全市的决赛,推选方案为:①演讲爱好者所投票,每票记1分;②将创作、演讲、得票三项所得分按4∶5∶1的比例确定个人成绩.请计算三位选手的个人成绩,从他们的个人成绩看,谁将会被推选参加该市的决赛? 2. 2010年因干旱影响,凉山州政府鼓励居民节约用水,为了解居民用水情况,在某小区随机抽查了20户家庭的月用水量,结果如下表:则关于这20户家庭的月用水量,下列说法错误的是( )
A.中位数是6吨 B.平均数是5.8吨
C.众数是6吨 D.极差是4吨变式题 :四个数据8,10,x,10的平均数与中位数相等,则x
等于( )
A.8 B.10 C.12 D.8或12DD1.在某旅游景区上山的一条小路上,有一些断断续续的台阶,如图所示,是其中的甲、乙台阶的示意图,请你用学过的统计知识回答下列问题:151616141415151118171019甲路段乙路段(1)两段台阶路有哪些相同点和不同点?解:相同点:两段台阶的平均高度相同;
不同点:两段台阶的中位数、方差和极差不同.题型二 极差、方差及其应用151616141415151118171019甲路段乙路段(2)哪段台阶路走起来更舒服?为什么? (3)为方便游客行走,需要重新整修上山的小路,对于这两段台阶,在台阶数不变的情况下,请你提出合理的整修建议.解:使每个台阶的高度均为15cm,使得方差为0.解:甲台阶走起来更舒服些,因为它的台阶高度的方差小.题型三 数据分析的应用 1. 2014年7月25日全国青少年校园足球比赛落幕,某学校为了解本校2400名学生对本次足球赛的关注程度,以利于做好教育和引导工作,随机抽取了本校内的六、七、八、九四个年级部分学生进行调查,按“各年级被抽取人数”与“关注程度”,分别绘制了条形统计图(图1-1)、扇形统计图(图1-2)和折线统计图(图2).(1)本次共随机抽查了 名学生,根据信息补全图(1-1)中条形统计图,图(1-2)中八年级所对应扇形的圆心角的度数为 ;200144°补全如图(2)如果把“特别关注”、“一般关注”、“偶尔关注”都看作成关注,那么全校关注足球赛的学生大约有多少名?(2)根据题意得:关注的学生所占的百分比为,
所以全校关注足球赛的学生大约有2400×55%=1320 (人); (3)①根据上面的统计结果,谈谈你对该校学生对足球关注的现状的看法及建议; (3)①根据以上所求可得出:只有55%的学生关注足球,有45%的学生不关注,可以看出仍有部分学生忽略了足球的关注,希望学校做好教育与引导工作,加大对足球进校园的宣传力度,让校园足球得到更多的关注和支持,推动校园足球的发展. (3)②如果要了解学校中小学生校园足球的关注情况,你认为应该如何进行抽样?②考虑到样本具有的随机性、代表性、广泛性,如果要了解中小学生对足球的关注的情况,抽样时应针对不同的年级、不同性别、不同年龄段的学生进行随机抽样. 1.平均数、中位数、众数及其应用2.极差、方差及其应用3.数据分析的应用复习归纳 1.四川雅安发生地震灾害后,某中学九(1)班学生积极捐款献爱心,如图35-3所示是该班50名学生的捐款情况统计,则他们捐款金额的众数和中位数分别是( )
A.20,10 B.10,20
C.16,15 D.15,16B课后演练 2.小张和小李去练习射击,第一轮 10发子弹打完后,两人的成绩如图.根据图中的信息,小张小李两人中成绩较稳定的是 .小张 3.为了解 2012 年全国中学生创新能力大赛中竞赛项目
“知识产权”的笔试情况,随机抽查了部分参赛同学的成绩,
整理并绘制了如下尚不完整的统计表和如图的统计图.请根据以上图表提供的信息,解答下列问题:
(1)本次调查的样本容量为________;
(2)在表中:m=____,n=________ ;
(3)补全频数分布直方图;(4)参加比赛的小聪说,他的比赛成绩是所有抽查同学成绩的中位数,据此推断他的成绩落在________分数段内;300120 0.380≤x<90(5)如果比赛成绩 80 分以上(含 80 分)为优秀,那么你估计该竞赛项目的优秀率大约是________.60%
中位数
众 数数据的波动极 差
方 差用
样
本
估
计
总
体用样本平均数
估计总体平均数用样本方差
估计总体方差集中趋势波动大小数字特征回眸点睛中间位置的数 两个数据的平均数 最多 最大数据 最小数据 平均数 大 1.统计的基本思想:样本特征估计总体的特征.
2.统计的决策依据:利用数据进行决策时,要全面、多角
度地去分析已有数据,从数据的变化中发现它们的规律
和变化趋势,减少人为因素的影响.用样本估计总体 题型一 平均数、中位数、众数及其应用1.考题分类(1)请计算三位参赛选手的得票数各是多少? (2)现要从王锐、李红和张敏三人中推选一人代表该地区参加全市的决赛,推选方案为:①演讲爱好者所投票,每票记1分;②将创作、演讲、得票三项所得分按4∶5∶1的比例确定个人成绩.请计算三位选手的个人成绩,从他们的个人成绩看,谁将会被推选参加该市的决赛? 2. 2010年因干旱影响,凉山州政府鼓励居民节约用水,为了解居民用水情况,在某小区随机抽查了20户家庭的月用水量,结果如下表:则关于这20户家庭的月用水量,下列说法错误的是( )
A.中位数是6吨 B.平均数是5.8吨
C.众数是6吨 D.极差是4吨变式题 :四个数据8,10,x,10的平均数与中位数相等,则x
等于( )
A.8 B.10 C.12 D.8或12DD1.在某旅游景区上山的一条小路上,有一些断断续续的台阶,如图所示,是其中的甲、乙台阶的示意图,请你用学过的统计知识回答下列问题:151616141415151118171019甲路段乙路段(1)两段台阶路有哪些相同点和不同点?解:相同点:两段台阶的平均高度相同;
不同点:两段台阶的中位数、方差和极差不同.题型二 极差、方差及其应用151616141415151118171019甲路段乙路段(2)哪段台阶路走起来更舒服?为什么? (3)为方便游客行走,需要重新整修上山的小路,对于这两段台阶,在台阶数不变的情况下,请你提出合理的整修建议.解:使每个台阶的高度均为15cm,使得方差为0.解:甲台阶走起来更舒服些,因为它的台阶高度的方差小.题型三 数据分析的应用 1. 2014年7月25日全国青少年校园足球比赛落幕,某学校为了解本校2400名学生对本次足球赛的关注程度,以利于做好教育和引导工作,随机抽取了本校内的六、七、八、九四个年级部分学生进行调查,按“各年级被抽取人数”与“关注程度”,分别绘制了条形统计图(图1-1)、扇形统计图(图1-2)和折线统计图(图2).(1)本次共随机抽查了 名学生,根据信息补全图(1-1)中条形统计图,图(1-2)中八年级所对应扇形的圆心角的度数为 ;200144°补全如图(2)如果把“特别关注”、“一般关注”、“偶尔关注”都看作成关注,那么全校关注足球赛的学生大约有多少名?(2)根据题意得:关注的学生所占的百分比为,
所以全校关注足球赛的学生大约有2400×55%=1320 (人); (3)①根据上面的统计结果,谈谈你对该校学生对足球关注的现状的看法及建议; (3)①根据以上所求可得出:只有55%的学生关注足球,有45%的学生不关注,可以看出仍有部分学生忽略了足球的关注,希望学校做好教育与引导工作,加大对足球进校园的宣传力度,让校园足球得到更多的关注和支持,推动校园足球的发展. (3)②如果要了解学校中小学生校园足球的关注情况,你认为应该如何进行抽样?②考虑到样本具有的随机性、代表性、广泛性,如果要了解中小学生对足球的关注的情况,抽样时应针对不同的年级、不同性别、不同年龄段的学生进行随机抽样. 1.平均数、中位数、众数及其应用2.极差、方差及其应用3.数据分析的应用复习归纳 1.四川雅安发生地震灾害后,某中学九(1)班学生积极捐款献爱心,如图35-3所示是该班50名学生的捐款情况统计,则他们捐款金额的众数和中位数分别是( )
A.20,10 B.10,20
C.16,15 D.15,16B课后演练 2.小张和小李去练习射击,第一轮 10发子弹打完后,两人的成绩如图.根据图中的信息,小张小李两人中成绩较稳定的是 .小张 3.为了解 2012 年全国中学生创新能力大赛中竞赛项目
“知识产权”的笔试情况,随机抽查了部分参赛同学的成绩,
整理并绘制了如下尚不完整的统计表和如图的统计图.请根据以上图表提供的信息,解答下列问题:
(1)本次调查的样本容量为________;
(2)在表中:m=____,n=________ ;
(3)补全频数分布直方图;(4)参加比赛的小聪说,他的比赛成绩是所有抽查同学成绩的中位数,据此推断他的成绩落在________分数段内;300120 0.380≤x<90(5)如果比赛成绩 80 分以上(含 80 分)为优秀,那么你估计该竞赛项目的优秀率大约是________.60%
