北师大版数学八年级下册 第一章三角形的证明 综合测试卷(含答案)
文档属性
| 名称 | 北师大版数学八年级下册 第一章三角形的证明 综合测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-19 11:25:15 | ||
图片预览


文档简介
第一章综合测试卷
时间:120 分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题4分,共40分)
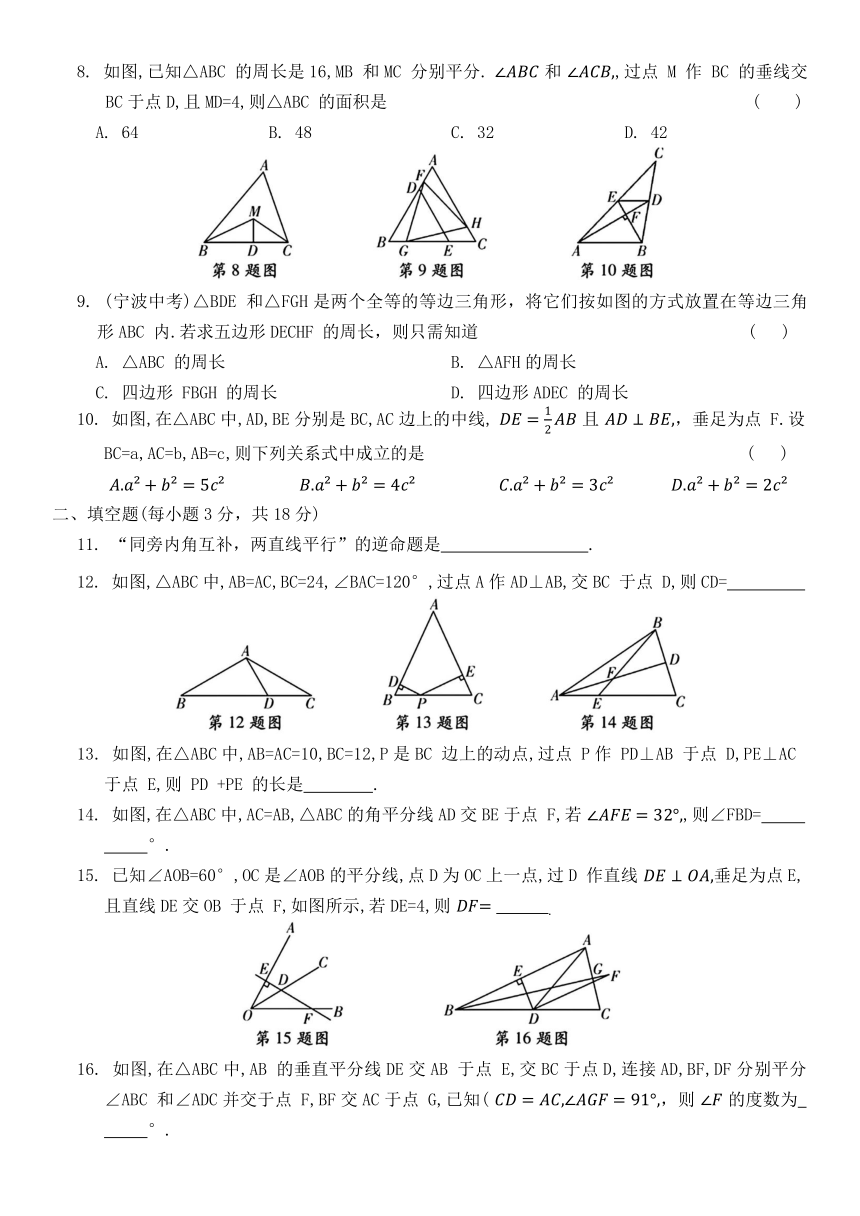
1. 等腰三角形的一个内角是70°,则它顶角的度数是 ( )
A. 70° B. 70°或40° C. 70°或50° D. 40°
2. 如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O.如果AB=AC,那么图中全等的直角三角形的对数是 ( )
A. 1 B. 2 C. 3 D. 4
3. 如图,已知∠AOB=10°,且OC=CD=DE=EF=FG=GH,则∠BGH= ( )
A. 50° B. 60° C. 70° D. 80°
4. 如图,OD平分∠AOB,DE⊥AO于点E,DE=4,点F是射线OB上的任意一点,则DF的长度不可能是 ( )
A. 3 B. 4 C. 5 D. 6
5. 如图,是5×5的正方形方格图,点A,B在小方格的顶点上,要在小方格的顶点中确定一点C,连接AC和BC,使△ABC是等腰三角形,则方格图中满足条件的点C的个数是 ( )
A. 4 B. 5 C. 6 D. 7
6. 如图,在等腰△ABC中,AB=AC=10,BC=12,O是△ABC外一点,O到三边的垂线段分别为OD,OE,OF,且OD:OE:OF=1:4:4,则AO的长度为 ( )
A. 10 B. 9
7. 如图,在△ABC中,∠BAC=80°,AB 边的垂直平分线交AB 于点 D,交 BC于点 E,AC 边的垂直平分线交AC于点 F,交 BC 于点 G,连接AE,AG.则∠EAG的度数为 ( )
A. 15° B. 20° C. 25° D. 30°
8. 如图,已知△ABC 的周长是16,MB 和MC 分别平分. 和 ,过点 M 作 BC 的垂线交 BC于点D,且MD=4,则△ABC 的面积是 ( )
A. 64 B. 48 C. 32 D. 42
9. (宁波中考)△BDE 和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC 内.若求五边形DECHF 的周长,则只需知道 ( )
A. △ABC 的周长 B. △AFH的周长
C. 四边形 FBGH 的周长 D. 四边形ADEC 的周长
10. 如图,在△ABC中,AD,BE分别是BC,AC边上的中线, 且 ,垂足为点 F.设BC=a,AC=b,AB=c,则下列关系式中成立的是 ( )
二、填空题(每小题3分,共18分)
11. “同旁内角互补,两直线平行”的逆命题是 .
12. 如图,△ABC中,AB=AC,BC=24,∠BAC=120°,过点A作AD⊥AB,交BC 于点 D,则CD=
13. 如图,在△ABC中,AB=AC=10,BC=12,P是BC 边上的动点,过点 P作 PD⊥AB 于点 D,PE⊥AC 于点 E,则 PD +PE 的长是 .
14. 如图,在△ABC中,AC=AB,△ABC的角平分线AD交BE于点 F,若 ,则∠FBD= °.
15. 已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D 作直线 垂足为点E,且直线DE交OB 于点 F,如图所示,若DE=4,则
16. 如图,在△ABC中,AB 的垂直平分线DE交AB 于点 E,交BC于点D,连接AD,BF,DF分别平分∠ABC 和∠ADC并交于点 F,BF交AC于点 G,已知( ,则 的度数为 °.
三、解答题(共62分)
17. (6分)如图,在等腰△ABC中,∠A是顶角,N是边AB上任意一点(不与点A,B重合),过点N作NM⊥AB 于点N,交BC的延长线于点 M,若∠A=30°,求∠NMB 的度数.
18.(6分)如图,四边形ABCD中,∠C=90°,BD平分∠ABC,AD=3,E为AB上一点,AE=4,ED=3,求 CD的长.
19. (9分)如图,在△ABC中,AB=AC=8,AB的垂直平分线交AB于点D,交AC 于点E.
(1)若BE-EC=2,求CE的长.
(2)若∠A=36°,求证:△BEC是等腰三角形.
20. (7分)已知:如图,BP,CP分别是△ABC的外角平分线,PM⊥AB 于点M,PN⊥AC 于点 N.求证:PA平分∠MAN.
21. (10分)如图, 中, ,若点 P从点A 出发以每秒 1 cm的速度向点 C 运动,设运动时间为t秒
(1)若点 P 恰好在 的角平分线上,求出此时t的值.
(2)若点 P 使得. 时,求出此时t的值.
22. (10分)如图,等腰直角三角板如图放置.直角顶点C在直线m上,分别过点A,B作 直线m于点 E, 直线m于点 D.
(1)求证:
(2)若设 三边分别为a,b,c,利用此图证明勾股定理.
23. (14分)已知:在 中, ,点 E在AB 上,以 BE为底边作等腰. ,取 CE 的中点为G,连接AG,DG.
(1)如图1,若. ,求证:
(2)如图2,若 ,则(1)中结论仍然成立吗 说明理由.
第一章综合测试卷
1. B 2. C 3. B 4. A 5. C 6. D 7. B 8. C 9. A 10. A
11. 两直线平行,同旁内角互补12. 8 13. 14. 58 15. 8 16. 13
17. 解:∵
∵MN⊥AB,∴∠BNM=90°,
18. 解:如图,作DH⊥AE于点 H,
在Rt△DAH 中,
∵ BD平分∠ABC,∠C=90°,∴DC=DH=
19. (1)解:∵AB的垂直平分线交AB 于点D,∴EA=EB,
∵BE-EC=2,∴BE=EC+2,
∵AE=AC-EC=8-EC,
∴8-EC=EC+2,∴CE=3.
(2)证明:∵EA=EB,∴∠EBA=∠A=36°,
∴∠BEC=∠A+∠EBA=72°,∵AB=AC,
∴∠C=∠BEC,∴△BEC是等腰三角形.
20. 证明:如图,作 于点 D,∵ BP 是 的外角 的平分线,
,同理,PN=PD,
又∵
∴ PA平分∠MAN.
21. 解:(1)如图,作 PD⊥AB 于点 D,设.AP=t,
∵BP平分∠ABC,∴PC=PD=8-t,
解得t=5.
(2)∵ PB+PC=AC,∴ PB =PA =t,在 Rt△BCP 中, 即 解得
22. 证明:(1)∵∠ACB=90°,∠ACE+∠BCD=90°,∵ ∠ACE+∠CAE=90°,∴∠CAE=∠BCD,在△AEC与△CDB中,
∴△AEC≌△CDB(AAS).∴EC=BD.
(2)由(1)知:BD=CE=a,CD=AE=b,
整理,得
23. (1)证明:如图1,延长 DG至点 H,使GH=GD,连接AD,AH,CH,
∵G为CE的中点,∴GC=GE,在△CHG和△EDG中,
∴△CHG≌△EDG(SAS),
∴CH=ED,∠HCG=∠DEG,
∵BD=ED,∠BDE=120°,∴∠BED=∠EBD=30°,
∵AB=AC,∠BAC=60°,∴△ABC为等边三角形,
∵ AE = BE,∴ CE⊥AB,∴ ∠BED + ∠DEG =90°,∠BAC +∠ACE=90°,
∴∠HCG=∠DEG=60°,∠ACE=30°,
∴∠ACH=30°,∴∠ABD=∠ACH,在△ABD和△ACH中, ∴ △ABD≌△ACH(SAS),∴AD=AH,∵HG=DG,∴AG⊥DG.
(2)解:(1)中结论仍然成立.理由如下:如图2,延长DG至点 M,使GM=GD,连接AD,AM,CM,
∵G为CE的中点,∴GC=GE,在△CMG和△EDG中
∴△CMG≌△EDG(SAS),
∴CM=ED,∠MCG=∠DEG,
∴∠BAC=2∠BED=2∠EBD,
∵∠BEC=∠BED+∠DEG=∠BAC+∠ACE,
∴∠BED+∠MCG=∠BAC+∠ACE,
∵∠MCG=∠ACM+∠ACE,
∴∠BED+∠ACM+∠ACE=2∠BED+∠ACE,
∴∠ACM=∠BED=∠ABD,
在△ABD 和△ACM中,
∴ △ABD≌△ACM(SAS),∴AD=AM,
∵MG=DG,∴AG⊥DG.
时间:120 分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题4分,共40分)
1. 等腰三角形的一个内角是70°,则它顶角的度数是 ( )
A. 70° B. 70°或40° C. 70°或50° D. 40°
2. 如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O.如果AB=AC,那么图中全等的直角三角形的对数是 ( )
A. 1 B. 2 C. 3 D. 4
3. 如图,已知∠AOB=10°,且OC=CD=DE=EF=FG=GH,则∠BGH= ( )
A. 50° B. 60° C. 70° D. 80°
4. 如图,OD平分∠AOB,DE⊥AO于点E,DE=4,点F是射线OB上的任意一点,则DF的长度不可能是 ( )
A. 3 B. 4 C. 5 D. 6
5. 如图,是5×5的正方形方格图,点A,B在小方格的顶点上,要在小方格的顶点中确定一点C,连接AC和BC,使△ABC是等腰三角形,则方格图中满足条件的点C的个数是 ( )
A. 4 B. 5 C. 6 D. 7
6. 如图,在等腰△ABC中,AB=AC=10,BC=12,O是△ABC外一点,O到三边的垂线段分别为OD,OE,OF,且OD:OE:OF=1:4:4,则AO的长度为 ( )
A. 10 B. 9
7. 如图,在△ABC中,∠BAC=80°,AB 边的垂直平分线交AB 于点 D,交 BC于点 E,AC 边的垂直平分线交AC于点 F,交 BC 于点 G,连接AE,AG.则∠EAG的度数为 ( )
A. 15° B. 20° C. 25° D. 30°
8. 如图,已知△ABC 的周长是16,MB 和MC 分别平分. 和 ,过点 M 作 BC 的垂线交 BC于点D,且MD=4,则△ABC 的面积是 ( )
A. 64 B. 48 C. 32 D. 42
9. (宁波中考)△BDE 和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC 内.若求五边形DECHF 的周长,则只需知道 ( )
A. △ABC 的周长 B. △AFH的周长
C. 四边形 FBGH 的周长 D. 四边形ADEC 的周长
10. 如图,在△ABC中,AD,BE分别是BC,AC边上的中线, 且 ,垂足为点 F.设BC=a,AC=b,AB=c,则下列关系式中成立的是 ( )
二、填空题(每小题3分,共18分)
11. “同旁内角互补,两直线平行”的逆命题是 .
12. 如图,△ABC中,AB=AC,BC=24,∠BAC=120°,过点A作AD⊥AB,交BC 于点 D,则CD=
13. 如图,在△ABC中,AB=AC=10,BC=12,P是BC 边上的动点,过点 P作 PD⊥AB 于点 D,PE⊥AC 于点 E,则 PD +PE 的长是 .
14. 如图,在△ABC中,AC=AB,△ABC的角平分线AD交BE于点 F,若 ,则∠FBD= °.
15. 已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D 作直线 垂足为点E,且直线DE交OB 于点 F,如图所示,若DE=4,则
16. 如图,在△ABC中,AB 的垂直平分线DE交AB 于点 E,交BC于点D,连接AD,BF,DF分别平分∠ABC 和∠ADC并交于点 F,BF交AC于点 G,已知( ,则 的度数为 °.
三、解答题(共62分)
17. (6分)如图,在等腰△ABC中,∠A是顶角,N是边AB上任意一点(不与点A,B重合),过点N作NM⊥AB 于点N,交BC的延长线于点 M,若∠A=30°,求∠NMB 的度数.
18.(6分)如图,四边形ABCD中,∠C=90°,BD平分∠ABC,AD=3,E为AB上一点,AE=4,ED=3,求 CD的长.
19. (9分)如图,在△ABC中,AB=AC=8,AB的垂直平分线交AB于点D,交AC 于点E.
(1)若BE-EC=2,求CE的长.
(2)若∠A=36°,求证:△BEC是等腰三角形.
20. (7分)已知:如图,BP,CP分别是△ABC的外角平分线,PM⊥AB 于点M,PN⊥AC 于点 N.求证:PA平分∠MAN.
21. (10分)如图, 中, ,若点 P从点A 出发以每秒 1 cm的速度向点 C 运动,设运动时间为t秒
(1)若点 P 恰好在 的角平分线上,求出此时t的值.
(2)若点 P 使得. 时,求出此时t的值.
22. (10分)如图,等腰直角三角板如图放置.直角顶点C在直线m上,分别过点A,B作 直线m于点 E, 直线m于点 D.
(1)求证:
(2)若设 三边分别为a,b,c,利用此图证明勾股定理.
23. (14分)已知:在 中, ,点 E在AB 上,以 BE为底边作等腰. ,取 CE 的中点为G,连接AG,DG.
(1)如图1,若. ,求证:
(2)如图2,若 ,则(1)中结论仍然成立吗 说明理由.
第一章综合测试卷
1. B 2. C 3. B 4. A 5. C 6. D 7. B 8. C 9. A 10. A
11. 两直线平行,同旁内角互补12. 8 13. 14. 58 15. 8 16. 13
17. 解:∵
∵MN⊥AB,∴∠BNM=90°,
18. 解:如图,作DH⊥AE于点 H,
在Rt△DAH 中,
∵ BD平分∠ABC,∠C=90°,∴DC=DH=
19. (1)解:∵AB的垂直平分线交AB 于点D,∴EA=EB,
∵BE-EC=2,∴BE=EC+2,
∵AE=AC-EC=8-EC,
∴8-EC=EC+2,∴CE=3.
(2)证明:∵EA=EB,∴∠EBA=∠A=36°,
∴∠BEC=∠A+∠EBA=72°,∵AB=AC,
∴∠C=∠BEC,∴△BEC是等腰三角形.
20. 证明:如图,作 于点 D,∵ BP 是 的外角 的平分线,
,同理,PN=PD,
又∵
∴ PA平分∠MAN.
21. 解:(1)如图,作 PD⊥AB 于点 D,设.AP=t,
∵BP平分∠ABC,∴PC=PD=8-t,
解得t=5.
(2)∵ PB+PC=AC,∴ PB =PA =t,在 Rt△BCP 中, 即 解得
22. 证明:(1)∵∠ACB=90°,∠ACE+∠BCD=90°,∵ ∠ACE+∠CAE=90°,∴∠CAE=∠BCD,在△AEC与△CDB中,
∴△AEC≌△CDB(AAS).∴EC=BD.
(2)由(1)知:BD=CE=a,CD=AE=b,
整理,得
23. (1)证明:如图1,延长 DG至点 H,使GH=GD,连接AD,AH,CH,
∵G为CE的中点,∴GC=GE,在△CHG和△EDG中,
∴△CHG≌△EDG(SAS),
∴CH=ED,∠HCG=∠DEG,
∵BD=ED,∠BDE=120°,∴∠BED=∠EBD=30°,
∵AB=AC,∠BAC=60°,∴△ABC为等边三角形,
∵ AE = BE,∴ CE⊥AB,∴ ∠BED + ∠DEG =90°,∠BAC +∠ACE=90°,
∴∠HCG=∠DEG=60°,∠ACE=30°,
∴∠ACH=30°,∴∠ABD=∠ACH,在△ABD和△ACH中, ∴ △ABD≌△ACH(SAS),∴AD=AH,∵HG=DG,∴AG⊥DG.
(2)解:(1)中结论仍然成立.理由如下:如图2,延长DG至点 M,使GM=GD,连接AD,AM,CM,
∵G为CE的中点,∴GC=GE,在△CMG和△EDG中
∴△CMG≌△EDG(SAS),
∴CM=ED,∠MCG=∠DEG,
∴∠BAC=2∠BED=2∠EBD,
∵∠BEC=∠BED+∠DEG=∠BAC+∠ACE,
∴∠BED+∠MCG=∠BAC+∠ACE,
∵∠MCG=∠ACM+∠ACE,
∴∠BED+∠ACM+∠ACE=2∠BED+∠ACE,
∴∠ACM=∠BED=∠ABD,
在△ABD 和△ACM中,
∴ △ABD≌△ACM(SAS),∴AD=AM,
∵MG=DG,∴AG⊥DG.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
