北师大版数学八年级下册 第三章图形的平移与旋转 综合测试卷(含答案)
文档属性
| 名称 | 北师大版数学八年级下册 第三章图形的平移与旋转 综合测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-19 11:32:04 | ||
图片预览

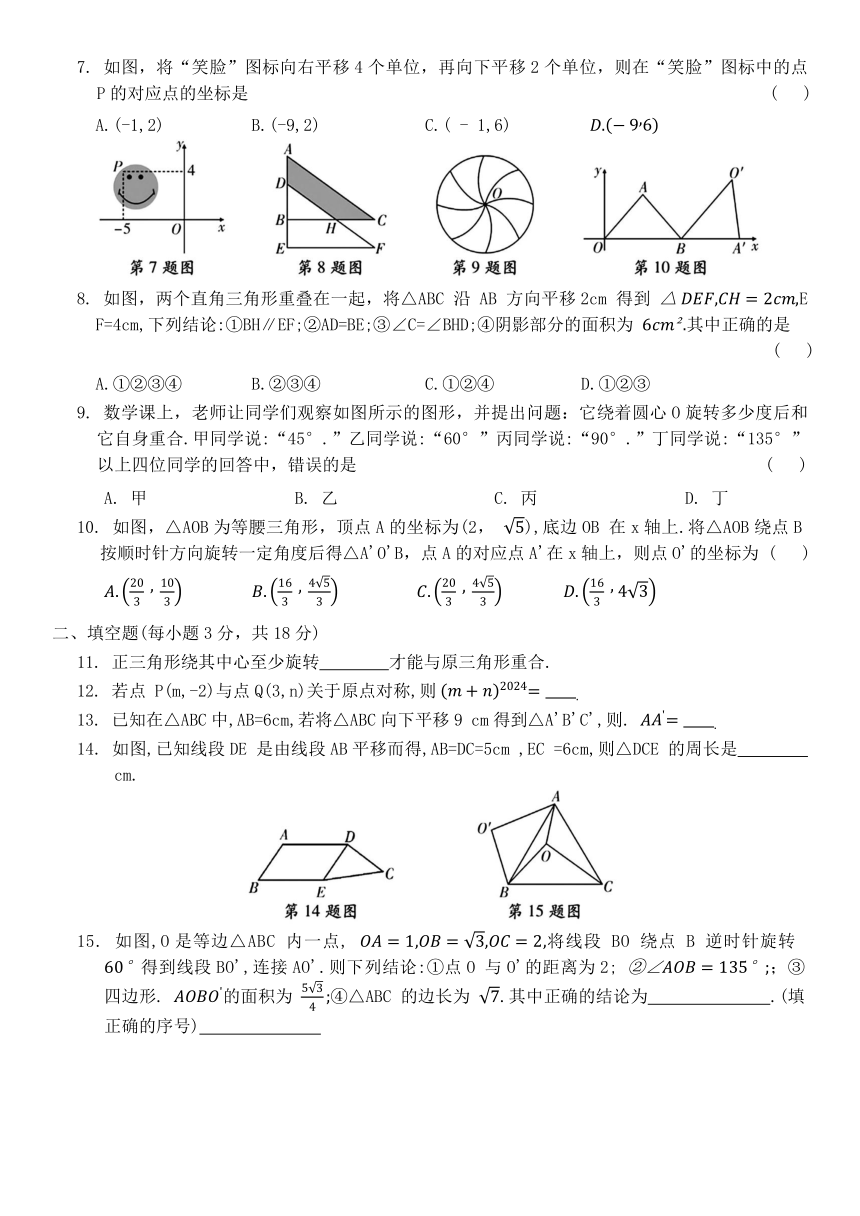

文档简介
第三章图形的平移与旋转综合测试卷
时间:120 分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题5分,共50分)
1. 下列关于防范“新冠肺炎”的标志中既是轴对称图形,又是中心对称图形的是 ( )
2. 下列说法正确的是 ( )
A. 平移前后图形大小可能改变
B. 对应点到旋转中心的距离相等
C. 平移和旋转的共同之处是改变了图形的位置和大小
D. 由旋转得到的图形一定可以通过平移得到
3. 在平面直角坐标系中,将点( -2,3)先向右平移4个单位长度,再向下平移2个单位长度,得到的点的坐标为 ( )
A.(2,1) B.(-6,5) C.(2,5) D.(-6,1)
4. 如图,将△AOB绕着点O顺时针旋转,得到△COD,若∠AOB=40°,∠BOC=25°,则旋转角度是( )
A. 25° B. 15° C. 65° D. 40°
5. 如图,点A 为△ABC与△AB'C'的对称中心,若 则BB'的长为 ( )
A. 2 B. 4 D. 8
6. 如图,在5×5的小正方形网格中,每个小正方形的边长均为1,点A,B,O都在格点上.若将△OAB绕点O逆时针旋转90°,得到△OA'B',A,B 的对应点分别为A',B',则A,B'之间的距离为
( )
B. 5
7. 如图,将“笑脸”图标向右平移4个单位,再向下平移2个单位,则在“笑脸”图标中的点P的对应点的坐标是 ( )
A.(-1,2) B.(-9,2) C.( - 1,6)
8. 如图,两个直角三角形重叠在一起,将△ABC 沿 AB 方向平移2cm 得到 EF=4cm,下列结论:①BH∥EF;②AD=BE;③∠C=∠BHD;④阴影部分的面积为 其中正确的是 ( )
A.①②③④ B.②③④ C.①②④ D.①②③
9. 数学课上,老师让同学们观察如图所示的图形,并提出问题:它绕着圆心O旋转多少度后和它自身重合.甲同学说:“45°.”乙同学说:“60°”丙同学说:“90°.”丁同学说:“135°”以上四位同学的回答中,错误的是 ( )
A. 甲 B. 乙 C. 丙 D. 丁
10. 如图,△AOB为等腰三角形,顶点A的坐标为(2, ),底边OB 在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A'O'B,点A的对应点A'在x轴上,则点O'的坐标为 ( )
二、填空题(每小题3分,共18分)
11. 正三角形绕其中心至少旋转 才能与原三角形重合.
12. 若点 P(m,-2)与点Q(3,n)关于原点对称,则
13. 已知在△ABC中,AB=6cm,若将△ABC向下平移9 cm得到△A'B'C',则.
14. 如图,已知线段DE 是由线段AB平移而得,AB=DC=5cm ,EC =6cm,则△DCE 的周长是 cm.
15. 如图,O是等边△ABC 内一点, 将线段 BO 绕点 B 逆时针旋转 得到线段BO',连接AO'.则下列结论:①点O 与O'的距离为2; ;③四边形. 的面积为 ④△ABC 的边长为 .其中正确的结论为 .(填正确的序号)
16. 如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),( -1,0).一个电动玩具从坐标原点O 出发,第一次跳跃到点. 使得点P 与点O关于点A 成中心对称;第二次跳跃到点 P ,使得点 P 与点 关于点 B 成中心对称;第三次跳跃到点 P ,使得点 P 与点P 关于点 C 成中心对称;第四次跳跃到点 P ,使得点 P 与点 P 关于点A成中心对称;第五次跳跃到点 P ,使得点 P 与点 P 关于点B成中心对称;……,照此规律重复下去,则点 的坐标为 .
三、解答题(共52分)
17. (8分)如图所示,在4×4的方格内,已将其中的2个小正方形涂成黑色,请你分别在图①、图②、图③、图④中再将两个空白的小正方形涂成黑色,使4个黑色小正方形组成一个轴对称图形,画出与示意图不同的4种方案.(每个 的方格内限画一种)
要求:(1)4个黑色小正方形必须相连.(有公共边或公共顶点视为相连)
(2)将选中的小正方形方格用黑色签字笔涂成阴影图形.(若两个方案的图形经过翻折、平移、旋转后能够重合,均视为一种方案)
18. (8分)如图, 是等边三角形,以AD 为边向外作 使 且 2,连接BE,求 BE的长.
19. (8分)如图,在平面直角坐标系中, 三个顶点的坐标分别为 把 先向右平移3个单位长度,再向下平移3个单位长度后得到 且点 的对应点为A,点 的对应点为B,点( 的对应点为 C.
(1)在坐标系中画出.
(2)求 的面积.
(3)设点 P在y轴上,且 与 的面积相等,求点 P 的坐标.
20. (8分)如图,在 中, ,D为BC的中点, ,DE交AB 于点 E,DF交AC 于点 F,试探索线段BE,EF,FC 之间的数量关系.
21. (8分)如图,在平面直角坐标系中,等边三角形OAB 的顶点B 的坐标为(2,0),点A 在第一象限内,将 沿OA方向平移至 的位置,此时点 '的横坐标为3,则点 的坐标为多少
22. (12分)如图,已知 是等边三角形,在 外有一点 D,连接AD,BD,CD,将 绕点A 按顺时针方向旋转得到 AD与BE交于点 F,
(1)求 的大小.
(2)若 ,求AD的长.
第三章图形的平移与旋转综合测试卷
C 2. B 3. A 4. C 5. B6. C7. A 8. A 9. B 10. C11. 120° 12. - 1 13. 9 cm
14. 16 15.③④ 16.(2,2)
17. 解:如图所示:
18. 解:如图,将DE绕点 E 逆时针旋转 得到EF,连接AF,DF,则 ,由旋转的性质,得
是等边三角形,.
是等边三角形,
即 在
中,由勾股定理,得
在 和 中,
19. 解:(1)如图, 即为所求.
(3)设P(0,m),由题意得, 解得m=5或-3,∴P(0,5)或(0,-3).
20. 解: 理由如下:
∵ D 是 BC 的中点,∴ BD = CD,作△CDM,使△CDM 与△BDE 关于点 O成中心对称,如图.
由中心对称性质可得 CM =BE,MD=ED,∠DCM=∠B.
又∵∠B+∠ACB=90°,
∴ ∠DCM+∠ACB=90°,即∠FCM =90°.
连接FM.在△FME中,MD=ED,FD⊥ME,∴FM=FE.
又∵在 Rt△FCM中,
21. 解:如图,过点A 作AM⊥x轴于点 M.∵ B(2,0),△OAB是等边三角形,
∴OA=OB=2,∠AOB=60°,
∴ 直线OA 的函数表达式为 且 时,y= ∴将点 A 向右平移2个单位长度,再向上平移 个单位长度后可得点 设点 的坐标为(m,n),则 即
22. 解:(1)∵将 绕点A 按顺时针方向旋转得到.
(2)如图,连接DE,
是等边三角形,
∵将 绕点 A 按顺时针方向旋转得到
时间:120 分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题5分,共50分)
1. 下列关于防范“新冠肺炎”的标志中既是轴对称图形,又是中心对称图形的是 ( )
2. 下列说法正确的是 ( )
A. 平移前后图形大小可能改变
B. 对应点到旋转中心的距离相等
C. 平移和旋转的共同之处是改变了图形的位置和大小
D. 由旋转得到的图形一定可以通过平移得到
3. 在平面直角坐标系中,将点( -2,3)先向右平移4个单位长度,再向下平移2个单位长度,得到的点的坐标为 ( )
A.(2,1) B.(-6,5) C.(2,5) D.(-6,1)
4. 如图,将△AOB绕着点O顺时针旋转,得到△COD,若∠AOB=40°,∠BOC=25°,则旋转角度是( )
A. 25° B. 15° C. 65° D. 40°
5. 如图,点A 为△ABC与△AB'C'的对称中心,若 则BB'的长为 ( )
A. 2 B. 4 D. 8
6. 如图,在5×5的小正方形网格中,每个小正方形的边长均为1,点A,B,O都在格点上.若将△OAB绕点O逆时针旋转90°,得到△OA'B',A,B 的对应点分别为A',B',则A,B'之间的距离为
( )
B. 5
7. 如图,将“笑脸”图标向右平移4个单位,再向下平移2个单位,则在“笑脸”图标中的点P的对应点的坐标是 ( )
A.(-1,2) B.(-9,2) C.( - 1,6)
8. 如图,两个直角三角形重叠在一起,将△ABC 沿 AB 方向平移2cm 得到 EF=4cm,下列结论:①BH∥EF;②AD=BE;③∠C=∠BHD;④阴影部分的面积为 其中正确的是 ( )
A.①②③④ B.②③④ C.①②④ D.①②③
9. 数学课上,老师让同学们观察如图所示的图形,并提出问题:它绕着圆心O旋转多少度后和它自身重合.甲同学说:“45°.”乙同学说:“60°”丙同学说:“90°.”丁同学说:“135°”以上四位同学的回答中,错误的是 ( )
A. 甲 B. 乙 C. 丙 D. 丁
10. 如图,△AOB为等腰三角形,顶点A的坐标为(2, ),底边OB 在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A'O'B,点A的对应点A'在x轴上,则点O'的坐标为 ( )
二、填空题(每小题3分,共18分)
11. 正三角形绕其中心至少旋转 才能与原三角形重合.
12. 若点 P(m,-2)与点Q(3,n)关于原点对称,则
13. 已知在△ABC中,AB=6cm,若将△ABC向下平移9 cm得到△A'B'C',则.
14. 如图,已知线段DE 是由线段AB平移而得,AB=DC=5cm ,EC =6cm,则△DCE 的周长是 cm.
15. 如图,O是等边△ABC 内一点, 将线段 BO 绕点 B 逆时针旋转 得到线段BO',连接AO'.则下列结论:①点O 与O'的距离为2; ;③四边形. 的面积为 ④△ABC 的边长为 .其中正确的结论为 .(填正确的序号)
16. 如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),( -1,0).一个电动玩具从坐标原点O 出发,第一次跳跃到点. 使得点P 与点O关于点A 成中心对称;第二次跳跃到点 P ,使得点 P 与点 关于点 B 成中心对称;第三次跳跃到点 P ,使得点 P 与点P 关于点 C 成中心对称;第四次跳跃到点 P ,使得点 P 与点 P 关于点A成中心对称;第五次跳跃到点 P ,使得点 P 与点 P 关于点B成中心对称;……,照此规律重复下去,则点 的坐标为 .
三、解答题(共52分)
17. (8分)如图所示,在4×4的方格内,已将其中的2个小正方形涂成黑色,请你分别在图①、图②、图③、图④中再将两个空白的小正方形涂成黑色,使4个黑色小正方形组成一个轴对称图形,画出与示意图不同的4种方案.(每个 的方格内限画一种)
要求:(1)4个黑色小正方形必须相连.(有公共边或公共顶点视为相连)
(2)将选中的小正方形方格用黑色签字笔涂成阴影图形.(若两个方案的图形经过翻折、平移、旋转后能够重合,均视为一种方案)
18. (8分)如图, 是等边三角形,以AD 为边向外作 使 且 2,连接BE,求 BE的长.
19. (8分)如图,在平面直角坐标系中, 三个顶点的坐标分别为 把 先向右平移3个单位长度,再向下平移3个单位长度后得到 且点 的对应点为A,点 的对应点为B,点( 的对应点为 C.
(1)在坐标系中画出.
(2)求 的面积.
(3)设点 P在y轴上,且 与 的面积相等,求点 P 的坐标.
20. (8分)如图,在 中, ,D为BC的中点, ,DE交AB 于点 E,DF交AC 于点 F,试探索线段BE,EF,FC 之间的数量关系.
21. (8分)如图,在平面直角坐标系中,等边三角形OAB 的顶点B 的坐标为(2,0),点A 在第一象限内,将 沿OA方向平移至 的位置,此时点 '的横坐标为3,则点 的坐标为多少
22. (12分)如图,已知 是等边三角形,在 外有一点 D,连接AD,BD,CD,将 绕点A 按顺时针方向旋转得到 AD与BE交于点 F,
(1)求 的大小.
(2)若 ,求AD的长.
第三章图形的平移与旋转综合测试卷
C 2. B 3. A 4. C 5. B6. C7. A 8. A 9. B 10. C11. 120° 12. - 1 13. 9 cm
14. 16 15.③④ 16.(2,2)
17. 解:如图所示:
18. 解:如图,将DE绕点 E 逆时针旋转 得到EF,连接AF,DF,则 ,由旋转的性质,得
是等边三角形,.
是等边三角形,
即 在
中,由勾股定理,得
在 和 中,
19. 解:(1)如图, 即为所求.
(3)设P(0,m),由题意得, 解得m=5或-3,∴P(0,5)或(0,-3).
20. 解: 理由如下:
∵ D 是 BC 的中点,∴ BD = CD,作△CDM,使△CDM 与△BDE 关于点 O成中心对称,如图.
由中心对称性质可得 CM =BE,MD=ED,∠DCM=∠B.
又∵∠B+∠ACB=90°,
∴ ∠DCM+∠ACB=90°,即∠FCM =90°.
连接FM.在△FME中,MD=ED,FD⊥ME,∴FM=FE.
又∵在 Rt△FCM中,
21. 解:如图,过点A 作AM⊥x轴于点 M.∵ B(2,0),△OAB是等边三角形,
∴OA=OB=2,∠AOB=60°,
∴ 直线OA 的函数表达式为 且 时,y= ∴将点 A 向右平移2个单位长度,再向上平移 个单位长度后可得点 设点 的坐标为(m,n),则 即
22. 解:(1)∵将 绕点A 按顺时针方向旋转得到.
(2)如图,连接DE,
是等边三角形,
∵将 绕点 A 按顺时针方向旋转得到
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
