整式的乘法与因式分解 单元训练(一)(含解析)
文档属性
| 名称 | 整式的乘法与因式分解 单元训练(一)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 215.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-18 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
整式的乘法与因式分解 单元训练(一)
一.选择题(共6小题,满分18分,每小题3分)
1.(3分)下列运算正确的是( )
A.x6+x6=2x12
B.(﹣2a2b)3=﹣8a8b3
C.[﹣(m﹣n)3]2=[﹣(m﹣n)2]3
D.(﹣y4) (﹣y)6÷(﹣y)7=y3
2.(3分)若6x=3,6y=16,则6x﹣y的值为( )
A. B.﹣13 C. D.19
3.(3分)下列各式能用平方差公式计算的是( )
A.(a﹣b)(b﹣a) B.(a+b)(b+a)
C.(a﹣b)(﹣a﹣b) D.(a+b)(﹣a﹣b)
4.(3分)若a+b=3,ab=﹣12,则a2﹣ab+b2的值为( )
A.57 B.21 C.45 D.33
5.(3分)在运用乘法公式计算(2x﹣y+3)(2x+y﹣3)时,下列变形正确的是( )
A.[(2x﹣y)+3][(2x+y)﹣3] B.[(2x﹣y)+3][(2x﹣y)﹣3]
C.[2x﹣(y+3)][2x+(y﹣3)] D.[2x﹣(y﹣3)][2x+(y﹣3)]
6.(3分)下列整式中不含有x+1这个因式的是( )
A.x2﹣1 B.x4﹣x3+x2﹣1
C.x3+1 D.x4﹣x3﹣x2﹣1
二.填空题(共6小题,满分18分,每小题3分)
7.(3分)当x满足x 时,(x﹣3)0有意义.
8.(3分)若xa=3,x2a﹣3b,则xb的值为 .
9.(3分)关于x的多项式(x+1)(3x﹣n)展开合并后一次项系数为﹣1,则n的值为 .
10.(3分)设a为正整数,且满足a2+2a+40是完全平方数,则a的值是 .
11.(3分)如果(m、n都是常数),那么n的值是 .
12.(3分)若一个四位正整数满足:a+c=b+d,我们就称该数是“交替数”,则最小的“交替数”是 ;若一个“交替数”m满足千位数字与百位数字的平方差是15,且十位数字与个位数的和能被5整除.则满足条件的“交替数”m的最大值为 .
三.解答题(共11小题,满分84分)
13.(6分)(1)2x2 (x﹣1)+x3;
(2)(x2﹣2)(x+3)﹣x(x2+2x﹣1).
14.(6分)已知3a=4,3b=10,3c=16.
(1)求3a+b的值;
(2)求32a﹣c的值.
15.(6分)(1)已知a2﹣a﹣5=0,求(4﹣a)(3+a)的值.
(2)已知a2+a﹣5=0,求(a2﹣5)(a+1)的值.
16.(6分)利用乘法公式计算:
(1)(2+1)(22+1)(24+1);
(2)1002﹣992+982﹣972+…+22﹣12.
17.(6分)用简便方法计算:
(1);
(2)222﹣2×44+4.
18.(8分)因式分解:
(1)x2﹣12xy+36y2;
(2)3a2﹣27;
(3)6x(y2﹣2)﹣2x(2y2+3);
(4)4(a﹣b)x2﹣8xy(a﹣b)+4y2(a﹣b).
19.(8分)已知xy=15,且满足(x2y﹣xy2)﹣(x﹣y)=28.
(1)求x﹣y的值;
(2)求x2+y2,x+y的值.
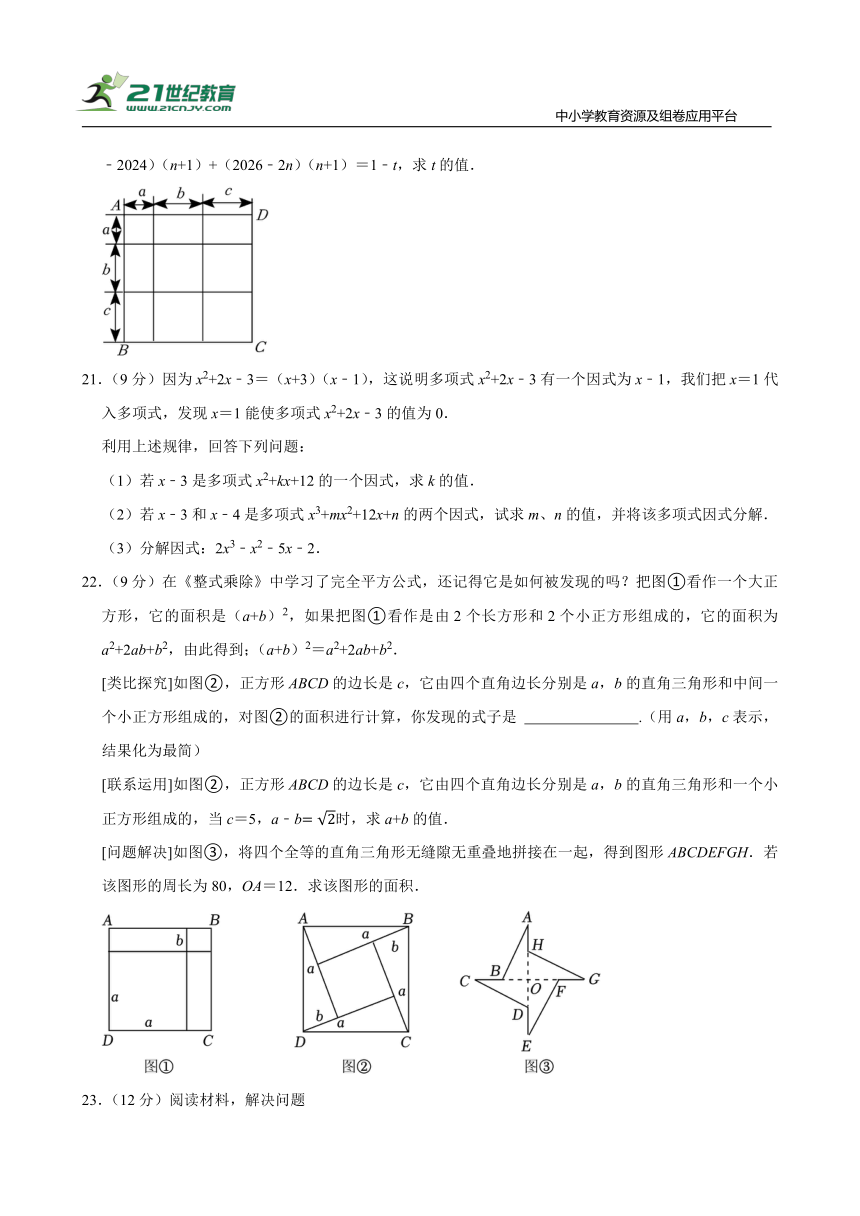
20.(8分)我们知道,利用图形的面积能解释与得出代数恒等式,请你解答下列问题:
(1)如图,根据3个正方形和6个长方形的面积之和等于大正方形ABCD的面积.可以得到代数恒等式:(a+b+c)2= ;
(2)若n、t满足:(n﹣2024)2+(2026﹣2n)2+(n+1)2=t2+2t﹣18,(n﹣2024)(2026﹣2n)+(n﹣2024)(n+1)+(2026﹣2n)(n+1)=1﹣t,求t的值.
21.(9分)因为x2+2x﹣3=(x+3)(x﹣1),这说明多项式x2+2x﹣3有一个因式为x﹣1,我们把x=1代入多项式,发现x=1能使多项式x2+2x﹣3的值为0.
利用上述规律,回答下列问题:
(1)若x﹣3是多项式x2+kx+12的一个因式,求k的值.
(2)若x﹣3和x﹣4是多项式x3+mx2+12x+n的两个因式,试求m、n的值,并将该多项式因式分解.
(3)分解因式:2x3﹣x2﹣5x﹣2.
22.(9分)在《整式乘除》中学习了完全平方公式,还记得它是如何被发现的吗?把图①看作一个大正方形,它的面积是(a+b)2,如果把图①看作是由2个长方形和2个小正方形组成的,它的面积为a2+2ab+b2,由此得到;(a+b)2=a2+2ab+b2.
[类比探究]如图②,正方形ABCD的边长是c,它由四个直角边长分别是a,b的直角三角形和中间一个小正方形组成的,对图②的面积进行计算,你发现的式子是 .(用a,b,c表示,结果化为最简)
[联系运用]如图②,正方形ABCD的边长是c,它由四个直角边长分别是a,b的直角三角形和一个小正方形组成的,当c=5,a﹣b时,求a+b的值.
[问题解决]如图③,将四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形ABCDEFGH.若该图形的周长为80,OA=12.求该图形的面积.
23.(12分)阅读材料,解决问题
【材料1】将形如x2+px+q的二次三项式因式分解时,如果能满足q=mn且p=m+n,则可以把x2+px+q因式分解成(x+m)(x+n).
如,x2+4x+3中,常数项3=1×3,一次项系数4=1+3,∴x2+4x+3=(x+1)(x+3);同理,x2﹣4x﹣12中,常数项“﹣12”=﹣6×2,一次项系数“﹣4”=﹣6+2,
∴x2﹣4x﹣12=(x﹣6)(x+2).
【材料2】因式分解:(x+y)2+2(x+y)+1
解:把x+y看成一个整体,令x+y=A,则
原式=A2+2A+1=(A+1)2,再将A=x+y重新代入,得:原式=(x+y+1)2.
上述解题用到的“整体思想”是数学解题中常见的思想方法.请你解答下列问题:
(1)根据材料1,因式分解x2﹣6x+8;
(2)结合材料1和材料2,完成下面小题:
①分解因式:(x﹣y)2+4(x﹣y)+3;
②分解因式:m(m+2)(m2+2m﹣2)﹣3.
整式的乘法与因式分解 单元训练(一)
一.选择题(共6小题,满分18分,每小题3分)
1.(3分)下列运算正确的是( )
A.x6+x6=2x12
B.(﹣2a2b)3=﹣8a8b3
C.[﹣(m﹣n)3]2=[﹣(m﹣n)2]3
D.(﹣y4) (﹣y)6÷(﹣y)7=y3
【思路点拔】根据同底数幂的乘除法法则、幂的乘方与积的乘方法则、合并同类项的方法进行解题即可.
【解答】解:A、x6+x6=2x6,故该项不正确,不符合题意;
B、(﹣2a2b)3=﹣8a6b3,故该项不正确,不符合题意;
C、[﹣(m﹣n)3]2=(m﹣n)6,[﹣(m﹣n)2]3=﹣(m﹣n)6,两者不相等,故该项不正确,不符合题意;
D、(﹣y4) (﹣y)6÷(﹣y)7=﹣y10÷(﹣y)7=y3,故该项正确,符合题意;
故选:D.
2.(3分)若6x=3,6y=16,则6x﹣y的值为( )
A. B.﹣13 C. D.19
【思路点拔】根据同底数幂的除法法则进行计算,即可解答.
【解答】解:∵6x=3,6y=16,
∴6x﹣y=6x÷6y=3÷16,
故选:A.
3.(3分)下列各式能用平方差公式计算的是( )
A.(a﹣b)(b﹣a) B.(a+b)(b+a)
C.(a﹣b)(﹣a﹣b) D.(a+b)(﹣a﹣b)
【思路点拔】根据平方差公式、完全平方公式的结构特征逐项判断即可.
【解答】解:A、(a﹣b)(b﹣a)=﹣(a﹣b)(a﹣b)=﹣(a﹣b)2=﹣(a2﹣2ab+b2)=﹣a2+2ab﹣b2,不能用平方差公式计算,故此选项不符合题意;
B、(a+b)(b+a)=(a+b)(a+b)=(a+b)2=a2+2ab+b2,不能用平方差公式计算,故此选项不符合题意;
C、(a﹣b)(﹣a﹣b)=﹣(a﹣b)(a+b)=﹣(a2﹣b2)=﹣a2+b2,能用平方差公式计算,故此选项符合题意;
D、(a+b)(﹣a﹣b)=﹣(a+b)(a+b)﹣(a+b)2=﹣(a2+2ab+b2)=﹣a2﹣2ab﹣b2,不能用平方差公式计算,故此选项不符合题意;
故选:C.
4.(3分)若a+b=3,ab=﹣12,则a2﹣ab+b2的值为( )
A.57 B.21 C.45 D.33
【思路点拔】先对原式进行变形,再计算即可.
【解答】解:a2﹣ab+b2
=a2+2ab+b2﹣3ab
=(a+b)2﹣3ab,
∵a+b=3,ab=﹣12,
∴原式=32﹣3×(﹣12)
=9+36
=45.
故选:C.
5.(3分)在运用乘法公式计算(2x﹣y+3)(2x+y﹣3)时,下列变形正确的是( )
A.[(2x﹣y)+3][(2x+y)﹣3] B.[(2x﹣y)+3][(2x﹣y)﹣3]
C.[2x﹣(y+3)][2x+(y﹣3)] D.[2x﹣(y﹣3)][2x+(y﹣3)]
【思路点拔】根据平方差结构特征进行解答即可.
【解答】解:(2x﹣y+3)(2x+y﹣3)=[2x﹣(y﹣3)][2x+(y﹣3)],
故选:D.
6.(3分)下列整式中不含有x+1这个因式的是( )
A.x2﹣1 B.x4﹣x3+x2﹣1
C.x3+1 D.x4﹣x3﹣x2﹣1
【思路点拔】将每个选项进行因式分解,即可作出判断.
【解答】解:A、x2﹣1=(x+1)(x﹣1),含有因式x+1,故此选项不符合题意;
B、x4﹣x3+x2﹣1=(x4﹣x3)+(x2﹣1)=x3(x﹣1)+(x+1)(x﹣1)=(x﹣1)(x3+x+1),不含有因式x+1,故此选项符合题意;
C、x3+1=(x+1)(x2﹣x+1),含有因式x+1,故此选项不符合题意;
D、x4﹣x3﹣x2﹣1=(x4﹣x2)﹣(x3+1)=x2(x2﹣1)﹣(x3+1)=x2(x+1)(x﹣1)﹣(x+1)(x2﹣x+1)=(x+1)(x3﹣x2﹣x2+x﹣1)=(x+1)(x3﹣2x2+x﹣1),含有因式x+1,故此选项不符合题意;
故选:B.
二.填空题(共6小题,满分18分,每小题3分)
7.(3分)当x满足x ≠3 时,(x﹣3)0有意义.
【思路点拔】根据指数幂的底数不为零的条件进行解题即可.
【解答】解:由题可知,
当x﹣3≠0时,(x﹣3)0有意义.
即x≠3.
故答案为:≠3.
8.(3分)若xa=3,x2a﹣3b,则xb的值为 5 .
【思路点拔】根据同底数幂的除法法则、幂的乘方与积的乘方法则进行解题即可.
【解答】解:∵xa=3,
∴x2a﹣3b=x2a÷x3b=(xa)2÷(xb)3=32÷(xb)3,
∴(xb)3=125,
∴xb=5.
故答案为:5.
9.(3分)关于x的多项式(x+1)(3x﹣n)展开合并后一次项系数为﹣1,则n的值为 4 .
【思路点拔】先根据多项式乘多项式法则计算,再根据展开式后一次项系数为﹣1得出3﹣n=﹣1,即可求出n的值.
【解答】解:(x+1)(3x﹣n)
=3x2﹣nx+3x﹣n
=3x2+(3﹣n)x﹣n,
∵关于x的多项式(x+1)(3x﹣n)展开合并后一次项系数为﹣1,
∴3﹣n=﹣1,
∴n=4,
故答案为:4.
10.(3分)设a为正整数,且满足a2+2a+40是完全平方数,则a的值是 18或4 .
【思路点拔】设设a2+2a+40=k2,其中k为正整数,则(a+1)2+39=k2,进而得(a+1+k)(a+1﹣k)=﹣39=﹣1×39=﹣3×13,再根据a,k均为正整数得a+1+k和a+1﹣k均为正整数,且a2+2a+40>40,则k>6,继而可得a+1+k>7,则①或②,然后解此方程组即可求出a的值.
【解答】解:∵a2+2a+40是完全平方数,
∴设a2+2a+40=k2,其中k为正整数,
∴(a+1)2+39=k2,
∴(a+1)2﹣k2=﹣39,
即(a+1+k)(a+1﹣k)=﹣39,
∵a,k均为正整数,
∴a+1+k和a+1﹣k均为整数,且a2+2a+40>40,
∴k2>40,
∴k>6且为整数,
∴a+1+k>7,
∵(a+1+k)(a+1﹣k)=﹣39=﹣1×39=﹣3×13,
∴①或②,
由①解得:,由②解得:,
∴a的值是18或4.
11.(3分)如果(m、n都是常数),那么n的值是 .
【思路点拔】根据(x+m)2=x2+2mx+m2,,得出,即可得出,n=m2,求出结果即可.
【解答】解:∵(x+m)2=x2+2mx+m2,,
∴,n=m2,
∴,
∴,
故答案为:.
12.(3分)若一个四位正整数满足:a+c=b+d,我们就称该数是“交替数”,则最小的“交替数”是 1001 ;若一个“交替数”m满足千位数字与百位数字的平方差是15,且十位数字与个位数的和能被5整除.则满足条件的“交替数”m的最大值为 8778 .
【思路点拔】根据最小的正整数是1,最大的一位数是9解答;根据题意得到:a2﹣b2=15,c+d=5k(k是正整数),a+c=b+d,联立方程组,解答即可.
【解答】解:a取最小的正整数1,c取最小的整数0,
则a+c=b+d,b=0,d=1.
∴最小的“交替数”是1001;
根据题意知:a2﹣b2=15,c+d=5k(k是正整数),a+c=b+d.
∵a2﹣b2=(a+b)(a﹣b)=15=15×1=5×3,且0≤a≤9,0≤b≤9,
∴或,
解得或,
∵a+c=b+d.
∴c﹣d=b﹣a,
∴c﹣d=﹣1或c﹣d=﹣3,
∵c+d=5k(k是正整数),
∴c+d=5或10或15,
∴或或或或或,
解得或或(舍去)或(舍去)或或,
∴a=8,b=7,c=2,d=3,即8723;
或a=4,b=1,c=1,d=4,即4114;
或a=8,b=7,c=7,d=8,即8778;
或a=4,b=1,c=6,d=9,即4169.
故所有的“交替数”是8723或4114或8778或4169,
最大的“交替数”为8778,
故答案为:1001,8778.
三.解答题(共11小题,满分84分)
13.(6分)(1)2x2 (x﹣1)+x3;
(2)(x2﹣2)(x+3)﹣x(x2+2x﹣1).
【思路点拔】(1)根据单项式乘多项式的运算法则计算,然后合并同类项即可;
(2)根据多项式乘多项式以及单项式乘多项式的运算法则计算,然后合并同类项即可.
【解答】解:(1)2x2 (x﹣1)+x3;
=2x3﹣2x2+x3
=3x3﹣2x2;
(2)(x2﹣2)(x+3)﹣x(x2+2x﹣1)
=x3+3x2﹣2x﹣6﹣x3﹣2x2+x
=x2﹣x﹣6.
14.(6分)已知3a=4,3b=10,3c=16.
(1)求3a+b的值;
(2)求32a﹣c的值.
【思路点拔】(1)利用同底数幂乘法法则计算即可;
(2)利用同底数幂除法法则,幂的乘方与积的乘方法则计算即可.
【解答】解:(1)∵3a=4,3b=10,
∴3a+b
=3a 3b
=4×10
=40;
(2)∵3a=4,3c=16,
∴32a﹣c
=(3a)2÷3c
=42÷16
=1.
15.(6分)(1)已知a2﹣a﹣5=0,求(4﹣a)(3+a)的值.
(2)已知a2+a﹣5=0,求(a2﹣5)(a+1)的值.
【思路点拔】(1)根据已知得a﹣a2=﹣5,再将(4﹣a)(3+a)化简,再整体代入即可;
(2)根据已知得a2﹣5=﹣a,﹣a2﹣a=﹣5,然后整体代入即可.
【解答】解:(1)∵a2﹣a﹣5=0,
∴a﹣a2=﹣5,
∴(4﹣a)(3+a)
=12+4a﹣3a﹣a2
=12+(a+a2)
=12+(﹣5)
=7;
(2)∵a2+a﹣5=0,
∴a2﹣5=﹣a,﹣a2﹣a=﹣5,
∴(a2﹣5)(a+1)
=﹣a(a+1)
=﹣a2﹣a
=﹣5.
16.(6分)利用乘法公式计算:
(1)(2+1)(22+1)(24+1);
(2)1002﹣992+982﹣972+…+22﹣12.
【思路点拔】(1)把所求算式乘以(2﹣1),再连续用平方差公式可算出答案;
(2)逆用平方差公式,再求和即可.
【解答】解:(1)原式=(2﹣1)(2+1)(22+1)(24+1)
=(22﹣1)(22+1)(24+1)
=(24﹣1)(24+1)
=28﹣1
=256﹣1
=255;
(2)原式=(100+99)×(100﹣99)+(98+97)×(98﹣97)+...+(2+1)×(2﹣1)
=100+99+98+97+...+2+1
=5050.
17.(6分)用简便方法计算:
(1);
(2)222﹣2×44+4.
【思路点拔】(1)先把原式变形为,然后根据平方差公式计算即可;
(2)根据完全平方公式先把原式变形为(22﹣2)2,然后计算即可.
【解答】(1)解:
=202
;
(2)222﹣2×44+4=(22﹣2)2=202=400.
18.(8分)因式分解:
(1)x2﹣12xy+36y2;
(2)3a2﹣27;
(3)6x(y2﹣2)﹣2x(2y2+3);
(4)4(a﹣b)x2﹣8xy(a﹣b)+4y2(a﹣b).
【思路点拔】(1)利用完全平方公式分解因式即可;
(2)先提公因式,再利用平方差公式分解因式即可;
(3)先提公因式,再利用平方差公式分解因式即可;
(4)先提公因式,再利用完全平方公式分解因式即可.
【解答】解:(1)x2﹣12xy+36y2=(x﹣6y)2;
(2)3a2﹣27
=3(a2﹣9)
=3(a+3)(a﹣3);
(3)6x(y2﹣2)﹣2x(2y2+3)
=2x[3(y2﹣2)﹣(2y2+3)]
=2x(y2﹣9)
=2x(y+3)(y﹣3);
(4)4(a﹣b)x2﹣8xy(a﹣b)+4y2(a﹣b)
=4(a﹣b)(x2﹣2xy+y2)
=4(a﹣b)(x﹣y)2.
19.(8分)已知xy=15,且满足(x2y﹣xy2)﹣(x﹣y)=28.
(1)求x﹣y的值;
(2)求x2+y2,x+y的值.
【思路点拔】(1)先利用提公因式结合已知条件得出14(x﹣y)=28,即可得解;
(2)根据x2+y2=(x﹣y)2+2xy即可求解;根据(x+y)2=x2+2xy+y2及平方根的定义即可求解.
【解答】解:(1)(x2y﹣xy2)﹣(x﹣y)=28,
xy(x﹣y)﹣(x﹣y)=28,
(x﹣y)(xy﹣1)=28,
∵xy=15,
∴14(x﹣y)=28,
∴x﹣y=2;
(2)x2+y2=(x﹣y)2+2xy=22+2×15=34;
(x+y)2=x2+2xy+y2=34+2×15=64,
∴x+y=±8.
20.(8分)我们知道,利用图形的面积能解释与得出代数恒等式,请你解答下列问题:
(1)如图,根据3个正方形和6个长方形的面积之和等于大正方形ABCD的面积.可以得到代数恒等式:(a+b+c)2= a2+b2+c2+2ab+2ac+2bc ;
(2)若n、t满足:(n﹣2024)2+(2026﹣2n)2+(n+1)2=t2+2t﹣18,(n﹣2024)(2026﹣2n)+(n﹣2024)(n+1)+(2026﹣2n)(n+1)=1﹣t,求t的值.
【思路点拔】(1)利用面积相等求解即可;
(2)利用(1)的结论,得到方程t2﹣16=9,求出t的值,再由t2+2t﹣18≥0,求符合条件的t的值即可.
【解答】解:(1)∵图中3个正方形的边长分别为a、b、c,
∴面积分别为a2,b2,c2,
边长为a、b的长方形有两个,边长为a、c的长方形有两个,边长为b、c的长方形有两个,
∴面积分别为ab,ac,bc,
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
故答案为:a2+b2+c2+2ab+2ac+2bc;
(2)∵(n﹣2024)(2026﹣2n)+(n﹣2024)(n+1)+(2026﹣2n)(n+1)=1﹣t,
∴2(n﹣2024)(2026﹣2n)+2(n﹣2024)(n+1)+2(2026﹣2n)(n+1)=2﹣2t,
∵(n﹣2024)2+(2026﹣2n)2+(n+1)2=t2+2t﹣18,
∴(n﹣2024+2026﹣2n+n+1)2=(n﹣2024)2+(2026﹣2n)2+(n+1)2+2(n﹣2024)(2026﹣2n)+2(n﹣2024)(n+1)+2(2026﹣2n)(n+1)=t2+2t﹣18+2﹣2t=t2﹣16,
∵n﹣2024+2026﹣2n+n+1=3,
∴t2﹣16=9,
解得t=±5,
∵t2+2t﹣18≥0,
∴t=﹣5舍去,
∴t=5.
21.(9分)因为x2+2x﹣3=(x+3)(x﹣1),这说明多项式x2+2x﹣3有一个因式为x﹣1,我们把x=1代入多项式,发现x=1能使多项式x2+2x﹣3的值为0.
利用上述规律,回答下列问题:
(1)若x﹣3是多项式x2+kx+12的一个因式,求k的值.
(2)若x﹣3和x﹣4是多项式x3+mx2+12x+n的两个因式,试求m、n的值,并将该多项式因式分解.
(3)分解因式:2x3﹣x2﹣5x﹣2.
【思路点拔】(1)由已知条件可知,当x=3时,x2+kx+12=0,将x的值代入即可求得;
(2)由题意可知,x=3和x=4时,x3+mx2+12x+n=0,由此得二元一次方程组,从而可求得m和n的值;
(3)将x=﹣1代入原式得:﹣2﹣1+5﹣2=0则x+1是原式的因式,利用竖式除法可得另一个因式,据此分解即可.
【解答】解:(1)∵x﹣3是多项式x2+kx+12的一个因式,
∴x=3时,x2+kx+12=0,
∴9+3k+12=0,
∴3k=﹣21,
∴k=﹣7,
∴k的值为﹣7;
(2)(x﹣3)和(x﹣4)是多项式x3+mx2+12x+n的两个因式,
∴x=3和x=4时,x3+mx2+12x+n=0,
∴,
解得,
∴m、n的值分别为﹣7和0,
(3)将x=﹣1代入原式得:﹣2﹣1+5﹣2=0,
∴x+1是原式的因式,根据用竖式除法可得:2x3﹣x2﹣5x﹣2=(2x2﹣3x﹣2)(x+1)=(x﹣2)(2x+1)(x+1).
22.(9分)在《整式乘除》中学习了完全平方公式,还记得它是如何被发现的吗?把图①看作一个大正方形,它的面积是(a+b)2,如果把图①看作是由2个长方形和2个小正方形组成的,它的面积为a2+2ab+b2,由此得到;(a+b)2=a2+2ab+b2.
[类比探究]如图②,正方形ABCD的边长是c,它由四个直角边长分别是a,b的直角三角形和中间一个小正方形组成的,对图②的面积进行计算,你发现的式子是 c2=a2+b2 .(用a,b,c表示,结果化为最简)
[联系运用]如图②,正方形ABCD的边长是c,它由四个直角边长分别是a,b的直角三角形和一个小正方形组成的,当c=5,a﹣b时,求a+b的值.
[问题解决]如图③,将四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形ABCDEFGH.若该图形的周长为80,OA=12.求该图形的面积.
【思路点拔】[类比探究]利用正方形ABCD的面积=边长为(a﹣b)的正方形和四个全等的直角边分别为a,b的直角三角形的面积之和解答即可;
[联系运用]利用关系式求得2ab=23,再利用(a+b)2=a2+2ab+b2解答即可;
[问题解决]由已知可得:OA=OC=OE=OG=12,AH=BC=DE=FG,AB=CD=EF=GH,设OH=x,则AH=BC=DE=FG=12﹣x,利用周长为80列出关于x的方程,解方程求得x的值,再利用三角形的面积公式解答即可.
【解答】解:[类比探究]∵正方形ABCD的边长是c,
∴正方形ABCD的面积为c2,
∵正方形ABCD的面积由边长为(a﹣b)的正方形和四个全等的直角边分别为a,b的直角三角形拼成,
∴正方形ABCD的面积为(a﹣b)2+4ab=(a﹣b)2+2ab=a2+b2,
∴c2=a2+b2.
故答案为:c2=a2+b2;
[联系运用]由[类比探究]可得:a2+b2=c2=25,
∵a﹣b,
∴(a﹣b)2=2,
∴a2﹣2ab+b2=2,
∴2ab=23.
∵(a+b)2=a2+2ab+b2,
∴(a+b)2=25+23=48.
∵a+b>0,
∴a+b.
[问题解决]∵将四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形ABCDEFGH,
∴OA=OC=OE=OG=12,AH=BC=DE=FG,AB=CD=EF=GH,
设OH=x,则AH=BC=DE=FG=12﹣x,
∴AB.
∵图形的周长为80,
∴44(12﹣x)=80,
解得:x=5.
经检验:x=5是原方程的解.
∴OH=OB=OD=OF=5,
∴该图形的面积=45×12=120.
23.(12分)阅读材料,解决问题
【材料1】将形如x2+px+q的二次三项式因式分解时,如果能满足q=mn且p=m+n,则可以把x2+px+q因式分解成(x+m)(x+n).
如,x2+4x+3中,常数项3=1×3,一次项系数4=1+3,∴x2+4x+3=(x+1)(x+3);同理,x2﹣4x﹣12中,常数项“﹣12”=﹣6×2,一次项系数“﹣4”=﹣6+2,
∴x2﹣4x﹣12=(x﹣6)(x+2).
【材料2】因式分解:(x+y)2+2(x+y)+1
解:把x+y看成一个整体,令x+y=A,则
原式=A2+2A+1=(A+1)2,再将A=x+y重新代入,得:原式=(x+y+1)2.
上述解题用到的“整体思想”是数学解题中常见的思想方法.请你解答下列问题:
(1)根据材料1,因式分解x2﹣6x+8;
(2)结合材料1和材料2,完成下面小题:
①分解因式:(x﹣y)2+4(x﹣y)+3;
②分解因式:m(m+2)(m2+2m﹣2)﹣3.
【思路点拔】(1)利用材料1的解题思路进行计算,即可解答;
(2)①利用材料1和材料2的解题思路进行计算,即可解答;
②利用材料1和材料2的解题思路进行计算,即可解答.
【解答】解:(1)x2﹣6x+8=(x﹣2)(x﹣4);
(2)①把x﹣y看成一个整体,令x﹣y=A,则
原式=A2+4A+3=(A+1)(A+3),
再将A=x﹣y重新代入,得:原式=(x﹣y+1)(x﹣y+3);
②m(m+2)(m2+2m﹣2)﹣3
=(m2+2m)(m2+2m﹣2)﹣3
=(m2+2m)2﹣2(m2+2m)﹣3,
把m2+2m看成一个整体,令m2+2m=A,则
原式=A2﹣2A﹣3=(A﹣3)(A+1),
再将A=m2+2m重新代入,得:原式=(m2+2m﹣3)(m2+2m+1)=(m+3)(m﹣1)(m+1)2.
整式的乘法与因式分解 单元训练(一)
一.选择题(共6小题,满分18分,每小题3分)
1.(3分)下列运算正确的是( )
A.x6+x6=2x12
B.(﹣2a2b)3=﹣8a8b3
C.[﹣(m﹣n)3]2=[﹣(m﹣n)2]3
D.(﹣y4) (﹣y)6÷(﹣y)7=y3
2.(3分)若6x=3,6y=16,则6x﹣y的值为( )
A. B.﹣13 C. D.19
3.(3分)下列各式能用平方差公式计算的是( )
A.(a﹣b)(b﹣a) B.(a+b)(b+a)
C.(a﹣b)(﹣a﹣b) D.(a+b)(﹣a﹣b)
4.(3分)若a+b=3,ab=﹣12,则a2﹣ab+b2的值为( )
A.57 B.21 C.45 D.33
5.(3分)在运用乘法公式计算(2x﹣y+3)(2x+y﹣3)时,下列变形正确的是( )
A.[(2x﹣y)+3][(2x+y)﹣3] B.[(2x﹣y)+3][(2x﹣y)﹣3]
C.[2x﹣(y+3)][2x+(y﹣3)] D.[2x﹣(y﹣3)][2x+(y﹣3)]
6.(3分)下列整式中不含有x+1这个因式的是( )
A.x2﹣1 B.x4﹣x3+x2﹣1
C.x3+1 D.x4﹣x3﹣x2﹣1
二.填空题(共6小题,满分18分,每小题3分)
7.(3分)当x满足x 时,(x﹣3)0有意义.
8.(3分)若xa=3,x2a﹣3b,则xb的值为 .
9.(3分)关于x的多项式(x+1)(3x﹣n)展开合并后一次项系数为﹣1,则n的值为 .
10.(3分)设a为正整数,且满足a2+2a+40是完全平方数,则a的值是 .
11.(3分)如果(m、n都是常数),那么n的值是 .
12.(3分)若一个四位正整数满足:a+c=b+d,我们就称该数是“交替数”,则最小的“交替数”是 ;若一个“交替数”m满足千位数字与百位数字的平方差是15,且十位数字与个位数的和能被5整除.则满足条件的“交替数”m的最大值为 .
三.解答题(共11小题,满分84分)
13.(6分)(1)2x2 (x﹣1)+x3;
(2)(x2﹣2)(x+3)﹣x(x2+2x﹣1).
14.(6分)已知3a=4,3b=10,3c=16.
(1)求3a+b的值;
(2)求32a﹣c的值.
15.(6分)(1)已知a2﹣a﹣5=0,求(4﹣a)(3+a)的值.
(2)已知a2+a﹣5=0,求(a2﹣5)(a+1)的值.
16.(6分)利用乘法公式计算:
(1)(2+1)(22+1)(24+1);
(2)1002﹣992+982﹣972+…+22﹣12.
17.(6分)用简便方法计算:
(1);
(2)222﹣2×44+4.
18.(8分)因式分解:
(1)x2﹣12xy+36y2;
(2)3a2﹣27;
(3)6x(y2﹣2)﹣2x(2y2+3);
(4)4(a﹣b)x2﹣8xy(a﹣b)+4y2(a﹣b).
19.(8分)已知xy=15,且满足(x2y﹣xy2)﹣(x﹣y)=28.
(1)求x﹣y的值;
(2)求x2+y2,x+y的值.
20.(8分)我们知道,利用图形的面积能解释与得出代数恒等式,请你解答下列问题:
(1)如图,根据3个正方形和6个长方形的面积之和等于大正方形ABCD的面积.可以得到代数恒等式:(a+b+c)2= ;
(2)若n、t满足:(n﹣2024)2+(2026﹣2n)2+(n+1)2=t2+2t﹣18,(n﹣2024)(2026﹣2n)+(n﹣2024)(n+1)+(2026﹣2n)(n+1)=1﹣t,求t的值.
21.(9分)因为x2+2x﹣3=(x+3)(x﹣1),这说明多项式x2+2x﹣3有一个因式为x﹣1,我们把x=1代入多项式,发现x=1能使多项式x2+2x﹣3的值为0.
利用上述规律,回答下列问题:
(1)若x﹣3是多项式x2+kx+12的一个因式,求k的值.
(2)若x﹣3和x﹣4是多项式x3+mx2+12x+n的两个因式,试求m、n的值,并将该多项式因式分解.
(3)分解因式:2x3﹣x2﹣5x﹣2.
22.(9分)在《整式乘除》中学习了完全平方公式,还记得它是如何被发现的吗?把图①看作一个大正方形,它的面积是(a+b)2,如果把图①看作是由2个长方形和2个小正方形组成的,它的面积为a2+2ab+b2,由此得到;(a+b)2=a2+2ab+b2.
[类比探究]如图②,正方形ABCD的边长是c,它由四个直角边长分别是a,b的直角三角形和中间一个小正方形组成的,对图②的面积进行计算,你发现的式子是 .(用a,b,c表示,结果化为最简)
[联系运用]如图②,正方形ABCD的边长是c,它由四个直角边长分别是a,b的直角三角形和一个小正方形组成的,当c=5,a﹣b时,求a+b的值.
[问题解决]如图③,将四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形ABCDEFGH.若该图形的周长为80,OA=12.求该图形的面积.
23.(12分)阅读材料,解决问题
【材料1】将形如x2+px+q的二次三项式因式分解时,如果能满足q=mn且p=m+n,则可以把x2+px+q因式分解成(x+m)(x+n).
如,x2+4x+3中,常数项3=1×3,一次项系数4=1+3,∴x2+4x+3=(x+1)(x+3);同理,x2﹣4x﹣12中,常数项“﹣12”=﹣6×2,一次项系数“﹣4”=﹣6+2,
∴x2﹣4x﹣12=(x﹣6)(x+2).
【材料2】因式分解:(x+y)2+2(x+y)+1
解:把x+y看成一个整体,令x+y=A,则
原式=A2+2A+1=(A+1)2,再将A=x+y重新代入,得:原式=(x+y+1)2.
上述解题用到的“整体思想”是数学解题中常见的思想方法.请你解答下列问题:
(1)根据材料1,因式分解x2﹣6x+8;
(2)结合材料1和材料2,完成下面小题:
①分解因式:(x﹣y)2+4(x﹣y)+3;
②分解因式:m(m+2)(m2+2m﹣2)﹣3.
整式的乘法与因式分解 单元训练(一)
一.选择题(共6小题,满分18分,每小题3分)
1.(3分)下列运算正确的是( )
A.x6+x6=2x12
B.(﹣2a2b)3=﹣8a8b3
C.[﹣(m﹣n)3]2=[﹣(m﹣n)2]3
D.(﹣y4) (﹣y)6÷(﹣y)7=y3
【思路点拔】根据同底数幂的乘除法法则、幂的乘方与积的乘方法则、合并同类项的方法进行解题即可.
【解答】解:A、x6+x6=2x6,故该项不正确,不符合题意;
B、(﹣2a2b)3=﹣8a6b3,故该项不正确,不符合题意;
C、[﹣(m﹣n)3]2=(m﹣n)6,[﹣(m﹣n)2]3=﹣(m﹣n)6,两者不相等,故该项不正确,不符合题意;
D、(﹣y4) (﹣y)6÷(﹣y)7=﹣y10÷(﹣y)7=y3,故该项正确,符合题意;
故选:D.
2.(3分)若6x=3,6y=16,则6x﹣y的值为( )
A. B.﹣13 C. D.19
【思路点拔】根据同底数幂的除法法则进行计算,即可解答.
【解答】解:∵6x=3,6y=16,
∴6x﹣y=6x÷6y=3÷16,
故选:A.
3.(3分)下列各式能用平方差公式计算的是( )
A.(a﹣b)(b﹣a) B.(a+b)(b+a)
C.(a﹣b)(﹣a﹣b) D.(a+b)(﹣a﹣b)
【思路点拔】根据平方差公式、完全平方公式的结构特征逐项判断即可.
【解答】解:A、(a﹣b)(b﹣a)=﹣(a﹣b)(a﹣b)=﹣(a﹣b)2=﹣(a2﹣2ab+b2)=﹣a2+2ab﹣b2,不能用平方差公式计算,故此选项不符合题意;
B、(a+b)(b+a)=(a+b)(a+b)=(a+b)2=a2+2ab+b2,不能用平方差公式计算,故此选项不符合题意;
C、(a﹣b)(﹣a﹣b)=﹣(a﹣b)(a+b)=﹣(a2﹣b2)=﹣a2+b2,能用平方差公式计算,故此选项符合题意;
D、(a+b)(﹣a﹣b)=﹣(a+b)(a+b)﹣(a+b)2=﹣(a2+2ab+b2)=﹣a2﹣2ab﹣b2,不能用平方差公式计算,故此选项不符合题意;
故选:C.
4.(3分)若a+b=3,ab=﹣12,则a2﹣ab+b2的值为( )
A.57 B.21 C.45 D.33
【思路点拔】先对原式进行变形,再计算即可.
【解答】解:a2﹣ab+b2
=a2+2ab+b2﹣3ab
=(a+b)2﹣3ab,
∵a+b=3,ab=﹣12,
∴原式=32﹣3×(﹣12)
=9+36
=45.
故选:C.
5.(3分)在运用乘法公式计算(2x﹣y+3)(2x+y﹣3)时,下列变形正确的是( )
A.[(2x﹣y)+3][(2x+y)﹣3] B.[(2x﹣y)+3][(2x﹣y)﹣3]
C.[2x﹣(y+3)][2x+(y﹣3)] D.[2x﹣(y﹣3)][2x+(y﹣3)]
【思路点拔】根据平方差结构特征进行解答即可.
【解答】解:(2x﹣y+3)(2x+y﹣3)=[2x﹣(y﹣3)][2x+(y﹣3)],
故选:D.
6.(3分)下列整式中不含有x+1这个因式的是( )
A.x2﹣1 B.x4﹣x3+x2﹣1
C.x3+1 D.x4﹣x3﹣x2﹣1
【思路点拔】将每个选项进行因式分解,即可作出判断.
【解答】解:A、x2﹣1=(x+1)(x﹣1),含有因式x+1,故此选项不符合题意;
B、x4﹣x3+x2﹣1=(x4﹣x3)+(x2﹣1)=x3(x﹣1)+(x+1)(x﹣1)=(x﹣1)(x3+x+1),不含有因式x+1,故此选项符合题意;
C、x3+1=(x+1)(x2﹣x+1),含有因式x+1,故此选项不符合题意;
D、x4﹣x3﹣x2﹣1=(x4﹣x2)﹣(x3+1)=x2(x2﹣1)﹣(x3+1)=x2(x+1)(x﹣1)﹣(x+1)(x2﹣x+1)=(x+1)(x3﹣x2﹣x2+x﹣1)=(x+1)(x3﹣2x2+x﹣1),含有因式x+1,故此选项不符合题意;
故选:B.
二.填空题(共6小题,满分18分,每小题3分)
7.(3分)当x满足x ≠3 时,(x﹣3)0有意义.
【思路点拔】根据指数幂的底数不为零的条件进行解题即可.
【解答】解:由题可知,
当x﹣3≠0时,(x﹣3)0有意义.
即x≠3.
故答案为:≠3.
8.(3分)若xa=3,x2a﹣3b,则xb的值为 5 .
【思路点拔】根据同底数幂的除法法则、幂的乘方与积的乘方法则进行解题即可.
【解答】解:∵xa=3,
∴x2a﹣3b=x2a÷x3b=(xa)2÷(xb)3=32÷(xb)3,
∴(xb)3=125,
∴xb=5.
故答案为:5.
9.(3分)关于x的多项式(x+1)(3x﹣n)展开合并后一次项系数为﹣1,则n的值为 4 .
【思路点拔】先根据多项式乘多项式法则计算,再根据展开式后一次项系数为﹣1得出3﹣n=﹣1,即可求出n的值.
【解答】解:(x+1)(3x﹣n)
=3x2﹣nx+3x﹣n
=3x2+(3﹣n)x﹣n,
∵关于x的多项式(x+1)(3x﹣n)展开合并后一次项系数为﹣1,
∴3﹣n=﹣1,
∴n=4,
故答案为:4.
10.(3分)设a为正整数,且满足a2+2a+40是完全平方数,则a的值是 18或4 .
【思路点拔】设设a2+2a+40=k2,其中k为正整数,则(a+1)2+39=k2,进而得(a+1+k)(a+1﹣k)=﹣39=﹣1×39=﹣3×13,再根据a,k均为正整数得a+1+k和a+1﹣k均为正整数,且a2+2a+40>40,则k>6,继而可得a+1+k>7,则①或②,然后解此方程组即可求出a的值.
【解答】解:∵a2+2a+40是完全平方数,
∴设a2+2a+40=k2,其中k为正整数,
∴(a+1)2+39=k2,
∴(a+1)2﹣k2=﹣39,
即(a+1+k)(a+1﹣k)=﹣39,
∵a,k均为正整数,
∴a+1+k和a+1﹣k均为整数,且a2+2a+40>40,
∴k2>40,
∴k>6且为整数,
∴a+1+k>7,
∵(a+1+k)(a+1﹣k)=﹣39=﹣1×39=﹣3×13,
∴①或②,
由①解得:,由②解得:,
∴a的值是18或4.
11.(3分)如果(m、n都是常数),那么n的值是 .
【思路点拔】根据(x+m)2=x2+2mx+m2,,得出,即可得出,n=m2,求出结果即可.
【解答】解:∵(x+m)2=x2+2mx+m2,,
∴,n=m2,
∴,
∴,
故答案为:.
12.(3分)若一个四位正整数满足:a+c=b+d,我们就称该数是“交替数”,则最小的“交替数”是 1001 ;若一个“交替数”m满足千位数字与百位数字的平方差是15,且十位数字与个位数的和能被5整除.则满足条件的“交替数”m的最大值为 8778 .
【思路点拔】根据最小的正整数是1,最大的一位数是9解答;根据题意得到:a2﹣b2=15,c+d=5k(k是正整数),a+c=b+d,联立方程组,解答即可.
【解答】解:a取最小的正整数1,c取最小的整数0,
则a+c=b+d,b=0,d=1.
∴最小的“交替数”是1001;
根据题意知:a2﹣b2=15,c+d=5k(k是正整数),a+c=b+d.
∵a2﹣b2=(a+b)(a﹣b)=15=15×1=5×3,且0≤a≤9,0≤b≤9,
∴或,
解得或,
∵a+c=b+d.
∴c﹣d=b﹣a,
∴c﹣d=﹣1或c﹣d=﹣3,
∵c+d=5k(k是正整数),
∴c+d=5或10或15,
∴或或或或或,
解得或或(舍去)或(舍去)或或,
∴a=8,b=7,c=2,d=3,即8723;
或a=4,b=1,c=1,d=4,即4114;
或a=8,b=7,c=7,d=8,即8778;
或a=4,b=1,c=6,d=9,即4169.
故所有的“交替数”是8723或4114或8778或4169,
最大的“交替数”为8778,
故答案为:1001,8778.
三.解答题(共11小题,满分84分)
13.(6分)(1)2x2 (x﹣1)+x3;
(2)(x2﹣2)(x+3)﹣x(x2+2x﹣1).
【思路点拔】(1)根据单项式乘多项式的运算法则计算,然后合并同类项即可;
(2)根据多项式乘多项式以及单项式乘多项式的运算法则计算,然后合并同类项即可.
【解答】解:(1)2x2 (x﹣1)+x3;
=2x3﹣2x2+x3
=3x3﹣2x2;
(2)(x2﹣2)(x+3)﹣x(x2+2x﹣1)
=x3+3x2﹣2x﹣6﹣x3﹣2x2+x
=x2﹣x﹣6.
14.(6分)已知3a=4,3b=10,3c=16.
(1)求3a+b的值;
(2)求32a﹣c的值.
【思路点拔】(1)利用同底数幂乘法法则计算即可;
(2)利用同底数幂除法法则,幂的乘方与积的乘方法则计算即可.
【解答】解:(1)∵3a=4,3b=10,
∴3a+b
=3a 3b
=4×10
=40;
(2)∵3a=4,3c=16,
∴32a﹣c
=(3a)2÷3c
=42÷16
=1.
15.(6分)(1)已知a2﹣a﹣5=0,求(4﹣a)(3+a)的值.
(2)已知a2+a﹣5=0,求(a2﹣5)(a+1)的值.
【思路点拔】(1)根据已知得a﹣a2=﹣5,再将(4﹣a)(3+a)化简,再整体代入即可;
(2)根据已知得a2﹣5=﹣a,﹣a2﹣a=﹣5,然后整体代入即可.
【解答】解:(1)∵a2﹣a﹣5=0,
∴a﹣a2=﹣5,
∴(4﹣a)(3+a)
=12+4a﹣3a﹣a2
=12+(a+a2)
=12+(﹣5)
=7;
(2)∵a2+a﹣5=0,
∴a2﹣5=﹣a,﹣a2﹣a=﹣5,
∴(a2﹣5)(a+1)
=﹣a(a+1)
=﹣a2﹣a
=﹣5.
16.(6分)利用乘法公式计算:
(1)(2+1)(22+1)(24+1);
(2)1002﹣992+982﹣972+…+22﹣12.
【思路点拔】(1)把所求算式乘以(2﹣1),再连续用平方差公式可算出答案;
(2)逆用平方差公式,再求和即可.
【解答】解:(1)原式=(2﹣1)(2+1)(22+1)(24+1)
=(22﹣1)(22+1)(24+1)
=(24﹣1)(24+1)
=28﹣1
=256﹣1
=255;
(2)原式=(100+99)×(100﹣99)+(98+97)×(98﹣97)+...+(2+1)×(2﹣1)
=100+99+98+97+...+2+1
=5050.
17.(6分)用简便方法计算:
(1);
(2)222﹣2×44+4.
【思路点拔】(1)先把原式变形为,然后根据平方差公式计算即可;
(2)根据完全平方公式先把原式变形为(22﹣2)2,然后计算即可.
【解答】(1)解:
=202
;
(2)222﹣2×44+4=(22﹣2)2=202=400.
18.(8分)因式分解:
(1)x2﹣12xy+36y2;
(2)3a2﹣27;
(3)6x(y2﹣2)﹣2x(2y2+3);
(4)4(a﹣b)x2﹣8xy(a﹣b)+4y2(a﹣b).
【思路点拔】(1)利用完全平方公式分解因式即可;
(2)先提公因式,再利用平方差公式分解因式即可;
(3)先提公因式,再利用平方差公式分解因式即可;
(4)先提公因式,再利用完全平方公式分解因式即可.
【解答】解:(1)x2﹣12xy+36y2=(x﹣6y)2;
(2)3a2﹣27
=3(a2﹣9)
=3(a+3)(a﹣3);
(3)6x(y2﹣2)﹣2x(2y2+3)
=2x[3(y2﹣2)﹣(2y2+3)]
=2x(y2﹣9)
=2x(y+3)(y﹣3);
(4)4(a﹣b)x2﹣8xy(a﹣b)+4y2(a﹣b)
=4(a﹣b)(x2﹣2xy+y2)
=4(a﹣b)(x﹣y)2.
19.(8分)已知xy=15,且满足(x2y﹣xy2)﹣(x﹣y)=28.
(1)求x﹣y的值;
(2)求x2+y2,x+y的值.
【思路点拔】(1)先利用提公因式结合已知条件得出14(x﹣y)=28,即可得解;
(2)根据x2+y2=(x﹣y)2+2xy即可求解;根据(x+y)2=x2+2xy+y2及平方根的定义即可求解.
【解答】解:(1)(x2y﹣xy2)﹣(x﹣y)=28,
xy(x﹣y)﹣(x﹣y)=28,
(x﹣y)(xy﹣1)=28,
∵xy=15,
∴14(x﹣y)=28,
∴x﹣y=2;
(2)x2+y2=(x﹣y)2+2xy=22+2×15=34;
(x+y)2=x2+2xy+y2=34+2×15=64,
∴x+y=±8.
20.(8分)我们知道,利用图形的面积能解释与得出代数恒等式,请你解答下列问题:
(1)如图,根据3个正方形和6个长方形的面积之和等于大正方形ABCD的面积.可以得到代数恒等式:(a+b+c)2= a2+b2+c2+2ab+2ac+2bc ;
(2)若n、t满足:(n﹣2024)2+(2026﹣2n)2+(n+1)2=t2+2t﹣18,(n﹣2024)(2026﹣2n)+(n﹣2024)(n+1)+(2026﹣2n)(n+1)=1﹣t,求t的值.
【思路点拔】(1)利用面积相等求解即可;
(2)利用(1)的结论,得到方程t2﹣16=9,求出t的值,再由t2+2t﹣18≥0,求符合条件的t的值即可.
【解答】解:(1)∵图中3个正方形的边长分别为a、b、c,
∴面积分别为a2,b2,c2,
边长为a、b的长方形有两个,边长为a、c的长方形有两个,边长为b、c的长方形有两个,
∴面积分别为ab,ac,bc,
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
故答案为:a2+b2+c2+2ab+2ac+2bc;
(2)∵(n﹣2024)(2026﹣2n)+(n﹣2024)(n+1)+(2026﹣2n)(n+1)=1﹣t,
∴2(n﹣2024)(2026﹣2n)+2(n﹣2024)(n+1)+2(2026﹣2n)(n+1)=2﹣2t,
∵(n﹣2024)2+(2026﹣2n)2+(n+1)2=t2+2t﹣18,
∴(n﹣2024+2026﹣2n+n+1)2=(n﹣2024)2+(2026﹣2n)2+(n+1)2+2(n﹣2024)(2026﹣2n)+2(n﹣2024)(n+1)+2(2026﹣2n)(n+1)=t2+2t﹣18+2﹣2t=t2﹣16,
∵n﹣2024+2026﹣2n+n+1=3,
∴t2﹣16=9,
解得t=±5,
∵t2+2t﹣18≥0,
∴t=﹣5舍去,
∴t=5.
21.(9分)因为x2+2x﹣3=(x+3)(x﹣1),这说明多项式x2+2x﹣3有一个因式为x﹣1,我们把x=1代入多项式,发现x=1能使多项式x2+2x﹣3的值为0.
利用上述规律,回答下列问题:
(1)若x﹣3是多项式x2+kx+12的一个因式,求k的值.
(2)若x﹣3和x﹣4是多项式x3+mx2+12x+n的两个因式,试求m、n的值,并将该多项式因式分解.
(3)分解因式:2x3﹣x2﹣5x﹣2.
【思路点拔】(1)由已知条件可知,当x=3时,x2+kx+12=0,将x的值代入即可求得;
(2)由题意可知,x=3和x=4时,x3+mx2+12x+n=0,由此得二元一次方程组,从而可求得m和n的值;
(3)将x=﹣1代入原式得:﹣2﹣1+5﹣2=0则x+1是原式的因式,利用竖式除法可得另一个因式,据此分解即可.
【解答】解:(1)∵x﹣3是多项式x2+kx+12的一个因式,
∴x=3时,x2+kx+12=0,
∴9+3k+12=0,
∴3k=﹣21,
∴k=﹣7,
∴k的值为﹣7;
(2)(x﹣3)和(x﹣4)是多项式x3+mx2+12x+n的两个因式,
∴x=3和x=4时,x3+mx2+12x+n=0,
∴,
解得,
∴m、n的值分别为﹣7和0,
(3)将x=﹣1代入原式得:﹣2﹣1+5﹣2=0,
∴x+1是原式的因式,根据用竖式除法可得:2x3﹣x2﹣5x﹣2=(2x2﹣3x﹣2)(x+1)=(x﹣2)(2x+1)(x+1).
22.(9分)在《整式乘除》中学习了完全平方公式,还记得它是如何被发现的吗?把图①看作一个大正方形,它的面积是(a+b)2,如果把图①看作是由2个长方形和2个小正方形组成的,它的面积为a2+2ab+b2,由此得到;(a+b)2=a2+2ab+b2.
[类比探究]如图②,正方形ABCD的边长是c,它由四个直角边长分别是a,b的直角三角形和中间一个小正方形组成的,对图②的面积进行计算,你发现的式子是 c2=a2+b2 .(用a,b,c表示,结果化为最简)
[联系运用]如图②,正方形ABCD的边长是c,它由四个直角边长分别是a,b的直角三角形和一个小正方形组成的,当c=5,a﹣b时,求a+b的值.
[问题解决]如图③,将四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形ABCDEFGH.若该图形的周长为80,OA=12.求该图形的面积.
【思路点拔】[类比探究]利用正方形ABCD的面积=边长为(a﹣b)的正方形和四个全等的直角边分别为a,b的直角三角形的面积之和解答即可;
[联系运用]利用关系式求得2ab=23,再利用(a+b)2=a2+2ab+b2解答即可;
[问题解决]由已知可得:OA=OC=OE=OG=12,AH=BC=DE=FG,AB=CD=EF=GH,设OH=x,则AH=BC=DE=FG=12﹣x,利用周长为80列出关于x的方程,解方程求得x的值,再利用三角形的面积公式解答即可.
【解答】解:[类比探究]∵正方形ABCD的边长是c,
∴正方形ABCD的面积为c2,
∵正方形ABCD的面积由边长为(a﹣b)的正方形和四个全等的直角边分别为a,b的直角三角形拼成,
∴正方形ABCD的面积为(a﹣b)2+4ab=(a﹣b)2+2ab=a2+b2,
∴c2=a2+b2.
故答案为:c2=a2+b2;
[联系运用]由[类比探究]可得:a2+b2=c2=25,
∵a﹣b,
∴(a﹣b)2=2,
∴a2﹣2ab+b2=2,
∴2ab=23.
∵(a+b)2=a2+2ab+b2,
∴(a+b)2=25+23=48.
∵a+b>0,
∴a+b.
[问题解决]∵将四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形ABCDEFGH,
∴OA=OC=OE=OG=12,AH=BC=DE=FG,AB=CD=EF=GH,
设OH=x,则AH=BC=DE=FG=12﹣x,
∴AB.
∵图形的周长为80,
∴44(12﹣x)=80,
解得:x=5.
经检验:x=5是原方程的解.
∴OH=OB=OD=OF=5,
∴该图形的面积=45×12=120.
23.(12分)阅读材料,解决问题
【材料1】将形如x2+px+q的二次三项式因式分解时,如果能满足q=mn且p=m+n,则可以把x2+px+q因式分解成(x+m)(x+n).
如,x2+4x+3中,常数项3=1×3,一次项系数4=1+3,∴x2+4x+3=(x+1)(x+3);同理,x2﹣4x﹣12中,常数项“﹣12”=﹣6×2,一次项系数“﹣4”=﹣6+2,
∴x2﹣4x﹣12=(x﹣6)(x+2).
【材料2】因式分解:(x+y)2+2(x+y)+1
解:把x+y看成一个整体,令x+y=A,则
原式=A2+2A+1=(A+1)2,再将A=x+y重新代入,得:原式=(x+y+1)2.
上述解题用到的“整体思想”是数学解题中常见的思想方法.请你解答下列问题:
(1)根据材料1,因式分解x2﹣6x+8;
(2)结合材料1和材料2,完成下面小题:
①分解因式:(x﹣y)2+4(x﹣y)+3;
②分解因式:m(m+2)(m2+2m﹣2)﹣3.
【思路点拔】(1)利用材料1的解题思路进行计算,即可解答;
(2)①利用材料1和材料2的解题思路进行计算,即可解答;
②利用材料1和材料2的解题思路进行计算,即可解答.
【解答】解:(1)x2﹣6x+8=(x﹣2)(x﹣4);
(2)①把x﹣y看成一个整体,令x﹣y=A,则
原式=A2+4A+3=(A+1)(A+3),
再将A=x﹣y重新代入,得:原式=(x﹣y+1)(x﹣y+3);
②m(m+2)(m2+2m﹣2)﹣3
=(m2+2m)(m2+2m﹣2)﹣3
=(m2+2m)2﹣2(m2+2m)﹣3,
把m2+2m看成一个整体,令m2+2m=A,则
原式=A2﹣2A﹣3=(A﹣3)(A+1),
再将A=m2+2m重新代入,得:原式=(m2+2m﹣3)(m2+2m+1)=(m+3)(m﹣1)(m+1)2.
