整式的乘法与因式分解 单元训练(二)(含解析)
文档属性
| 名称 | 整式的乘法与因式分解 单元训练(二)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 319.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-18 21:45:06 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
整式的乘法与因式分解 单元训练(二)
一.选择题(共6小题,满分18分,每小题3分)
1.(3分)下列运算正确的是( )
A.x2+x3=x5 B.(x2)3=x6
C.x4 x3=x12 D.4x2 y2=(4xy)2
2.(3分)计算:(14a3b2﹣7ab2)÷7ab2的结果是( )
A.2a2 B.2a2﹣1 C.2a2﹣b D.2a2b﹣1
3.(3分)若(x﹣1)(x+2)=ax2+bx+c,则代数式a+b+c的值为( )
A.2 B.0 C.﹣2 D.﹣4
4.(3分)若a﹣b=8,a2+b2=82,则2ab的值为( )
A.9 B.﹣9 C.18 D.﹣18
5.(3分)如图①,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形(如图②),通过计算两个图形的面积,验证了一个等式,则这个等式是( )
A.(a+2b)(a﹣b)=a2+ab﹣2b2
B.a2﹣b2=(a+b)(a﹣b)
C.(a﹣b)2=a2﹣2ab+b2
D.(a+b)2=a2+2ab+b2
6.(3分)下列等式中,哪些从左到右的变形是因式分解( )
A.(x+y)(x﹣2y)=x2﹣xy﹣2y2
B.
C.3x2﹣5x﹣2=(3x+1)(x﹣2)
D.3x2+6x+4=3(x+1)2+1
二.填空题(共6小题,满分18分,每小题3分)
7.(3分)比较大小:2m+n+1 4m+4n.
8.(3分)已知4x=2y﹣1,3y+1=27x﹣2,则x﹣y= .
9.(3分)计算: .
10.(3分)在横线上填入适当的整式:
(1)(﹣3x2+2y2)( )=9x4﹣4y4;
(2)a2+3ab+b2+ =(a﹣b)2.
11.(3分)如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个长方形(不重叠无缝隙),则长方形的面积为 cm2.
12.(3分)若对于一个四位正整数,其千位数字的2倍和百位数字之和为14,十位数字的2倍和个位数字的3倍之和为15,则称这样的四位数为“凸月数”.把任意四位数A的前两位上的数字和后两位上的数字整体交换,得到新四位数A′,规定F(A).则F(6233)的值为 .若s=2640+1000a+100b+10c+d(0≤a≤6,3<b≤9,0≤c≤5,0≤d≤9,其中a、b、c、d均为整数),则当s为“凸月数”,且s最大时F(s)的值为 .
三.解答题(共11小题,满分84分)
13.(6分)计算:
(1)x2 x3+x7÷x2;
(2).
14.(6分)已知:5a=3,5b=9.
(1)求52a的值;
(2)求55a﹣2b的值.
15.(6分)计算:(x﹣y)(x﹣2y)+(x﹣2y)(x﹣3y)﹣2(x﹣3y)(x﹣4y).
16.(6分)计算:
(1)(x+2﹣3y)(x﹣2+3y);
(2)20212﹣2020×2022(运用整式乘法公式).
17.(6分)已知(x+y)2=49,xy=2,求:
(1)2x2+2y2的值;
(2)(x﹣y)2﹣xy的值.
18.(8分)因式分解:
(1)2x2﹣6x;
(2)4x2﹣y2;
(3)25m2﹣10mn+n2;
(4)12a2b(x﹣y)﹣4ab(y﹣x).
19.(8分)把下列各式因式分解:
(1)﹣3ab3+6a2b2﹣3a3b;
(2)x2﹣y2﹣ax+ay.
20.(8分)【阅读理解,自主探究】把代数式通过配凑等手段,得到完全平方式,再运用完全平方式是非负数这一性质增加问题的条件,这种解题方法叫做配方法,配方法在代数式求值、解方程、最值问题等都有着广泛的应用.
例1:因式分解:a2+6a+8.
解:原式=a2+6a+9﹣1=(a+3)2﹣1=(a+3﹣1)(a+3+1)=(a+2)(a+4).
例2:若M=a2﹣2ab+2b2﹣2b+2,利用配方法求M的最小值.
解:a2﹣2ab+2b2﹣2b+2=a2﹣2ab+b2+b2﹣2b+1+1=(a﹣b)2+(b﹣1)2+1.
∵(a﹣b)2≥0,(b﹣1)2≥0,
∴当a=b=1时,M有最小值1.
请根据上述阅读材料,解决下列问题:
(1)用配方法因式分解:a2﹣12a+35= ;
(2)若M=a2﹣3a+1,则M的最小值为 ;
(3)已知a2+2b2+c2﹣2ab+4b﹣6c+13=0,求a+b+c的值.
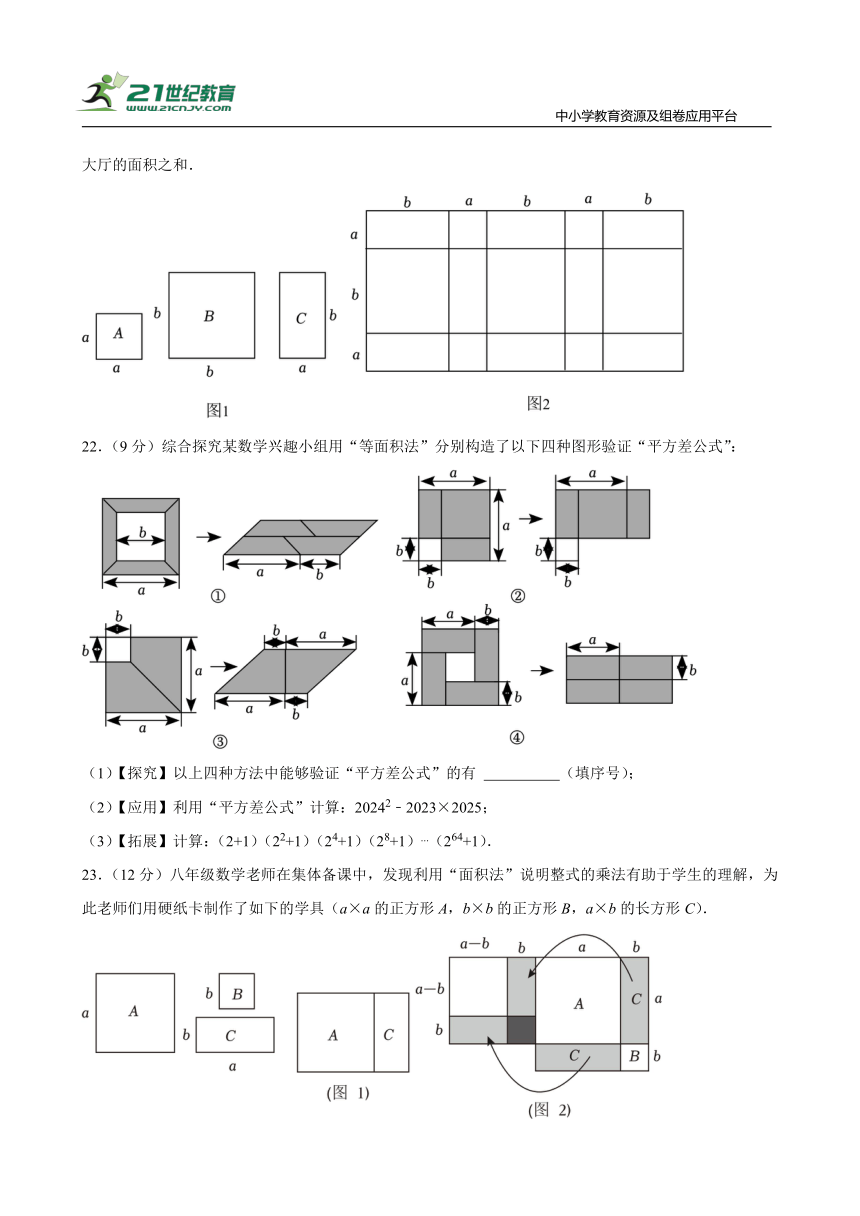
21.(9分)如图1,某商家准备装修商铺,购买了足够多的A(边长为a的小正方形),B(边长为b的大正方形),C(长为b,宽为a的长方形)三种类型的瓷砖来铺设操作间、储藏间和大厅.
(1)操作间刚好按如图2的方式铺满,请求出操作间的面积S(用含a,b的代数式表示);
(2)请通过计算说明:铺满长为(3a+b),宽为(a+2b)的储藏间和长为(4a+3b),宽为(2a+3b)的大厅共需要A,B,C三类瓷砖各多少块?(瓷砖均用整块,无空隙无重叠);
(3)若一块C类瓷砖的周长为32,一块B类瓷砖和一块A类瓷砖的面积之差为64,求操作间、储藏间和大厅的面积之和.
22.(9分)综合探究某数学兴趣小组用“等面积法”分别构造了以下四种图形验证“平方差公式”:
(1)【探究】以上四种方法中能够验证“平方差公式”的有 (填序号);
(2)【应用】利用“平方差公式”计算:20242﹣2023×2025;
(3)【拓展】计算:(2+1)(22+1)(24+1)(28+1) (264+1).
23.(12分)八年级数学老师在集体备课中,发现利用“面积法”说明整式的乘法有助于学生的理解,为此老师们用硬纸卡制作了如下的学具(a×a的正方形A,b×b的正方形B,a×b的长方形C).
(1)在一节课的探究中,小高老师利用1张A和1张C拼出如图1所示的长方形,利用“面积法”可以得出的整式乘法关系式为 ;
(2)在随后的探究中,小高老师在上课时则给同学们发了很多硬纸片(a×a的正方形A,b×b的正方形B,a×b的长方形C),并要求同学们用2张A,1张B和3张C拼成一个长方形,请你在框1中画出对应的示意图,并将利用面积法得出的整式乘法关系式补充完整;
框1
( )( )=2a2+3ab+b2
(3)小朱老师在设计本单元的阶梯作业时,给出如图2所示的示意图,请结合图例,在横线上添加适当的式子,使等式成立;
+ =2a2+2b2
(4)小威老师在培优群中布置了一道思考题:已知(a+b)2+(a﹣b)2=40,求2a+b的最大值,请认真思考,并完成解答.
整式的乘法与因式分解 单元训练(二)
一.选择题(共6小题,满分18分,每小题3分)
1.(3分)下列运算正确的是( )
A.x2+x3=x5 B.(x2)3=x6
C.x4 x3=x12 D.4x2 y2=(4xy)2
【思路点拔】A.先根据同类项的定义判断x2,x3是不是同类项,能否合并即可;
B.根据幂的乘方法则进行计算,然后判断即可;
C.根据同底数幂相乘法则进行计算,然后判断即可;
D.根据逆用积的乘方法则进行计算,然后判断即可.
【解答】解:A.∵x2,x3不是同类项,不能合并,∴此选项的计算错误,故此选项不符合题意;
B.∵(x2)3=x6,∴此选项的计算正确,故此选项符合题意;
C.∵x4 x3=x7,∴此选项的计算错误,故此选项不符合题意;
D.∵4x2 y2=(2xy)2,∴此选项的计算错误,故此选项不符合题意;
故选:B.
2.(3分)计算:(14a3b2﹣7ab2)÷7ab2的结果是( )
A.2a2 B.2a2﹣1 C.2a2﹣b D.2a2b﹣1
【思路点拔】先去括号,再合并同类项即可.
【解答】解:(14a3b2﹣7ab2)÷7ab2
=14a3b2÷7ab2﹣7ab2÷7ab2
=2a2﹣1.
故选:B.
3.(3分)若(x﹣1)(x+2)=ax2+bx+c,则代数式a+b+c的值为( )
A.2 B.0 C.﹣2 D.﹣4
【思路点拔】根据多项式乘多项式的计算法则得到(x﹣1)(x+2)=x2+x﹣2,据此得到a=1,b=1,c=﹣2,再代值计算即可.
【解答】解:∵(x﹣1)(x+2)
=x2﹣x+2x﹣2
=x2+x﹣2,
又∵(x﹣1)(x+2)=ax2+bx+c,
∴x2+x﹣2=ax2+bx+c,
∴a=1,b=1,c=﹣2,
∴a+b+c=1+1﹣2=2﹣2=0,
故选:B.
4.(3分)若a﹣b=8,a2+b2=82,则2ab的值为( )
A.9 B.﹣9 C.18 D.﹣18
【思路点拔】根据完全平方公式进行变形即可求解.
【解答】解:∵a﹣b=8,a2+b2=82,
∴(a﹣b)2=64,
∴a2+b2﹣2ab=64,
∴82﹣2ab=64,
∴2ab=82﹣64=18.
故选:C.
5.(3分)如图①,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形(如图②),通过计算两个图形的面积,验证了一个等式,则这个等式是( )
A.(a+2b)(a﹣b)=a2+ab﹣2b2
B.a2﹣b2=(a+b)(a﹣b)
C.(a﹣b)2=a2﹣2ab+b2
D.(a+b)2=a2+2ab+b2
【思路点拔】根据图①中阴影部分的面积和图②的面积,可以列出等式,从而可以解答本题.
【解答】解:由题意可得,
图①中阴影部分的面积是:a2﹣b2,
图②中矩形的面积是:(a+b)(a﹣b),
∴a2﹣b2=(a+b)(a﹣b),
故选:B.
6.(3分)下列等式中,哪些从左到右的变形是因式分解( )
A.(x+y)(x﹣2y)=x2﹣xy﹣2y2
B.
C.3x2﹣5x﹣2=(3x+1)(x﹣2)
D.3x2+6x+4=3(x+1)2+1
【思路点拔】根据因式分解的定义“将多项式化为几个整式的积的形式”,由此即可求解.
【解答】解:A.(x+y)(x﹣2y)=x2﹣xy﹣2y2,是整数的乘法,不是因式分解,不符合题意;
B.该式子等号右边不几个整式的积的形式,不是因式分解,不符合题意;
C.3x2﹣5x﹣2=(3x+1)(x﹣2),是因式分解,符合题意;
D.3x2+6x+4=3(x+1)2+1,等号右边不几个整式的积的形式,不是因式分解,不符合题意;
故选:C.
二.填空题(共6小题,满分18分,每小题3分)
7.(3分)比较大小:2m+n+1 ≤ 4m+4n.
【思路点拔】令2m=a,2n=b,则2m+n+1=2×2m×2n=2ab,4m+4n=(2m)2+(2n)2=a2+b2,再作差比较大小.
【解答】解:令2m=a,2n=b,则有:
2m+n+1=2×2m×2n=2ab,
4m+4n=(2m)2+(2n)2=a2+b2,
∵a2+b2﹣2ab=(a﹣b)2≥0,仅当a=b,即m=n时取等号,
∴2m+n+1﹣4m+4n≤0,
∴2m+n+1≤4m+4n.
故答案为:≤.
8.(3分)已知4x=2y﹣1,3y+1=27x﹣2,则x﹣y= ﹣9 .
【思路点拔】根据幂的乘方法则化为底数相同的式子,根据指数相等求出x和y的值,即可求出答案.
【解答】解:∵4x=2y﹣1,3y+1=27x﹣2,
∴22x=2y﹣1,3y+1=33x﹣6,
∴2x=y﹣1,y+1=3x﹣6,
∴x=8,y=17,
∴x﹣y=8﹣17=﹣9.
故答案为:﹣9.
9.(3分)计算: 3 .
【思路点拔】根据幂的乘方与积的乘方法则计算即可.
【解答】解:原式=(3)2024×3
=1×3
=3.
故答案为:3.
10.(3分)在横线上填入适当的整式:
(1)(﹣3x2+2y2)( ﹣3x2﹣2y2 )=9x4﹣4y4;
(2)a2+3ab+b2+ ﹣5ab =(a﹣b)2.
【思路点拔】(1)根据平方差公式,进而得出答案;
(2)根据完全平方公式,进而得出答案.
【解答】解:(1)(﹣3x2+2y2)(﹣3x2﹣2y2)=9x4﹣4y4.
故答案为:(﹣3x2﹣2y2).
(2)a2+3ab+b2+(﹣5ab)
=a2﹣2ab+b2
=(a﹣b)2.
故答案为:﹣5ab.
11.(3分)如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个长方形(不重叠无缝隙),则长方形的面积为 (6a+15) cm2.
【思路点拔】分析题意,先求边长为(a+4)的大正方形的面积;再求边长为(a+1)的小正方形的面积;然后用大正方形的面积减去小正方形的面积计算即可.
【解答】解:根据题意得矩形的面积为:
(a+4)2﹣(a+1)2
=(a2+8a+16)﹣(a2+2a+1)
=a2+8a+16﹣a2﹣2a﹣1
=(6a+15)cm2.
故答案为:(6a+15).
12.(3分)若对于一个四位正整数,其千位数字的2倍和百位数字之和为14,十位数字的2倍和个位数字的3倍之和为15,则称这样的四位数为“凸月数”.把任意四位数A的前两位上的数字和后两位上的数字整体交换,得到新四位数A′,规定F(A).则F(6233)的值为 29 .若s=2640+1000a+100b+10c+d(0≤a≤6,3<b≤9,0≤c≤5,0≤d≤9,其中a、b、c、d均为整数),则当s为“凸月数”,且s最大时F(s)的值为 9 .
【思路点拔】(1)根据新定义进行解答;
(2)当4≤b≤7时,根据新定义分别列出方程进行解答求得s,并求得s最大时,F(s)的值.
【解答】解:(1)∵6×2+2=14,3×2+3×3=15,
∴6233是“凸月数”.
∴F(6233)29.
故答案为:29.
(2)当4≤b≤7时,
∵s=2640+1000a+100b+10c+d为“凸月数”,
∴2(a+3)+(b﹣4)=14,2(c+4)+3d=15.
即2a+b=12,2c+3d=7,
∵0≤a≤6,4≤b≤7,0≤c≤5,0≤d≤9,其中a、b、c、d均为整数,
∴a=3,b=6(或a=4,b=4);c=2,d=1.
∴s=6261或7061.
故满足条件s的值为6261或7061.
当s=7061时,F(s)9.
即当s最大时F(s)的值为9.
故答案为:9.
三.解答题(共11小题,满分84分)
13.(6分)计算:
(1)x2 x3+x7÷x2;
(2).
【思路点拔】(1)先根据同底数幂的乘法运算法则和同底数幂的除法运算法则进行计算,然后合并同类项即可;
(2)根据单项式乘多项式的运算法则计算即可.
【解答】解:(1)x2 x3+x7÷x2
=x2+3+x7﹣2
=x5+x5
=2x5;
(2)
1
=8x2y﹣x2+2x.
14.(6分)已知:5a=3,5b=9.
(1)求52a的值;
(2)求55a﹣2b的值.
【思路点拔】(1)根据幂的乘方,底数不变,指数相乘将原式变形为(5a)2,再代入计算即可;
(2)根据同底数幂相除,底数不变,指数相减将原式变形为55a÷52b,再根据幂的乘方法则变形为(5a)5÷(5b)2,最后代入计算即可.
【解答】解:(1)∵5a=3,
∴52a=(5a)2=32=9;
(2)∵5a=3,5b=9,
∴55a﹣2b
=55a÷52b
=(5a)5÷(5b)2
=35÷92
=243÷81
=3.
15.(6分)计算:(x﹣y)(x﹣2y)+(x﹣2y)(x﹣3y)﹣2(x﹣3y)(x﹣4y).
【思路点拔】先根据多项式乘多项式法则计算乘法,然后利用乘法分配律去掉括号,再合并同类项即可.
【解答】解:原式=x2﹣2xy﹣xy+2y2+x2﹣3xy﹣2xy+6y2﹣2(x2﹣4xy﹣3xy+12y2)
=x2﹣3xy+2y2+x2﹣5xy+6y2﹣2(x2﹣7xy+12y2)
=2x2﹣8xy+8y2﹣2x2+14xy﹣24y2
=6xy﹣16y2.
16.(6分)计算:
(1)(x+2﹣3y)(x﹣2+3y);
(2)20212﹣2020×2022(运用整式乘法公式).
【思路点拔】(1)将原式变形为[x+(2﹣3y)][x﹣(2﹣3y)],再利用平方差公式计算;
(2)将原式变形为20212﹣(2021+1)×(2021﹣1),再利用平方差公式计算.
【解答】解:(1)(x+2﹣3y)(x﹣2+3y)
=[x+(2﹣3y)][x﹣(2﹣3y)]
=x2﹣(2﹣3y)2
=x2﹣(4﹣12y+9y2)
=x2﹣9y2+12y﹣4;
(2)20212﹣2020×2022
=20212﹣(2021+1)×(2021﹣1)
=20212﹣20212+1
=1.
17.(6分)已知(x+y)2=49,xy=2,求:
(1)2x2+2y2的值;
(2)(x﹣y)2﹣xy的值.
【思路点拔】(1)把2x2+2y2变形为2(x+y)2﹣4xy,然后整体代入即可求解;
(2)把原式变形为(x+y)2﹣5xy,然后整体代入即可求解.
【解答】解:(1)2x2+2y2
=2(x2+y2)
=2(2xy+x2+y2)﹣4xy
=2(x+y)2﹣4xy
=2×49﹣4×2
=98﹣8
=90;
(2)(x﹣y)2﹣xy
=x2+y2﹣3xy
=x2+y2+2xy﹣5xy
=(x+y)2﹣5xy
=72﹣5×2
=49﹣10
=39.
18.(8分)因式分解:
(1)2x2﹣6x;
(2)4x2﹣y2;
(3)25m2﹣10mn+n2;
(4)12a2b(x﹣y)﹣4ab(y﹣x).
【思路点拔】(1)原式提取公因式2x,分解即可;
(2)利用平方差公式分解即可;
(3)利用完全平方公式分解即可;
(4)原式变形后,提取公因式(x﹣y),再利用平方差公式分解即可.
【解答】解:(1)2x2﹣6x
=2x(x﹣3);
(2)4x2﹣y2
=(2x+y)(2x﹣y);
(3)25m2﹣10mn+n2
=(5m﹣n)2;
(4)12a2b(x﹣y)+4ab(x﹣y)
=4ab(x﹣y)(3a+1).
19.(8分)把下列各式因式分解:
(1)﹣3ab3+6a2b2﹣3a3b;
(2)x2﹣y2﹣ax+ay.
【思路点拔】(1)先提取公因式﹣3ab ,然后利用完全平方公式进行因式分解;
(2)首先分组,进而利用公式法分解因式得出即可.
【解答】解:(1)原式=﹣3ab(b2﹣2ab +a2 )
=﹣3ab(b﹣a)2;
(2)原式=(x2﹣y2)+(﹣ax+ay)
=(x+y)(x﹣y)﹣a(x﹣y)
=(x﹣y)(x+y﹣a).
20.(8分)【阅读理解,自主探究】把代数式通过配凑等手段,得到完全平方式,再运用完全平方式是非负数这一性质增加问题的条件,这种解题方法叫做配方法,配方法在代数式求值、解方程、最值问题等都有着广泛的应用.
例1:因式分解:a2+6a+8.
解:原式=a2+6a+9﹣1=(a+3)2﹣1=(a+3﹣1)(a+3+1)=(a+2)(a+4).
例2:若M=a2﹣2ab+2b2﹣2b+2,利用配方法求M的最小值.
解:a2﹣2ab+2b2﹣2b+2=a2﹣2ab+b2+b2﹣2b+1+1=(a﹣b)2+(b﹣1)2+1.
∵(a﹣b)2≥0,(b﹣1)2≥0,
∴当a=b=1时,M有最小值1.
请根据上述阅读材料,解决下列问题:
(1)用配方法因式分解:a2﹣12a+35= (a﹣7)(a﹣5) ;
(2)若M=a2﹣3a+1,则M的最小值为 ;
(3)已知a2+2b2+c2﹣2ab+4b﹣6c+13=0,求a+b+c的值.
【思路点拔】(1)原式常数项35化为36﹣1,利用完全平方公式化简,再利用平方差公式分求解即可;
(2)M配方后,利用非负数的性质确定出最小值即可;
(3)将已知等式利用完全平方公式配方后,再根据非负数的性质求出a,b,c的值,代入原式计算即可.
【解答】解:(1)a2﹣12a+35
=a2﹣12a+36﹣1
=(a﹣6)2﹣1
=(a﹣7)(a﹣5),
故答案为:(a﹣7)(a﹣5);
(2)M=a2﹣3a+1
M=(a2﹣3a)
M,
当a,即a时,M取最小值,最小值为,
故答案为:;
(3)∵a2+2b2+c2﹣2ab+4b﹣6c+13=0,
∴(a2﹣2ab+b2)+(b2+4b+4)+(c2﹣6c+9)=0,
即 (a﹣b)2+(b+2)2+(c﹣3)2=0,
∵(a﹣b)2≥0,(b+2)2≥0,(c﹣3)2≥0
∴a﹣b=0,b+2=0,c﹣3=0,解得 a=b=﹣2,c=3,
∴a+b+c=﹣2﹣2+3=﹣1.
21.(9分)如图1,某商家准备装修商铺,购买了足够多的A(边长为a的小正方形),B(边长为b的大正方形),C(长为b,宽为a的长方形)三种类型的瓷砖来铺设操作间、储藏间和大厅.
(1)操作间刚好按如图2的方式铺满,请求出操作间的面积S(用含a,b的代数式表示);
(2)请通过计算说明:铺满长为(3a+b),宽为(a+2b)的储藏间和长为(4a+3b),宽为(2a+3b)的大厅共需要A,B,C三类瓷砖各多少块?(瓷砖均用整块,无空隙无重叠);
(3)若一块C类瓷砖的周长为32,一块B类瓷砖和一块A类瓷砖的面积之差为64,求操作间、储藏间和大厅的面积之和.
【思路点拔】(1)观察图形,找出图2的长与宽,利用长方形面积公式,列出算式,利用多项式乘多项式法则进行计算即可;
(2)根据长方形的面积公式,列出算式,利用多项式乘多项式法则求出储藏间和大厅的面积和,根据计算结果求出答案即可;
(3)根据已知条件列出关于a,b的方程组,解方程组求出a,b,然后求出操作间、储藏间和大厅的面积之和,并化简,最后把a,b的值代入化简后的式子,进行计算即可.
【解答】解:(1)由题意得:操作间的长为2a+3b,宽为2a+b,
∴操作间的面积S=(2a+3b)(2a+b)
=4a2+2ab+6ab+3b2
=4a2+8ab+3b2;
(2)由题意得:储藏间和大厅的面积和为:
(3a+b)(a+2b)+(4a+3b)(2a+3b)
=3a2+6ab+ab+2b2+8a2+12ab+6ab+9b2
=11a2+25ab+11b2,
∴共需要A,B各11块,C类瓷砖25块;
(3)由题意可知:2a+2b=32,b2﹣a2=64,
∴a+b=16①,(b+a)(b﹣a)=64,
∴b﹣a=4②,
①+②得:b=10,
把b=10代入①得:a=6
∴操作间、储藏间和大厅的面积之和为:
4a2+8ab+3b2+11a2+25ab+11b2
=4a2+11a2+11b2+3b2+8ab+25ab
=15a2+14b2+33ab
=15×62+14×102+33×10×6
=15×36+14×100+33×10×6
=540+1400+1980
=3920.
22.(9分)综合探究某数学兴趣小组用“等面积法”分别构造了以下四种图形验证“平方差公式”:
(1)【探究】以上四种方法中能够验证“平方差公式”的有 ①②③ (填序号);
(2)【应用】利用“平方差公式”计算:20242﹣2023×2025;
(3)【拓展】计算:(2+1)(22+1)(24+1)(28+1) (264+1).
【思路点拔】(1)用不同的方法分别用代数式表示各个图形中左图、右图阴影部分面积即可得出等式,再进行判断即可;
(2)利用平方差公式进行计算即可;
(3)将原式化为(2﹣1)(2+1)(22+1)(24+1)(28+1) (264+1),再连续利用平方差公式进行计算即可.
【解答】解:(1)图①中,左图阴影部分可以看作两个正方形的面积差,即(a2﹣b2),拼成的右图是底为(a+b),高为(a﹣b)的平行四边形,面积为(a+b)(a﹣b),
∴(a+b)(a﹣b)=a2﹣b2,故图①可以验证平方差公式;
图②中,左图阴影部分可以看作两个正方形的面积差,即(a2﹣b2),拼成的右图是长为(a+b),宽为(a﹣b)的长方形,面积为(a+b)(a﹣b),
∴(a+b)(a﹣b)=a2﹣b2,故图②可以验证平方差公式;
图③中,左图阴影部分可以看作两个正方形的面积差,即(a2﹣b2),拼成的右图是底为(a+b),高为(a﹣b)的平行四边形,面积为(a+b)(a﹣b),
∴(a+b)(a﹣b)=a2﹣b2,故图③可以验证平方差公式;
图④中,左图阴影部分的可以看作两个正方形的面积差,即(a+b)2﹣(a﹣b)2,拼成的右图是长为2a,宽为2b的长方形,面积为4ab,
∴(a+b)2﹣(a﹣b)2=4ab,故图④不能验证平方差公式;
综上所述,能验证平方差公式的有①②③,
故答案为:①②③;
(2)20242﹣2023×2025
=20242﹣(2024﹣1)×(2024+1)
=20242﹣(20242﹣1)
=20242﹣20242+1
=1;
(3)(2+1)(22+1)(24+1)(28+1) (264+1)
=(2﹣1)(2+1)(22+1)(24+1)(28+1) (264+1)
=(22﹣1)(22+1)(24+1)(28+1) (264+1)
=(24﹣1)(24+1)(28+1) (264+1)
=(28﹣1)(28+1) (264+1)
=(216﹣1)(216+1)(232+1)(264+1)
=(232﹣1)(232+1)(264+1)
=(264﹣1)(264+1)
=2128﹣1.
23.(12分)八年级数学老师在集体备课中,发现利用“面积法”说明整式的乘法有助于学生的理解,为此老师们用硬纸卡制作了如下的学具(a×a的正方形A,b×b的正方形B,a×b的长方形C).
(1)在一节课的探究中,小高老师利用1张A和1张C拼出如图1所示的长方形,利用“面积法”可以得出的整式乘法关系式为 a(a+b)=a2+ab ;
(2)在随后的探究中,小高老师在上课时则给同学们发了很多硬纸片(a×a的正方形A,b×b的正方形B,a×b的长方形C),并要求同学们用2张A,1张B和3张C拼成一个长方形,请你在框1中画出对应的示意图,并将利用面积法得出的整式乘法关系式补充完整;
框1
( (a+b) )( (2a+b) )=2a2+3ab+b2
(3)小朱老师在设计本单元的阶梯作业时,给出如图2所示的示意图,请结合图例,在横线上添加适当的式子,使等式成立;
(a﹣b)2 + (a+b)2 =2a2+2b2
(4)小威老师在培优群中布置了一道思考题:已知(a+b)2+(a﹣b)2=40,求2a+b的最大值,请认真思考,并完成解答.
【思路点拔】(1)根据图形用两种方法表示面积即可;
(2)根据(1)种方法画图,并表示面积即可;
(3)根据图形的拼接得到等式即可;
(4)先化简得到a2+b2=20,再设2a+b=m,则b=m﹣2a,代入配方得到5(a)2=20,根据完全平方公式的非负性得到m的取值范围,再确定2a+b的最大值.
【解答】解:(1)根据图示由面积的不同计算方法可得等式:a(a+b)=a2+ab;
故答案为:a(a+b)=a2+ab;
(2)根据题意拼接如下图所示:
根据图示由面积的不同计算方法可得等式:(a+b)(2a+b)=2a2+3ab+b2,
故答案为:(a+b),(2a+b);
(3)根据图示由面积的不同计算方法可得等式:(a﹣b)2+(a+b)2=2a2+2b2,
故答案为:(a﹣b)2,(a+b)2;
(4)∵(a+b)2+(a﹣b)2=40,
∴a2+2ab+b2+a2﹣2ab+b2=40,
整理得:a2+b2=20,
设2a+b=m,则b=m﹣2a,
∴a2+(m﹣2a)2=20,
∴,
∴,
解得:﹣10≤m≤10,
∴2a+b的最大值为10.
整式的乘法与因式分解 单元训练(二)
一.选择题(共6小题,满分18分,每小题3分)
1.(3分)下列运算正确的是( )
A.x2+x3=x5 B.(x2)3=x6
C.x4 x3=x12 D.4x2 y2=(4xy)2
2.(3分)计算:(14a3b2﹣7ab2)÷7ab2的结果是( )
A.2a2 B.2a2﹣1 C.2a2﹣b D.2a2b﹣1
3.(3分)若(x﹣1)(x+2)=ax2+bx+c,则代数式a+b+c的值为( )
A.2 B.0 C.﹣2 D.﹣4
4.(3分)若a﹣b=8,a2+b2=82,则2ab的值为( )
A.9 B.﹣9 C.18 D.﹣18
5.(3分)如图①,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形(如图②),通过计算两个图形的面积,验证了一个等式,则这个等式是( )
A.(a+2b)(a﹣b)=a2+ab﹣2b2
B.a2﹣b2=(a+b)(a﹣b)
C.(a﹣b)2=a2﹣2ab+b2
D.(a+b)2=a2+2ab+b2
6.(3分)下列等式中,哪些从左到右的变形是因式分解( )
A.(x+y)(x﹣2y)=x2﹣xy﹣2y2
B.
C.3x2﹣5x﹣2=(3x+1)(x﹣2)
D.3x2+6x+4=3(x+1)2+1
二.填空题(共6小题,满分18分,每小题3分)
7.(3分)比较大小:2m+n+1 4m+4n.
8.(3分)已知4x=2y﹣1,3y+1=27x﹣2,则x﹣y= .
9.(3分)计算: .
10.(3分)在横线上填入适当的整式:
(1)(﹣3x2+2y2)( )=9x4﹣4y4;
(2)a2+3ab+b2+ =(a﹣b)2.
11.(3分)如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个长方形(不重叠无缝隙),则长方形的面积为 cm2.
12.(3分)若对于一个四位正整数,其千位数字的2倍和百位数字之和为14,十位数字的2倍和个位数字的3倍之和为15,则称这样的四位数为“凸月数”.把任意四位数A的前两位上的数字和后两位上的数字整体交换,得到新四位数A′,规定F(A).则F(6233)的值为 .若s=2640+1000a+100b+10c+d(0≤a≤6,3<b≤9,0≤c≤5,0≤d≤9,其中a、b、c、d均为整数),则当s为“凸月数”,且s最大时F(s)的值为 .
三.解答题(共11小题,满分84分)
13.(6分)计算:
(1)x2 x3+x7÷x2;
(2).
14.(6分)已知:5a=3,5b=9.
(1)求52a的值;
(2)求55a﹣2b的值.
15.(6分)计算:(x﹣y)(x﹣2y)+(x﹣2y)(x﹣3y)﹣2(x﹣3y)(x﹣4y).
16.(6分)计算:
(1)(x+2﹣3y)(x﹣2+3y);
(2)20212﹣2020×2022(运用整式乘法公式).
17.(6分)已知(x+y)2=49,xy=2,求:
(1)2x2+2y2的值;
(2)(x﹣y)2﹣xy的值.
18.(8分)因式分解:
(1)2x2﹣6x;
(2)4x2﹣y2;
(3)25m2﹣10mn+n2;
(4)12a2b(x﹣y)﹣4ab(y﹣x).
19.(8分)把下列各式因式分解:
(1)﹣3ab3+6a2b2﹣3a3b;
(2)x2﹣y2﹣ax+ay.
20.(8分)【阅读理解,自主探究】把代数式通过配凑等手段,得到完全平方式,再运用完全平方式是非负数这一性质增加问题的条件,这种解题方法叫做配方法,配方法在代数式求值、解方程、最值问题等都有着广泛的应用.
例1:因式分解:a2+6a+8.
解:原式=a2+6a+9﹣1=(a+3)2﹣1=(a+3﹣1)(a+3+1)=(a+2)(a+4).
例2:若M=a2﹣2ab+2b2﹣2b+2,利用配方法求M的最小值.
解:a2﹣2ab+2b2﹣2b+2=a2﹣2ab+b2+b2﹣2b+1+1=(a﹣b)2+(b﹣1)2+1.
∵(a﹣b)2≥0,(b﹣1)2≥0,
∴当a=b=1时,M有最小值1.
请根据上述阅读材料,解决下列问题:
(1)用配方法因式分解:a2﹣12a+35= ;
(2)若M=a2﹣3a+1,则M的最小值为 ;
(3)已知a2+2b2+c2﹣2ab+4b﹣6c+13=0,求a+b+c的值.
21.(9分)如图1,某商家准备装修商铺,购买了足够多的A(边长为a的小正方形),B(边长为b的大正方形),C(长为b,宽为a的长方形)三种类型的瓷砖来铺设操作间、储藏间和大厅.
(1)操作间刚好按如图2的方式铺满,请求出操作间的面积S(用含a,b的代数式表示);
(2)请通过计算说明:铺满长为(3a+b),宽为(a+2b)的储藏间和长为(4a+3b),宽为(2a+3b)的大厅共需要A,B,C三类瓷砖各多少块?(瓷砖均用整块,无空隙无重叠);
(3)若一块C类瓷砖的周长为32,一块B类瓷砖和一块A类瓷砖的面积之差为64,求操作间、储藏间和大厅的面积之和.
22.(9分)综合探究某数学兴趣小组用“等面积法”分别构造了以下四种图形验证“平方差公式”:
(1)【探究】以上四种方法中能够验证“平方差公式”的有 (填序号);
(2)【应用】利用“平方差公式”计算:20242﹣2023×2025;
(3)【拓展】计算:(2+1)(22+1)(24+1)(28+1) (264+1).
23.(12分)八年级数学老师在集体备课中,发现利用“面积法”说明整式的乘法有助于学生的理解,为此老师们用硬纸卡制作了如下的学具(a×a的正方形A,b×b的正方形B,a×b的长方形C).
(1)在一节课的探究中,小高老师利用1张A和1张C拼出如图1所示的长方形,利用“面积法”可以得出的整式乘法关系式为 ;
(2)在随后的探究中,小高老师在上课时则给同学们发了很多硬纸片(a×a的正方形A,b×b的正方形B,a×b的长方形C),并要求同学们用2张A,1张B和3张C拼成一个长方形,请你在框1中画出对应的示意图,并将利用面积法得出的整式乘法关系式补充完整;
框1
( )( )=2a2+3ab+b2
(3)小朱老师在设计本单元的阶梯作业时,给出如图2所示的示意图,请结合图例,在横线上添加适当的式子,使等式成立;
+ =2a2+2b2
(4)小威老师在培优群中布置了一道思考题:已知(a+b)2+(a﹣b)2=40,求2a+b的最大值,请认真思考,并完成解答.
整式的乘法与因式分解 单元训练(二)
一.选择题(共6小题,满分18分,每小题3分)
1.(3分)下列运算正确的是( )
A.x2+x3=x5 B.(x2)3=x6
C.x4 x3=x12 D.4x2 y2=(4xy)2
【思路点拔】A.先根据同类项的定义判断x2,x3是不是同类项,能否合并即可;
B.根据幂的乘方法则进行计算,然后判断即可;
C.根据同底数幂相乘法则进行计算,然后判断即可;
D.根据逆用积的乘方法则进行计算,然后判断即可.
【解答】解:A.∵x2,x3不是同类项,不能合并,∴此选项的计算错误,故此选项不符合题意;
B.∵(x2)3=x6,∴此选项的计算正确,故此选项符合题意;
C.∵x4 x3=x7,∴此选项的计算错误,故此选项不符合题意;
D.∵4x2 y2=(2xy)2,∴此选项的计算错误,故此选项不符合题意;
故选:B.
2.(3分)计算:(14a3b2﹣7ab2)÷7ab2的结果是( )
A.2a2 B.2a2﹣1 C.2a2﹣b D.2a2b﹣1
【思路点拔】先去括号,再合并同类项即可.
【解答】解:(14a3b2﹣7ab2)÷7ab2
=14a3b2÷7ab2﹣7ab2÷7ab2
=2a2﹣1.
故选:B.
3.(3分)若(x﹣1)(x+2)=ax2+bx+c,则代数式a+b+c的值为( )
A.2 B.0 C.﹣2 D.﹣4
【思路点拔】根据多项式乘多项式的计算法则得到(x﹣1)(x+2)=x2+x﹣2,据此得到a=1,b=1,c=﹣2,再代值计算即可.
【解答】解:∵(x﹣1)(x+2)
=x2﹣x+2x﹣2
=x2+x﹣2,
又∵(x﹣1)(x+2)=ax2+bx+c,
∴x2+x﹣2=ax2+bx+c,
∴a=1,b=1,c=﹣2,
∴a+b+c=1+1﹣2=2﹣2=0,
故选:B.
4.(3分)若a﹣b=8,a2+b2=82,则2ab的值为( )
A.9 B.﹣9 C.18 D.﹣18
【思路点拔】根据完全平方公式进行变形即可求解.
【解答】解:∵a﹣b=8,a2+b2=82,
∴(a﹣b)2=64,
∴a2+b2﹣2ab=64,
∴82﹣2ab=64,
∴2ab=82﹣64=18.
故选:C.
5.(3分)如图①,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形(如图②),通过计算两个图形的面积,验证了一个等式,则这个等式是( )
A.(a+2b)(a﹣b)=a2+ab﹣2b2
B.a2﹣b2=(a+b)(a﹣b)
C.(a﹣b)2=a2﹣2ab+b2
D.(a+b)2=a2+2ab+b2
【思路点拔】根据图①中阴影部分的面积和图②的面积,可以列出等式,从而可以解答本题.
【解答】解:由题意可得,
图①中阴影部分的面积是:a2﹣b2,
图②中矩形的面积是:(a+b)(a﹣b),
∴a2﹣b2=(a+b)(a﹣b),
故选:B.
6.(3分)下列等式中,哪些从左到右的变形是因式分解( )
A.(x+y)(x﹣2y)=x2﹣xy﹣2y2
B.
C.3x2﹣5x﹣2=(3x+1)(x﹣2)
D.3x2+6x+4=3(x+1)2+1
【思路点拔】根据因式分解的定义“将多项式化为几个整式的积的形式”,由此即可求解.
【解答】解:A.(x+y)(x﹣2y)=x2﹣xy﹣2y2,是整数的乘法,不是因式分解,不符合题意;
B.该式子等号右边不几个整式的积的形式,不是因式分解,不符合题意;
C.3x2﹣5x﹣2=(3x+1)(x﹣2),是因式分解,符合题意;
D.3x2+6x+4=3(x+1)2+1,等号右边不几个整式的积的形式,不是因式分解,不符合题意;
故选:C.
二.填空题(共6小题,满分18分,每小题3分)
7.(3分)比较大小:2m+n+1 ≤ 4m+4n.
【思路点拔】令2m=a,2n=b,则2m+n+1=2×2m×2n=2ab,4m+4n=(2m)2+(2n)2=a2+b2,再作差比较大小.
【解答】解:令2m=a,2n=b,则有:
2m+n+1=2×2m×2n=2ab,
4m+4n=(2m)2+(2n)2=a2+b2,
∵a2+b2﹣2ab=(a﹣b)2≥0,仅当a=b,即m=n时取等号,
∴2m+n+1﹣4m+4n≤0,
∴2m+n+1≤4m+4n.
故答案为:≤.
8.(3分)已知4x=2y﹣1,3y+1=27x﹣2,则x﹣y= ﹣9 .
【思路点拔】根据幂的乘方法则化为底数相同的式子,根据指数相等求出x和y的值,即可求出答案.
【解答】解:∵4x=2y﹣1,3y+1=27x﹣2,
∴22x=2y﹣1,3y+1=33x﹣6,
∴2x=y﹣1,y+1=3x﹣6,
∴x=8,y=17,
∴x﹣y=8﹣17=﹣9.
故答案为:﹣9.
9.(3分)计算: 3 .
【思路点拔】根据幂的乘方与积的乘方法则计算即可.
【解答】解:原式=(3)2024×3
=1×3
=3.
故答案为:3.
10.(3分)在横线上填入适当的整式:
(1)(﹣3x2+2y2)( ﹣3x2﹣2y2 )=9x4﹣4y4;
(2)a2+3ab+b2+ ﹣5ab =(a﹣b)2.
【思路点拔】(1)根据平方差公式,进而得出答案;
(2)根据完全平方公式,进而得出答案.
【解答】解:(1)(﹣3x2+2y2)(﹣3x2﹣2y2)=9x4﹣4y4.
故答案为:(﹣3x2﹣2y2).
(2)a2+3ab+b2+(﹣5ab)
=a2﹣2ab+b2
=(a﹣b)2.
故答案为:﹣5ab.
11.(3分)如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个长方形(不重叠无缝隙),则长方形的面积为 (6a+15) cm2.
【思路点拔】分析题意,先求边长为(a+4)的大正方形的面积;再求边长为(a+1)的小正方形的面积;然后用大正方形的面积减去小正方形的面积计算即可.
【解答】解:根据题意得矩形的面积为:
(a+4)2﹣(a+1)2
=(a2+8a+16)﹣(a2+2a+1)
=a2+8a+16﹣a2﹣2a﹣1
=(6a+15)cm2.
故答案为:(6a+15).
12.(3分)若对于一个四位正整数,其千位数字的2倍和百位数字之和为14,十位数字的2倍和个位数字的3倍之和为15,则称这样的四位数为“凸月数”.把任意四位数A的前两位上的数字和后两位上的数字整体交换,得到新四位数A′,规定F(A).则F(6233)的值为 29 .若s=2640+1000a+100b+10c+d(0≤a≤6,3<b≤9,0≤c≤5,0≤d≤9,其中a、b、c、d均为整数),则当s为“凸月数”,且s最大时F(s)的值为 9 .
【思路点拔】(1)根据新定义进行解答;
(2)当4≤b≤7时,根据新定义分别列出方程进行解答求得s,并求得s最大时,F(s)的值.
【解答】解:(1)∵6×2+2=14,3×2+3×3=15,
∴6233是“凸月数”.
∴F(6233)29.
故答案为:29.
(2)当4≤b≤7时,
∵s=2640+1000a+100b+10c+d为“凸月数”,
∴2(a+3)+(b﹣4)=14,2(c+4)+3d=15.
即2a+b=12,2c+3d=7,
∵0≤a≤6,4≤b≤7,0≤c≤5,0≤d≤9,其中a、b、c、d均为整数,
∴a=3,b=6(或a=4,b=4);c=2,d=1.
∴s=6261或7061.
故满足条件s的值为6261或7061.
当s=7061时,F(s)9.
即当s最大时F(s)的值为9.
故答案为:9.
三.解答题(共11小题,满分84分)
13.(6分)计算:
(1)x2 x3+x7÷x2;
(2).
【思路点拔】(1)先根据同底数幂的乘法运算法则和同底数幂的除法运算法则进行计算,然后合并同类项即可;
(2)根据单项式乘多项式的运算法则计算即可.
【解答】解:(1)x2 x3+x7÷x2
=x2+3+x7﹣2
=x5+x5
=2x5;
(2)
1
=8x2y﹣x2+2x.
14.(6分)已知:5a=3,5b=9.
(1)求52a的值;
(2)求55a﹣2b的值.
【思路点拔】(1)根据幂的乘方,底数不变,指数相乘将原式变形为(5a)2,再代入计算即可;
(2)根据同底数幂相除,底数不变,指数相减将原式变形为55a÷52b,再根据幂的乘方法则变形为(5a)5÷(5b)2,最后代入计算即可.
【解答】解:(1)∵5a=3,
∴52a=(5a)2=32=9;
(2)∵5a=3,5b=9,
∴55a﹣2b
=55a÷52b
=(5a)5÷(5b)2
=35÷92
=243÷81
=3.
15.(6分)计算:(x﹣y)(x﹣2y)+(x﹣2y)(x﹣3y)﹣2(x﹣3y)(x﹣4y).
【思路点拔】先根据多项式乘多项式法则计算乘法,然后利用乘法分配律去掉括号,再合并同类项即可.
【解答】解:原式=x2﹣2xy﹣xy+2y2+x2﹣3xy﹣2xy+6y2﹣2(x2﹣4xy﹣3xy+12y2)
=x2﹣3xy+2y2+x2﹣5xy+6y2﹣2(x2﹣7xy+12y2)
=2x2﹣8xy+8y2﹣2x2+14xy﹣24y2
=6xy﹣16y2.
16.(6分)计算:
(1)(x+2﹣3y)(x﹣2+3y);
(2)20212﹣2020×2022(运用整式乘法公式).
【思路点拔】(1)将原式变形为[x+(2﹣3y)][x﹣(2﹣3y)],再利用平方差公式计算;
(2)将原式变形为20212﹣(2021+1)×(2021﹣1),再利用平方差公式计算.
【解答】解:(1)(x+2﹣3y)(x﹣2+3y)
=[x+(2﹣3y)][x﹣(2﹣3y)]
=x2﹣(2﹣3y)2
=x2﹣(4﹣12y+9y2)
=x2﹣9y2+12y﹣4;
(2)20212﹣2020×2022
=20212﹣(2021+1)×(2021﹣1)
=20212﹣20212+1
=1.
17.(6分)已知(x+y)2=49,xy=2,求:
(1)2x2+2y2的值;
(2)(x﹣y)2﹣xy的值.
【思路点拔】(1)把2x2+2y2变形为2(x+y)2﹣4xy,然后整体代入即可求解;
(2)把原式变形为(x+y)2﹣5xy,然后整体代入即可求解.
【解答】解:(1)2x2+2y2
=2(x2+y2)
=2(2xy+x2+y2)﹣4xy
=2(x+y)2﹣4xy
=2×49﹣4×2
=98﹣8
=90;
(2)(x﹣y)2﹣xy
=x2+y2﹣3xy
=x2+y2+2xy﹣5xy
=(x+y)2﹣5xy
=72﹣5×2
=49﹣10
=39.
18.(8分)因式分解:
(1)2x2﹣6x;
(2)4x2﹣y2;
(3)25m2﹣10mn+n2;
(4)12a2b(x﹣y)﹣4ab(y﹣x).
【思路点拔】(1)原式提取公因式2x,分解即可;
(2)利用平方差公式分解即可;
(3)利用完全平方公式分解即可;
(4)原式变形后,提取公因式(x﹣y),再利用平方差公式分解即可.
【解答】解:(1)2x2﹣6x
=2x(x﹣3);
(2)4x2﹣y2
=(2x+y)(2x﹣y);
(3)25m2﹣10mn+n2
=(5m﹣n)2;
(4)12a2b(x﹣y)+4ab(x﹣y)
=4ab(x﹣y)(3a+1).
19.(8分)把下列各式因式分解:
(1)﹣3ab3+6a2b2﹣3a3b;
(2)x2﹣y2﹣ax+ay.
【思路点拔】(1)先提取公因式﹣3ab ,然后利用完全平方公式进行因式分解;
(2)首先分组,进而利用公式法分解因式得出即可.
【解答】解:(1)原式=﹣3ab(b2﹣2ab +a2 )
=﹣3ab(b﹣a)2;
(2)原式=(x2﹣y2)+(﹣ax+ay)
=(x+y)(x﹣y)﹣a(x﹣y)
=(x﹣y)(x+y﹣a).
20.(8分)【阅读理解,自主探究】把代数式通过配凑等手段,得到完全平方式,再运用完全平方式是非负数这一性质增加问题的条件,这种解题方法叫做配方法,配方法在代数式求值、解方程、最值问题等都有着广泛的应用.
例1:因式分解:a2+6a+8.
解:原式=a2+6a+9﹣1=(a+3)2﹣1=(a+3﹣1)(a+3+1)=(a+2)(a+4).
例2:若M=a2﹣2ab+2b2﹣2b+2,利用配方法求M的最小值.
解:a2﹣2ab+2b2﹣2b+2=a2﹣2ab+b2+b2﹣2b+1+1=(a﹣b)2+(b﹣1)2+1.
∵(a﹣b)2≥0,(b﹣1)2≥0,
∴当a=b=1时,M有最小值1.
请根据上述阅读材料,解决下列问题:
(1)用配方法因式分解:a2﹣12a+35= (a﹣7)(a﹣5) ;
(2)若M=a2﹣3a+1,则M的最小值为 ;
(3)已知a2+2b2+c2﹣2ab+4b﹣6c+13=0,求a+b+c的值.
【思路点拔】(1)原式常数项35化为36﹣1,利用完全平方公式化简,再利用平方差公式分求解即可;
(2)M配方后,利用非负数的性质确定出最小值即可;
(3)将已知等式利用完全平方公式配方后,再根据非负数的性质求出a,b,c的值,代入原式计算即可.
【解答】解:(1)a2﹣12a+35
=a2﹣12a+36﹣1
=(a﹣6)2﹣1
=(a﹣7)(a﹣5),
故答案为:(a﹣7)(a﹣5);
(2)M=a2﹣3a+1
M=(a2﹣3a)
M,
当a,即a时,M取最小值,最小值为,
故答案为:;
(3)∵a2+2b2+c2﹣2ab+4b﹣6c+13=0,
∴(a2﹣2ab+b2)+(b2+4b+4)+(c2﹣6c+9)=0,
即 (a﹣b)2+(b+2)2+(c﹣3)2=0,
∵(a﹣b)2≥0,(b+2)2≥0,(c﹣3)2≥0
∴a﹣b=0,b+2=0,c﹣3=0,解得 a=b=﹣2,c=3,
∴a+b+c=﹣2﹣2+3=﹣1.
21.(9分)如图1,某商家准备装修商铺,购买了足够多的A(边长为a的小正方形),B(边长为b的大正方形),C(长为b,宽为a的长方形)三种类型的瓷砖来铺设操作间、储藏间和大厅.
(1)操作间刚好按如图2的方式铺满,请求出操作间的面积S(用含a,b的代数式表示);
(2)请通过计算说明:铺满长为(3a+b),宽为(a+2b)的储藏间和长为(4a+3b),宽为(2a+3b)的大厅共需要A,B,C三类瓷砖各多少块?(瓷砖均用整块,无空隙无重叠);
(3)若一块C类瓷砖的周长为32,一块B类瓷砖和一块A类瓷砖的面积之差为64,求操作间、储藏间和大厅的面积之和.
【思路点拔】(1)观察图形,找出图2的长与宽,利用长方形面积公式,列出算式,利用多项式乘多项式法则进行计算即可;
(2)根据长方形的面积公式,列出算式,利用多项式乘多项式法则求出储藏间和大厅的面积和,根据计算结果求出答案即可;
(3)根据已知条件列出关于a,b的方程组,解方程组求出a,b,然后求出操作间、储藏间和大厅的面积之和,并化简,最后把a,b的值代入化简后的式子,进行计算即可.
【解答】解:(1)由题意得:操作间的长为2a+3b,宽为2a+b,
∴操作间的面积S=(2a+3b)(2a+b)
=4a2+2ab+6ab+3b2
=4a2+8ab+3b2;
(2)由题意得:储藏间和大厅的面积和为:
(3a+b)(a+2b)+(4a+3b)(2a+3b)
=3a2+6ab+ab+2b2+8a2+12ab+6ab+9b2
=11a2+25ab+11b2,
∴共需要A,B各11块,C类瓷砖25块;
(3)由题意可知:2a+2b=32,b2﹣a2=64,
∴a+b=16①,(b+a)(b﹣a)=64,
∴b﹣a=4②,
①+②得:b=10,
把b=10代入①得:a=6
∴操作间、储藏间和大厅的面积之和为:
4a2+8ab+3b2+11a2+25ab+11b2
=4a2+11a2+11b2+3b2+8ab+25ab
=15a2+14b2+33ab
=15×62+14×102+33×10×6
=15×36+14×100+33×10×6
=540+1400+1980
=3920.
22.(9分)综合探究某数学兴趣小组用“等面积法”分别构造了以下四种图形验证“平方差公式”:
(1)【探究】以上四种方法中能够验证“平方差公式”的有 ①②③ (填序号);
(2)【应用】利用“平方差公式”计算:20242﹣2023×2025;
(3)【拓展】计算:(2+1)(22+1)(24+1)(28+1) (264+1).
【思路点拔】(1)用不同的方法分别用代数式表示各个图形中左图、右图阴影部分面积即可得出等式,再进行判断即可;
(2)利用平方差公式进行计算即可;
(3)将原式化为(2﹣1)(2+1)(22+1)(24+1)(28+1) (264+1),再连续利用平方差公式进行计算即可.
【解答】解:(1)图①中,左图阴影部分可以看作两个正方形的面积差,即(a2﹣b2),拼成的右图是底为(a+b),高为(a﹣b)的平行四边形,面积为(a+b)(a﹣b),
∴(a+b)(a﹣b)=a2﹣b2,故图①可以验证平方差公式;
图②中,左图阴影部分可以看作两个正方形的面积差,即(a2﹣b2),拼成的右图是长为(a+b),宽为(a﹣b)的长方形,面积为(a+b)(a﹣b),
∴(a+b)(a﹣b)=a2﹣b2,故图②可以验证平方差公式;
图③中,左图阴影部分可以看作两个正方形的面积差,即(a2﹣b2),拼成的右图是底为(a+b),高为(a﹣b)的平行四边形,面积为(a+b)(a﹣b),
∴(a+b)(a﹣b)=a2﹣b2,故图③可以验证平方差公式;
图④中,左图阴影部分的可以看作两个正方形的面积差,即(a+b)2﹣(a﹣b)2,拼成的右图是长为2a,宽为2b的长方形,面积为4ab,
∴(a+b)2﹣(a﹣b)2=4ab,故图④不能验证平方差公式;
综上所述,能验证平方差公式的有①②③,
故答案为:①②③;
(2)20242﹣2023×2025
=20242﹣(2024﹣1)×(2024+1)
=20242﹣(20242﹣1)
=20242﹣20242+1
=1;
(3)(2+1)(22+1)(24+1)(28+1) (264+1)
=(2﹣1)(2+1)(22+1)(24+1)(28+1) (264+1)
=(22﹣1)(22+1)(24+1)(28+1) (264+1)
=(24﹣1)(24+1)(28+1) (264+1)
=(28﹣1)(28+1) (264+1)
=(216﹣1)(216+1)(232+1)(264+1)
=(232﹣1)(232+1)(264+1)
=(264﹣1)(264+1)
=2128﹣1.
23.(12分)八年级数学老师在集体备课中,发现利用“面积法”说明整式的乘法有助于学生的理解,为此老师们用硬纸卡制作了如下的学具(a×a的正方形A,b×b的正方形B,a×b的长方形C).
(1)在一节课的探究中,小高老师利用1张A和1张C拼出如图1所示的长方形,利用“面积法”可以得出的整式乘法关系式为 a(a+b)=a2+ab ;
(2)在随后的探究中,小高老师在上课时则给同学们发了很多硬纸片(a×a的正方形A,b×b的正方形B,a×b的长方形C),并要求同学们用2张A,1张B和3张C拼成一个长方形,请你在框1中画出对应的示意图,并将利用面积法得出的整式乘法关系式补充完整;
框1
( (a+b) )( (2a+b) )=2a2+3ab+b2
(3)小朱老师在设计本单元的阶梯作业时,给出如图2所示的示意图,请结合图例,在横线上添加适当的式子,使等式成立;
(a﹣b)2 + (a+b)2 =2a2+2b2
(4)小威老师在培优群中布置了一道思考题:已知(a+b)2+(a﹣b)2=40,求2a+b的最大值,请认真思考,并完成解答.
【思路点拔】(1)根据图形用两种方法表示面积即可;
(2)根据(1)种方法画图,并表示面积即可;
(3)根据图形的拼接得到等式即可;
(4)先化简得到a2+b2=20,再设2a+b=m,则b=m﹣2a,代入配方得到5(a)2=20,根据完全平方公式的非负性得到m的取值范围,再确定2a+b的最大值.
【解答】解:(1)根据图示由面积的不同计算方法可得等式:a(a+b)=a2+ab;
故答案为:a(a+b)=a2+ab;
(2)根据题意拼接如下图所示:
根据图示由面积的不同计算方法可得等式:(a+b)(2a+b)=2a2+3ab+b2,
故答案为:(a+b),(2a+b);
(3)根据图示由面积的不同计算方法可得等式:(a﹣b)2+(a+b)2=2a2+2b2,
故答案为:(a﹣b)2,(a+b)2;
(4)∵(a+b)2+(a﹣b)2=40,
∴a2+2ab+b2+a2﹣2ab+b2=40,
整理得:a2+b2=20,
设2a+b=m,则b=m﹣2a,
∴a2+(m﹣2a)2=20,
∴,
∴,
解得:﹣10≤m≤10,
∴2a+b的最大值为10.
