华师大版数学八年级下册 第18章平行四边形 基础复习(含答案)
文档属性
| 名称 | 华师大版数学八年级下册 第18章平行四边形 基础复习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 854.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-19 00:00:00 | ||
图片预览


文档简介
第18 章平行四边形基础复习
知识点 1 平行四边形的性质
1. 有两组对边分别平行的四边形叫做平行四边形.
2. 平行四边形的性质定理:①定理1:平行四边形的对边相等;②定理2:平行四边形的对角相等;③定理3:平行四边形的对角线互相平分.
3. 平行线之间的距离处处相等.
4. 平行四边形是一个中心对称图形,对角线的交点O就是对称中心.
1. 如图,在 ABCD中,∠B=60°,∠A= ( )
A.120° B.60° C.140° D.30°
2. 平行四边形相邻两边的长分别为24 和16,则平行四边形周长为 ( )
A.20 B.40 C.60 D.80
3. 如图,在平行四边形ABCD中,CE⊥AB于点 E,若∠D=62°,则∠1 的度数为 ( )
A.28° B.38° C.62° D.72°
4. 下列选项中,平行四边形不一定具有的性质是 ( )
A.两组对角分别相等 B.对角线相等
C.对角线互相平分 D.两组对边分别相等
5. 如图,四边形ABCD为平行四边形,作∠BAD 的平分线,交DC 边于点 E,若∠DEA=30°,则∠B的度数为 ( )
A.100° B.120° C.135° D.150°
6. 已知平行四边形的两邻边长为16,20,若两条长边间距离为8,则两条短边间距离为 ( )
A.4 B.5 C.10 D.8
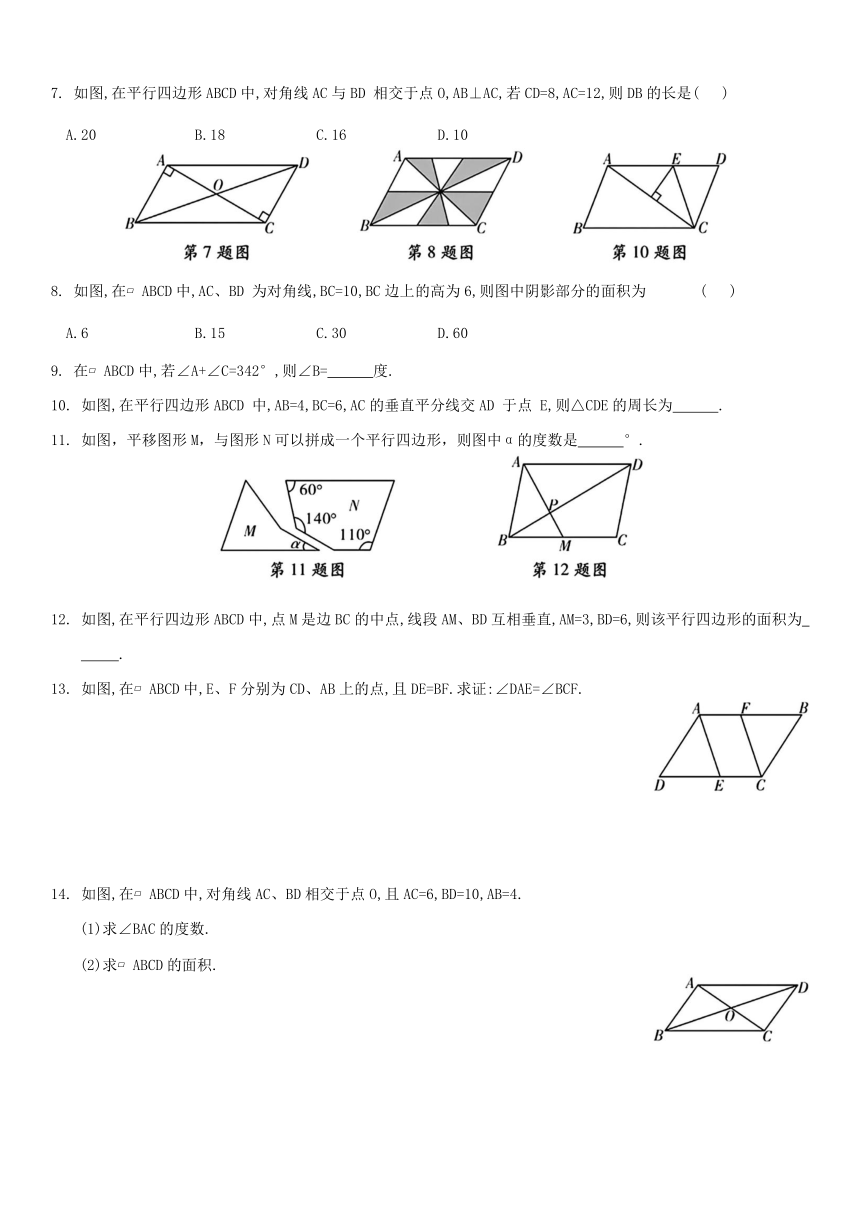
7. 如图,在平行四边形ABCD中,对角线AC与BD 相交于点O,AB⊥AC,若CD=8,AC=12,则DB的长是( )
A.20 B.18 C.16 D.10
8. 如图,在 ABCD中,AC、BD 为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为 ( )
A.6 B.15 C.30 D.60
9. 在 ABCD中,若∠A+∠C=342°,则∠B= 度.
10. 如图,在平行四边形ABCD 中,AB=4,BC=6,AC的垂直平分线交AD 于点 E,则△CDE的周长为 .
11. 如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是 °.
12. 如图,在平行四边形ABCD中,点M是边BC的中点,线段AM、BD互相垂直,AM=3,BD=6,则该平行四边形的面积为 .
13. 如图,在 ABCD中,E、F分别为CD、AB上的点,且DE=BF.求证:∠DAE=∠BCF.
14. 如图,在 ABCD中,对角线AC、BD相交于点O,且AC=6,BD=10,AB=4.
(1)求∠BAC的度数.
(2)求 ABCD的面积.
15. 如图,在平行四边形ABCD中,点 E、F 为对角线AC上的两点,且. ,连结DE、BF.
(1)写出图中所有的全等三角形.
(2)求证:
16. 已知 ,O为对角线AC的中点,过O的一条直线交AD 于点E,交BC于点 F.
(1)求证:
(2)若 的面积为2,求的面积.
知识点 2平行四边形的判定
1. 平行四边形的判定定理1:两组对边分别相等的四边形是平行四边形.
2. 平行四边形的判定定理2:一组对边平行且相等的四边形是平行四边形.
3. 平行四边形的判定定理3:对角线互相平分的四边形是平行四边形.
17. 下面关于平行四边形的说法中,不正确的是 ( )
A.对角线互相平分的四边形是平行四边形
B.有一组对边平行,一组对角相等的四边形是平行四边形
C.有一组对边相等,一组对角相等的四边形是平行四边形
D.有两组对角相等的四边形是平行四边形
18. 在四边形ABCD中,AB=CD,要判定此四边形是平行四边形,还需要满足的条件是 ( )
A.∠A+∠C=180° B.∠B+∠D=180° C.∠A+∠B=180° D.∠A+∠D=180°
19. 学行四边形的相关知识后,小明采用下列方法钉制了一个平行四边形框架:如图,将两根木条AC、BD的中点重叠并用钉子固定,然后用木条将AB、BC、CD、DA 分别钉起来.此时四边形ABCD 即为平行四边形,这样做的依据是 ( )
A.两组对边分别平行的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.对角线互相平分的四边形是平行四边形
20. 在平面直角坐标系中,点O、B、D的坐标分别是(0,0)、(5,0)、(2,3),若存在点C,使得以点O、B、D、C为顶点的四边形是平行四边形,则下列给出的 C 点坐标中,错误的是 ( )
A.(3,-3) B.(-3,3) C.(3,5) D.(7,3)
21. 如图,在平行四边形ABCD 中,E、F分别为AB、DC的中点,则图中共有平行四边形的个数是 ( )
A.3个 B.4个
C.5个 D.6个
22. 若AD=8,AB=4,那么当BC= ,CD= 时,四边形ABCD是平行四边形.
23. 如图,在四边形ABCD中,AD∥BC,AD=12 cm,BC=15 cm,点 P 自点A向D 以1 cm/s的速度运动,到D 点即停止. 点Q 自点 C 向 B 以2cm/s的速度运动,到B点即停止,点P、Q同时出发,设运动时间为t(s).当t= s时,四边形 APQB 是平行四边形.
24. 如图,已知在四边形ABCD中,AD∥BC,点E为CD边上的中点,连结BE并延长,与AD 的延长线交于点 F,连结CF、BD,求证:四边形 DBCF 为平行四边形.
25. 如图,在四边形ABCD中,AB∥CD,且∠D=2∠B.求证:
26. 如图,四边形ABCD中,AC、BD 相交于点 O,延长AD 至点 E,连结EO并延长交CB的延长线于点
(1)求证:O 是线段AC 的中点.
(2)连结AF、EC,求证:四边形AFCE 是平行四边形.
第18章平行四边形基础复习
1. A 2. D 3. A 4. B 5. B 6. C 7. A 8. C 9. 910. 10 11. 20 12. 12
13. 证明:∵ 四边形 ABCD是平行四边形,.
在 和 中,
∴ △ADE≌△CBF(S. A. S.).∴∠DAE=∠BCF.
14. 解:(1)∵ 四边形ABCD 是平行四边形,. ∵AC=6,BD=10,∴AO=3,BO=5.∵AB=4,
是直角三角形,且∠BAC=90°.
(2)∵∠BAC=90°,∴ BA⊥AC.∴ ABCD的面积=AB×AC=4×6=24.
15. (1)解:△ABC≌△CDA,△ABF≌△CDE,△ADE≌△CBF.
[解法提示]
∵四边形ABCD是平行四边形,∴AB=CD,AD=CB,AB∥CD,AD∥CB,∴ ∠BAF = ∠DCE,∠DAE = ∠BCF,在△ABC 和
△CDA 中,
∴△ABC≌△CDA(SSS.).
∵AE=CF,∴AF=CE.
在△ABF 和△CDE中,
∴ △ABF≌△CDE(SAS.).
在△ADE 和△CBF中,
∴ △ADE≌△CBF(SAS.).
(2)证明:∵△ABF≌△CDE,∴∠AFB=∠CED.∴DE∥BF.
16. (1)证明:∵四边形ABCD是平行四边形,∴AD∥BC.
∴∠EAO 是 AC 的中点, 在 和 中,
∴△AOE≌△COF(ASA.).
(2)解:如图,连结 BD,过点 O 作
于点 M.∵ O 为对角线AC 的
中点,∴ O 为AC、BD 的交点.
= 即 的面积为24.
17. C 18. D 19. D 20. C 21. D 22. 8 4 23. 5
24. 证明:
∵E是边 CD的中点,.
在 和 中,
∴ △BEC≌△FED(AAS.).∴BE=FE.∴ 四边形 DBCF 为平行四边形.
25. 证明:如图,过点C作CE∥AD交AB于点E,∵AB∥CD,
∴ 四边形AECD 是平行四边形.
∴AD=CE,CD=AE.
∵AB∥CD,∴∠A+∠D=180°.
∵AD∥CE,∴∠A=∠CEB.
∴∠CEB+∠D=180°.
∵∠D=2∠B,∴∠CEB+2∠B=180°.
∵∠CEB+∠B+∠ECB=180°,
∴∠ECB=∠B.∴EC=EB.∴EB=AD.
∴AB=AE+BE=CD+AD.
26. 证明:(1)∵∠E=∠F,∴AD∥BC.
∵AD=BC,∴四边形ABCD 是平行四边形.
∴AC、BD互相平分.∴O是线段AC的中点.
(2)如图,∵O为线段AC的中点,
∴AO=CO.
在△OAE和△OCF中,
∴△OAE≌△OCF(AAS.).∴OE=OF.
∴ 四边形 AFCE 是平行四边形.
知识点 1 平行四边形的性质
1. 有两组对边分别平行的四边形叫做平行四边形.
2. 平行四边形的性质定理:①定理1:平行四边形的对边相等;②定理2:平行四边形的对角相等;③定理3:平行四边形的对角线互相平分.
3. 平行线之间的距离处处相等.
4. 平行四边形是一个中心对称图形,对角线的交点O就是对称中心.
1. 如图,在 ABCD中,∠B=60°,∠A= ( )
A.120° B.60° C.140° D.30°
2. 平行四边形相邻两边的长分别为24 和16,则平行四边形周长为 ( )
A.20 B.40 C.60 D.80
3. 如图,在平行四边形ABCD中,CE⊥AB于点 E,若∠D=62°,则∠1 的度数为 ( )
A.28° B.38° C.62° D.72°
4. 下列选项中,平行四边形不一定具有的性质是 ( )
A.两组对角分别相等 B.对角线相等
C.对角线互相平分 D.两组对边分别相等
5. 如图,四边形ABCD为平行四边形,作∠BAD 的平分线,交DC 边于点 E,若∠DEA=30°,则∠B的度数为 ( )
A.100° B.120° C.135° D.150°
6. 已知平行四边形的两邻边长为16,20,若两条长边间距离为8,则两条短边间距离为 ( )
A.4 B.5 C.10 D.8
7. 如图,在平行四边形ABCD中,对角线AC与BD 相交于点O,AB⊥AC,若CD=8,AC=12,则DB的长是( )
A.20 B.18 C.16 D.10
8. 如图,在 ABCD中,AC、BD 为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为 ( )
A.6 B.15 C.30 D.60
9. 在 ABCD中,若∠A+∠C=342°,则∠B= 度.
10. 如图,在平行四边形ABCD 中,AB=4,BC=6,AC的垂直平分线交AD 于点 E,则△CDE的周长为 .
11. 如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是 °.
12. 如图,在平行四边形ABCD中,点M是边BC的中点,线段AM、BD互相垂直,AM=3,BD=6,则该平行四边形的面积为 .
13. 如图,在 ABCD中,E、F分别为CD、AB上的点,且DE=BF.求证:∠DAE=∠BCF.
14. 如图,在 ABCD中,对角线AC、BD相交于点O,且AC=6,BD=10,AB=4.
(1)求∠BAC的度数.
(2)求 ABCD的面积.
15. 如图,在平行四边形ABCD中,点 E、F 为对角线AC上的两点,且. ,连结DE、BF.
(1)写出图中所有的全等三角形.
(2)求证:
16. 已知 ,O为对角线AC的中点,过O的一条直线交AD 于点E,交BC于点 F.
(1)求证:
(2)若 的面积为2,求的面积.
知识点 2平行四边形的判定
1. 平行四边形的判定定理1:两组对边分别相等的四边形是平行四边形.
2. 平行四边形的判定定理2:一组对边平行且相等的四边形是平行四边形.
3. 平行四边形的判定定理3:对角线互相平分的四边形是平行四边形.
17. 下面关于平行四边形的说法中,不正确的是 ( )
A.对角线互相平分的四边形是平行四边形
B.有一组对边平行,一组对角相等的四边形是平行四边形
C.有一组对边相等,一组对角相等的四边形是平行四边形
D.有两组对角相等的四边形是平行四边形
18. 在四边形ABCD中,AB=CD,要判定此四边形是平行四边形,还需要满足的条件是 ( )
A.∠A+∠C=180° B.∠B+∠D=180° C.∠A+∠B=180° D.∠A+∠D=180°
19. 学行四边形的相关知识后,小明采用下列方法钉制了一个平行四边形框架:如图,将两根木条AC、BD的中点重叠并用钉子固定,然后用木条将AB、BC、CD、DA 分别钉起来.此时四边形ABCD 即为平行四边形,这样做的依据是 ( )
A.两组对边分别平行的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.对角线互相平分的四边形是平行四边形
20. 在平面直角坐标系中,点O、B、D的坐标分别是(0,0)、(5,0)、(2,3),若存在点C,使得以点O、B、D、C为顶点的四边形是平行四边形,则下列给出的 C 点坐标中,错误的是 ( )
A.(3,-3) B.(-3,3) C.(3,5) D.(7,3)
21. 如图,在平行四边形ABCD 中,E、F分别为AB、DC的中点,则图中共有平行四边形的个数是 ( )
A.3个 B.4个
C.5个 D.6个
22. 若AD=8,AB=4,那么当BC= ,CD= 时,四边形ABCD是平行四边形.
23. 如图,在四边形ABCD中,AD∥BC,AD=12 cm,BC=15 cm,点 P 自点A向D 以1 cm/s的速度运动,到D 点即停止. 点Q 自点 C 向 B 以2cm/s的速度运动,到B点即停止,点P、Q同时出发,设运动时间为t(s).当t= s时,四边形 APQB 是平行四边形.
24. 如图,已知在四边形ABCD中,AD∥BC,点E为CD边上的中点,连结BE并延长,与AD 的延长线交于点 F,连结CF、BD,求证:四边形 DBCF 为平行四边形.
25. 如图,在四边形ABCD中,AB∥CD,且∠D=2∠B.求证:
26. 如图,四边形ABCD中,AC、BD 相交于点 O,延长AD 至点 E,连结EO并延长交CB的延长线于点
(1)求证:O 是线段AC 的中点.
(2)连结AF、EC,求证:四边形AFCE 是平行四边形.
第18章平行四边形基础复习
1. A 2. D 3. A 4. B 5. B 6. C 7. A 8. C 9. 910. 10 11. 20 12. 12
13. 证明:∵ 四边形 ABCD是平行四边形,.
在 和 中,
∴ △ADE≌△CBF(S. A. S.).∴∠DAE=∠BCF.
14. 解:(1)∵ 四边形ABCD 是平行四边形,. ∵AC=6,BD=10,∴AO=3,BO=5.∵AB=4,
是直角三角形,且∠BAC=90°.
(2)∵∠BAC=90°,∴ BA⊥AC.∴ ABCD的面积=AB×AC=4×6=24.
15. (1)解:△ABC≌△CDA,△ABF≌△CDE,△ADE≌△CBF.
[解法提示]
∵四边形ABCD是平行四边形,∴AB=CD,AD=CB,AB∥CD,AD∥CB,∴ ∠BAF = ∠DCE,∠DAE = ∠BCF,在△ABC 和
△CDA 中,
∴△ABC≌△CDA(SSS.).
∵AE=CF,∴AF=CE.
在△ABF 和△CDE中,
∴ △ABF≌△CDE(SAS.).
在△ADE 和△CBF中,
∴ △ADE≌△CBF(SAS.).
(2)证明:∵△ABF≌△CDE,∴∠AFB=∠CED.∴DE∥BF.
16. (1)证明:∵四边形ABCD是平行四边形,∴AD∥BC.
∴∠EAO 是 AC 的中点, 在 和 中,
∴△AOE≌△COF(ASA.).
(2)解:如图,连结 BD,过点 O 作
于点 M.∵ O 为对角线AC 的
中点,∴ O 为AC、BD 的交点.
= 即 的面积为24.
17. C 18. D 19. D 20. C 21. D 22. 8 4 23. 5
24. 证明:
∵E是边 CD的中点,.
在 和 中,
∴ △BEC≌△FED(AAS.).∴BE=FE.∴ 四边形 DBCF 为平行四边形.
25. 证明:如图,过点C作CE∥AD交AB于点E,∵AB∥CD,
∴ 四边形AECD 是平行四边形.
∴AD=CE,CD=AE.
∵AB∥CD,∴∠A+∠D=180°.
∵AD∥CE,∴∠A=∠CEB.
∴∠CEB+∠D=180°.
∵∠D=2∠B,∴∠CEB+2∠B=180°.
∵∠CEB+∠B+∠ECB=180°,
∴∠ECB=∠B.∴EC=EB.∴EB=AD.
∴AB=AE+BE=CD+AD.
26. 证明:(1)∵∠E=∠F,∴AD∥BC.
∵AD=BC,∴四边形ABCD 是平行四边形.
∴AC、BD互相平分.∴O是线段AC的中点.
(2)如图,∵O为线段AC的中点,
∴AO=CO.
在△OAE和△OCF中,
∴△OAE≌△OCF(AAS.).∴OE=OF.
∴ 四边形 AFCE 是平行四边形.
