华师大版数学八年级下册第18章平行四边形 综合测试卷(含答案)
文档属性
| 名称 | 华师大版数学八年级下册第18章平行四边形 综合测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1013.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-19 00:00:00 | ||
图片预览


文档简介
第18章平行四边形综合测试卷
时间:120 分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题3分,共30分)
1. 如图,AB=CD,BC=AD,则下列结论不一定正确的是 ( )
A. AB∥DC B.∠B=∠D C.∠A=∠C D. AB=BC
2. 四边形ABCD 为平行四边形,则∠A:∠B:∠C:∠D 为 ( )
A.1:2:3:4 B.2:3:4:1 C.2:3:2:3 D.2:3:3:2
3. 如图,在平行四边形ABCD中,过点C作CE⊥AB,垂足为E,若∠BAD=127°,则∠BCE的度数为 ( )
A.53° B.37° C.47° D.123°
4. 若 ABCD的周长为30cm,△ABC的周长为24 cm.则AC的长为 ( )
A.6cm B.9 cm C.8cm D.12 cm
5. 已知 ABCD的对角线AC、BD的长分别为12、8,则AB长的范围是 ( )
A. AB>2 B. AB<10 C.26. 小军不慎将一块平行四边形玻璃打碎成如图所示的四块,他带了两块碎玻璃到商店配成了一块与原来相同的平行四边形玻璃,他带的碎玻璃编号是 ( )
A.①② B.①④ C.②③ D.②④
7. 已知四边形ABCD的对角线相交于点O,给出下列4个条件:①AB∥CD;②AB=CD;③OA =OC;④∠BAD=∠BCD.从以上4个条件中任选2个条件为一组,能推出四边形ABCD为平行四边形的有 ( )
A.3组 B.4组 C.5组 D.6组
8. 如图,已知E、F分别为平行四边形ABCD边AD、AB 上的点,则图形中与△BEC 的面积不一定相等的三角形是 ( )
A.△ABD B.△BDC
C.△EFC D.△DCF
9. 如图,在△ABC中,∠ACB=90°,AC=4,AB=5,D为AC上的动点,连结BD,以AD、BD为边作平行四边形ADBE,则DE长的最小值为 ( )
A.2 B.3 C.4 D.5
10. 如图,将 ABCD沿对角线BD折叠,使点A落在点E处,DE交BC于点F,连结CE,则下列结论:①BE=CD;②BF=DF;③S△BEF=S△DCF;④BD∥CE,其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共15分)
11. 如图,在平行四边形ABCD中,E、F两点均在对角线AC上.要使四边形 BEDF 为平行四边形,在不添加辅助线的情况下,需要增加的一个条件是 (写出一个即可).
12. 在探究数学名题“尺规三等分角”的过程中,有下面的问题:如图,BD是平行四边形ABCD 的对角线,点E在BD上,DC=DE=AE,∠1=25°,则∠C的大小是 .
13. 如图,平行四边形ABCD 的顶点C在等边△BEF的边BF上,E点在AB延长线上,G为DE的中点,连结CG,若AD=6,AB=CF=4,则CG的长为 .
14. 如图,点P 是 ABCD内的一点,连结AP、BP、CP、DP,再连结对角线AC,若△APB的面积为20,△APD 的面积为15,那么△APC 的面积为 .
15. 如图,在 ABCD中,已知AD =15 cm,点 P在AD 边上以1 cm/s的速度从点A 向点D 运动,点Q在BC边上以4cm/s的速度从点C 出发在BC 上往返运动,两个点同时出发,当点 P到达点 D 时停止运动(同时Q点也停止),设运动时间为t(s)(t>0),若以P、D、Q、B四点为顶点的四边形是平行四边形,则t的值可以是 .
三、解答题(共75分)
16. (6分)求证:平行四边形的对角线互相平分(要求:根据图形和已知,写出求证和证明过程).已知:在 ABCD中,对角线AC和BD相交于点 E.
求证:
证明:
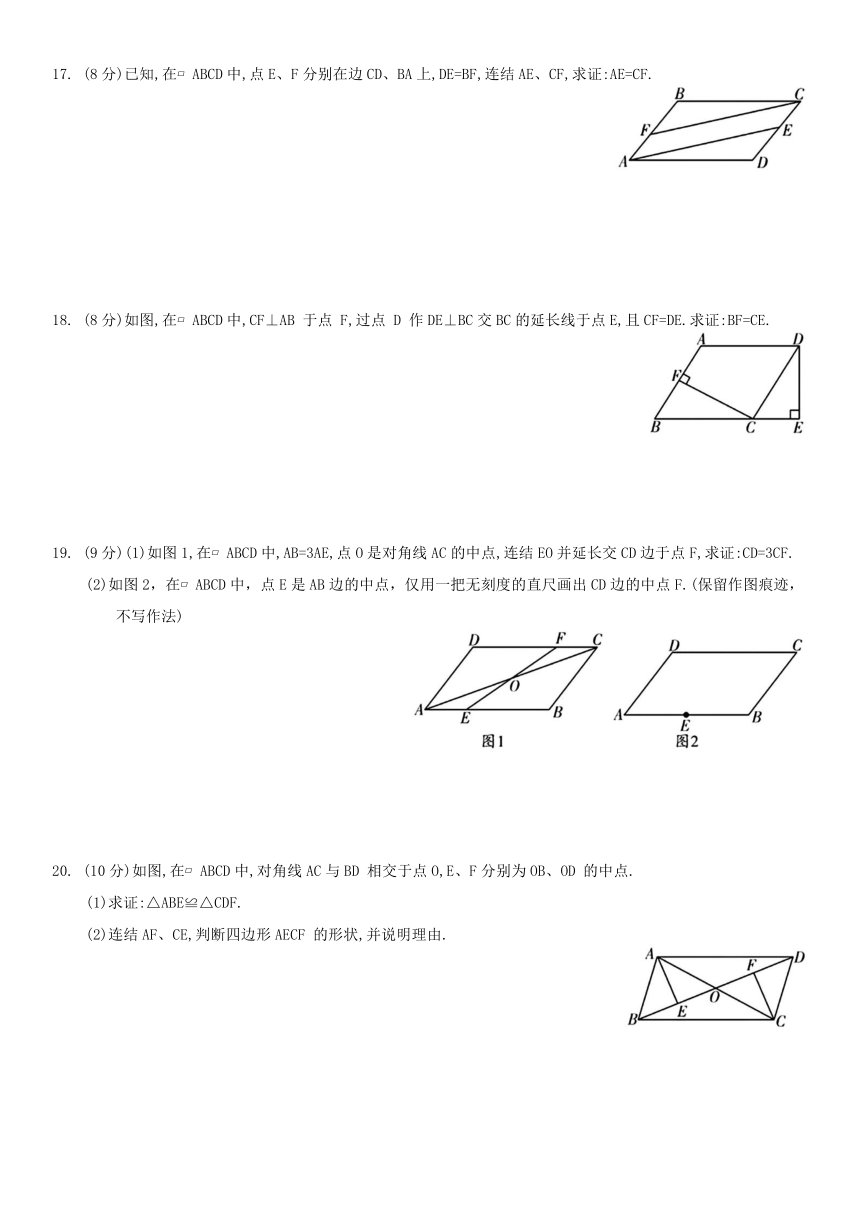
17. (8分)已知,在 ABCD中,点E、F分别在边CD、BA上,DE=BF,连结AE、CF,求证:AE=CF.
18. (8分)如图,在 ABCD中,CF⊥AB 于点 F,过点 D 作DE⊥BC交BC的延长线于点E,且CF=DE.求证:BF=CE.
19. (9分)(1)如图1,在 ABCD中,AB=3AE,点O是对角线AC的中点,连结EO并延长交CD边于点F,求证:CD=3CF.
(2)如图2,在 ABCD中,点E是AB边的中点,仅用一把无刻度的直尺画出CD边的中点F.(保留作图痕迹,不写作法)
20. (10分)如图,在 ABCD中,对角线AC与BD 相交于点O,E、F分别为OB、OD 的中点.
(1)求证:△ABE≌△CDF.
(2)连结AF、CE,判断四边形AECF 的形状,并说明理由.
21. (10分)如图,在平行四边形ABCD中,AC是对角线,且AB=AC,CF是∠ACB的角平分线交AB 于点F,在AD 上取一点E,使AB=AE,连结BE交CF于点 P.
(1)求证:BP=CP.
(2)若BC=4,∠ABC=45°,求平行四边形ABCD 的面积.
22. (12分)如图,在平行四边形ABCD中,E为BC边上的一点,且AB=AE.
(1)求证:△ABC≌△EAD.
(2)若∠AED=70°,求∠ACD 的度数.
(3)若AB=5,BE=6,EC=1,求DE 的长.
23. (12分)若△ABC和△AED 均为等腰三角形,且∠BAC=∠EAD=90°.
(1)如图1,点 B 是DE的中点,判定四边形BEAC的形状,并说明理由.
(2)如图2,若点G是EC的中点,连结GB并延长至点F,使CF=CD.求证:①EB=DC;②∠EBG=∠BFC.
第18章平行四边形综合测试卷
1. D 2. C 3. B 4. B 5. C 6. C 7. A 8. C 9. B 10. D11. AE=CF(答案不唯一) 12. 105° 13. 3 14. 5
15. 6或10 或12
16. 解:求证:EA=EC,EB=ED.
证明:∵ 四边形ABCD 是平行
四边形,∴AD∥BC,AD=BC.
∴∠1 =∠2,
在△AED和△CEB中,
∴△AED≌△CEB(AAS.).∴EA=EC,EB=ED.
17. 证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.
∵DE=BF,∴CE=AF.
∴ 四边形AFCE 是平行四边形.
∴AE=CF.
18. 证明:∵四边形ABCD是平行四边形,∴AB∥CD.
∴ ∠B =∠DCE.又∵CF⊥AB,DE⊥BC,
∴∠BFC=∠E=90°.
在△BCF和△CDE中,
∴△BCF≌△CDE(A. A. S.).∴BF=CE.
19. (1)证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD.
∴∠OAE=∠OCF.∵点O是对角线AC的中点,∴OA=OC.在
△AOE和△COF 中,
∴ △AOE≌△COF(A. S. A.).∴AE=CF.
∵AB=3AE,∴AB=3CF.
又∵AB=CD,∴CD=3CF.
(2)解:如图,连结AC 和 BD 交于点O,连结EO并延长交CD于点 F.点 F 即为CD的中点.
20. (1)证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,
OB=OD.∴∠ABE=∠CDF.∵点E、F分别为OB、OD的中点,
在△ABE 和△CDF
中,
∴△ABE≌△CDF(SAS.).
(2)解:四边形AECF 是平行四边形.理由如下:如图,连结AF、CE,∵四边形ABCD 是平行四边形,∴OA=OC,OB=OD.
∵点E、F分别为OB、OD 的中点,
∴OE=OF.∴四边形AECF 是平行四边形.
21. (1)证明:设AP与BC交于点H,
∵四边形ABCD为平行四边形,∴AD∥BC.
∴∠AEB=∠CBE.
∵AB=AE,∴∠ABE=∠AEB.
∴ ∠ABE=∠CBE.
∴BE平分∠ABC.
∵在△ABC中,CF是∠ACB 的角平分线,BE交CF于点 P,
∴AP平分∠BAC.
∵AB=AC,∴AH⊥BC,且BH=CH.∴AH垂直平分BC.
∴ PB=PC.
(2)解:∵AH⊥BC,∠ABC=45°,∴ BH =AH.∵ BC =4,BH = Cl 平行四边形 ABCD 的面积=BC·AH=4×2=8.
22. (1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.
∴∠AEB=∠EAD.∵AB=AE,∴∠B=∠AEB.∴∠B=∠EAD.
在△ABC和△EAD中,
∴ △ABC≌△EAD(S. A. S.).(2)解:由(1)得△ABC≌△EAD,∴∠BAC=∠AED=70°.
∵ 四边形ABCD 是平行四边形,
∴AB∥DC.∴∠ACD =∠BAC=70°.
(3)解:如图,过点A作AF⊥BC于点 F,
∴ FC=FE+EC=4.在Rt△ABF中,由勾股定理得 在 Rt△AFC中,由勾股定理得 由(1)得
23. (1)解:四边形 BEAC 是平行四边形.理由如下:∵ △AED 为等腰三角形且∠EAD =90°,∴ ∠E =45°.∵ B 是 DE 的中点,∴AB⊥DE.∴∠BAE=45°.∵ △ABC是等腰三角形且∠BAC =90°,∴∠CBA=45°.∴∠BAE=∠CBA.∴BC∥EA.
又∵AB⊥DE,
∴∠EBA=∠BAC=90°.∴BE∥AC.
∴ 四边形 BEAC是平行四边形.
(2)证明:①∵△AED 和△ABC 为等腰三角形,∴AE =AD,AB=AC.∵ ∠EAD =∠BAC =90°,∴ ∠EAD +∠DAB =∠BAC +∠DAB.即∠EAB =∠DAC.∴ △AEB≌△ADC.∴EB=DC.
②如图,延长FG至点H,使GH=FG,连结EH.
∵G是EC中点,∴EG=CG.
又∵∠EGH=∠FGC,
∴△EHG≌△CFG.
∴∠BFC=∠H,CF=EH.
∵CF=CD,BE=CD,∴BE=CF.
∴BE=EH,∴∠EBG=∠H.
∴∠EBG=∠BFC.
时间:120 分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题3分,共30分)
1. 如图,AB=CD,BC=AD,则下列结论不一定正确的是 ( )
A. AB∥DC B.∠B=∠D C.∠A=∠C D. AB=BC
2. 四边形ABCD 为平行四边形,则∠A:∠B:∠C:∠D 为 ( )
A.1:2:3:4 B.2:3:4:1 C.2:3:2:3 D.2:3:3:2
3. 如图,在平行四边形ABCD中,过点C作CE⊥AB,垂足为E,若∠BAD=127°,则∠BCE的度数为 ( )
A.53° B.37° C.47° D.123°
4. 若 ABCD的周长为30cm,△ABC的周长为24 cm.则AC的长为 ( )
A.6cm B.9 cm C.8cm D.12 cm
5. 已知 ABCD的对角线AC、BD的长分别为12、8,则AB长的范围是 ( )
A. AB>2 B. AB<10 C.2
A.①② B.①④ C.②③ D.②④
7. 已知四边形ABCD的对角线相交于点O,给出下列4个条件:①AB∥CD;②AB=CD;③OA =OC;④∠BAD=∠BCD.从以上4个条件中任选2个条件为一组,能推出四边形ABCD为平行四边形的有 ( )
A.3组 B.4组 C.5组 D.6组
8. 如图,已知E、F分别为平行四边形ABCD边AD、AB 上的点,则图形中与△BEC 的面积不一定相等的三角形是 ( )
A.△ABD B.△BDC
C.△EFC D.△DCF
9. 如图,在△ABC中,∠ACB=90°,AC=4,AB=5,D为AC上的动点,连结BD,以AD、BD为边作平行四边形ADBE,则DE长的最小值为 ( )
A.2 B.3 C.4 D.5
10. 如图,将 ABCD沿对角线BD折叠,使点A落在点E处,DE交BC于点F,连结CE,则下列结论:①BE=CD;②BF=DF;③S△BEF=S△DCF;④BD∥CE,其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共15分)
11. 如图,在平行四边形ABCD中,E、F两点均在对角线AC上.要使四边形 BEDF 为平行四边形,在不添加辅助线的情况下,需要增加的一个条件是 (写出一个即可).
12. 在探究数学名题“尺规三等分角”的过程中,有下面的问题:如图,BD是平行四边形ABCD 的对角线,点E在BD上,DC=DE=AE,∠1=25°,则∠C的大小是 .
13. 如图,平行四边形ABCD 的顶点C在等边△BEF的边BF上,E点在AB延长线上,G为DE的中点,连结CG,若AD=6,AB=CF=4,则CG的长为 .
14. 如图,点P 是 ABCD内的一点,连结AP、BP、CP、DP,再连结对角线AC,若△APB的面积为20,△APD 的面积为15,那么△APC 的面积为 .
15. 如图,在 ABCD中,已知AD =15 cm,点 P在AD 边上以1 cm/s的速度从点A 向点D 运动,点Q在BC边上以4cm/s的速度从点C 出发在BC 上往返运动,两个点同时出发,当点 P到达点 D 时停止运动(同时Q点也停止),设运动时间为t(s)(t>0),若以P、D、Q、B四点为顶点的四边形是平行四边形,则t的值可以是 .
三、解答题(共75分)
16. (6分)求证:平行四边形的对角线互相平分(要求:根据图形和已知,写出求证和证明过程).已知:在 ABCD中,对角线AC和BD相交于点 E.
求证:
证明:
17. (8分)已知,在 ABCD中,点E、F分别在边CD、BA上,DE=BF,连结AE、CF,求证:AE=CF.
18. (8分)如图,在 ABCD中,CF⊥AB 于点 F,过点 D 作DE⊥BC交BC的延长线于点E,且CF=DE.求证:BF=CE.
19. (9分)(1)如图1,在 ABCD中,AB=3AE,点O是对角线AC的中点,连结EO并延长交CD边于点F,求证:CD=3CF.
(2)如图2,在 ABCD中,点E是AB边的中点,仅用一把无刻度的直尺画出CD边的中点F.(保留作图痕迹,不写作法)
20. (10分)如图,在 ABCD中,对角线AC与BD 相交于点O,E、F分别为OB、OD 的中点.
(1)求证:△ABE≌△CDF.
(2)连结AF、CE,判断四边形AECF 的形状,并说明理由.
21. (10分)如图,在平行四边形ABCD中,AC是对角线,且AB=AC,CF是∠ACB的角平分线交AB 于点F,在AD 上取一点E,使AB=AE,连结BE交CF于点 P.
(1)求证:BP=CP.
(2)若BC=4,∠ABC=45°,求平行四边形ABCD 的面积.
22. (12分)如图,在平行四边形ABCD中,E为BC边上的一点,且AB=AE.
(1)求证:△ABC≌△EAD.
(2)若∠AED=70°,求∠ACD 的度数.
(3)若AB=5,BE=6,EC=1,求DE 的长.
23. (12分)若△ABC和△AED 均为等腰三角形,且∠BAC=∠EAD=90°.
(1)如图1,点 B 是DE的中点,判定四边形BEAC的形状,并说明理由.
(2)如图2,若点G是EC的中点,连结GB并延长至点F,使CF=CD.求证:①EB=DC;②∠EBG=∠BFC.
第18章平行四边形综合测试卷
1. D 2. C 3. B 4. B 5. C 6. C 7. A 8. C 9. B 10. D11. AE=CF(答案不唯一) 12. 105° 13. 3 14. 5
15. 6或10 或12
16. 解:求证:EA=EC,EB=ED.
证明:∵ 四边形ABCD 是平行
四边形,∴AD∥BC,AD=BC.
∴∠1 =∠2,
在△AED和△CEB中,
∴△AED≌△CEB(AAS.).∴EA=EC,EB=ED.
17. 证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.
∵DE=BF,∴CE=AF.
∴ 四边形AFCE 是平行四边形.
∴AE=CF.
18. 证明:∵四边形ABCD是平行四边形,∴AB∥CD.
∴ ∠B =∠DCE.又∵CF⊥AB,DE⊥BC,
∴∠BFC=∠E=90°.
在△BCF和△CDE中,
∴△BCF≌△CDE(A. A. S.).∴BF=CE.
19. (1)证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD.
∴∠OAE=∠OCF.∵点O是对角线AC的中点,∴OA=OC.在
△AOE和△COF 中,
∴ △AOE≌△COF(A. S. A.).∴AE=CF.
∵AB=3AE,∴AB=3CF.
又∵AB=CD,∴CD=3CF.
(2)解:如图,连结AC 和 BD 交于点O,连结EO并延长交CD于点 F.点 F 即为CD的中点.
20. (1)证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,
OB=OD.∴∠ABE=∠CDF.∵点E、F分别为OB、OD的中点,
在△ABE 和△CDF
中,
∴△ABE≌△CDF(SAS.).
(2)解:四边形AECF 是平行四边形.理由如下:如图,连结AF、CE,∵四边形ABCD 是平行四边形,∴OA=OC,OB=OD.
∵点E、F分别为OB、OD 的中点,
∴OE=OF.∴四边形AECF 是平行四边形.
21. (1)证明:设AP与BC交于点H,
∵四边形ABCD为平行四边形,∴AD∥BC.
∴∠AEB=∠CBE.
∵AB=AE,∴∠ABE=∠AEB.
∴ ∠ABE=∠CBE.
∴BE平分∠ABC.
∵在△ABC中,CF是∠ACB 的角平分线,BE交CF于点 P,
∴AP平分∠BAC.
∵AB=AC,∴AH⊥BC,且BH=CH.∴AH垂直平分BC.
∴ PB=PC.
(2)解:∵AH⊥BC,∠ABC=45°,∴ BH =AH.∵ BC =4,BH = Cl 平行四边形 ABCD 的面积=BC·AH=4×2=8.
22. (1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.
∴∠AEB=∠EAD.∵AB=AE,∴∠B=∠AEB.∴∠B=∠EAD.
在△ABC和△EAD中,
∴ △ABC≌△EAD(S. A. S.).(2)解:由(1)得△ABC≌△EAD,∴∠BAC=∠AED=70°.
∵ 四边形ABCD 是平行四边形,
∴AB∥DC.∴∠ACD =∠BAC=70°.
(3)解:如图,过点A作AF⊥BC于点 F,
∴ FC=FE+EC=4.在Rt△ABF中,由勾股定理得 在 Rt△AFC中,由勾股定理得 由(1)得
23. (1)解:四边形 BEAC 是平行四边形.理由如下:∵ △AED 为等腰三角形且∠EAD =90°,∴ ∠E =45°.∵ B 是 DE 的中点,∴AB⊥DE.∴∠BAE=45°.∵ △ABC是等腰三角形且∠BAC =90°,∴∠CBA=45°.∴∠BAE=∠CBA.∴BC∥EA.
又∵AB⊥DE,
∴∠EBA=∠BAC=90°.∴BE∥AC.
∴ 四边形 BEAC是平行四边形.
(2)证明:①∵△AED 和△ABC 为等腰三角形,∴AE =AD,AB=AC.∵ ∠EAD =∠BAC =90°,∴ ∠EAD +∠DAB =∠BAC +∠DAB.即∠EAB =∠DAC.∴ △AEB≌△ADC.∴EB=DC.
②如图,延长FG至点H,使GH=FG,连结EH.
∵G是EC中点,∴EG=CG.
又∵∠EGH=∠FGC,
∴△EHG≌△CFG.
∴∠BFC=∠H,CF=EH.
∵CF=CD,BE=CD,∴BE=CF.
∴BE=EH,∴∠EBG=∠H.
∴∠EBG=∠BFC.
