华师大版数学八年级下册 第19章矩形,菱形和正方形 基础复习(含答案)
文档属性
| 名称 | 华师大版数学八年级下册 第19章矩形,菱形和正方形 基础复习(含答案) | 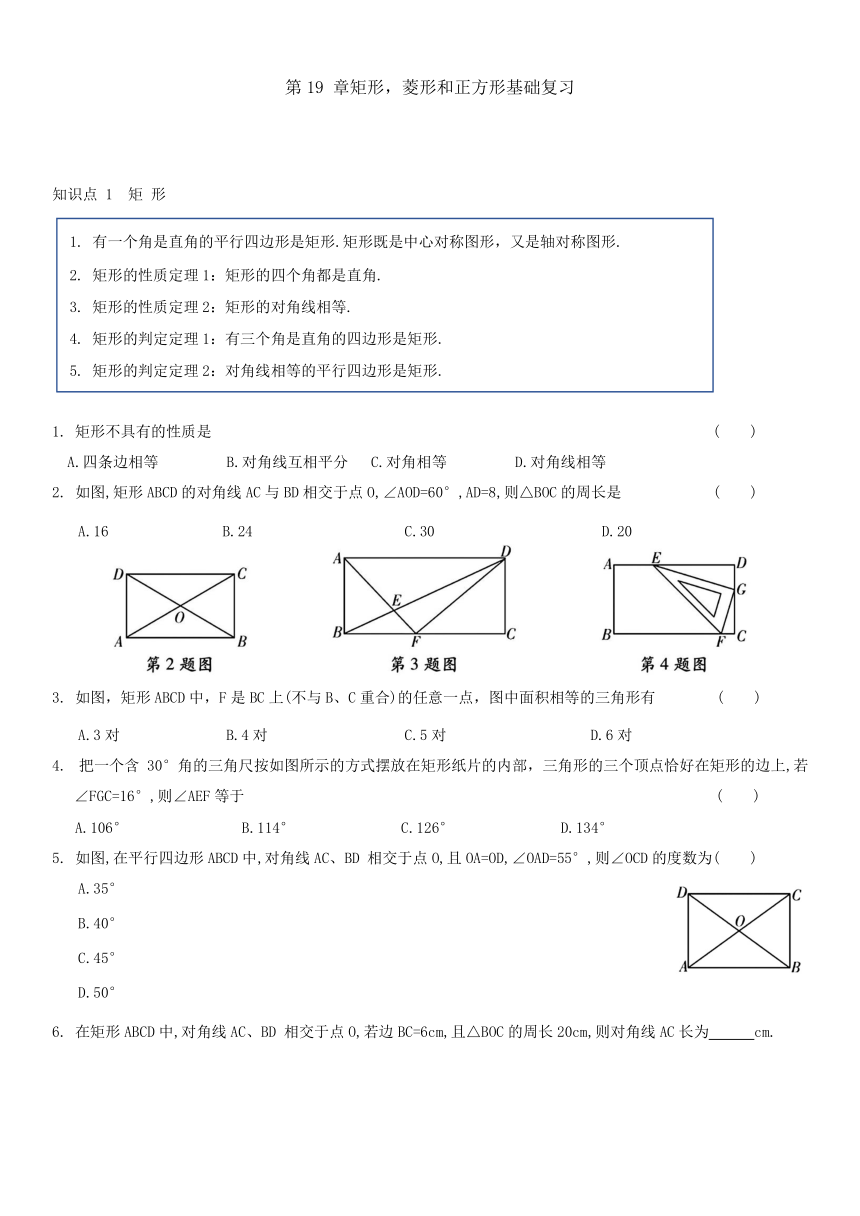 | |
| 格式 | docx | ||
| 文件大小 | 917.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-19 22:49:12 | ||
图片预览


文档简介
第19 章矩形,菱形和正方形基础复习
知识点 1 矩 形
1. 有一个角是直角的平行四边形是矩形.矩形既是中心对称图形,又是轴对称图形.
2. 矩形的性质定理1:矩形的四个角都是直角.
3. 矩形的性质定理2:矩形的对角线相等.
4. 矩形的判定定理1:有三个角是直角的四边形是矩形.
5. 矩形的判定定理2:对角线相等的平行四边形是矩形.
1. 矩形不具有的性质是 ( )
A.四条边相等 B.对角线互相平分 C.对角相等 D.对角线相等
2. 如图,矩形ABCD的对角线AC与BD相交于点O,∠AOD=60°,AD=8,则△BOC的周长是 ( )
A.16 B.24 C.30 D.20
3. 如图,矩形ABCD中,F是BC上(不与B、C重合)的任意一点,图中面积相等的三角形有 ( )
A.3对 B.4对 C.5对 D.6对
4. 把一个含30°角的三角尺按如图所示的方式摆放在矩形纸片的内部,三角形的三个顶点恰好在矩形的边上,若∠FGC=16°,则∠AEF等于 ( )
A.106° B.114° C.126° D.134°
5. 如图,在平行四边形ABCD中,对角线AC、BD 相交于点O,且OA=OD,∠OAD=55°,则∠OCD的度数为( )
A.35°
B.40°
C.45°
D.50°
6. 在矩形ABCD中,对角线AC、BD 相交于点O,若边BC=6cm,且△BOC的周长20cm,则对角线AC长为 cm.
7. 如图,四边形ABCD的对角线互相平分,需要添加一个条件,使它变为矩形,你添加的条件是 .(不要添加任何字母和辅助线)
8. 如图,已知矩形 ABCD,延长 BC 到点 E,连结 DE、DB,若 DB 平分. 且 则
9. 如图,在 中, 将 沿着 BC方向平移得到 ,其中点 E 在边BC上,DE与AC相交于点 O.
(1)求证: 为等腰三角形.
(2)连结AE、DC、AD,当点 E在什么位置时,四边形AECD 为矩形,并说明理由.
10. 如图,点E在矩形ABCD的边CD上,连结AE、BE,过点A 作 于点F,且(
(1)证明:BC=AF.
(2)若∠AEB=2∠CEB,求∠EAF的度数.
知识点 2 菱 形
1. 有一组邻边相等的平行四边形是菱形.菱形既是轴对称图形,也是中心对称图形.
2. 菱形的性质定理1:菱形的四条边都相等.
3. 菱形的性质定理2:菱形的对角形互相垂直.
4. 菱形的面积与两条对角线的关系是:菱形的面积等于两条对角线乘积的一半.
5. 菱形的判定定理1:四条边都相等的四边形是菱形.
6. 菱形的判定定理2:对角线互相垂直的平行四边形是菱形.
11. 若菱形两条对角线的乘积等于48,则这个菱形的面积为 ( )
A.48 B.32 C.24 D.12
12. 如图,菱形ABCD中,∠A=50°,DE⊥AB 于点 E.则∠BDE 的度数为 ( )
A.25° B.35° C.40° D.50°
13. 已知平行四边形ABCD 的对角线相交于点O,补充下列四个条件,能使平行四边形ABCD 成为菱形的是 ( )
A. AB=BD B. AC=BD C.∠DAB=90° D.∠AOB=90°
14. 如图,菱形ABCD的对角线AC、BD交于点O,AC=4,BD=16,将△ABO沿点A到点C的方向平移,得到△A'B'O'.当点A'与点 C重合时,点A 与点B'之间的距离为 ( )
A.6 B.8 C.12 D.10
15. 如图,菱形ABCD中,在边 AD、BC上分别截取 DM=BN,连结 MN交AC 于点O,连结 DO,若∠BAC=20°,则∠ODC 的度数为 ( )
A.20° B.40° C.50° D.70°
16. 如图,在 ABCD中,点E、F分别在边AD、BC上,且DE=BF,则再添加一个条件: 可判定四边形AFCE 是菱形.(只添加一个条件)
17. 如图,在菱形ABCD中,边AB=5,E、F分别在BC和AD上,若 ,且此时. 则BF的长为 .
18. 已知菱形ABCD 的周长为24,对角线AC、BD 交于点O,且 ,则该菱形的面积等于 .
19. 如图,四边形ABCD 是菱形,点 E 是对角线 BD上一点,求证:
20. 四边形ABCD 为平行四边形,AC为对角线,EF垂直平分AC交边AD、BC于点E、F.
(1)如图1,求证:四边形AFCE 是菱形.
(2)如图2,若F是边BC的中点,在不添加任何辅助线的情况下,请直接写出图中与四边形AFCE面积相等的所有三角形和四边形(四边形AFCE 除外).
知识点 3 正方形
1. 正方形既是中心对称图形,又是轴对称图形.
2. 正方形的性质:①四条边都相等;②四个角都是直角;③对角线相等且互相垂直平分.
3. 正方形的判定:①有一个角是直角的菱形是正方形;②有一组邻边相等的矩形是正方形.
21. 如图,四边形ABCD中,AC、BD交于点O,则根据下列条件能判定它是正方形的是 ( )
A.∠DAB=90°且AD=BC B. AB=BC且AC=BD
C.∠DAB=90°且AC⊥BD D. AC⊥BD且AO=BO=CO=DO
22. 如图,正方形ABCD的对角线AC、BD交于点O,P为边 BC上一点,且BP=OB,则∠COP的度数为 ( )
A.15° B.22.5° C.25° D.17.5°
23. 如图,G是边长为4的正方形ABCD边上一点,矩形 DEFG的边EF经过点A,已知GD=5,则FG为 ( )
A.3 B.3.2 C.4 D.4.8
24. 如图,正方形ABCD的边长为4 cm,∠ABE=15°,且AB=AE,则DE= cm.
25. 如图,在矩形ABCD中,AB=6,BC=8.如果E、F分别是AD、BC上的点,G、H是对角线AC上的点.下列判断正确的是 .
①在AC 上存在无数组G、H,使得四边形 EGFH 是平行四边形;
②在AC 上存在无数组G、H,使得四边形EGFH 是矩形;
③在AC 上存在无数组G、H,使得四边形EGFH 是菱形;
④当 时,存在E、F、H,使得四边形 EGFH 是正方形.
26. 如图,已知正方形ABCD,点E是AB上的一点,连结CE,以CE 为一边,在CE的上方作正方形CEFG,连结DG.
求证:(1)△CBE≌△CDG.
(2)AB=AE+DG.
第19章矩形,菱形和正方形基础复习
1. A 2. B 3. C 4. D 5. A 6. 14
(答案不唯一) 8. 5
9. (1)证明:
平移得到
为等腰三角形.
(2)解:如图,当E为BC的中点时,四边形AECD 是矩形.
理由如下:∵AB=AC,E为BC的中点,
∴AE⊥BC,BE=EC.
∵△ABC平移得到△DEF,∴BE∥AD,BE=AD.
∴AD∥EC,AD=EC.∴ 四边形AECD 是平行四边形.
∵AE⊥BC,∴四边形AECD 是矩形.
10. (1)证明:∵四边形ABCD 是矩形,
∴∠C=90°,CD∥AB.
∴ ∠CEB=∠FBA.∵AF⊥BE,∴ ∠AFB =90°.∴ ∠AFB =∠C.
在△BCE 和△AFB中
∴△BCE≌△AFB(A. S. A.).∴BC=AF.
(2)解:∵ 四边形ABCD是矩形,∴∠D=90°,AD=BC.
∵BC=AF,∴AD=AF.∵AF⊥BE,∴∠AFE=90°.
在 Rt△ADE 和 Rt△AFE中,
∴ Rt△ADE≌Rt△AFE(H. L. ).∴ ∠AED =∠AEF.∵ ∠AEB = -90°-72°=18°.
11. C 12. A 13. D 14. D 15. D 16. AE=AF(答案不唯一)17. 18. 28
19. 证明:∵四边形ABCD 是菱形,∴BA=BC,∠ABE=∠CBE.
在△ABE 和△CBE中
∴ △ABE≌△CBE(S. A. S.).∴AE=CE.
20. (1)证明:∵EF垂直平分AC,∴AO=OC,AE=CE,AF=CF.∴∠AEO=∠CEO,∠AFO=∠CFO.又∵ 四边形 ABCD 是平行四边形,∴AD∥BC.∴∠AEO=∠CFO.∴∠AEO=∠AFO,∴AF=AE.∴AE=CE=CF=AF.∴四边形AFCE 是菱形.
(2)解:∵F是边 BC的中点,∴ 四边形AB-CD是平行四边形,∴
由(1)知四边形 AFCE 是菱形,∴ AE = CF,∴ AE = BF. 又∵AD∥BC,∴四边形ABFE 是平行四边形.同理可证:四边形EFCD 是平行四边形.设平行四边形 ABCD 的边 BC 上的高为h.四边形AFCE的面积为S,则S=CF·h,
∵ S四边形ABFE =BF·h=CF·h=S,S四边形EFCD =CF·h=S,S△ABC =
∴图中与四边形AFCE 面积相等的所有三角形和四边形有△ABC,△ADC,四边形ABFE,四边形EFCD.
21. D 22. B 23. B 24. 4 25. ①②③④
26. 证明:(1)∵四边形ABCD 和四边形 CEFG均是正方形,∴CB=CD,CE=CG,∠BCD=∠ECG=90°.∴∠BCE=∠DCG,∴△CBE≌△CDG(S. A. S.).
(2)由(1)知,△CBE≌△CDG,∴BE=DG.∵AB=AE+EB,∴AB=AE+DG.
知识点 1 矩 形
1. 有一个角是直角的平行四边形是矩形.矩形既是中心对称图形,又是轴对称图形.
2. 矩形的性质定理1:矩形的四个角都是直角.
3. 矩形的性质定理2:矩形的对角线相等.
4. 矩形的判定定理1:有三个角是直角的四边形是矩形.
5. 矩形的判定定理2:对角线相等的平行四边形是矩形.
1. 矩形不具有的性质是 ( )
A.四条边相等 B.对角线互相平分 C.对角相等 D.对角线相等
2. 如图,矩形ABCD的对角线AC与BD相交于点O,∠AOD=60°,AD=8,则△BOC的周长是 ( )
A.16 B.24 C.30 D.20
3. 如图,矩形ABCD中,F是BC上(不与B、C重合)的任意一点,图中面积相等的三角形有 ( )
A.3对 B.4对 C.5对 D.6对
4. 把一个含30°角的三角尺按如图所示的方式摆放在矩形纸片的内部,三角形的三个顶点恰好在矩形的边上,若∠FGC=16°,则∠AEF等于 ( )
A.106° B.114° C.126° D.134°
5. 如图,在平行四边形ABCD中,对角线AC、BD 相交于点O,且OA=OD,∠OAD=55°,则∠OCD的度数为( )
A.35°
B.40°
C.45°
D.50°
6. 在矩形ABCD中,对角线AC、BD 相交于点O,若边BC=6cm,且△BOC的周长20cm,则对角线AC长为 cm.
7. 如图,四边形ABCD的对角线互相平分,需要添加一个条件,使它变为矩形,你添加的条件是 .(不要添加任何字母和辅助线)
8. 如图,已知矩形 ABCD,延长 BC 到点 E,连结 DE、DB,若 DB 平分. 且 则
9. 如图,在 中, 将 沿着 BC方向平移得到 ,其中点 E 在边BC上,DE与AC相交于点 O.
(1)求证: 为等腰三角形.
(2)连结AE、DC、AD,当点 E在什么位置时,四边形AECD 为矩形,并说明理由.
10. 如图,点E在矩形ABCD的边CD上,连结AE、BE,过点A 作 于点F,且(
(1)证明:BC=AF.
(2)若∠AEB=2∠CEB,求∠EAF的度数.
知识点 2 菱 形
1. 有一组邻边相等的平行四边形是菱形.菱形既是轴对称图形,也是中心对称图形.
2. 菱形的性质定理1:菱形的四条边都相等.
3. 菱形的性质定理2:菱形的对角形互相垂直.
4. 菱形的面积与两条对角线的关系是:菱形的面积等于两条对角线乘积的一半.
5. 菱形的判定定理1:四条边都相等的四边形是菱形.
6. 菱形的判定定理2:对角线互相垂直的平行四边形是菱形.
11. 若菱形两条对角线的乘积等于48,则这个菱形的面积为 ( )
A.48 B.32 C.24 D.12
12. 如图,菱形ABCD中,∠A=50°,DE⊥AB 于点 E.则∠BDE 的度数为 ( )
A.25° B.35° C.40° D.50°
13. 已知平行四边形ABCD 的对角线相交于点O,补充下列四个条件,能使平行四边形ABCD 成为菱形的是 ( )
A. AB=BD B. AC=BD C.∠DAB=90° D.∠AOB=90°
14. 如图,菱形ABCD的对角线AC、BD交于点O,AC=4,BD=16,将△ABO沿点A到点C的方向平移,得到△A'B'O'.当点A'与点 C重合时,点A 与点B'之间的距离为 ( )
A.6 B.8 C.12 D.10
15. 如图,菱形ABCD中,在边 AD、BC上分别截取 DM=BN,连结 MN交AC 于点O,连结 DO,若∠BAC=20°,则∠ODC 的度数为 ( )
A.20° B.40° C.50° D.70°
16. 如图,在 ABCD中,点E、F分别在边AD、BC上,且DE=BF,则再添加一个条件: 可判定四边形AFCE 是菱形.(只添加一个条件)
17. 如图,在菱形ABCD中,边AB=5,E、F分别在BC和AD上,若 ,且此时. 则BF的长为 .
18. 已知菱形ABCD 的周长为24,对角线AC、BD 交于点O,且 ,则该菱形的面积等于 .
19. 如图,四边形ABCD 是菱形,点 E 是对角线 BD上一点,求证:
20. 四边形ABCD 为平行四边形,AC为对角线,EF垂直平分AC交边AD、BC于点E、F.
(1)如图1,求证:四边形AFCE 是菱形.
(2)如图2,若F是边BC的中点,在不添加任何辅助线的情况下,请直接写出图中与四边形AFCE面积相等的所有三角形和四边形(四边形AFCE 除外).
知识点 3 正方形
1. 正方形既是中心对称图形,又是轴对称图形.
2. 正方形的性质:①四条边都相等;②四个角都是直角;③对角线相等且互相垂直平分.
3. 正方形的判定:①有一个角是直角的菱形是正方形;②有一组邻边相等的矩形是正方形.
21. 如图,四边形ABCD中,AC、BD交于点O,则根据下列条件能判定它是正方形的是 ( )
A.∠DAB=90°且AD=BC B. AB=BC且AC=BD
C.∠DAB=90°且AC⊥BD D. AC⊥BD且AO=BO=CO=DO
22. 如图,正方形ABCD的对角线AC、BD交于点O,P为边 BC上一点,且BP=OB,则∠COP的度数为 ( )
A.15° B.22.5° C.25° D.17.5°
23. 如图,G是边长为4的正方形ABCD边上一点,矩形 DEFG的边EF经过点A,已知GD=5,则FG为 ( )
A.3 B.3.2 C.4 D.4.8
24. 如图,正方形ABCD的边长为4 cm,∠ABE=15°,且AB=AE,则DE= cm.
25. 如图,在矩形ABCD中,AB=6,BC=8.如果E、F分别是AD、BC上的点,G、H是对角线AC上的点.下列判断正确的是 .
①在AC 上存在无数组G、H,使得四边形 EGFH 是平行四边形;
②在AC 上存在无数组G、H,使得四边形EGFH 是矩形;
③在AC 上存在无数组G、H,使得四边形EGFH 是菱形;
④当 时,存在E、F、H,使得四边形 EGFH 是正方形.
26. 如图,已知正方形ABCD,点E是AB上的一点,连结CE,以CE 为一边,在CE的上方作正方形CEFG,连结DG.
求证:(1)△CBE≌△CDG.
(2)AB=AE+DG.
第19章矩形,菱形和正方形基础复习
1. A 2. B 3. C 4. D 5. A 6. 14
(答案不唯一) 8. 5
9. (1)证明:
平移得到
为等腰三角形.
(2)解:如图,当E为BC的中点时,四边形AECD 是矩形.
理由如下:∵AB=AC,E为BC的中点,
∴AE⊥BC,BE=EC.
∵△ABC平移得到△DEF,∴BE∥AD,BE=AD.
∴AD∥EC,AD=EC.∴ 四边形AECD 是平行四边形.
∵AE⊥BC,∴四边形AECD 是矩形.
10. (1)证明:∵四边形ABCD 是矩形,
∴∠C=90°,CD∥AB.
∴ ∠CEB=∠FBA.∵AF⊥BE,∴ ∠AFB =90°.∴ ∠AFB =∠C.
在△BCE 和△AFB中
∴△BCE≌△AFB(A. S. A.).∴BC=AF.
(2)解:∵ 四边形ABCD是矩形,∴∠D=90°,AD=BC.
∵BC=AF,∴AD=AF.∵AF⊥BE,∴∠AFE=90°.
在 Rt△ADE 和 Rt△AFE中,
∴ Rt△ADE≌Rt△AFE(H. L. ).∴ ∠AED =∠AEF.∵ ∠AEB = -90°-72°=18°.
11. C 12. A 13. D 14. D 15. D 16. AE=AF(答案不唯一)17. 18. 28
19. 证明:∵四边形ABCD 是菱形,∴BA=BC,∠ABE=∠CBE.
在△ABE 和△CBE中
∴ △ABE≌△CBE(S. A. S.).∴AE=CE.
20. (1)证明:∵EF垂直平分AC,∴AO=OC,AE=CE,AF=CF.∴∠AEO=∠CEO,∠AFO=∠CFO.又∵ 四边形 ABCD 是平行四边形,∴AD∥BC.∴∠AEO=∠CFO.∴∠AEO=∠AFO,∴AF=AE.∴AE=CE=CF=AF.∴四边形AFCE 是菱形.
(2)解:∵F是边 BC的中点,∴ 四边形AB-CD是平行四边形,∴
由(1)知四边形 AFCE 是菱形,∴ AE = CF,∴ AE = BF. 又∵AD∥BC,∴四边形ABFE 是平行四边形.同理可证:四边形EFCD 是平行四边形.设平行四边形 ABCD 的边 BC 上的高为h.四边形AFCE的面积为S,则S=CF·h,
∵ S四边形ABFE =BF·h=CF·h=S,S四边形EFCD =CF·h=S,S△ABC =
∴图中与四边形AFCE 面积相等的所有三角形和四边形有△ABC,△ADC,四边形ABFE,四边形EFCD.
21. D 22. B 23. B 24. 4 25. ①②③④
26. 证明:(1)∵四边形ABCD 和四边形 CEFG均是正方形,∴CB=CD,CE=CG,∠BCD=∠ECG=90°.∴∠BCE=∠DCG,∴△CBE≌△CDG(S. A. S.).
(2)由(1)知,△CBE≌△CDG,∴BE=DG.∵AB=AE+EB,∴AB=AE+DG.
